离散数学（下）第十章 群与环

1.群的定义（半群、幺半群、群）

要点：
（1）满足可结合 为 半群
（2）满足可结合、单位元、逆元 为 群
2.例子
（1）对于“+”，只有正整数集半群（无单位元），其他如整数加群、有理数加群、实数加群、复数加群都是群
（2）对于n阶矩阵，只有对于矩阵加法才构成群，矩阵乘法只构成独异点（并不是每个矩阵都存在乘法逆元）
（3）对于集合的子集集合，对于对称差⊕运算只构成独异点
3.相关概念

要点：阿贝尔群的二元运算可以交换，即所含的二元运算优先级相同
4.k阶元和无限阶元的定义

5.群的性质
（1）在幂运算的性质中：
<1>(ab)的逆等于b的逆与a的逆的二元运算
<2>在G 为交换群的条件下，(ab)的n次幂等于a的n次幂与b的n次幂的二元运算
（2）满足消去律（对于任意的a,b,c，无限制条件）
（3）

备注：r | k（r整除k，即k是r的整数倍，k%r=0）
（4）

理解：

由上图，可以看出a等于a的逆是由a的2次幂等于单位元推出来的，故存在这个条件时群内只能存在最高二阶元。如果不满足条件的a的2次幂等于单位元，那么也就不满足条件的a等于a的逆，但为了满足a的阶等于a的逆的阶，那么必须让每一个大于2阶的元a都有与它成对出现的逆元，并且这个逆元需满足三个条件：
<1>大于2阶
<2>与a的阶数相同
<3>与a不相等
6.子群的概念

7.子群判定定理（三个）重要！！！



理解：
（1）子群是群的子代数，那么只要证明子代数的基本性质成立即可
（2）子代数有以下基本组成要素：（缺一不可）
<1>封闭性：∀a, b ∈ H，ab ∈ H
相同的代数常数：
<2>e ∈ H
<3>a的逆∈ H

那么其实就可以发现以上三条子群的判定定理都是围绕以上的组成要素去证明其成立性的。
8.生成子群的定义及例子

eg：⟨Z6, ⊕⟩：⟨2⟩ = {0, 2, 4}
9.生成子群相关定理

理解：G为a的生成子群，那么相当于集合内部都为同a类型的元素，不同的在于各元素的阶不同，那么无论怎样交换运算，都不会改变最终的结果
10.中心的定义

要点：可交换元素组成的集合，阿贝尔群的中心即为它自己；对于非交换群而言，中心是{e}
11.共轭子群的定义

12.子群的交

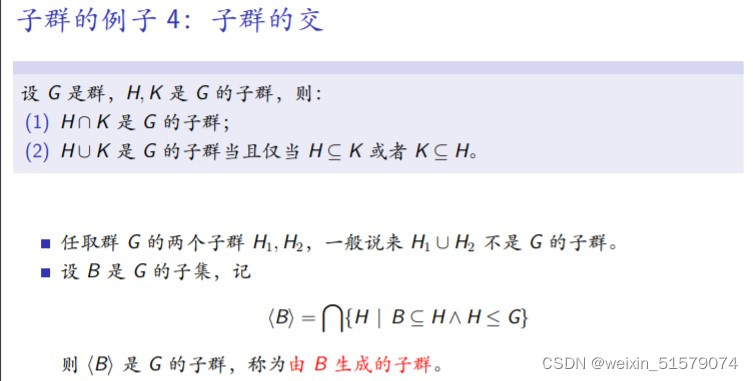
要点：子群的∩能再形成子群，因为交只是缩小了范围，但子群的∪大多数情况下不能再形成子群，因为扩大了集合范围后可能会存在运算不闭合的情况（特例：除非两个子群互为对方的子集，那么这样集合并起来结果就只会是其中的一个子群，那显然符合子群的定义）
13.子群格的定义

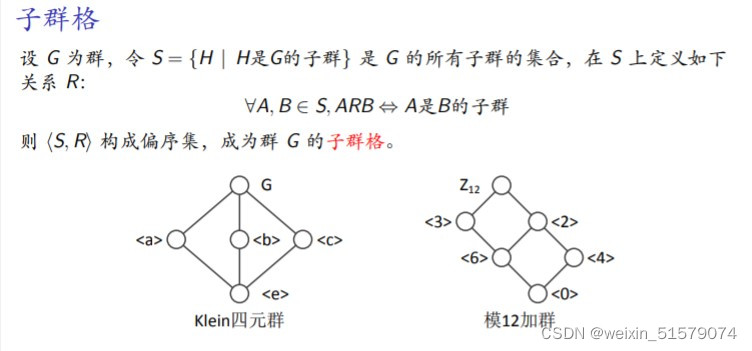
理解：
对于四元群——
⟨e⟩={e} ⟨a⟩={e,a} ⟨b⟩={e,b} ⟨c⟩={e,c} G={e,a,b,c}，根据包含与被包含关系便能画出子群格
14.陪集（左陪集、右陪集）

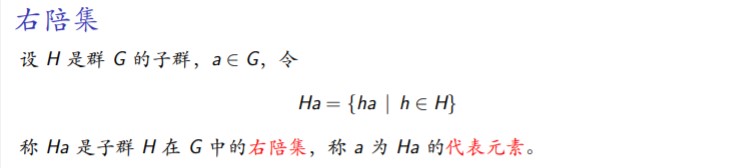
理解：代表元素在哪边，那么就是什么陪集
15.右陪集的性质

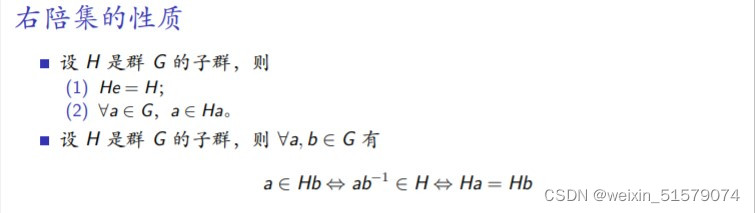
理解：a本应该不属于不包含它的Hb中，但如果属于，则说明a=b

理解：
（1）[a]R表示a的等价类（一种二元关系，满足自反、对称、传递，即a与集合R中的元素有关系，可以理解为<a,b>）
eg：如果b ∈ [a]R，则有<a,b> ∈ R
（2）对于Ha和Hb，只可能存在两种情况，要么a=b，则Ha=Hb;要么a不等于b,那么Ha与Hb交集为空
（3）G 的某一子群的所有右陪集的广义并（合起来）构成G集合本身
（4）约等于说明不完全等于，毕竟陪集会比原来的集合范围更小
16.陪集数：陪集的个数（左陪集数=右陪集数，统称为陪集数）

17.拉格朗日定理 重要！！！

要点：
（1）等式三个元素都是整数
（2）等式的含义：群G的阶等于群H的阶乘以陪集数（|G|表示群中元素的个数）
（3）推论2：如果G是素数阶的群，那么G只由1种元素生成的群
（4）推论3：阶小于6的群都是阿贝尔群（理解：如果是非阿贝尔群，那么集合元素必定不少于6个，e,a,b,ab,ba,aba…）

18.正规子群（不变子群）的定义

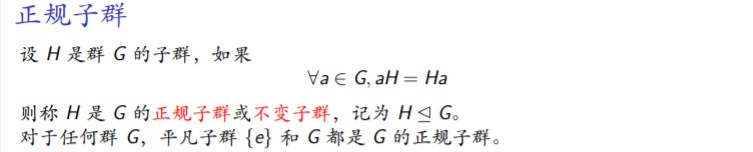
要点：对于H中的任一元素，H的左陪集等于右陪集，那么H为正规子群
理解：
（1）对于只含单位元的群，左右陪集必定相等
（2）对于原来的群G已经包含应包含的所有元素（必须满足封闭性这个基础条件），那么也就满足正规子群的性质
19.单群的定义
如果一个群不存在非平凡的正规子群（只存在平凡的正规子群），则称为单群
20.循环群的定义：生成子群

理解：如果群G是a的生成子群，那么G是循环群
21.循环群的生成元（分为无限循环群和n阶循环群两种情况）

理解：
（1）对于无限循环群，只要有a和a的逆就可以搭建整个群
（2）对于有限循环群，本可以用整个集合表示生成元，但集合中有些幂次无法通过自身简单运算后得到单位元（不适用拉格朗日部分），那么其实只需要将这些与单位元的幂次n互素的幂次对应的元素挑出来作为生成元即可（欧拉函数）
22.循环群的子群

理解：
（1）循环群的性质在子群得到保留
（2）除只含单位元的子群外，其他都是无限子群
（3）拉格朗日定理（一个因子只有一个式子，也就只有一个d阶子群）
23.对称群和置换群的定义

理解：对称群是所有置换群相乘得到的群的统称，对称群包含所有的置换群，置换群是对称群的子群
24.置换的拆分：轮换和对换的定义

要点：
（1）换了k次回到原来就叫做k阶轮换
（2）换了2次回到原来就叫做对换
25.轮换的表示


要点：轮换表示式唯一，但对换表示式不唯一
26.偶置换and奇置换的定义

eg：

27.Polya定理的定义及应用 会用就行

28.环的定义及例子

要点：
（1）“加法”可交换
（2）“乘法”可结合
（3）“乘法”对“加法”满足分配律
eg：（基本都符合环的定义）

29.环的部分性质
（1）x 的加法逆元称为负元，记为 −x；
（2）x 的乘法逆元（如果存在）称为逆元，记为 x的逆
（3）其他性质如单位元与前面所学知识一致
30.环的运算
需要注意的是，在运算的过程中，乘法不满足交换律，加法不满足结合律，加法对乘法不满足分配律，比如ab不等于ba
31.域的定义

要点：（主要针对乘法）
（1）乘法满足交换律——>交换环
（2）乘法存在单位元1——>含幺环
（3）有0参与才等于0——>无零因子环
（4）满足以上三条性质——>整环
（5）在整环的基础上，除0外都有乘法逆元——>域
eg：
（1）Z、Q、R、C都是交换环、含幺环、无零因子环和整环，其中只有Q、R、C是域（Z环并非所有元素都含有乘法逆元）
（2）2Z非幺环和整环，因为1不属于2Z
（3）n阶实矩阵集合Mn®是含幺环，但不是交换环和无零因子环，也不是整环
（4）对于Zn（模n加法和乘法），只有当n为素数时才为域，否则不是无零因子环和整环，因为a⊗b假如等于n，那么结果也会等于0，而不一定需要其中一个乘法因子为零