声学理论基础---梳状滤波效应（二）

Texas king

已于 2024-05-21 16:00:00 修改

阅读量1.3k

点赞数 30

文章标签：音视频音频

于 2024-05-21 15:59:28 首次发布

本文链接：https://blog.csdn.net/qq_39964794/article/details/139095113

版权

音乐和语言信号的梳状滤波作用

图10-3A所示的频谱可以被看成是音乐、语言或者其他信号的瞬间片段。图10-3B 所示是一个与图10-3A所示频谱完全相同的信号，只是相对A信号有着0.1ms 的延时。如果单独来看这两个信号，延时对它们来说没有任何影响，但是当它们叠加在一起，将会产生新的频谱。图10-3C所示是信号A和B在话筒振膜处的叠加频谱。它的频率响应与上面单音信号叠加的结果不同，展示出梳状滤波效应，它有着在频率上的峰值(相长干涉)和谷值(相消干涉)特征。把其绘制在一个频率为线性的刻度上，看起来就像把梳子，因此取名为梳状滤波效应。

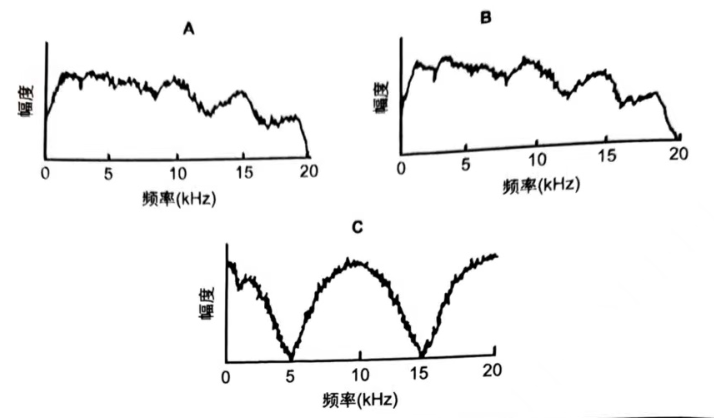
image/png

图10-3梳状滤波信号的频谱分布。(A)音乐信号的瞬态频谱。(B)A信号的复制品，但是它与A之间有0.1ms

的延时。(C)A和C的叠加信号产生了典型的梳状滤波效应。图中频率坐标使用的是线性刻度

直达声和反射声的梳状滤波作用

图10-3 所示0.1ms的延时信号可以来自数字延时设备，又或者来自墙面等其他物体的反射。信号的频谱形状会随着反射声的变化而发生改变，这取决于声音的入射角度以及反射表面的声学特征等。当直达声与反射声进行合并时，将会产生梳状滤波作用，它会在频率响应当中产生典型的结点(也称作波谷 )。当2个信号反相时就会产生结点，它们在时间上相差(1/2)波长。结点(和峰值)的频率取决于直达声和反射声之间的延时时间。第1个结点频率发生在周期是延时时间2倍的位置。可以通过

来表示，其中t为延时时间，用s 来表示。每一个连续的结点，发生在该频率的奇数倍位置，表示为

，其中n=1，3，5，7....。第一个峰值发生在ƒ=1/t的位置，同时连续的峰值发生在ƒ=n/t，其中n=1，2，3，4，5.....。两个相邻结点或者峰值之间的频率间隔为1/t。

具有 0.1ms 延时的反射声将会落后直达声(1130 英尺 / s)( 0.001s )=1.13 英尺。这1.34英寸的路程差，可能是由于声源与听众之间的贴地角(Grazing Angle )，或者话筒附近的反射表面所造成的。如图 10-4所示，大多数延时对频率响应的影响是可以预知的。图10-4A 所示的频谱是无反射环境下由全指向话筒所拾取的随机噪声，该信号是由扬声器发出的。由于这种噪声信号是一种连续且能量在整个可听频率范围分布的信号，故它比正弦或者其他周期波形更加接近语言和音乐信号，从而被广泛应用于声学测量当中。

图10-4B 所示扬声器正对着一个反射表面。话筒放置在距离反射表面约0.7 英寸的位置，在话筒位置，来自扬声器的直达声与来自表面的反射声之间形成了干涉。话筒的输出，显示出0.1ms延时的梳状滤波特征。

我们把话筒放置在距离反射表面 3.4 英寸处，将会产生 0.5ms 的延时，其梳状滤波特征如图10-4C 所示。当延时从0.1ms 增加到 0.5ms 时，峰值和结点的数量已经增加了5倍。如图10-4D所示，话筒与反射表面之间的距离为 6.75 英寸，产生了1ms 的延时。从图中看出，当延时增加1 倍时，其峰值和结点的数量也增加1倍。

增加直达声和反射声之间的延时，相长干涉和相消干涉的数量会成比例增长。从图 10-4A所示的平直频谱开始，到被 0.1ms 的反射延时声所破坏，并形成频谱 B。这种响应的变化是可以被听到的。频谱 D 的改变是很难被察觉的，因为峰值和结点之间的间隔非常近，倾向于对整个畸变进行了平均。

image/png

图10-4一个梳状滤波效应的展示，其中扬声器产生的直达声与墙面的反射声在话筒振膜处叠加在一起。(A)没有反射表面的情况。(B)把话筒放置在距离反射表面0.7 英寸的地方，产生了0.1m 的延时，同时直达声和反射声的叠加显示出在 5KHz和15kHz 处的结点。(C)0.5ms 延时所产生的结点间隔更加紧密。(D)1ms 延时会产生更加紧密的结点间隔。如果延时t是以s 来计量的，那么第1个结点位置在 1/(2t)处，且2个结点之间的间隔或者2个峰值之间的间隔为 1/t。图中频率使用的是线性刻度

我们知道在较小的房间当中，反射声与直达声之间的间隔将会更小，这是由房间尺寸的限制造成的。与此相反，在较大的空间当中，反射声将会有更长的延时，会使梳状滤波作用产生间隔更加紧密的峰值和结点。因此，梳状滤波作用通常与小房间的声学特征有着更加紧密的联系。由于音乐厅及礼堂的尺寸较大，故会对人耳能觉察的梳状滤波失真有着相对较好的免疫作用。如此多且紧密的峰值和结点，可以让响应趋于平直。图 10-5 展示了音乐信号通过 2ms 延时梳状滤波器所产生的频谱。响应的峰值与结点之间的关系，以及其对应的音符如图所示。中央C(C4)的频率为261.63Hz，它接近于第一个结点 250Hz的位置。下一个更高的C(C5)，有着C4两倍的频率，其幅度比C4高 6dB。在钢琴键盘上其他的 C5，其频率响应要么受到结点抵消，要么被峰值提高，又或者在两者之间。无论我们把它们看作基频还是谐波，声音的音色最终都受到了影响。

图10-3、图10-4以及图10-5 展示的梳状滤波响应是在线性频率刻度下完成的。在这种线性关系的刻度下，所产生梳状外观的可视性更加形象。而在电子和音频工业当中对数刻度更为常用，它更能代表人们的听觉感受。如图 10-6 所示，为对数刻度下 1ms 延时的梳状滤波作用。

image/png