- 时间:2021年7月27日
- 论文名称:Cellular Neural Networks: Theory
- 学习内容:学习细胞神经网络理论,基于Tensorflow实现论文的Fig9、Fig12
- 下一步学习计划:学习Matlab,并实现论文的Fig9、Fig12
- 源码地址:https://colab.research.google.com/drive/1suK2aalw7J0iCrfTCPeVHg-qzAj-SNs-?usp=sharing
- 文章目录
1.导入模块
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import matplotlib.ticker as ticker
from scipy.interpolate import make_interp_spline
!gdown --id 1fsKERl26TNTFIY25PhReoCujxwJvfyHn
zhfont = mpl.font_manager.FontProperties(fname='SimHei .ttf')
zhfont2 = mpl.font_manager.FontProperties(fname='New Times Roman .ttf')
2.设置初始状态
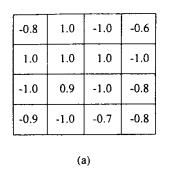
# 设置初始状态
epochs = 7
input_x = tf.constant([
[
[[-0.8],[1.0],[-1.0],[-0.6]],
[[1.0],[1.0],[1.0],[-1.0]],
[[-1.0],[0.9],[-1.0],[-0.8]],
[[-0.9],[-1.0],[-0.7],[-0.8]],
],
],dtype=tf.float32)
print(input_x.shape)
# 设置filters
filters = tf.constant([
[[0.0],[1.0],[0.0]],
[[1.0],[2.0],[1.0]],
[[0.0],[1.0],[0.0]],
],dtype=tf.float32)
print(filters.shape)
bias = tf.constant(0.0,shape=[1])
filterinput = tf.reshape(filters, [3, 3, 1, 1])
print(filterinput.shape)
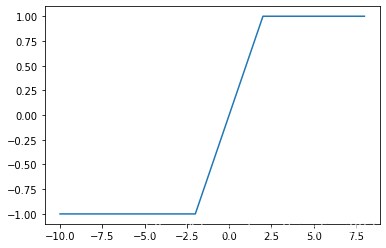
3.输出值的过滤函数
def sign(x):
if x > 1:
return 1
elif x < -1:
return -1
else:
return x
rng = [i for i in range(-10,10,2)]
y = [sign(x) for x in rng]
plt.plot(rng, y)
4.细胞神经网络卷积运算
论文公式:

def func(input_x):
# x1:存储单个细胞的状态值
x1 = []
# y1:存储单个细胞的输出值
x1 = []
y1 = []
A1 = np.zeros([4,4],dtype=float)
A2 = np.zeros([4,4],dtype=float)
# 记录初始状态值值并打印
for i in range(4):
for j in range(4):
A1[i][j] = float(input_x[0][i][j][0])
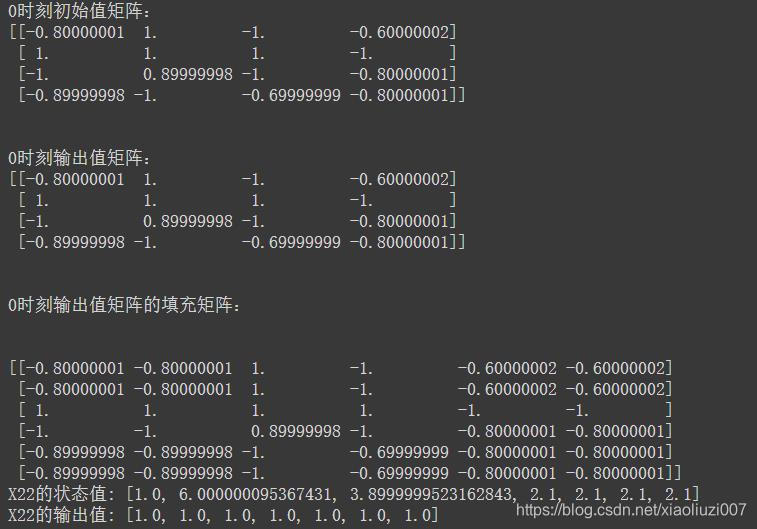
print("0时刻初始值矩阵:")
print(A1)
print('\n')
x1.append(A1[1][1])
# 记录初始输出值并打印
for i in range(4):
for j in range(4):
A2[i][j] = sign(float(input_x[0][i][j][0]))
print("0时刻输出值矩阵:")
print(A2)
print('\n')
y1.append(A2[1][1])
# 记录初始输出值的填充效果并打印
A3 = np.pad(A2, ((1,1), (1,1)), 'edge')
print("0时刻输出值矩阵的填充矩阵:")
print('\n')
print(A3)
for k in range(epochs-1):
input_x = tf.reshape(tf.convert_to_tensor(A3,dtype=tf.float32), [1, 6, 6, 1])
# 卷积运算
input_x = tf.nn.conv2d(input_x, filterinput, strides=[1,1,1,1], padding='VALID')+bias
for i in range(4):
for j in range(4):
A1[i][j] = float(input_x[0][i][j][0]) + A2[i][j]*0.1 #2.2
for i in range(4):
for j in range(4):
A2[i][j] = sign(float(input_x[0][i][j][0]))
x1.append(A1[1][1])
y1.append(A2[1][1])
A3 = np.pad(A2, ((1,1), (1,1)), 'edge')
print('X22的状态值:',x1)
print('X22的输出值:',y1)
return x1,y1
c_x,c_y = func(input_x)
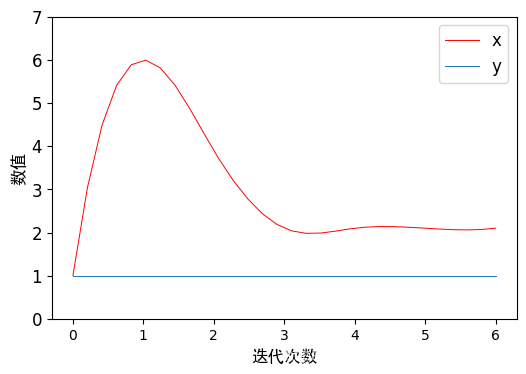
5.数据可视化
# 可视化(拟合曲线)
plt.figure(dpi = 100)
T = np.array(range(epochs))
xnew = np.linspace(T.min(),T.max(),30)
c_x_power_smooth = make_interp_spline(T,c_x)(xnew)
plt.plot(xnew, c_x_power_smooth, label='y',linewidth = '0.7',color = 'red')
plt.plot(T, c_y, label='x', linewidth = '0.7')
plt.xlabel(u"迭代次数",fontproperties=zhfont,fontsize=12)
plt.ylabel(u"数值",fontproperties=zhfont,fontsize=12)
plt.yticks(np.arange(0, epochs+1, 1),fontproperties = 'Times New Roman', size = 12)
plt.legend(fontsize=12)
plt.show()
6.多个初始状态对比分析
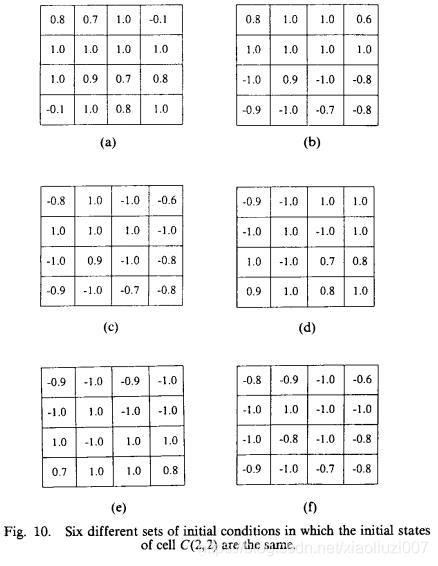
# 设置矩阵初始状态
input_x_a = tf.constant([
[
[[0.8],[0.7],[1.0],[-0.1]],
[[1.0],[1.0],[1.0],[1.0]],
[[1.0],[0.9],[0.7],[0.8]],
[[-0.1],[1.0],[0.8],[1.8]],
],
],dtype=tf.float32)
input_x_b = tf.constant([
[
[[0.8],[1.0],[1.0],[0.6]],
[[1.0],[1.0],[1.0],[1.0]],
[[-1.0],[0.9],[-1.0],[-0.8]],
[[-0.9],[-1.0],[-0.7],[-0.8]],
],
],dtype=tf.float32)
input_x_d = tf.constant([
[
[[-0.9],[-1.0],[1.0],[1.0]],
[[-1.0],[1.0],[-1.0],[1.0]],
[[1.0],[-1.0],[0.7],[0.8]],
[[0.9],[1.0],[0.8],[1.0]],
],
],dtype=tf.float32)
input_x_e = tf.constant([
[
[[-0.9],[-1.0],[-0.9],[-0.1]],
[[-1.0],[1.0],[-1.0],[-1.0]],
[[1.0],[-1.0],[1.0],[1.0]],
[[0.7],[1.0],[1.0],[0.8]],
],
],dtype=tf.float32)
input_x_f = tf.constant([
[
[[-0.8],[-0.9],[-1.0],[-0.6]],
[[-1.0],[1.0],[-1.0],[-1.0]],
[[-1.0],[-0.8],[-1.0],[-0.8]],
[[-0.9],[-1.0],[-0.7],[-0.8]],
],
],dtype=tf.float32)
a_x,a_y = func(input_x_a)
b_x,b_y = func(input_x_b)
d_x,d_y = func(input_x_d)
e_x,e_y = func(input_x_e)
f_x,f_y = func(input_x_f)
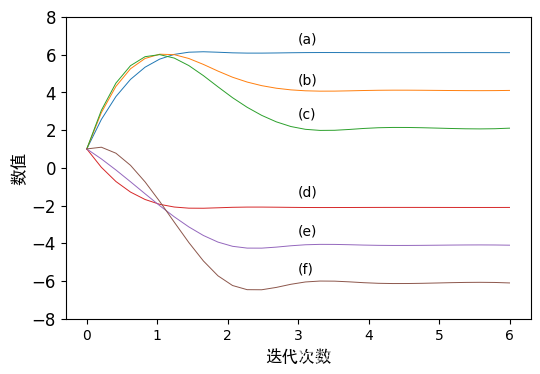
# 可视化(拟合曲线)
plt.figure(dpi = 100)
T = np.array(range(epochs))
xnew = np.linspace(T.min(),T.max(),30)
a_x_power_smooth = make_interp_spline(T,a_x)(xnew)
b_x_power_smooth = make_interp_spline(T,b_x)(xnew)
c_x_power_smooth = make_interp_spline(T,c_x)(xnew)
d_x_power_smooth = make_interp_spline(T,d_x)(xnew)
e_x_power_smooth = make_interp_spline(T,e_x)(xnew)
f_x_power_smooth = make_interp_spline(T,f_x)(xnew)
plt.plot(xnew, a_x_power_smooth, linewidth = '0.7')
plt.plot(xnew, b_x_power_smooth, linewidth = '0.7')
plt.plot(xnew, c_x_power_smooth, linewidth = '0.7')
plt.plot(xnew, d_x_power_smooth, linewidth = '0.7')
plt.plot(xnew, e_x_power_smooth, linewidth = '0.7')
plt.plot(xnew, f_x_power_smooth, linewidth = '0.7')
plt.xlabel(u"迭代次数",fontproperties=zhfont,fontsize=12)
plt.ylabel(u"数值",fontproperties=zhfont,fontsize=12)
plt.yticks(np.arange(-(epochs+1), epochs+2, 2),fontproperties = 'Times New Roman', size = 12)
plt.text(3, 6.6, '(a)')
plt.text(3, 4.4, '(b)')
plt.text(3, 2.6, '(c)')
plt.text(3, -1.5, '(d)')
plt.text(3, -3.6, '(e)')
plt.text(3, -5.6, '(f)')
plt.show()
print("如果文章对你有用,请点个赞呗O(∩_∩)O~")
System.out.println("如果文章对你有用,请点个赞呗O(∩_∩)O~");
cout<<"如果文章对你有用,请点个赞呗O(∩_∩)O~"<<endl;

























 2327
2327











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








