课程1 费马原理与变折射率光学(视频1-4)学习笔记

光学简介与分类：

近代物理起源于光学

---

几何光学三定律、费马原理与相应推导

费马原理是几何光学最高的理论概括·

费马原理可推导出几何三定律、各类透镜反射镜的物像关系。

折射定律

光线经过透明介质 入射角i1，折射角i2，入射介质折射率n1，折射介质折射率n2，则有公式：
$$n_1\ast sin(i_1)=n_2\ast sin(i_2).$$
折射率必然与色散有关，因为不同波长的折射率有差。

惠更斯原理（次波源，微观 次波面）

波前的每一点可以认为是产生球面次波的点波源，而以后任何时刻的波前则可看作是这些次波的包络。

Tip：惠更斯原理在用于 界面的反射、折射时，将赋予折射率的物理意义

$$\frac{n_1}{n_2}=\frac{v_2}{v_1}.$$
由于 波速 = 频率 x 波长，令 n2 = 1，为真空介质。则该公式转化为
$$n=\frac{f_0\ast {\lambda }_0}{f\ast \lambda }.$$

考虑到 在线性介质的光场中，扰动的时间频率f仅由光源决定，与介质无关，最终可得
$$n=\frac{{\lambda }_0}{\lambda }.$$

光程

在相同时间内光在真空中传播的距离。当处于介质中时，即将路程进行折合，为 路程乘以 折射率。变折射率下，为折射率的变积分。

光程的意义：
1、相位差与光程的关系：沿着波的传播方向，位相逐点落后
$$\varphi (P)-\varphi (Q)=-\frac{2\pi }{{\lambda }_0}\ast L(QP).$$
2、时差与光程的关系（c为光速）
$$t_P-t_Q=\frac{L(QP)}{c}.$$

费马原理

光线经过QP两点，虚拟路径有无数条，但实际光纤只走唯一一条QP，即 光线沿光程为平稳值(极小值、极大值、常数值)的路径进行传播。

费马原理 在均匀介质中 为 直线传播定律；在介质界面中 为 反射定律与折射定律。

费马原理推论：物像之间各条光线的光程是相等的-----物像等光程性。

意义：
严格等光程→严格成像；
近似等光程→近似成像；
非等光程→不成像；

三种反射面等光程点：
1、旋转椭圆面；2旋转抛物面；3、旋转双曲面；
以下为3种反射面的等光程点（齐明点）

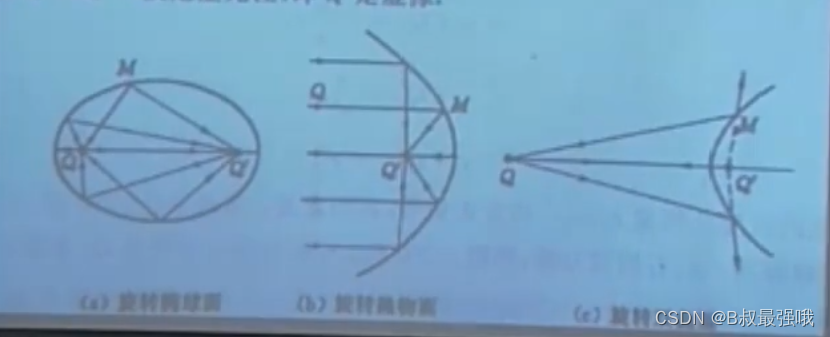
透射面等光程点应用：油镜

阿贝正弦定理

显微镜上存在一个齐明点，满足阿贝正弦定理（近似等光程点），消除了一般轴外小物产生的慧差：
物方折射率 n、小物线度y 、 入射倾角 u ，像方折射率 n‘、小像线度y’ 、 出射倾角 u’ ，该公式又称蔡司公式。
$$n\ast y\ast sinu=n^{\prime }\ast y^{\prime }\ast sin{u}^{\prime }.$$

双曲面透镜下 无穷远点与像点 等光程点

变折射率

变折射率环境：
寒冷海面上空（极光与海市蜃楼）随着高度折射率下降
炽热地面上空（沙洲神泉）随着高度折射率上升

折射率连续变化情况，光线会弯曲，同理声波。
大气电离层，随着高度升高，折射率成抛物型。

人工变折射率材质：
光纤，单极传输

微透镜

非线性光学

在强光条件下，光束被限制于介质棒中传播，发生衍射 ，发生类似凸透镜自聚焦与类似凹透镜自散焦。

强光光学中用于研究强光与晶体介质的相互作用。
信息光学中用于光存储的读出与写入。

变折射率下的光程方程

特殊 n(y) 任意微小弧元，微分线段 ds。
有
$$(ds{)}^2=(dx{)}^2+(dy{)}^2.$$
即
$$(\frac{dy}{dx}{)}^2=(\frac{ds}{dx}{)}^2-1.$$
注意到
$$\frac{ds}{dx}=\frac{1}{sin\theta }$$
根据折射定律可知
$$n(y)\ast sin\theta (y)=n_0\ast sin{\theta }_0$$
则有
$$(dy/dx{)}^2=((n(y)/(n_0\ast sin{\theta }_0){)}^2-1$$
根据初条件，求得 y(x) 的曲线函数。
对上式再次求导可获得
$$\frac{(dy{)}^2}{d{x}^2}=\frac{1}{2n_0^2(sin\theta {)}^2}\ast \frac{dn(y){)}^2}{dy}$$

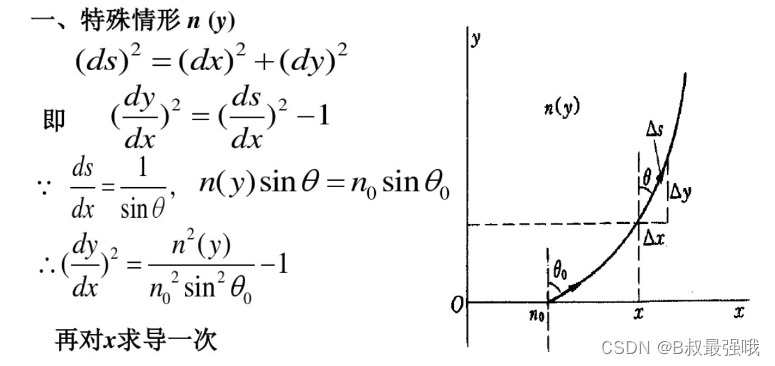
例：求聚光纤维中光线径迹

某种程度上可推得 光的波动性。可根据该情况小角近似推出聚光光纤的角度，祥见参考 视频。

---

参考内容

http://www.icourses.cn/sCourse/course_3571.html
https://wenku.baidu.com/view/280ca23943323968001c9207.html?fr=aladdin664466&ind=1&aigcsid=39662&qtype=0&lcid=1&queryKey=%E7%8E%B0%E4%BB%A3%E5%85%89%E5%AD%A6%E5%9F%BA%E7%A1%80&wkts=1708349418827&bdQuery=%E7%8E%B0%E4%BB%A3%E5%85%89%E5%AD%A6%E5%9F%BA%E7%A1%80