OpenGL 入门（五）— Transform（坐标变换）

前言

笛卡儿坐标系 (Cartesian Coordinate System)

二维笛卡儿坐标系

• 一个特殊的位置，即原点，它是整个坐标系的中心；
• 两条过原点的互相垂直的矢量，即x轴和y轴 。这些坐标轴也被称为是该坐标系的基矢量；
  

三维笛卡儿坐标系

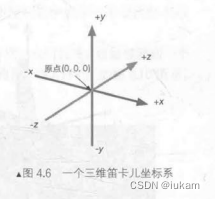
在三维笛卡儿坐标系中，我们需要定义 3个坐标轴和 1个原点。

这3个坐标轴也被称为是该坐标系的基矢量 (basis vector)。通常悄况下，这3个坐标轴之间是互相垂直的，且长度为 1，这样的基矢量被称为标准正交基 (orthonormal basis), 但这并不是
必须的。
例如，在一些坐标系中坐标轴之间互相垂直但长度不为1，这样的基矢量被称为正交基(orthogonal basis) 。

左手坐标系和右手坐标系

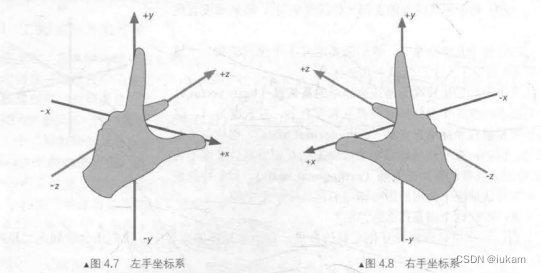
在DirectX中使用左手坐标系，在OpenGL中使用的是右手坐标系。

向量

向量最基本的定义就是一个方向。或者更正式的说，向量有一个方向(Direction)和大小(Magnitude，也叫做强度或长度)。

当用在公式中时它们通常是这样的：
$$\vec{v}=\left(\begin{array}{c}x\\ y\\ z\end{array}\right)$$

强烈推荐B站视频：线性代数的本质 - 01 - 向量究竟是什么？

向量与标量运算

标量(Scalar)只是一个数字（或者说是仅有一个分量的向量）。当把一个向量加/减/乘/除一个标量，我们可以简单的把向量的每个分量分别进行该运算。对于加法来说会像这样:
$$\left(\begin{array}{c}x\\ y\\ z\end{array}\right)+i=\left(\begin{array}{c}x+i\\ y+i\\ z+i\end{array}\right)$$
其中的+可以是+，-，·或÷，其中·是乘号。注意－和÷运算时不能颠倒（标量-/÷向量），因为颠倒的运算是没有定义的。

向量取反

对一个向量取反(Negate)会将其方向逆转。我们在一个向量的每个分量前加负号就可以实现取反了（或者说用-1数乘该向量）：
$$-\vec{v}=-\left(\begin{array}{c}{v}_x\\ v_y\\ v_z\end{array}\right)=\left(\begin{array}{c}-v_x\\ -v_y\\ -v_z\end{array}\right)$$

向量加减

向量的加法可以被定义为是分量的(Component-wise)相加，即将一个向量中的每一个分量加上另一个向量的对应分量：
$$\vec{v}=\left(\begin{array}{c}x\\ y\\ z\end{array}\right),\vec{k}=\left(\begin{array}{c}a\\ b\\ c\end{array}\right)\to \vec{v}+\vec{k}=\left(\begin{array}{c}x+a\\ y+b\\ z+c\end{array}\right)$$

示例图：

向量的减法等于加上第二个向量的相反向量：
$$\vec{v}=\left(\begin{array}{c}x\\ y\\ z\end{array}\right),\vec{k}=\left(\begin{array}{c}a\\ b\\ c\end{array}\right)\to \vec{v}+(-\vec{k})=\left(\begin{array}{c}x+(-a)\\ y+(-b)\\ z+(-c)\end{array}\right)$$
示例图：

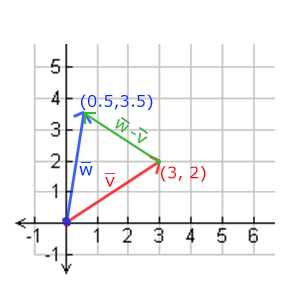
长度

使用勾股定理(Pythagoras Theorem)来获取向量的长度(Length)/大小(Magnitude)。
公式如下：
$$||\vec{v}||=\sqrt{x{}^2+y{}^2}$$
$||\vec{v}||$表示向量$\vec{v}$的长度，我们也可以加上$z^2$把这个公式拓展到三维空间。

有一个特殊类型的向量叫做单位向量(Unit Vector)。单位向量有一个特别的性质——它的长度是1。可以用任意向量的每个分量除以向量的长度得到它的单位向量$\hat{n}$：

$$\hat{n}=\frac{\vec{v}}{||\vec{v}||}$$

向量相乘

强烈推荐B站视频：线性代数的本质 - 07 - 点积与对偶性

点乘(Dot Product)

两个向量的点乘等于它们的数乘结果乘以两个向量之间夹角的余弦值。
公式：
$$\vec{v}\cdot \vec{k}=||\vec{v}||\cdot ||\vec{k}||\cdot \cos \theta$$
通过上面点乘定义式可推出，计算两个非单位向量的夹角：
$$\cos \theta =\frac{\vec{v}\cdot \vec{k}}{||\vec{v}||\cdot ||\vec{k}||}$$

点积只定义了两个向量的夹角，使用点乘可以很容易测试两个向量是否正交(Orthogonal)或平行（正交意味着两个向量互为直角）。

叉乘(Cross Product)

叉乘只在3D空间中有定义，它需要两个不平行向量作为输入，生成一个正交于两个输入向量的第三个向量。

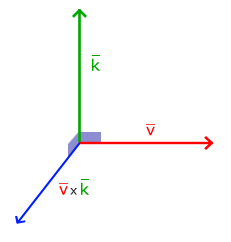
公式：
$$\left(\begin{array}{c}{A}_x\\ A_y\\ A_z\end{array}\right)\times \left(\begin{array}{c}{B}_x\\ B_y\\ B_z\end{array}\right)=\left(\begin{array}{c}{A}_y\cdot B_z-A_z\cdot B_y\\ A_z\cdot B_x-A_x\cdot B_z\\ A_x\cdot B_y-A_y\cdot B_x\end{array}\right)$$

矩阵

简单来说矩阵就是一个矩形的数字、符号或表达式数组。矩阵中每一项叫做矩阵的元素(Element)。下面是一个3×3矩阵的例子：
$$\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right]$$

矩阵的加减

矩阵与标量之间的加减定义如下：
$$\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]+i=\left[\begin{array}{cc}{a}_{11}+i& a_{12}+i\\ a_{21}+i& a_{22}+i\end{array}\right]$$

标量值要加到矩阵的每一个元素上。矩阵与标量的减法也相似：

$$\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]-i=\left[\begin{array}{cc}{a}_{11}-i& a_{12}-i\\ a_{21}-i& a_{22}-i\end{array}\right]$$

注意，数学上是没有矩阵与标量相加减的运算的，但是很多线性代数的库都对它有支持（比如说我们用的GLM）。

加法和减法只对同维度的矩阵才是有意义的。

矩阵与矩阵之间的加法：
$$\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]+\left[\begin{array}{cc}{b}_{11}& b_{12}\\ b_{21}& b_{22}\end{array}\right]=\left[\begin{array}{cc}{a}_{11}+b_{11}& a_{12}+b_{12}\\ a_{21}+b_{21}& a_{22}+b_{22}\end{array}\right]$$
矩阵与矩阵之间的减法：
$$\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]-\left[\begin{array}{cc}{b}_{11}& b_{12}\\ b_{21}& b_{22}\end{array}\right]=\left[\begin{array}{cc}{a}_{11}-b_{11}& a_{12}-b_{12}\\ a_{21}-b_{21}& a_{22}-b_{22}\end{array}\right]$$

矩阵的数乘

矩阵与标量之间的乘法也是矩阵的每一个元素分别乘以该标量。
下面的例子展示了乘法的过程：
$$\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]\cdot i=\left[\begin{array}{cc}{a}_{11}\cdot i& a_{12}\cdot i\\ a_{21}\cdot i& a_{22}\cdot i\end{array}\right]$$

简单来说，标量就是用它的值缩放(Scale)矩阵的所有元素.

矩阵相乘

矩阵相乘的限制：

• 只有当左侧矩阵的列数与右侧矩阵的行数相等，两个矩阵才能相乘。
• 矩阵相乘不遵守交换律(Commutative)，也就是说A⋅B≠B⋅A。

矩阵与矩阵之间相乘：
$$\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]\cdot \left[\begin{array}{cc}{b}_{11}& b_{12}\\ b_{21}& b_{22}\end{array}\right]=\left[\begin{array}{cc}{a}_{11}\cdot b_{11}+a_{12}\cdot b_{21}& a_{11}\cdot b_{12}+a_{12}\cdot b_{22}\\ a_{12}\cdot b_{11}+a_{22}\cdot b_{21}& a_{12}\cdot b_{12}+a_{22}\cdot b_{22}\end{array}\right]$$

看完上面，肯定有点慌。如果矩阵的维度是(n, m)，n等于左侧矩阵的行数，m等于右侧矩阵的列数。在用手动计算是非常头疼的事，可以看到，矩阵相乘非常繁琐而容易出错（这也是我们通常让计算机做这件事的原因）。

这里推荐两个视频可供参考：

线性代数的本质 - 03 - 矩阵与线性变换

线性代数的本质 - 04 - 矩阵乘法与线性变换复合

矩阵与向量相乘

单位矩阵

最简单的变换矩阵就是单位矩阵(Identity Matrix)。单位矩阵是一个除了对角线以外都是0的N×N矩阵。在下式中可以看到，这种变换矩阵使一个向量完全不变：
$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\cdot \left(\begin{array}{c}x\\ y\\ z\\ w\end{array}\right)=\left[\begin{array}{c}x\\ y\\ z\\ w\end{array}\right]$$
向量看起来完全没变。从乘法法则来看就很容易理解来：第一个结果元素是矩阵的第一行的每个元素乘以向量的每个对应元素。

缩放

对一个向量进行缩放(Scaling)就是对向量的长度进行缩放，而保持它的方向不变。
如果我们把缩放变量表示为$(S_1,S_2,S_3)$，我们可以为任意向量$(x,y,z)$，定义一个缩放矩阵：
$$\left[\begin{array}{cccc}{S}_1& 0& 0& 0\\ 0& S_2& 0& 0\\ 0& 0& S_3& 0\\ 0& 0& 0& 1\end{array}\right]\cdot \left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left[\begin{array}{c}{S}_1\cdot x\\ S_2\cdot y\\ S_3\cdot z\\ 1\end{array}\right]$$

注意，第四个缩放向量仍然是1，因为在3D空间中缩放w分量是无意义的。

位移

位移(Translation)是在原始向量的基础上加上另一个向量从而获得一个在不同位置的新向量的过程，从而在位移向量基础上移动了原始向量。

和缩放矩阵一样，在4×4矩阵上有几个特别的位置用来执行特定的操作，对于位移来说它们是第四列最上面的3个值。如果我们把位移向量表示为$(T_x,T_y,T_z)$，我们就能把位移矩阵定义为：

$$\left[\begin{array}{cccc}1& 0& 0& T_x\\ 0& 1& 0& T_y\\ 0& 0& 1& T_z\\ 0& 0& 0& 1\end{array}\right]\cdot \left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left[\begin{array}{c}x+T_x\\ y+T_y\\ z+T_z\\ 1\end{array}\right]$$

旋转

旋转(Rotation)稍复杂些，如果你想知道旋转矩阵是如何构造出来的，荐去看可汗学院线性代数的视频。

2D或3D空间中的旋转用角(Angle)来表示。角可以是角度制或弧度制的，周角是360角度或2 PI弧度。

大多数旋转函数需要用弧度制的角，但幸运的是角度制的角也可以很容易地转化为弧度制的：
弧度转角度：角度 = 弧度 * (180.0f / PI)
角度转弧度：弧度 = 角度 * (PI / 180.0f)
PI约等于3.14159265359。

在3D空间中旋转需要定义一个角和一个旋转轴(Rotation Axis)。物体会沿着给定的旋转轴旋转特定角度。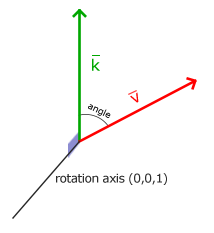
旋转矩阵在3D空间中每个单位轴都有不同定义，旋转角度用θ
表示：
沿x轴旋转：
$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos\theta & -sin\theta & 0\\ 0& sin\theta & cos\theta & 0\\ 0& 0& 0& 1\end{array}\right]\cdot \left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left[\begin{array}{c}x\\ cos\theta \cdot y-sin\theta \cdot z\\ sin\theta \cdot y+cos\theta \cdot z\\ 1\end{array}\right]$$

沿y轴旋转：
$$\left[\begin{array}{cccc}cos\theta & 0& sin\theta & 0\\ 0& 1& 0& 0\\ -sin\theta & 0& cos\theta & 0\\ 0& 0& 0& 1\end{array}\right]\cdot \left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left[\begin{array}{c}cos\theta \cdot x+sin\theta \cdot z\\ y\\ -sin\theta \cdot x+cos\theta \cdot z\\ 1\end{array}\right]$$

沿z轴旋转：
$$\left[\begin{array}{cccc}cos\theta & -sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\cdot \left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left[\begin{array}{c}cos\theta \cdot x-sin\theta \cdot y\\ sin\theta \cdot x+cos\theta \cdot y\\ z\\ 1\end{array}\right]$$

利用旋转矩阵我们可以把任意位置向量沿一个单位旋转轴进行旋转。也可以将多个矩阵复合，比如先沿着x轴旋转再沿着y轴旋转。但是这会很快导致一个问题——万向节死锁（Gimbal Lock，可以看看这个视频（优酷）来了解）。

一个（超级麻烦的）矩阵是存在的，见下面这个公式，其中(Rx,Ry,Rz)
代表任意旋转轴：

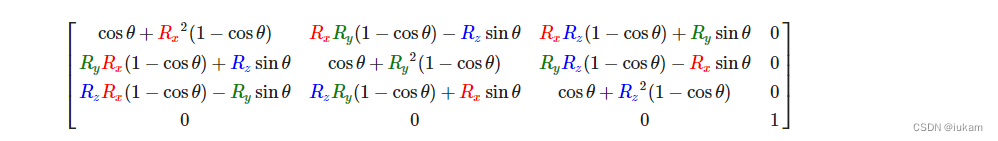
GLM函数库

GLM是OpenGL Mathematics的缩写，它是一个只有头文件的库，也就是说我们只需包含对应的头文件就行了，不用链接和编译。GLM可以在它们的网站上下载。把头文件的根目录复制到你的includes文件夹，然后你就可以使用这个库了。

使用GLM函数库

#include <iostream>

//引入头文件
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>

int main()
{
    // 把一个向量(1, 0, 0)位移(1, 1, 0)个单位
    glm::vec4 initVec(1.0f, 0.0f, 0.0f, 1.0f);
    glm::mat4 transMove = glm::mat4(1.0f);
    transMove = glm::translate(transMove, glm::vec3(1.0f, 1.0f, 0.0f));
    initVec = transMove * initVec;
    std::cout << " x: " << initVec.x << " y: " << initVec.y << " z: " << initVec.z << std::endl;

    return 0;
}

输出结果：

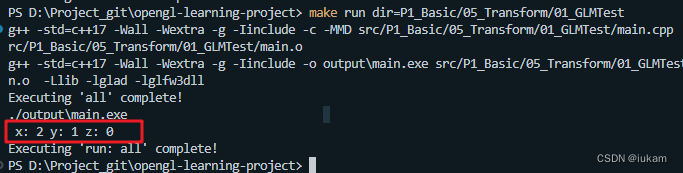
一个展示Demo：

完整源码

文件路径：

顶点着色器：

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;

out vec2 TexCoord;

uniform mat4 transform;

void main()
{
	gl_Position = transform * vec4(aPos, 1.0);
	TexCoord = vec2(aTexCoord.x, aTexCoord.y);
}

片元着色器：

#version 330 core
out vec4 FragColor;

in vec2 TexCoord;

// texture samplers
uniform sampler2D texture1;
uniform sampler2D texture2;

void main()
{
    //在两个纹理之间进行线性插值(80% container, 20% awesomeface)
    FragColor=mix(texture(texture1,TexCoord),texture(texture2,TexCoord),.2);
}

主程序：

#include <glad/glad.h>
#include <GLFW/glfw3.h>

#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>

#define STB_IMAGE_IMPLEMENTATION
#include <stb_image.h>

#include <shader_s.h>

void InitGLFW();
bool CreateWindow();
bool InitGLAD();
// 窗口大小改变时调用
void framebuffer_size_callback(GLFWwindow *window, int width, int height);
void processInput(GLFWwindow *window);

// settings 窗口宽高
const unsigned int SCR_WIDTH = 800;
const unsigned int SCR_HEIGHT = 600;

GLFWwindow *window;

int main()
{
    InitGLFW(); // 初始化GLFW

    bool isCreated = CreateWindow(); // 创建一个窗口对象
    if (!isCreated)
        return -1;
    bool isGLAD = InitGLAD(); // 初始化GLAD，传入加载系统相关opengl函数指针的函数
    if (!isGLAD)
        return -1;

    // 构建和编译着色程序
    Shader ourShader("shader/P1_Basic/05_Transform/transform.vs", "shader/P1_Basic/05_Transform/transform.fs");

    // 设置顶点数据(和缓冲区)并配置顶点属性
    // 1.顶点输入
    float vertices[] = {
        // positions          // texture coords
        0.5f, 0.5f, 0.0f, 1.0f, 1.0f,   // top right
        0.5f, -0.5f, 0.0f, 1.0f, 0.0f,  // bottom right
        -0.5f, -0.5f, 0.0f, 0.0f, 0.0f, // bottom left
        -0.5f, 0.5f, 0.0f, 0.0f, 1.0f   // top left
    };
    unsigned int indices[] = {
        0, 1, 3, // first triangle
        1, 2, 3  // second triangle
    };
    unsigned int VBO, VAO, EBO;
    glGenVertexArrays(1, &VAO); // 生成一个VAO对象
    glGenBuffers(1, &VBO);      // 生成一个VBO对象
    glGenBuffers(1, &EBO);      // 生成一个EBO对象

    glBindVertexArray(VAO);
    // 绑定VAO
    glBindBuffer(GL_ARRAY_BUFFER, VBO);                                        // 绑定VBO
    glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW); // 将顶点数据复制到缓冲区中

    glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, EBO); // 绑定EBO
    glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(indices), indices, GL_STATIC_DRAW);

    // 4.配置位置属性
    glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 5 * sizeof(float), (void *)0);
    glEnableVertexAttribArray(0);
    // 5.   纹理属性
    glVertexAttribPointer(1, 2, GL_FLOAT, GL_FALSE, 5 * sizeof(float), (void *)(3 * sizeof(float)));
    glEnableVertexAttribArray(1);

    // 加载和创建纹理
    unsigned int texture1, texture2;
    // 加载第一张纹理图片
    glGenTextures(1, &texture1);            // 生成纹理
    glBindTexture(GL_TEXTURE_2D, texture1); // 绑定纹理
    // 设置纹理环绕方式
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT); // x轴
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT); // y轴
    // 设置纹理过滤方式
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR); // 缩小
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR); // 放大
    // 加载纹理图片,创建纹理和生成多级渐远纹理
    int width, height, nrChannels;
    stbi_set_flip_vertically_on_load(true); // stb_image.h能够在图像加载时帮助我们翻转y轴
    unsigned char *data = stbi_load("image/04_Textures/container.jpg", &width, &height, &nrChannels, 0);
    if (data)
    {
        // 生成纹理
        glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data);
        // 生成多级渐远纹理
        glGenerateMipmap(GL_TEXTURE_2D);
    }
    else
    {
        std::cout << "Failed to load texture" << std::endl;
    }
    // 释放图像内存
    stbi_image_free(data);

    // 加载第二张纹理图片
    glGenTextures(1, &texture2);            // 生成纹理
    glBindTexture(GL_TEXTURE_2D, texture2); // 绑定纹理
    // 设置纹理环绕方式
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT); // x轴
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT); // y轴
    // 设置纹理过滤方式
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR); // 缩小
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR); // 放大
    // 加载纹理图片,创建纹理和生成多级渐远纹理
    data = stbi_load("image/04_Textures/awesomeface.png", &width, &height, &nrChannels, 0);
    if (data)
    {
        // 注意，awesomeface.png具有透明度，因此有一个alpha通道，所以一定要告诉OpenGL数据类型是GL_RGBA
        glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGBA, GL_UNSIGNED_BYTE, data);
        // 生成多级渐远纹理
        glGenerateMipmap(GL_TEXTURE_2D);
    }
    else
    {
        std::cout << "Failed to load texture" << std::endl;
    }
    // 释放图像内存
    stbi_image_free(data);

    // 告诉opengl每个采样器属于哪个纹理单元(只需要做一次)
    ourShader.use();
    ourShader.setInt("texture1", 0);
    ourShader.setInt("texture2", 1);

    // 循环渲染
    while (!glfwWindowShouldClose(window))
    {
        // 输入
        processInput(window);

        // 渲染
        // 清除颜色缓冲
        glClearColor(0.2f, 0.3f, 0.3f, 1.0f);
        glClear(GL_COLOR_BUFFER_BIT);

        // 在相应的纹理单元上绑定纹理
        glActiveTexture(GL_TEXTURE0);
        glBindTexture(GL_TEXTURE_2D, texture1);
        glActiveTexture(GL_TEXTURE1);
        glBindTexture(GL_TEXTURE_2D, texture2);

        // 创建 坐标变换
        glm::mat4 transform = glm::mat4(1.0f); // 确保首先将矩阵初始化为单位矩阵
        transform = glm::translate(transform, glm::vec3(0.5f, -0.5f, 0.0f));
        transform = glm::rotate(transform, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));

        ourShader.use();

        unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform");
        glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(transform));

        // 绘制三角形
        glBindVertexArray(VAO);                              // 绑定VAO
        glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_INT, 0); // 绘制三角形

        // 检查并调用事件，交换缓冲
        glfwSwapBuffers(window);
        glfwPollEvents();
    }

    // 可选:一旦资源超出其用途，就取消分配所有资源:
    glDeleteVertexArrays(1, &VAO);
    glDeleteBuffers(1, &VBO);

    // 释放/删除之前的分配的所有资源
    glfwTerminate();
    std::cout << "Hello, World!" << std::endl;
    return 0;
}

void InitGLFW()
{
    // 初始化GLFW
    glfwInit();
    // 配置GLFW  第一个参数代表选项的名称，我们可以从很多以GLFW_开头的枚举值中选择；
    // 第二个参数接受一个整型，用来设置这个选项的值。
    glfwWindowHint(GLFW_CONTEXT_VERSION_MAJOR, 3);
    glfwWindowHint(GLFW_CONTEXT_VERSION_MINOR, 3);
    glfwWindowHint(GLFW_OPENGL_PROFILE, GLFW_OPENGL_CORE_PROFILE);
    // glfwWindowHint(GLFW_OPENGL_FORWARD_COMPAT, GL_TRUE);
}
bool CreateWindow()
{
    // 创建一个窗口对象
    window = glfwCreateWindow(800, 600, "LearnOpenGL", NULL, NULL);
    if (window == NULL)
    {
        std::cout << "Failed to create GLFW window" << std::endl;
        // 创建失败，终止程序
        glfwTerminate();
        return false;
    }
    // 将我们窗口的上下文设置为当前线程的主上下文
    glfwMakeContextCurrent(window);
    // 设置窗口大小改变时的回调函数
    glfwSetFramebufferSizeCallback(window, framebuffer_size_callback);
    return true;
}
bool InitGLAD()
{
    // 初始化GLAD，传入加载系统相关opengl函数指针的函数
    if (!gladLoadGLLoader((GLADloadproc)glfwGetProcAddress))
    {
        std::cout << "Failed to initialize GLAD" << std::endl;
        // 初始化失败，终止程序
        return false;
    }
    return true;
}

// 窗口大小改变时调用
void framebuffer_size_callback(GLFWwindow *window, int width, int height)
{
    // 设置窗口的维度
    glViewport(0, 0, width, height);
}

// 输入
void processInput(GLFWwindow *window)
{
    // 当用户按下esc键，我们设置window窗口的windowShouldClose属性为true
    // 关闭应用程序
    if (glfwGetKey(window, GLFW_KEY_ESCAPE) == GLFW_PRESS)
        glfwSetWindowShouldClose(window, true);
}