基于System Verilog的8点FFT实现

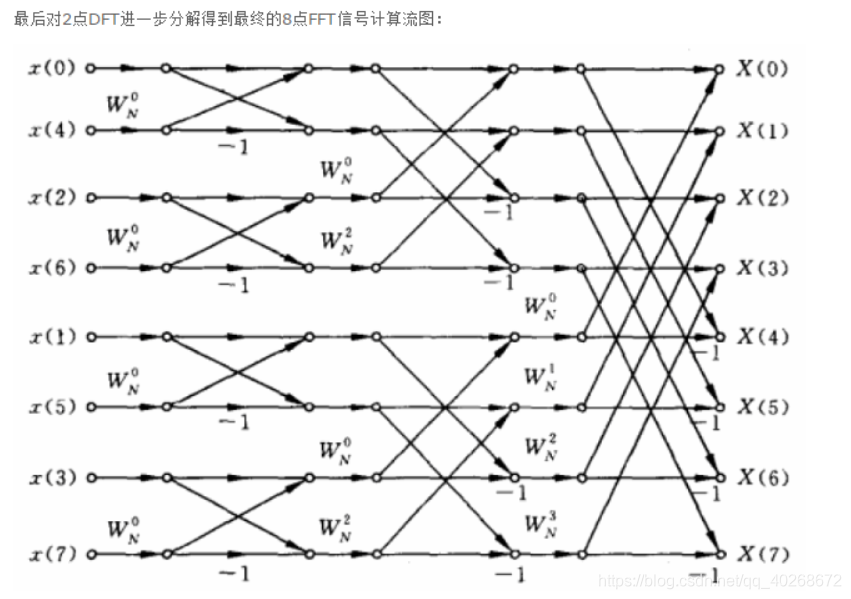
我们采用system verilog实现一个8点的基于蝶形运算单元的FFT变换，如下图，是蝶形运算单元的示意图。

然后，由于FFT涉及复数运算，因此，我们编写如下复数类型以及运算符的一个包:

`timescale 1ns / 1ps
//
// Company: 
// Engineer: 
// 
// Create Date: 2021/07/22 11:57:16
// Design Name: 
// Module Name: complex_type
// Project Name: 
// Target Devices: 
// Tool Versions: 
// Description: 
// 
// Dependencies: 
// 
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
// 
//
package complex_type;    
    parameter DATA_WIDTH = 32;
    //复数结构体类型
    typedef struct {
    logic signed [DATA_WIDTH-1:0]  r;
    logic signed [DATA_WIDTH-1:0]  i;
    } Complex;
    //复数运算函数
    //定义复数乘法
    function Complex complex_mul(Complex a,Complex b);             //(a.r+i*a.i)x(b.r+i*b.i)
        Complex res;
        //为防止溢出，扩展到64位再进行乘法
        logic [2*DATA_WIDTH-1:0] expand_a_r;
        logic [2*DATA_WIDTH-1:0] expand_a_i;
        logic [2*DATA_WIDTH-1:0] expand_b_r;
        logic [2*DATA_WIDTH-1:0] expand_b_i;
        // $display("a=(%d,%d),b=(%d,%d)",a.r,a.i,b.r,b.i);
        expand_a_r={{32{a.r[31]}},a.r};
        expand_a_i={{32{a.i[31]}},a.i};
        expand_b_r={{32{b.r[31]}},b.r};
        expand_b_i={{32{b.i[31]}},b.i};
        res.r=(expand_a_r*expand_b_r-expand_a_i*expand_b_i)>>>16;
        res.i=(expand_a_r*expand_b_i+expand_a_i*expand_b_r)>>>16;
        // $display("res=(%d,%d)",res.r,res.i);
        return res;
    endfunction
    //定义复数加法
    function Complex complex_add(Complex a,Complex b);
        Complex res;
        res.r=a.r+b.r;
        res.i=a.i+b.i;
        return res;
    endfunction
    //定义复数减法
    function Complex complex_sub(Complex a,Complex b);
        Complex res;
        res.r=a.r-b.r;
        res.i=a.i-b.i;
        return res;
    endfunction
endpackage

 然后是我们的FFT模块:

`timescale 1ns / 1ps
//
// Company: 
// Engineer: 
// 
// Create Date: 2021/07/22 09:50:53
// Design Name: 
// Module Name: FFT
// Project Name: 
// Target Devices: 
// Tool Versions: 
// Description: 
// 
// Dependencies: 
// 
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
// 
//

import complex_type::* ;

module FFT
#(parameter DATA_WIDTH = 32,
  parameter N = 8,
  parameter STAGE = 3)
(
input logic clk,
input logic rst,
input logic valid,
input Complex data_in [0:N-1],
output Complex data_out [0:N-1],
output logic ready
    );
logic valid_ff1;
logic valid_ff2;
logic valid_ff3;
//定义旋转因子常量
Complex WN0 = '{65536,0};           
Complex WN1 = '{46340,-46340};
Complex WN2 = '{0,-65535};
Complex WN3 = '{-46340,-46341};
//中间结果
Complex tmp [0:STAGE][0:N-1];                                          //STAGE=log2(N),为蝶形运算单元的级数
//蝶形运算
//第1级 tmp[0]-->tmp[1]
always_ff@(posedge clk)                 //第一级,蝶形单元跨度为1=2^0
for(int i=0;i<N;i+=2)
begin
    tmp[1][i]<=complex_add(tmp[0][i],complex_mul(tmp[0][i+1],WN0));
    tmp[1][i+1]<=complex_sub(tmp[0][i],complex_mul(tmp[0][i+1],WN0));
    // $write("mult=%d,%d\n",complex_mul(tmp[0][1],WN0).r,complex_mul(tmp[0][1],WN0).i);
    // for(int j=0;j<2;j++)
    //     $write("i=%d,%d,%d\n",i+j,tmp[1][i+j].r>>>16,tmp[1][i+j].i>>>16);
end
//第2级 tmp[1]-->tmp[2]                 
always_ff@(posedge clk)
for(int i=0;i<N;i+=4)                   //第二级，蝶形单元跨度为2=2^1
begin
    tmp[2][i]<=complex_add(tmp[1][i],complex_mul(tmp[1][i+2],WN0));
    tmp[2][i+1]<=complex_add(tmp[1][i+1],complex_mul(tmp[1][i+3],WN2));
    tmp[2][i+2]<=complex_sub(tmp[1][i],complex_mul(tmp[1][i+2],WN0));
    tmp[2][i+3]<=complex_sub(tmp[1][i+1],complex_mul(tmp[1][i+3],WN2));
end
//第3级 tmp[2]-->tmp[3]
always_ff@(posedge clk)
for(int i=0;i<N;i+=8)                  //第三级，蝶形单元跨度为4=2^2                                            第i级span=2^(i-1)
begin
    tmp[3][i]<=complex_add(tmp[2][i],complex_mul(tmp[2][i+4],WN0));
    tmp[3][i+1]<=complex_add(tmp[2][i+1],complex_mul(tmp[2][i+5],WN1));
    tmp[3][i+2]<=complex_add(tmp[2][i+2],complex_mul(tmp[2][i+6],WN2));
    tmp[3][i+3]<=complex_add(tmp[2][i+3],complex_mul(tmp[2][i+7],WN3));
    tmp[3][i+4]<=complex_sub(tmp[2][i],complex_mul(tmp[2][i+4],WN0));
    tmp[3][i+5]<=complex_sub(tmp[2][i+1],complex_mul(tmp[2][i+5],WN1));
    tmp[3][i+6]<=complex_sub(tmp[2][i+2],complex_mul(tmp[2][i+6],WN2));
    tmp[3][i+7]<=complex_sub(tmp[2][i+3],complex_mul(tmp[2][i+7],WN3));
end
//data_out
always_comb 
begin
    for(int i=0;i<N;i++)
        data_out[i]=tmp[3][i];    
end
//data_in,bit reverse
always_ff@(posedge clk)
begin
    tmp[0][0]<=data_in[0];
    tmp[0][1]<=data_in[4];
    tmp[0][2]<=data_in[2];
    tmp[0][3]<=data_in[6];
    tmp[0][4]<=data_in[1];
    tmp[0][5]<=data_in[5];
    tmp[0][6]<=data_in[3];
    tmp[0][7]<=data_in[7];
end
//ready,延迟为4个周期，一个周期bit reverse,3个周期计算
always_ff@(posedge clk)
    {ready,valid_ff3,valid_ff2,valid_ff1}<={valid_ff3,valid_ff2,valid_ff1,valid};
endmodule

这是一个全流水的FFT计算模块，II=1个时钟周期，ready信号为高时表示结果有效。延迟为4个周期，第一个周期进行bit reverse操作，第2，3，4个周期，则是FFT蝶形运算的3个stage。

最后，是testbench:(本FFT模块采用32位有符号定点数实现，小数部分占16位）

`timescale 1ns / 1ps
//
// Company: 
// Engineer: 
// 
// Create Date: 2021/07/22 12:31:14
// Design Name: 
// Module Name: test
// Project Name: 
// Target Devices: 
// Tool Versions: 
// Description: 
// 
// Dependencies: 
// 
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
// 
//

import complex_type::*;

module test;
parameter N = 8;
Complex IN [0:N-1];
Complex OUT [0:N-1];
logic clk;
logic rst;
logic valid;
logic ready;

initial begin
    clk=0;
    forever begin
        #5 clk=~clk;
    end
end

initial begin
    rst=1;
    #20
    rst=0;
end

initial begin
    for(int i=0;i<N;i++)
    begin
        IN[i].r=(i<<12);
        IN[i].i=0;
    end
end

initial begin
    valid=1;
    #10
    valid=0;
end

always_ff@(posedge clk)
if(ready)
begin
    for(int i=0;i<N;i++)
        $display("data_out[%d]=%f+%f*i",i,integer'(OUT[i].r)/65536.0,integer'(OUT[i].i)/65536.0);
end
FFT U(
.clk(clk),
.rst(rst),
.data_in(IN),
.data_out(OUT),
.valid(valid),
.ready(ready)
);

endmodule

仿真结果如下:

 

其中，观察定点数的值可以通过如下方式实现:右键波形--->Radix---->RealSettings,然后选择定点数以及小数位数。

最后是C++的运行结果，可以看到，和仿真结果是一致的。