图论——极图和托兰定理

一、$l$部图的概念与特征

$l$部图定义：

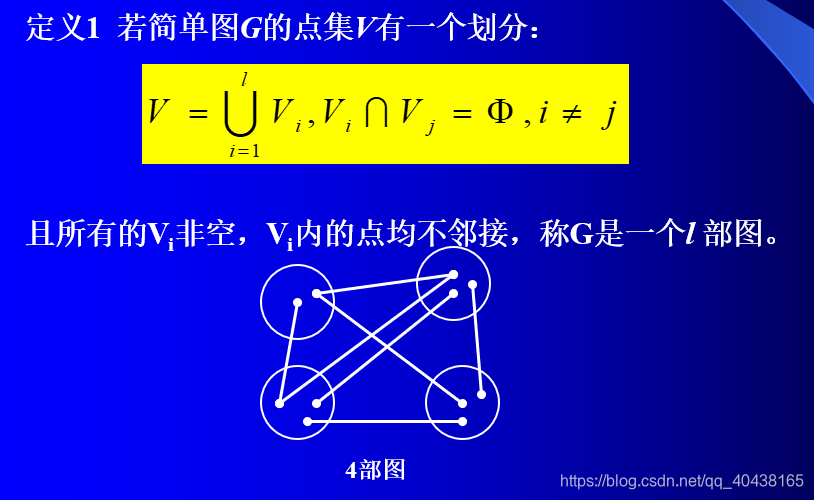
完全$l$部图定义：
如果在一个$l$部图G中，任意部$V_i$中的每个顶点同G中其它各部中的每个顶点均邻接，称G为完全$l$部图。记作： $G=K_{n_1,n_2,\cdots ,n_l}(n_i=|V_i|,1\le i\le l)$
完全$l$等部图：
各部顶点数相同的完全$l$部图
n阶完全$l$几乎等部图：
各部顶点数差值不超过1，记为$T_{l,n}$

定理1：连通偶图的2部划分是唯一的。
定理2：n阶完全偶图 $K_{n_1,n_2}$的边数$m=n_1{n}_2$,且有：$m\le [\frac{n^2}{4}]$
定理3：n阶l部图G有最多边数的充要条件是$G≌T_{l,n}$。

二、托兰定理及其应用

定义：设G和H是两个n阶图，称G度弱于H，如果存在双射μ：V(G)→V(H),使得：$$\forall v\in V(G),有d_G(v)\le d_H(\mu (v))$$则称G度弱于H，一定有$m(G)\le m(H)$。
定理4：若n阶简单图G不包含$K_{l+1}$，则G度弱于某个完全 l 部图 H，且若G具有与 H 相同的度序列，则:$G≌H$。

托兰定理：若G是简单图，并且不包含$K_{l+1}$,则：$m(G)\le m(T_{l,n})$，仅当$G≌T_{l,n}$时有$m(G)=m(T_{l,n})$。