随着联结主义学派的兴起,概率统计已经取代了数理逻辑,成为了人工智能研究的主流工具
数理统计的关注点是 无处不在的可能性
- 对随机事件发生的可能性进行规范的数学描述是概率论的公理化过程
频率学派认为先验分布式固定的,模型参数靠最大似然估计计算
贝叶斯学派认为先验分布是随机的,模型参数靠后验概率最大化计算
3.1 概念
3.1.1 随机事件e
-
在相同条件下可重复执行
相同条件下,事件发生的可能性不变
-
事先知道所有实验结果
-
实验开始前,不知道本次实验结果
3.1.2 样本空间
随机实验E的所有结果构成的集合 S = { e } S=\{e\} S={e}
3.1.3 事件的表示——Venn图
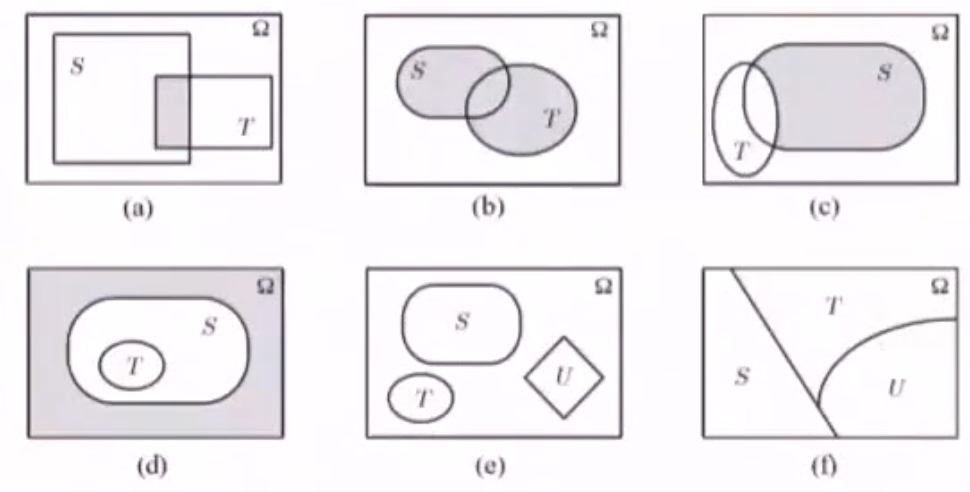
- S ⋂ T S\bigcap T S⋂T
- S ⋃ T S\bigcup T S⋃T
- S − T = S ⋂ T ‾ S-T=S\bigcap \overline{T} S−T=S⋂T
- S ‾ ⋂ T ‾ \overline{S}\bigcap \overline{T} S⋂T
- S,T,U相互独立
- S,T,U是 Ω \Omega Ω 的一个划分
3.1.4 事件与概率

将事件映射到实数域
3.1.5 概率与频率
A A A 在 N N N 次实验中发生频率 f n ( A ) = n A —— A 发生的次数 N ——总的发生次数 f_n(A)=\frac{n_A——A发生的次数}{N——总的发生次数} fn(A)=N——总的发生次数nA——A发生的次数
大数定理 : f n ( A ) f_n(A) fn(A) 的稳定值 P P P 为 A A A 发生的概率 f n ( A ) → n → ∞ p ( A ) f_n(A)\xrightarrow{n\rightarrow \infty}p(A) fn(A)n→∞p(A)
- 随着重复试验次数的增加,特定事件出现的频率值就会呈现出稳定性,逐渐趋近于某个常数
概率:一个可独立重复的随机试验中,单个结果出现频率的极限
3.1.6 古典概率
随机试验E结果只包含有限个基本事件,且每个基本事件发生的可能性相同。
p
(
A
)
=
∣
A
∣
∣
Ω
∣
{
排列:
有序地选择
n
个
A
m
n
=
m
!
(
m
−
n
)
!
组合:
无序地选择
n
个
C
m
n
=
m
!
n
!
(
m
−
n
)
!
p(A)=\frac{\vert A\vert}{\vert \Omega\vert}\quad\left\{ \begin{aligned} &排列:&有序地选择n个&\quad A_{m}^n=\frac{m!}{(m-n)!}\\ &组合:&无序地选择n个&\quad C_{m}^n=\frac{m!}{n!(m-n)!} \end{aligned} \right.
p(A)=∣Ω∣∣A∣⎩
⎨
⎧排列:组合:有序地选择n个无序地选择n个Amn=(m−n)!m!Cmn=n!(m−n)!m!
只针对单个随机事件
eg:8个球,摸到每个球概率相等,1-8号,其中1-3为红球,4-8为黄球
设事件 A A A 表示摸到红球,摸到红球的概率表示为 p ( A ) = ∣ A ∣ ∣ Ω ∣ = 3 8 p(A)=\frac{\vert A\vert}{\vert \Omega\vert}=\frac{3}{8} p(A)=∣Ω∣∣A∣=83
3.1.7 条件概率
用于刻画两个随机事件之间的关系(类比内积,通过运算将关系映射为数值),根据已有信息对样本空间进行调整后得到的新的概率分布
P ( A ∣ B ) = P ( A B ) P ( B ) , 表示事件 A 在事件 B 已经发生的条件下发生的概率 P(A\mid B)=\frac{P(AB)}{P(B)},表示事件A在事件B已经发生的条件下发生的概率 P(A∣B)=P(B)P(AB),表示事件A在事件B已经发生的条件下发生的概率
A和B两个事件共同发生的频率称为 联合概率 ,记为
P
(
A
B
)
P(AB)
P(AB)
- 如果两个事件发生互不影响相互独立,则其联合概率 P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B)
- 对于相互独立的事件,条件概率就是自身概率 P ( A ∣ B ) = P ( A ) P(A\mid B)=P(A) P(A∣B)=P(A)
二元条件概率
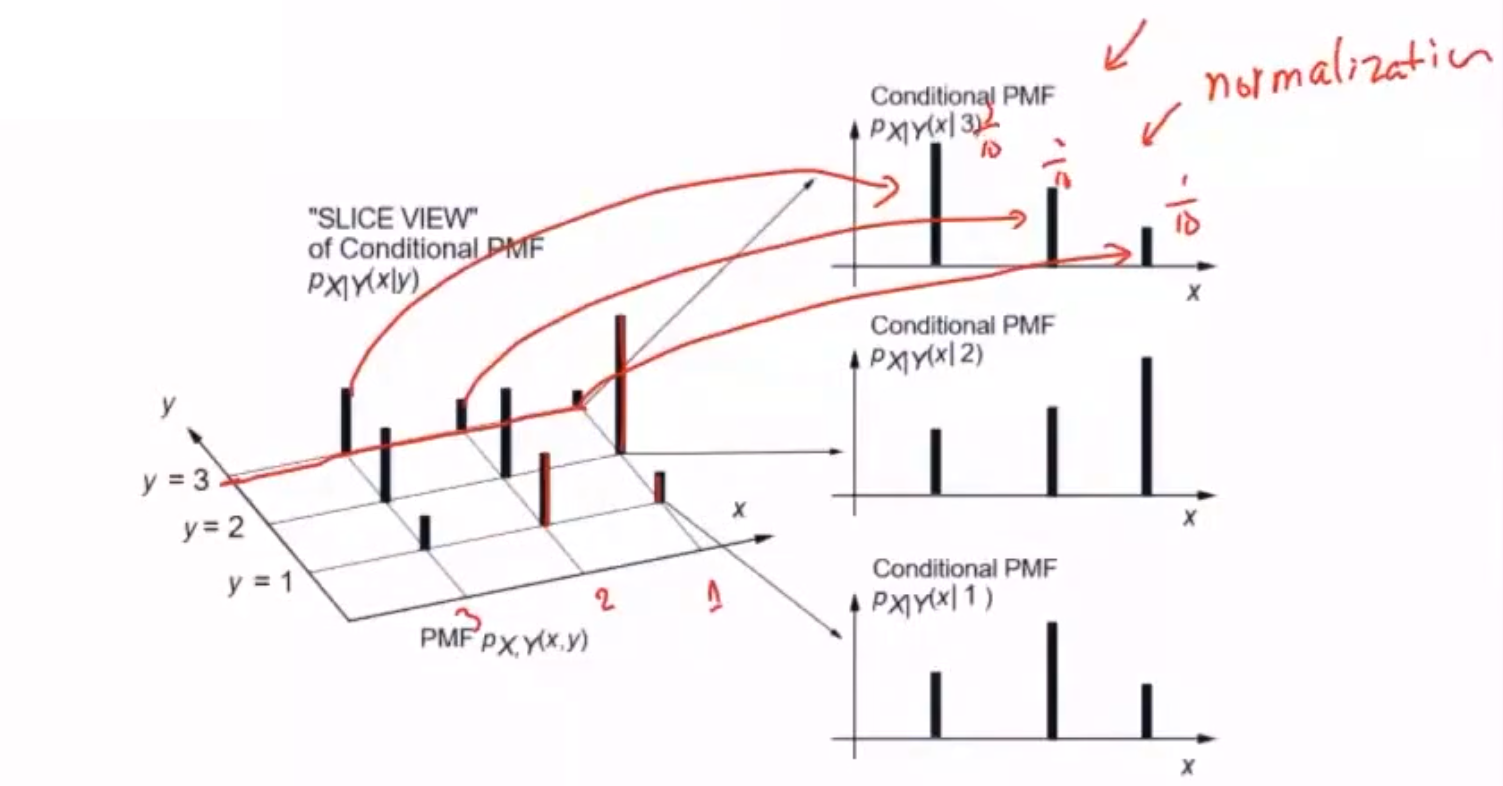
3.1.8 芝麻开门问题
5把钥匙,只有一把能打开房门,求第三次将房门打开的概率
若无放回:事件A定义为第三次打开房门,意味着前两次都没打开,该事件为B,题目所求为 P ( A B ) P(AB) P(AB) ,由条件概率 P ( A B ) = P ( A ∣ B ) P ( B ) P(AB)=P(A\vert B)P(B) P(AB)=P(A∣B)P(B) , P ( A ∣ B ) = 1 3 , P ( B ) = 4 5 × 3 4 = 3 5 P(A\vert B)=\frac{1}{3},P(B)=\frac{4}{5}\times \frac{3}{4}=\frac{3}{5} P(A∣B)=31,P(B)=54×43=53
所以 P ( A B ) = 1 5 P(AB)=\frac{1}{5} P(AB)=51
若有放回,易知每次取一把钥匙能否开门是相互独立的,即 1 5 \frac{1}{5} 51
若有放回,恰好第三次打开:恰好说明前两次没有打开, P ( A B ) = ( 4 5 × 4 5 ) × 1 5 = 16 125 P(AB)=\left(\frac{4}{5}\times \frac{4}{5}\right)\times \frac{1}{5}=\frac{16}{125} P(AB)=(54×54)×51=12516
若5把钥匙中有2把能打开,随意逐把开,且每把试过后不能重复开,那么第三次打开的概率为:第三次取得钥匙正好是2把中的一把,故 P ( A ) = C 2 1 A 4 4 A 5 5 = 2 5 P(A)=\frac{C^1_2A_4^4}{A^5_5}=\frac{2}{5} P(A)=A55C21A44=52
若第三次恰好打开:说明前两次没有打开,2把中的第1把必须是第三个位置,第2把在第4次或者第5次尝试,所以 P ( A ) = C 2 1 C 2 1 A 3 3 A 5 5 = 1 5 P(A)=\frac{C_2^1C_2^1A_3^3}{A^5_5}=\frac{1}{5} P(A)=A55C21C21A33=51
若有放回,第三次能打开的概率为:由于有放回,每次抽到正确钥匙的事件是相互独立的, P ( A ) = 2 5 P(A)=\frac{2}{5} P(A)=52
若有放回,恰好第三次打开的概率:有放回,则每次选钥匙是独立的,恰好第三次打开,说明前两次没打开, P ( A ) = 3 5 × 3 5 × 2 5 = 18 125 P(A)=\frac{3}{5}\times\frac{3}{5}\times\frac{2}{5}=\frac{18}{125} P(A)=53×53×52=12518
3.2 随机变量
3.2.1 分类
-
离散型:一个样本点代表一个事件
有限个 X = { H , T } → P ( x ) ∈ ( 0 , 1 ) X=\left\{H,T\right\}\rightarrow P(x)\in(0,1) X={H,T}→P(x)∈(0,1)
-
连续型:一个样本区间代表一个事件
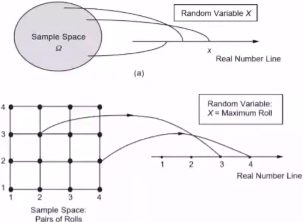
3.2.2 概率函数
P ( X ) = P r o b ( X = x ) P(X)=Prob(X=x) P(X)=Prob(X=x) 随机变量取到某一种情况的概率
离散型随机变量概率分布
-
找X的所有可能值
-
计算相应取值的概率
-
p ( x i ) ≥ 0 , i = 1 , 2 , ⋯ , n p(x_i)\ge 0,i=1,2,\cdots,n p(xi)≥0,i=1,2,⋯,n , ∑ p ( x i ) = 1 \sum p(x_i)=1 ∑p(xi)=1
x x 1 x 2 ⋯ x n p ( x i ) p ( x 1 ) p ( x 2 ) ⋯ p ( x n ) \begin{array}{c|lcr} x&x_1&x_2&\cdots&x_n\\ \hline p(x_i)&p(x_1)&p(x_2)&\cdots&p(x_n) \end{array} xp(xi)x1p(x1)x2p(x2)⋯⋯xnp(xn)
连续型随机变量
概率密度函数(PDF)
用函数形式描述事件的不确定性
由来:区间内数据的频率,将离散的数据分组,统计每一个小区间频数
→
\rightarrow
→ 频率
区间
频数
频率
a
1
f
n
(
a
1
)
p
(
a
1
)
a
2
f
n
(
a
2
)
p
(
a
2
)
⋮
⋮
⋮
a
n
f
n
(
a
n
)
p
(
a
n
)
\begin{array}{c|lcr} 区间&频数&频率\\ \hline a_1&f_n(a_1)&p(a_1)\\ a_2&f_n(a_2)&p(a_2)\\ \vdots&\vdots&\vdots\\ a_n&f_n(a_n)&p(a_n)\\ \end{array}
区间a1a2⋮an频数fn(a1)fn(a2)⋮fn(an)频率p(a1)p(a2)⋮p(an)
绘制频率直方图
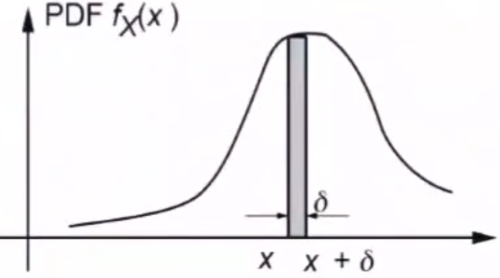
当数据足够多,区间可划分地足够小,可将频直方图近似为一条曲线,即概率密度 f X ( x ) f_X(x) fX(x)
连续性随机变量的概密与分布函数
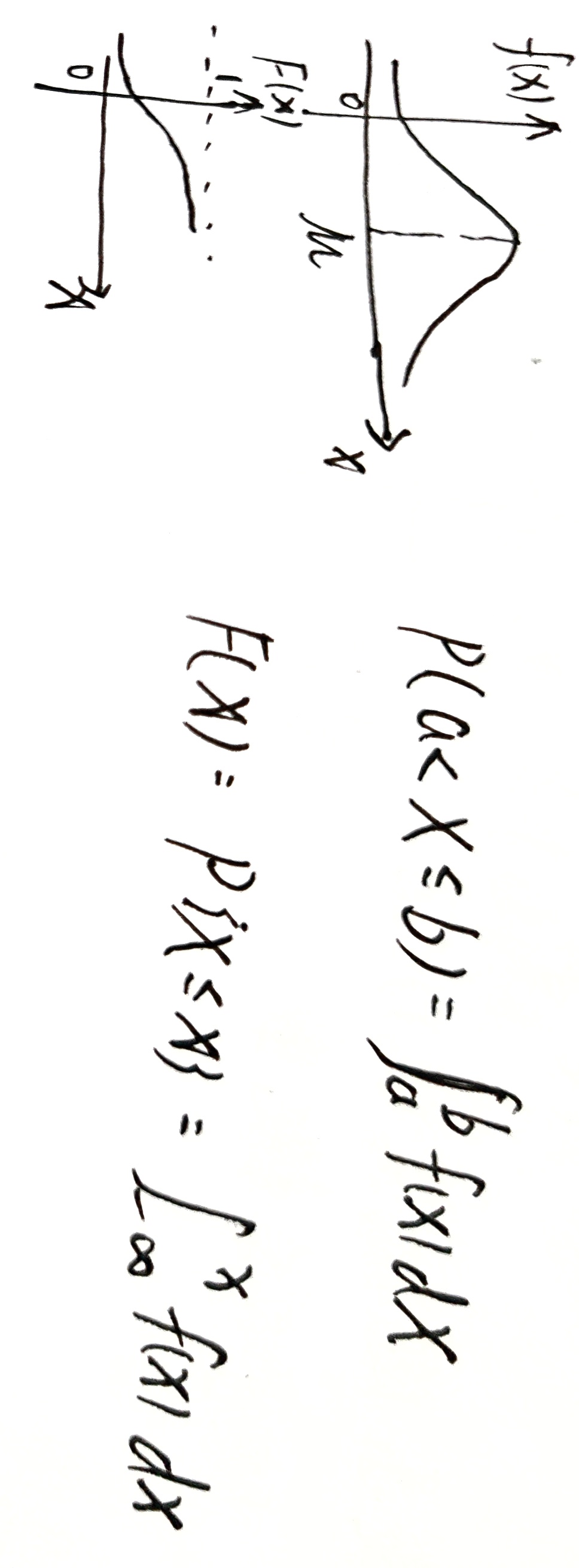
概率密度函数体现的并非连续随机变量的真实概率,而是不同取值可能性之间的相对关系。
对连续型随机变量来说,其可能取值的数目为不可列无限个,当归一化的概率被分配到这无限个点上时,每个点的概率都是一个无穷小量,取极限的话就等于零。
概率密度函数的作用就是对这些无穷小量加以区分,无穷小量之间是有相对大小的( 1 x , 2 x \frac{1}{x},\frac{2}{x} x1,x2 在 x → ∞ x\rightarrow \infty x→∞ 时都是无穷小,但后者是前者的两倍),由概率密度函数刻画。
概密表示概率
已知概率密度函数 f ( x ) f(x) f(x) ,随机变量 X X X 在 ( a , b ] (a,b] (a,b] 上的概率可表示为 P ( a < X ≤ b ) = ∫ a b f ( x ) d x P(a<X\le b)=\int_{a}^bf(x)dx P(a<X≤b)=∫abf(x)dx
简单随机抽样
样本
{
①
x
1
,
x
2
,
⋯
,
x
n
是相互独立的随机变量
②
x
1
,
x
x
,
⋯
,
x
n
与总体
X
同分布
样本\left\{ \begin{aligned} ①&\quad x_1,x_2,\cdots,x_n是相互独立的随机变量\\ ②&\quad x_1,x_x,\cdots,x_n与总体X同分布 \end{aligned} \right.
样本{①②x1,x2,⋯,xn是相互独立的随机变量x1,xx,⋯,xn与总体X同分布
在ML中,可将
x
1
,
x
2
,
⋯
,
x
n
x_1,x_2,\cdots,x_n
x1,x2,⋯,xn 看作不同维度上的变量
- 联合分布函数 F ( x 1 , x 2 , ⋯ , x n ) = ∏ i = 1 n F ( x i ) F(x_1,x_2,\cdots,x_n)=\prod\limits_{i=1}^n F(x_i) F(x1,x2,⋯,xn)=i=1∏nF(xi)
- 联合概率密度 f ( x 1 , x 2 , ⋯ , x n ) = ∏ i = 1 n f ( x i ) f(x_1,x_2,\cdots,x_n)=\prod\limits_{i=1}^nf(x_i) f(x1,x2,⋯,xn)=i=1∏nf(xi)
3.2.3 概率公理
非负性: P ( A ) ≥ 0 P(A)\ge 0 P(A)≥0
加法公式:
- p ( A ⋃ B ) = p ( A ) + p ( B ) − p ( A B ) p(A\bigcup B)=p(A)+p(B)-p(AB) p(A⋃B)=p(A)+p(B)−p(AB)
- p ( A ⋃ B ⋃ C ) = p ( A ) + p ( B ) + p ( C ) − p ( A B ) − p ( A C ) − p ( B C ) + p ( A B C ) p(A\bigcup B\bigcup C)=p(A)+p(B)+p(C)-p(AB)-p(AC)-p(BC)+p(ABC) p(A⋃B⋃C)=p(A)+p(B)+p(C)−p(AB)−p(AC)−p(BC)+p(ABC)
正则性: p ( Ω ) = 1 p(\Omega)=1 p(Ω)=1
3.3 二维随机变量
3.3.1 联合函数
( X , Y ) (X,Y) (X,Y) 为二维变量,表示一个事件由两个维度决定
F ( x , y ) = P ( X ≤ x ⋂ Y ≤ y ) F(x,y)=P(X\le x\bigcap Y\le y) F(x,y)=P(X≤x⋂Y≤y) ,表示随机点 ( X , Y ) (X,Y) (X,Y) 位于 ( x , y ) (x,y) (x,y) 左下方的概率
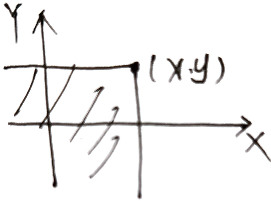
性质
-
F ( x , y ) F(x,y) F(x,y) 分别关于X,Y单调不减
-
0 ≤ F ( x , y ) ≤ 1 { F ( − ∞ , 0 ) = 0 F ( − ∞ , + ∞ ) = 1 F ( 0 , − ∞ ) = 0 F ( − ∞ , − ∞ ) = 0 0\le F(x,y)\le 1\left\{\begin{aligned}F(-\infty,0)=0&&F(-\infty,+\infty)=1\\F(0,-\infty)=0&&F(-\infty,-\infty)=0\end{aligned}\right. 0≤F(x,y)≤1{F(−∞,0)=0F(0,−∞)=0F(−∞,+∞)=1F(−∞,−∞)=0
-
F ( x , y ) F(x,y) F(x,y) 关于 X , Y X,Y X,Y 右连续
-
∀ x 1 ≤ x 2 , y 1 ≤ y 2 \forall x_1\le x_2,y_1\le y_2 ∀x1≤x2,y1≤y2 , P { x 1 < X ≤ x 2 , y 1 < Y ≤ y 2 } = F ( x 2 , y 2 ) − F ( x 1 , y 2 ) − F ( x 2 , y 1 ) + F ( x 1 , y 1 ) P\left\{x_1< X\le x_2,y_1<Y\le y_2 \right\}=F(x_2,y_2)-F(x_1,y_2)-F(x_2,y_1)+F(x_1,y_1) P{x1<X≤x2,y1<Y≤y2}=F(x2,y2)−F(x1,y2)−F(x2,y1)+F(x1,y1)
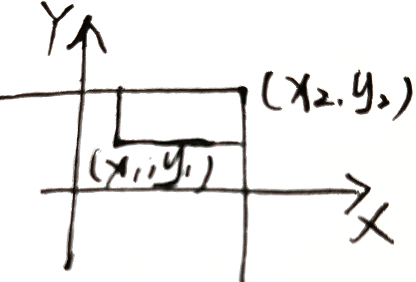
3.3.2 二维离散型随机变量 (x,y)
有限对 ( X , Y ) (X,Y) (X,Y) :研究 ( x , y ) (x,y) (x,y) 同时取定这一事件发生的概率
联合概率分布
X
\
Y
y
1
y
2
⋯
y
n
x
1
p
11
p
12
⋯
p
1
n
x
2
p
21
p
22
⋯
p
2
n
⋮
⋮
⋮
⋱
⋮
x
n
p
n
1
p
n
2
⋯
p
n
n
\begin{array}{c|lcr} X\backslash Y&y_1&y_2&\cdots&y_n\\ \hline x_1&p_{11}&p_{12}&\cdots&p_{1n}\\ x_2&p_{21}&p_{22}&\cdots&p_{2n}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ x_n&p_{n1}&p_{n2}&\cdots&p_{nn} \end{array}
X\Yx1x2⋮xny1p11p21⋮pn1y2p12p22⋮pn2⋯⋯⋯⋱⋯ynp1np2n⋮pnn
p
i
j
≥
0
p_{ij}\ge 0
pij≥0 ,
∑
i
=
1
∞
∑
j
=
1
∞
p
i
j
=
1
\sum\limits_{i=1}^\infty\sum\limits_{j=1}^\infty p_{ij}=1
i=1∑∞j=1∑∞pij=1
eg:
X = 1 , 2 , 3 , 4 X=1,2,3,4 X=1,2,3,4 , Y = 1 , 2 , ⋯ , X Y=1,2,\cdots,X Y=1,2,⋯,X ,求 ( x , y ) (x,y) (x,y) 的联合概率分布
( X = i , Y = j ) (X=i,Y=j) (X=i,Y=j) , i = 1 , 2 , 3 , 4 i=1,2,3,4 i=1,2,3,4 , y ≤ X , y = 1 , 2 , ⋯ , i y\le X,y=1,2,\cdots,i y≤X,y=1,2,⋯,i
P
(
X
=
i
,
Y
=
j
)
=
P
(
X
=
i
)
P
(
Y
=
j
∣
X
=
i
)
=
1
4
1
i
P(X=i,Y=j)=P(X=i)P(Y=j\mid X=i)=\frac{1}{4}\frac{1}{i}
P(X=i,Y=j)=P(X=i)P(Y=j∣X=i)=41i1
x
\
y
1
2
3
4
1
1
4
1
8
1
12
1
16
2
0
1
8
1
12
1
16
3
0
0
1
12
1
16
4
0
0
0
1
16
\begin{array}{c|cccc} x\backslash y&1&2&3&4\\ \hline 1&\frac{1}{4}&\frac{1}{8}&\frac{1}{12}&\frac{1}{16}\\ 2&0&\frac{1}{8}&\frac{1}{12}&\frac{1}{16}\\ 3&0&0&\frac{1}{12}&\frac{1}{16}\\ 4&0&0&0&\frac{1}{16}\\ \end{array}
x\y12341410002818100312112112104161161161161
3.3.3 二维连续型随机变量
研究 ( X , Y ) (X,Y) (X,Y) 位于某一范围这一事件发生的概率
概率密度
f ( x , y ) ≥ 0 f(x,y)\ge 0 f(x,y)≥0 ,对于 ∀ ( x , y ) \forall (x,y) ∀(x,y) ,有二维随机变量的分布函数 F ( x , y ) = ∫ − ∞ x ∫ − ∞ y f ( u , v ) d u d v F(x,y)=\int_{-\infty}^x\int_{-\infty}^yf(u,v)dudv F(x,y)=∫−∞x∫−∞yf(u,v)dudv
P { ( x , y ) ∈ G } = ∬ G f ( x , y ) d x d y P\{(x,y)\in G\}=\iint\limits_{G} f(x,y)dxdy P{(x,y)∈G}=G∬f(x,y)dxdy
- P { ( x , y ) ∈ G } = ∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) d x d y = 1 P\{(x,y)\in G\}=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} f(x,y)dxdy=1 P{(x,y)∈G}=∫−∞+∞∫−∞+∞f(x,y)dxdy=1
eg:
( X , Y ) (X,Y) (X,Y) ,有 f ( x , y ) = { k e − ( 2 x + 3 y ) , x > 0 , y > 0 0 , 其他 f(x,y)=\begin{cases}ke^{-(2x+3y)}&,x>0,y>0\\0&,其他\end{cases} f(x,y)={ke−(2x+3y)0,x>0,y>0,其他
(1) 求参数k
∫ 0 + ∞ ∫ 0 + ∞ f ( x , y ) d x d y = 1 = k ∫ 0 + ∞ e − 2 x d x ∫ 0 + ∞ e − 3 y d y = k 6 e − 2 x ∣ 0 + ∞ ⋅ e − 3 y ∣ 0 + ∞ = k 6 ⇒ k = 6 \int_{0}^{+\infty}\int_{0}^{+\infty}f(x,y)dxdy=1=k\int_{0}^{+\infty}e^{-2x}dx\int_{0}^{+\infty} e^{-3y}dy=\frac{k}{6}e^{-2x}\mid_{0}^{+\infty}\cdot e^{-3y}\mid_{0}^{+\infty}=\frac{k}{6}\Rightarrow k=6 ∫0+∞∫0+∞f(x,y)dxdy=1=k∫0+∞e−2xdx∫0+∞e−3ydy=6ke−2x∣0+∞⋅e−3y∣0+∞=6k⇒k=6
(2) 求分布函数
F
(
x
,
y
)
F(x,y)
F(x,y)
F
(
x
,
y
)
=
{
∫
0
x
∫
0
y
f
(
x
,
y
)
d
x
d
y
,
x
>
0
,
y
>
0
0
,
其他
=
{
∫
0
x
2
e
−
2
x
d
x
∫
0
y
3
e
−
3
y
d
y
,
x
>
0
,
y
>
0
0
,
其他
=
{
2
e
−
2
x
∣
0
x
e
−
3
y
d
y
∣
0
y
,
x
>
0
,
y
>
0
0
,
其他
=
(
e
−
2
x
−
1
)
(
e
−
3
y
−
1
)
\begin{aligned} F(x,y)&=\begin{cases} \int_{0}^{x}\int_{0}^{y}f(x,y)dxdy&,x>0,y>0\\ 0&,其他 \end{cases}\\ &=\begin{cases} \int_{0}^{x}2e^{-2x}dx \int_{0}^{y}3e^{-3y}dy&,x>0,y>0\\ 0&,其他 \end{cases}\\ &=\begin{cases} 2e^{-2x}\mid_{0}^x e^{-3y}dy\mid_{0}^y&,x>0,y>0\\ 0&,其他 \end{cases}\\ &=(e^{-2x}-1)(e^{-3y}-1) \end{aligned}
F(x,y)={∫0x∫0yf(x,y)dxdy0,x>0,y>0,其他={∫0x2e−2xdx∫0y3e−3ydy0,x>0,y>0,其他={2e−2x∣0xe−3ydy∣0y0,x>0,y>0,其他=(e−2x−1)(e−3y−1)
(3) 求
P
(
Y
≤
X
)
P(Y\le X)
P(Y≤X) 的概率
P
{
Y
≤
X
}
=
∫
0
+
∞
d
x
∫
0
x
f
(
x
,
y
)
d
y
=
∫
0
+
∞
d
x
∫
0
x
6
e
−
2
x
e
−
3
y
d
y
=
∫
0
+
∞
(
−
2
)
e
−
2
x
d
x
∫
0
x
(
−
3
y
)
e
−
3
y
d
y
=
∫
0
+
∞
(
−
2
)
e
−
2
x
⋅
e
−
3
y
∣
0
x
d
x
=
−
2
∫
0
+
∞
(
e
−
5
x
−
e
−
2
x
)
d
x
=
3
5
\begin{aligned} P\{Y\le X\}&=\int_{0}^{+\infty}dx\int_{0}^xf(x,y)dy\\ &=\int_{0}^{+\infty}dx\int_{0}^x6e^{-2x}e^{-3y}dy\\ &=\int_{0}^{+\infty}(-2)e^{-2x}dx\int_{0}^x(-3y)e^{-3y}dy=\int_{0}^{+\infty}(-2)e^{-2x}\cdot e^{-3y}\mid_{0}^xdx\\ &=-2\int_{0}^{+\infty}(e^{-5x}-e^{-2x})dx=\frac{3}{5} \end{aligned}
P{Y≤X}=∫0+∞dx∫0xf(x,y)dy=∫0+∞dx∫0x6e−2xe−3ydy=∫0+∞(−2)e−2xdx∫0x(−3y)e−3ydy=∫0+∞(−2)e−2x⋅e−3y∣0xdx=−2∫0+∞(e−5x−e−2x)dx=53
3.3.4 边缘分布
二维随机变量 ( X , Y ) (X,Y) (X,Y) 有整体分布函数 F ( x , y ) F(x,y) F(x,y) , X , Y X,Y X,Y 都是随机变量—— F X ( X ) , F Y ( y ) F_X(X),F_Y(y) FX(X),FY(y)
令 y → ∞ y\rightarrow \infty y→∞ ,则 F ( x , y ) → F X ( x ) F(x,y)\rightarrow F_X(x) F(x,y)→FX(x)
-
F X ( x ) = P ( X ≤ x ) = P { X ≤ x , Y < + ∞ } = F ( x , + ∞ ) F_X(x)=P(X\le x)=P\{X\le x,Y<+\infty\}=F(x,+\infty) FX(x)=P(X≤x)=P{X≤x,Y<+∞}=F(x,+∞)
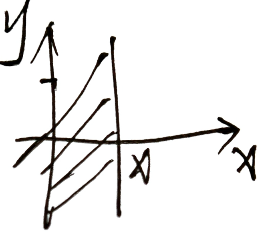
令 x → ∞ x\rightarrow \infty x→∞ ,则 F ( x , y ) → F Y ( y ) F(x,y)\rightarrow F_Y(y) F(x,y)→FY(y)
-
F Y ( y ) = P ( Y ≤ y ) = P { X < + ∞ , Y ≤ y } = F ( + ∞ , y ) F_Y(y)=P(Y\le y)=P\{X< +\infty,Y\le y\}=F(+\infty,y) FY(y)=P(Y≤y)=P{X<+∞,Y≤y}=F(+∞,y)

离散型
分布律 P { X = x , Y = y } = p i j , i , j = 1 , 2 , ⋯ P\{X=x,Y=y\}=p_{ij},i,j=1,2,\cdots P{X=x,Y=y}=pij,i,j=1,2,⋯
- X边缘分布: P { X = x i } = P { X ≤ x i , y < + ∞ } = ∑ j = 1 + ∞ p i j = Δ p i , i = 1 , 2 , ⋯ P\{X=x_i\}=P\{X\le x_i,y<+\infty\}=\sum\limits_{j=1}^{+\infty}p_{ij}\overset{\Delta}{=}p_i,i=1,2,\cdots P{X=xi}=P{X≤xi,y<+∞}=j=1∑+∞pij=Δpi,i=1,2,⋯
- Y边缘分布: P { Y = y i } = P { x < + ∞ , Y ≤ y i } = ∑ i = 1 + ∞ p i j = Δ p j , j = 1 , 2 , ⋯ P\{Y=y_i\}=P\{x<+\infty,Y\le y_i\}=\sum\limits_{i=1}^{+\infty}p_{ij}\overset{\Delta}{=}p_j,j=1,2,\cdots P{Y=yi}=P{x<+∞,Y≤yi}=i=1∑+∞pij=Δpj,j=1,2,⋯
eg:
x
\
y
0
10
20
0
0.35
0.04
0.025
1
0.025
0.15
0.04
2
0.02
0.1
0.25
\begin{array}{c|ccc} x\backslash y&0&10&20\\ \hline 0&0.35&0.04&0.025\\ 1&0.025&0.15&0.04\\ 2&0.02&0.1&0.25 \end{array}
x\y01200.350.0250.02100.040.150.1200.0250.040.25
X,Y边缘分布
X
0
0.415
1
0.215
2
0.37
Y
0
0.395
10
0.215
20
0.315
\begin{array}{c|c} X&\\ \hline 0&0.415\\ 1&0.215\\ 2&0.37 \end{array}\qquad \begin{array}{c|c} Y&\\ \hline 0&0.395\\ 10&0.215\\ 20&0.315 \end{array}\\
X0120.4150.2150.37Y010200.3950.2150.315
P
(
X
=
2
∣
Y
=
20
)
=
P
(
X
=
2
,
Y
=
20
)
P
(
Y
=
20
)
=
0.25
0.315
P(X=2\vert Y=20)=\frac{P(X=2,Y=20)}{P(Y=20)}=\frac{0.25}{0.315}
P(X=2∣Y=20)=P(Y=20)P(X=2,Y=20)=0.3150.25
连续型
对于 ( X , Y ) (X,Y) (X,Y) 有概率密度 ( x , y ) (x,y) (x,y) ,及其联合分布函数 F ( x , y ) F(x,y) F(x,y)
f X ( x ) = ∫ − ∞ + ∞ f ( x , y ) d y f_X(x)=\int_{-\infty}^{+\infty}f(x,y)dy fX(x)=∫−∞+∞f(x,y)dy , f Y ( y ) = ∫ − ∞ + ∞ f ( x , y ) d x f_Y(y)=\int_{-\infty}^{+\infty}f(x,y)dx fY(y)=∫−∞+∞f(x,y)dx
F X ( x ) = F ( x , + ∞ ) = ∫ − ∞ x ∫ − ∞ + ∞ f ( x , y ) d x d y = ∫ − ∞ x ∫ − ∞ + ∞ f ( x , y ) d y d x = ∫ − ∞ x f X ( x , y ) d x F_X(x)=F(x,+\infty)=\int_{-\infty}^x\int_{-\infty}^{+\infty}f(x,y)dxdy=\int_{-\infty}^x\int_{-\infty}^{+\infty}f(x,y)dydx=\int_{-\infty}^xf_X(x,y)dx FX(x)=F(x,+∞)=∫−∞x∫−∞+∞f(x,y)dxdy=∫−∞x∫−∞+∞f(x,y)dydx=∫−∞xfX(x,y)dx
F Y ( y ) = F ( + ∞ , y ) = ∫ − ∞ y ∫ − ∞ + ∞ f ( x , y ) d x d y = ∫ − ∞ y ∫ − ∞ + ∞ f ( x , y ) d x d y = ∫ − ∞ y f Y ( x , y ) d y F_Y(y)=F(+\infty,y)=\int_{-\infty}^y\int_{-\infty}^{+\infty}f(x,y)dxdy=\int_{-\infty}^y\int_{-\infty}^{+\infty}f(x,y)dxdy=\int_{-\infty}^yf_Y(x,y)dy FY(y)=F(+∞,y)=∫−∞y∫−∞+∞f(x,y)dxdy=∫−∞y∫−∞+∞f(x,y)dxdy=∫−∞yfY(x,y)dy
eg:
f ( x , y ) = { 6 , x 2 ≤ y < x 0 , 其他 f(x,y)=\begin{cases}6&,x^2\le y<x\\0&,其他\end{cases} f(x,y)={60,x2≤y<x,其他

f X ( x ) = { ∫ − ∞ + ∞ f ( x , y ) d y , 0 ≤ x ≤ 1 0 , 其他 = { ∫ x 2 x 6 d y , 0 ≤ x ≤ 1 0 , 其他 = { 6 ( x − x 2 ) , 0 ≤ x ≤ 1 0 , 其他 f_X(x)=\begin{cases} \int_{-\infty}^{+\infty}f(x,y)dy&,0\le x\le 1\\ 0&,其他 \end{cases} =\begin{cases} \int_{x^2}^{x}6dy&,0\le x\le 1\\ 0&,其他 \end{cases}= \begin{cases} 6(x-x^2)&,0\le x\le 1\\ 0&,其他 \end{cases} fX(x)={∫−∞+∞f(x,y)dy0,0≤x≤1,其他={∫x2x6dy0,0≤x≤1,其他={6(x−x2)0,0≤x≤1,其他
f Y ( y ) = { ∫ − ∞ + ∞ f ( x , y ) d x , 0 ≤ y ≤ 1 0 , 其他 = { ∫ y y 6 d y , 0 ≤ y ≤ 1 0 , 其他 = { 6 ( y − y ) d y , 0 ≤ y ≤ 1 0 , 其他 f_Y(y)=\begin{cases} \int_{-\infty}^{+\infty}f(x,y)dx&,0\le y\le 1\\ 0&,其他 \end{cases} =\begin{cases} \int_{y}^{\sqrt{y}}6dy&,0\le y\le 1\\ 0&,其他 \end{cases}= \begin{cases} 6(\sqrt{y}-y)dy&,0\le y\le 1\\ 0&,其他 \end{cases} fY(y)={∫−∞+∞f(x,y)dx0,0≤y≤1,其他={∫yy6dy0,0≤y≤1,其他={6(y−y)dy0,0≤y≤1,其他
3.4 数据的数字特征
3.4.1 数学期望
反映数据平均水平
离散型期望
{ P ( X = x k ) = p k , k = 1 , 2 , ⋯ E X = ∑ k = 1 n x k p k \left\{ \begin{aligned} &P(X=x_k)=p_k,k=1,2,\cdots\\ &EX=\sum\limits_{k=1}^nx_kp_k \end{aligned} \right. ⎩ ⎨ ⎧P(X=xk)=pk,k=1,2,⋯EX=k=1∑nxkpk
连续型随机变量
X ∼ f ( x ) = { 1 b − a , a < x < b 0 , 其他 X\sim f(x)=\begin{cases}\frac{1}{b-a}&,a<x<b\\0&,其他\end{cases} X∼f(x)={b−a10,a<x<b,其他
E X = ∫ − ∞ + ∞ x f ( x ) d x = ∫ a b x b − a d x = a + b 2 EX=\int_{-\infty}^{+\infty}xf(x)dx=\int_a^b\frac{x}{b-a}dx=\frac{a+b}{2} EX=∫−∞+∞xf(x)dx=∫abb−axdx=2a+b
二维离散型
( X , Y ) ∼ P { X = x i , Y = y i } = p i j , i = 1 , 2 , ⋯ (X,Y)\sim P\{X=x_i,Y=y_i\}=p_{ij},i=1,2,\cdots (X,Y)∼P{X=xi,Y=yi}=pij,i=1,2,⋯ ,求 Z = g ( X , Y ) Z=g(X,Y) Z=g(X,Y)
变量函数,将两个值映射为一个值
x,y取定不同的值,有不同的结果
函数期望 E Z = E [ g ( x , y ) ] = ∑ i = 1 ∞ ∑ j = 1 ∞ [ g ( x i , y j ) p i j ] EZ=E[g(x,y)]=\sum\limits_{i=1}^{\infty}\sum\limits_{j=1}^{\infty}[g(x_i,y_j)p_{ij}] EZ=E[g(x,y)]=i=1∑∞j=1∑∞[g(xi,yj)pij]
eg:
X
\
Y
0
1
2
0
0.1
0.25
0.15
1
0.15
0.2
0.15
\begin{array}{c|ccc} X\backslash Y&0&1&2\\ \hline 0&0.1&0.25&0.15\\ 1&0.15&0.2&0.15 \end{array}
X\Y0100.10.1510.250.220.150.15
求
Z
=
s
i
n
π
(
X
+
Y
)
2
Z=sin\frac{\pi(X+Y)}{2}
Z=sin2π(X+Y)
E
Z
=
E
[
s
i
n
π
(
x
+
y
)
2
]
=
s
i
n
0
+
0
2
π
⋅
0.1
+
s
i
n
0
+
1
2
π
⋅
0.25
+
s
i
n
0
+
2
2
π
⋅
0.15
+
s
i
n
1
+
0
2
π
⋅
0.15
+
s
i
n
1
+
1
2
π
⋅
0.2
+
s
i
n
1
+
2
2
π
⋅
0.15
=
0.25
EZ=E\left[sin\frac{\pi(x+y)}{2}\right]=sin\frac{0+0}{2}\pi\cdot 0.1+sin\frac{0+1}{2}\pi\cdot 0.25+sin\frac{0+2}{2}\pi\cdot0.15\\+sin\frac{1+0}{2}\pi\cdot 0.15+sin\frac{1+1}{2}\pi\cdot 0.2+sin\frac{1+2}{2}\pi\cdot0.15=0.25
EZ=E[sin2π(x+y)]=sin20+0π⋅0.1+sin20+1π⋅0.25+sin20+2π⋅0.15+sin21+0π⋅0.15+sin21+1π⋅0.2+sin21+2π⋅0.15=0.25
二维连续型随机变量
( X , Y ) (X,Y) (X,Y) 连续型变量函数 Z = g ( X , Y ) Z=g(X,Y) Z=g(X,Y) , E Z = E [ g ( x , y ) ] = ∫ − ∞ + ∞ ∫ − ∞ + ∞ g ( x , y ) f ( x , y ) d x d y EZ=E\left[g(x,y)\right]=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g(x,y)f(x,y)dxdy EZ=E[g(x,y)]=∫−∞+∞∫−∞+∞g(x,y)f(x,y)dxdy
eg:
f
(
x
,
y
)
=
{
3
2
x
3
y
2
,
1
x
1
0
,
其他
,求
E
Y
f(x,y)=\begin{cases}\frac{3}{2x^3y^2}&,\frac{1}{x}1\\0&,其他\end{cases},求EY
f(x,y)={2x3y230,x11,其他,求EY
E Y = ∫ − ∞ + ∞ ∫ − ∞ + ∞ y f ( x , y ) d x d y = ∫ 1 + ∞ d x ∫ 1 x x 3 y 2 x 3 y 2 d y = ∫ 1 + ∞ 3 2 x 3 l n y ∣ 1 / x x d x = 3 2 ∫ 1 + ∞ l n x x 3 d x = 3 2 ∫ 1 + ∞ l n x d ( − 1 x 2 ) = 3 4 \begin{aligned} EY&=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}yf(x,y)dxdy=\int_1^{+\infty}dx\int_{\frac{1}{x}}^x\frac{3y}{2x^3y^2}dy=\int_{1}^{+\infty}\frac{3}{2x^3}lny\vert_{1/ x}^xdx\\ &=\frac{3}{2}\int_{1}^{+\infty}\frac{lnx}{x^3}dx=\frac{3}{2}\int_{1}^{+\infty}lnxd\left(-\frac{1}{x^2}\right)=\frac{3}{4} \end{aligned} EY=∫−∞+∞∫−∞+∞yf(x,y)dxdy=∫1+∞dx∫x1x2x3y23ydy=∫1+∞2x33lny∣1/xxdx=23∫1+∞x3lnxdx=23∫1+∞lnxd(−x21)=43
期望性质
- E ( C ) = C E(C)=C E(C)=C
- E ( C X ) = C E X E(CX)=CEX E(CX)=CEX
- E ( a X + b Y + C ) = a E X + b E Y + C E(aX+bY+C)=aEX+bEY+C E(aX+bY+C)=aEX+bEY+C
- X , Y X,Y X,Y 相互独立,则有 E ( X ⋅ Y ) = E X ⋅ E Y E(X\cdot Y)=EX\cdot EY E(X⋅Y)=EX⋅EY
eg:性质求期望
20个人,10个站,无人下车则车不停,X表示停车次数,求EX
设 { 0 , 第 i 站无人下车 1 , 第 i 站有人下车 , i = 1 , 2 , ⋯ , 10 \begin{cases}0&,第i站无人下车\\1&,第i站有人下车\end{cases},i=1,2,\cdots,10 {01,第i站无人下车,第i站有人下车,i=1,2,⋯,10
第 i i i 站有人下车 ⟺ \iff ⟺ 1-其他站全下完车 P { X i = 1 } = 1 − ( 9 10 ) 20 P\{X_i=1\}=1-\left(\frac{9}{10}\right)^{20} P{Xi=1}=1−(109)20 第 i i i 站有人下车的期望是 E X i = x i p i = 1 − ( 9 10 ) 20 EX_i=x_i p_i=1-\left(\frac{9}{10}\right)^{20} EXi=xipi=1−(109)20
E X = E ( X 1 + X 2 + ⋯ + X 10 ) = 10 × [ 1 − ( 9 10 ) 20 ] EX=E(X_1+X_2+\cdots+X_{10})=10\times\left[1-\left(\frac{9}{10}\right)^{20}\right] EX=E(X1+X2+⋯+X10)=10×[1−(109)20]
3.4.2 方差
反映数据分散程度
D X = E ( X − E X ) 2 = E [ X 2 + ( E X ) 2 − 2 X E X ] = E X 2 + ( E X ) 2 − 2 ( E X ) 2 = E X 2 − ( E X ) 2 = S 2 ( 标准差平方 ) DX=E(X-EX)^2=E[X^2+(EX)^2-2XEX]=EX^2+(EX)^2-2(EX)^2=EX^2-(EX)^2=S^2(标准差平方) DX=E(X−EX)2=E[X2+(EX)2−2XEX]=EX2+(EX)2−2(EX)2=EX2−(EX)2=S2(标准差平方)
随机变量与期望距离的平方的期望
3.4.3 协方差
描述两个随机变量之间的相互关系,就需要用到协方差和相关系数——描述两个随机变量之间的线性关系
协方差 度量了两个随机变量之间的线性关系,即变量 Y Y Y 能否表示成以另一变量 X X X 为自变量的 a X + b aX+b aX+b 形式
C o v ( X , Y ) = E [ ( X − E X ) ( Y − E Y ) ] = E ( X Y ) − E X ⋅ E Y { = 0 , X 与 Y 相互独立 > 0 , 正相关 < 0 , 负相关 Cov(X,Y)=E[(X-EX)(Y-EY)]=E(XY)-EX\cdot EY\begin{cases}=0,X与Y相互独立\\>0,正相关\\<0,负相关\end{cases} Cov(X,Y)=E[(X−EX)(Y−EY)]=E(XY)−EX⋅EY⎩ ⎨ ⎧=0,X与Y相互独立>0,正相关<0,负相关
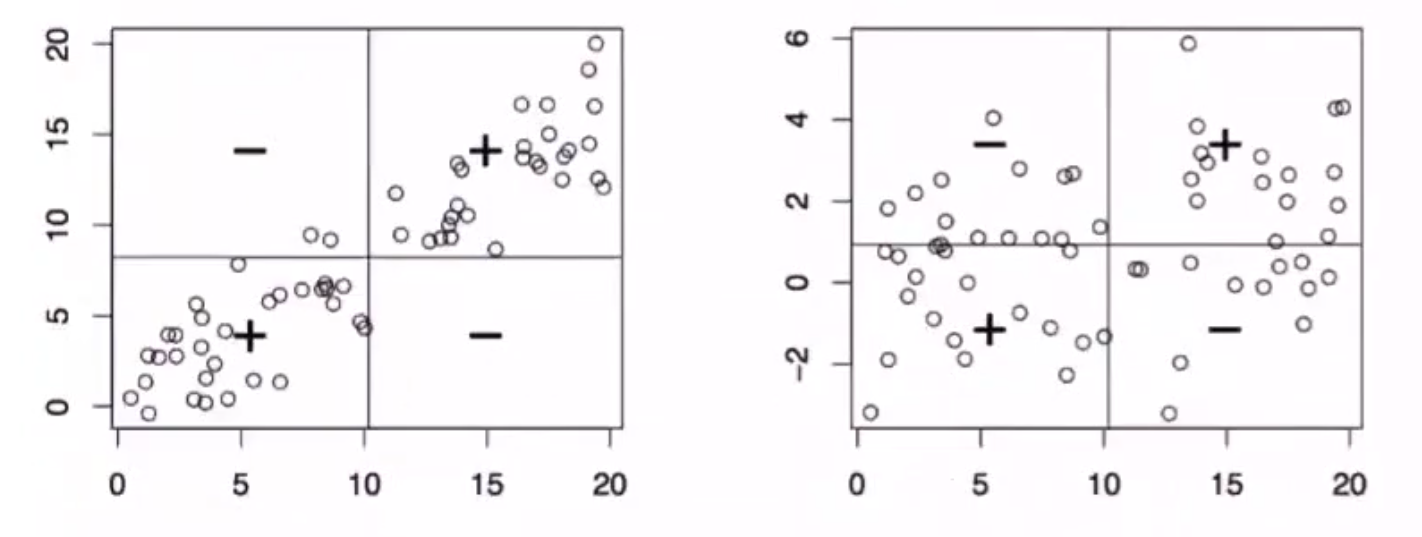
X , Y 相互独立 ⇒ C o v ( X , Y ) ≈ 0 X,Y相互独立\Rightarrow Cov(X,Y)\approx 0 X,Y相互独立⇒Cov(X,Y)≈0
相关系数
根据协方差可以进一步求出相关系数,相关系数是绝对值不大于1的常数
- 等于1意味着两者满足完全正相关;
- 等于-1意味着两者满足完全负相关
- 等于0意味着两者不相关
3.5 随机变量的分布
3.5.1 均匀分布
X ∼ U ( a , b ) X\sim U(a,b) X∼U(a,b) ,每一件事出现的可能性相等
f ( x ) = 1 b − a , a ≤ x ≤ b f(x)=\frac{1}{b-a},a\le x\le b f(x)=b−a1,a≤x≤b
- E X = a + b 2 EX=\frac{a+b}{2} EX=2a+b
- D X = ( a − b ) 2 12 DX=\frac{(a-b)^2}{12} DX=12(a−b)2
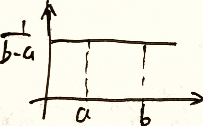
3.5.2 伯努利实验
一次随机实验,只出现两种结果
A A A 事件 p p p , A ‾ \overline{A} A 事件 q = 1 − p q=1-p q=1−p
f ( k ; p ) = { p , k = 1 1 − p , k = 0 f(k;p)=\begin{cases}p&,k=1\\1-p&,k=0\end{cases} f(k;p)={p1−p,k=1,k=0
- E X = p EX=p EX=p
- D X = E X 2 − ( E X ) 2 = p − p 2 = p ( 1 − p ) = p q DX=EX^2-(EX)^2=p-p^2=p(1-p)=pq DX=EX2−(EX)2=p−p2=p(1−p)=pq
3.5.3 二项分布
n n n 重伯努利实验 X ∼ B ( n , p ) X\sim B(n,p) X∼B(n,p)
- n n n 次实验独立
- 每次实验只有两种结果 A A A 和 A ‾ \overline{A} A
- 每次实验 A A A 出现的概率都不变
P { X = k } = C n k p k ( 1 − p ) n − k = ( n k ) p k ( 1 − p ) n − k = P ( X ∣ n , p ) , k = 0 , 1 , ⋯ , n P\{X=k\}=C_n^kp^k(1-p)^{n-k}=\left(\begin{aligned}n\\k\end{aligned}\right)p^k(1-p)^{n-k}=P(X\vert n,p),k=0,1,\cdots,n P{X=k}=Cnkpk(1−p)n−k=(nk)pk(1−p)n−k=P(X∣n,p),k=0,1,⋯,n
∑ k = 0 n ( n k ) p k ( 1 − p ) n − k = 1 \sum\limits_{k=0}^n\left(\begin{aligned}n\\k\end{aligned}\right)p^k(1-p)^{n-k}=1 k=0∑n(nk)pk(1−p)n−k=1
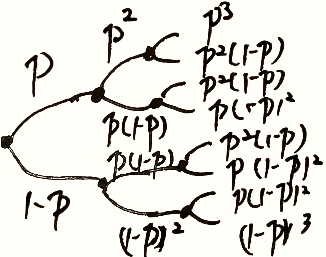
- 最后结果是每次选择的累计量
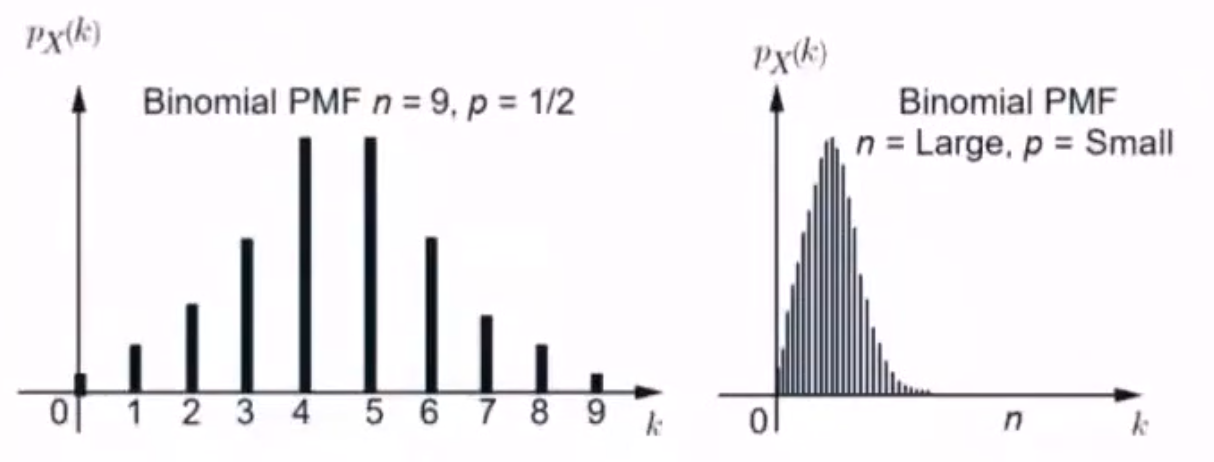
- E X = n p EX=np EX=np
- D X = n p q DX=npq DX=npq
3.5.4 多项式分布
二项式 ( x + y ) n = ∑ k = 0 n ( n k ) x k y n − k = ∑ k = 0 n ( n k ) y k x n − k (x+y)^n=\sum\limits_{k=0}^n \left(\begin{aligned}n\\k\end{aligned}\right)x^ky^{n-k}=\sum\limits_{k=0}^n \left(\begin{aligned}n\\k\end{aligned}\right)y^kx^{n-k} (x+y)n=k=0∑n(nk)xkyn−k=k=0∑n(nk)ykxn−k

多项式概密
f
(
X
=
x
1
,
X
=
x
2
,
⋯
,
X
=
x
k
)
=
{
n
!
x
1
!
x
2
!
⋯
x
k
!
p
1
x
1
p
2
x
2
⋯
p
k
x
k
,
∑
i
=
0
k
x
i
=
n
0
,其他
=
Γ
(
∑
X
i
+
1
)
∏
[
Γ
(
∑
X
i
+
1
)
]
∏
i
=
1
k
p
i
x
i
\begin{aligned} f(X=x_1,X=x_2,\cdots,X=x_k)&=\begin{cases}\frac{n!}{x_1!x_2!\cdots x_k!}p_1^{x_1}p_2^{x_2}\cdots p_k^{x_k}&,\sum\limits_{i=0}^k x_i=n\\0&,其他\end{cases}\\ &=\frac{\Gamma(\sum X_i+1)}{\prod[\Gamma(\sum X_i+1)]}\prod\limits_{i=1}^kp_i^{x_i} \end{aligned}
f(X=x1,X=x2,⋯,X=xk)=⎩
⎨
⎧x1!x2!⋯xk!n!p1x1p2x2⋯pkxk0,i=0∑kxi=n,其他=∏[Γ(∑Xi+1)]Γ(∑Xi+1)i=1∏kpixi
-
伽马函数
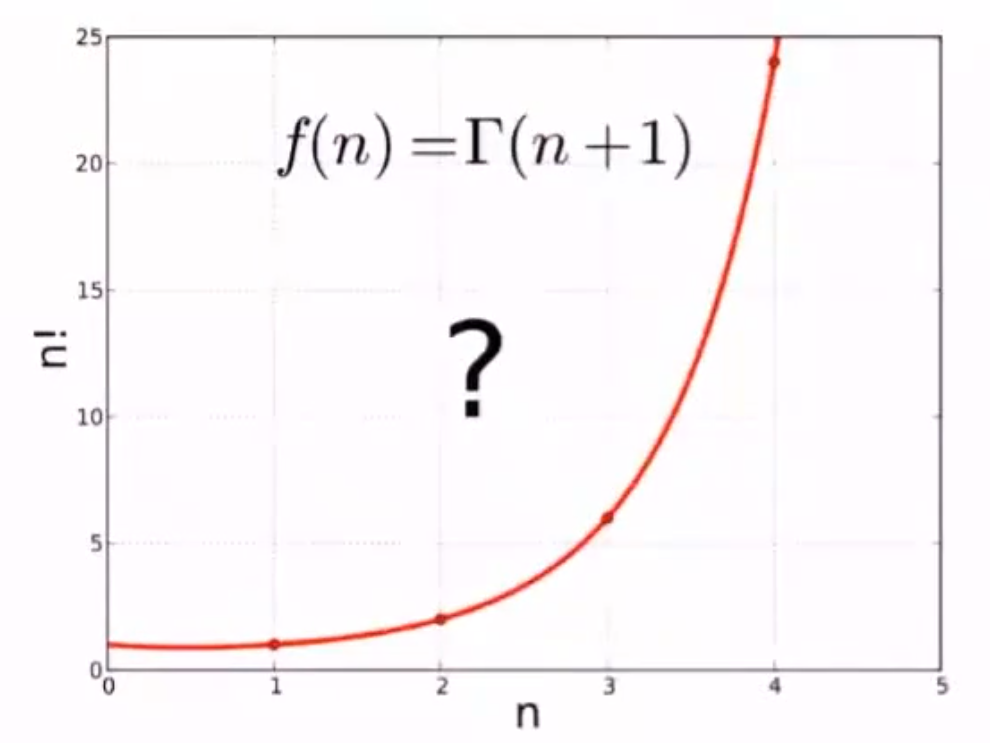
Γ ( z ) = ∫ 0 ∞ x z − 1 e − x d x \Gamma(z)=\int_{0}^{\infty}x^{z-1}e^{-x}dx Γ(z)=∫0∞xz−1e−xdx
Γ ( z + 1 ) = z ∫ 0 ∞ x z − 1 e − x d x = z Γ ( z ) \Gamma(z+1)=z\int_{0}^{\infty}x^{z-1}e^{-x}dx=z\Gamma(z) Γ(z+1)=z∫0∞xz−1e−xdx=zΓ(z)
Γ ( 1 ) = ∫ 0 ∞ x 1 − 1 e − x d x = 1 \Gamma(1)=\int_{0}^{\infty}x^{1-1}e^{-x}dx=1 Γ(1)=∫0∞x1−1e−xdx=1
Γ ( n ) = ( n − 1 ) ! \Gamma(n)=(n-1)! Γ(n)=(n−1)!
3.5.5 Beta分布
X ∼ B ( α , β ) X\sim B(\alpha,\beta) X∼B(α,β)
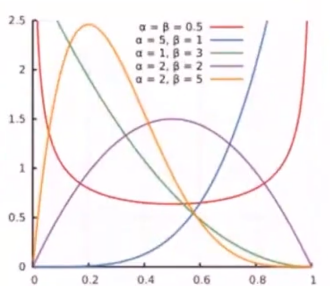
f ( x ; α , β ) = Γ ( α + β ) Γ ( α ) Γ ( β ) x α − 1 ( 1 − x ) β − 1 = x α − 1 ( 1 − x ) β − 1 B ( α , β ) f(x;\alpha,\beta)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)} f(x;α,β)=Γ(α)Γ(β)Γ(α+β)xα−1(1−x)β−1=B(α,β)xα−1(1−x)β−1

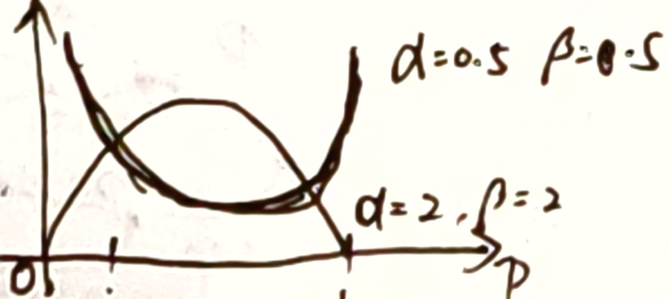
- α , β \alpha,\beta α,β 相等,则有对称性
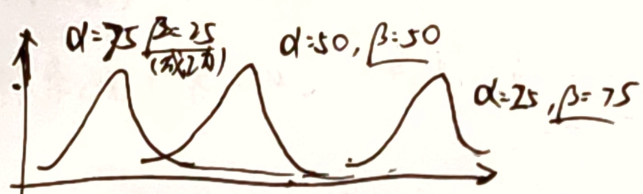
- 同样的历史数据,成功次数越少, P ( 成功 ) P(成功) P(成功) 越小
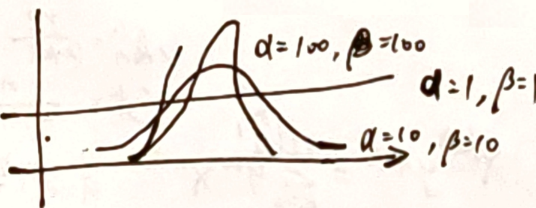
同一种情况的概率,历史数据越多,越确信
eg:
已知历史平均命中率0.266,编一组数据 B ( 81 , 219 ) B(81,219) B(81,219) 满足历史数据,通过现在的真实验数据修正模型
B e t a ( 81 , 219 ) → + 1 次 B e t a ( 82 , 219 ) → + 300 次 , 100 成功 , 200 失败 B e t a ( 81 + 100 , 219 + 200 ) Beta(81,219)\xrightarrow{+1次}Beta(82,219)\xrightarrow{+300次,100成功,200失败}Beta(81+100,219+200) Beta(81,219)+1次Beta(82,219)+300次,100成功,200失败Beta(81+100,219+200)
81 81 + 219 < 81 + 1 81 + 1 + 219 < 81 + 100 81 + 219 + 200 \frac{81}{81+219}<\frac{81+1}{81+1+219}<\frac{81+100}{81+219+200} 81+21981<81+1+21981+1<81+219+20081+100 可以看到成绩有所提升
3.5.6 正态分布
X ∼ N ( μ , σ 2 ) X\sim N(\mu,\sigma^2) X∼N(μ,σ2)
大部分随机变量呈现正态分布
- μ \mu μ 决定了平均水平
- σ \sigma σ 决定了平均水平附近的分散程度
f ( x ∣ μ , σ ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 f(x\vert \mu,\sigma)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x∣μ,σ)=2πσ1e−2σ2(x−μ)2
X ∼ N ( 0 , 1 ) X\sim N(0,1) X∼N(0,1) 为标准正态分布
3.5.7 泊松分布
X ∼ P ( μ ) = P ( λ t ) X\sim P(\mu)=P(\lambda t) X∼P(μ)=P(λt)
离散的正态分布,适用于随机实验中事件发生的次数(成功事件概率小)
假设:
- 任一事件的成功不影响另一事件成功(独立)
- 短片段成功概率与更长片段成功概率相等 ⇒ t ↑ \Rightarrow t\uparrow ⇒t↑ ,事件发生次数 ↑ \uparrow ↑
- 区间小时事件成功概率趋于0
P ( X ∣ λ ) = μ k k ! e − λ , k = 0 , 1 , ⋯ P(X\vert \lambda)=\frac{\mu ^k}{k!}e^{-\lambda},k=0,1,\cdots P(X∣λ)=k!μke−λ,k=0,1,⋯
- ( λ :单位时间内发生次数 ) (\lambda:单位时间内发生次数) (λ:单位时间内发生次数) μ = λ t \mu=\lambda t μ=λt
n n n 很大, p p p 很小的二项分布用泊松分布代替
eg:
平均每小时出生3婴儿,下一小时出生情况
P ( N ( t ) = n ) = ( λ t ) n n ! e − λ t P(N(t)=n)=\frac{(\lambda t)^n}{n!}e^{-\lambda t} P(N(t)=n)=n!(λt)ne−λt 表示t时间内事件发生n次的概率
2个小时内一个都不出生, P ( N ( 2 ) = 0 ) = e − 3 × 2 ≈ 0.0025 P(N(2)=0)=e^{-3\times 2}\approx 0.0025 P(N(2)=0)=e−3×2≈0.0025
1个小时至少2个, P ( N ( 1 ) ≥ 2 ) = 1 − P ( N ( 1 ) = 0 ) − P ( N ( 1 ) = 1 ) ≈ 0.8 P(N(1)\ge 2)=1-P(N(1)=0)-P(N(1)=1)\approx 0.8 P(N(1)≥2)=1−P(N(1)=0)−P(N(1)=1)≈0.8
E X = λ t EX=\lambda t EX=λt D X = λ t DX=\lambda t DX=λt
3.5.8 指数分布
X ∼ E X P ( λ ) X\sim EXP(\lambda) X∼EXP(λ)
泊松分布事件中,第 k k k 次随机时间与第 k + 1 k+1 k+1 次随机事件出现的时间间隔服从指数分布
- 事件以恒定的平均速率连续且独立地发生的过程
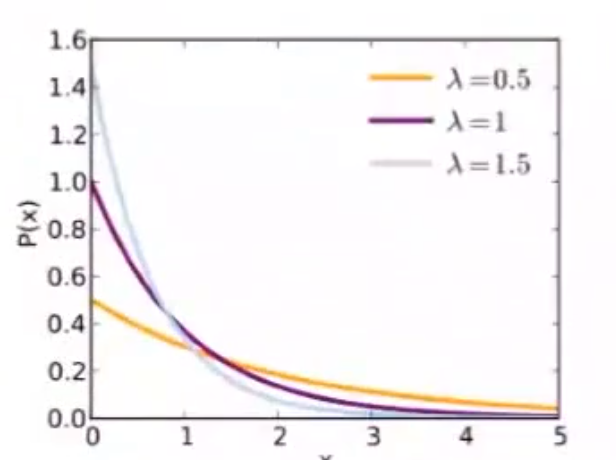
f ( x ; λ ) = { λ e − λ x , x ≥ 0 0 , x < 0 f(x;\lambda)=\begin{cases}\lambda e^{-\lambda x}&,x\ge 0\\0&,x<0\end{cases} f(x;λ)={λe−λx0,x≥0,x<0 , λ :单位时间发生该事件的次数 \lambda:单位时间发生该事件的次数 λ:单位时间发生该事件的次数
F ( x ; λ ) = { 1 − e − λ x , x ≥ 0 0 , x < 0 F(x;\lambda)=\begin{cases}1-e^{-\lambda x}&,x\ge 0\\0&,x<0\end{cases} F(x;λ)={1−e−λx0,x≥0,x<0
-
E X = 1 λ EX=\frac{1}{\lambda} EX=λ1
-
D X = 1 λ 2 DX=\frac{1}{\lambda^2} DX=λ21
每小时接2个电话,两个电话之间等待时间为半小时
无记忆性
P ( T > s + t ∣ T > t ) = P ( T > s ) P(T>s+t\vert T>t)=P(T>s) P(T>s+t∣T>t)=P(T>s)
3.5.9 卡方分布
适用:通过小数量样本估计总样本分布
卡方检验:检验样本值与理论值间的偏离程度
随机变量 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn 相互独立,且 X i ( i = 1 , 2 , ⋯ , n ) X_i(i=1,2,\cdots,n) Xi(i=1,2,⋯,n) 服从 N ( 0 , 1 ) N(0,1) N(0,1) ,则其平方和 ∑ i = 1 n X i 2 ∼ χ ( n ) \sum\limits_{i=1}^n X_i^2\sim \chi(n) i=1∑nXi2∼χ(n)
- E ( χ 2 ) = n E(\chi^2)=n E(χ2)=n
- D ( χ 2 ) = 2 n D(\chi^2)=2n D(χ2)=2n


























 50
50











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










