【矩阵论】2. 矩阵分解——正定阵分解

矩阵论的所有文章，主要内容参考北航赵迪老师的课件

[注]由于矩阵论对计算机比较重要，所以选修了这门课，但不是专业搞数学的，所以存在很多口语化描述，而且对很多东西理解不是很正确与透彻，欢迎大家指正。我可能间歇性忙，但有空一定会回复修改的。

矩阵论
1. 准备知识——复数域上矩阵,Hermite变换)
1.准备知识——复数域上的内积域正交阵
1.准备知识——Hermite阵，二次型，矩阵合同，正定阵，幂0阵，幂等阵，矩阵的秩
2. 矩阵分解——SVD准备知识——奇异值
2. 矩阵分解——SVD
2. 矩阵分解——QR分解
2. 矩阵分解——正定阵分解
2. 矩阵分解——单阵谱分解
2. 矩阵分解——正规分解——正规阵
2. 矩阵分解——正规谱分解
2. 矩阵分解——高低分解
3. 矩阵函数——常见解析函数
3. 矩阵函数——谱公式,幂0与泰勒计算矩阵函数
3. 矩阵函数——矩阵函数求导
4. 矩阵运算——观察法求矩阵特征值特征向量
4. 矩阵运算——张量积
4. 矩阵运算——矩阵拉直
4.矩阵运算——广义逆——加号逆定义性质与特殊矩阵的加号逆
4. 矩阵运算——广义逆——加号逆的计算
4. 矩阵运算——广义逆——加号逆应用
4. 矩阵运算——广义逆——减号逆
5. 线性空间与线性变换——线性空间
5. 线性空间与线性变换——生成子空间
5. 线性空间与线性变换——线性映射与自然基分解,线性变换
6. 正规方程与矩阵方程求解
7. 范数理论——基本概念——向量范数与矩阵范数
7.范数理论——基本概念——矩阵范数生成向量范数&谱范不等式
7. 矩阵理论——算子范数
7.范数理论——范数估计——许尔估计&谱估计
7. 范数理论——非负/正矩阵
8. 常用矩阵总结——秩1矩阵，优阵(单位正交阵)，Hermite阵
8. 常用矩阵总结——镜面阵，正定阵
8. 常用矩阵总结——单阵，正规阵，幂0阵，幂等阵，循环阵

---

矩阵分解可以得到简化的乘积矩阵，可以简化后续的计算与处理度

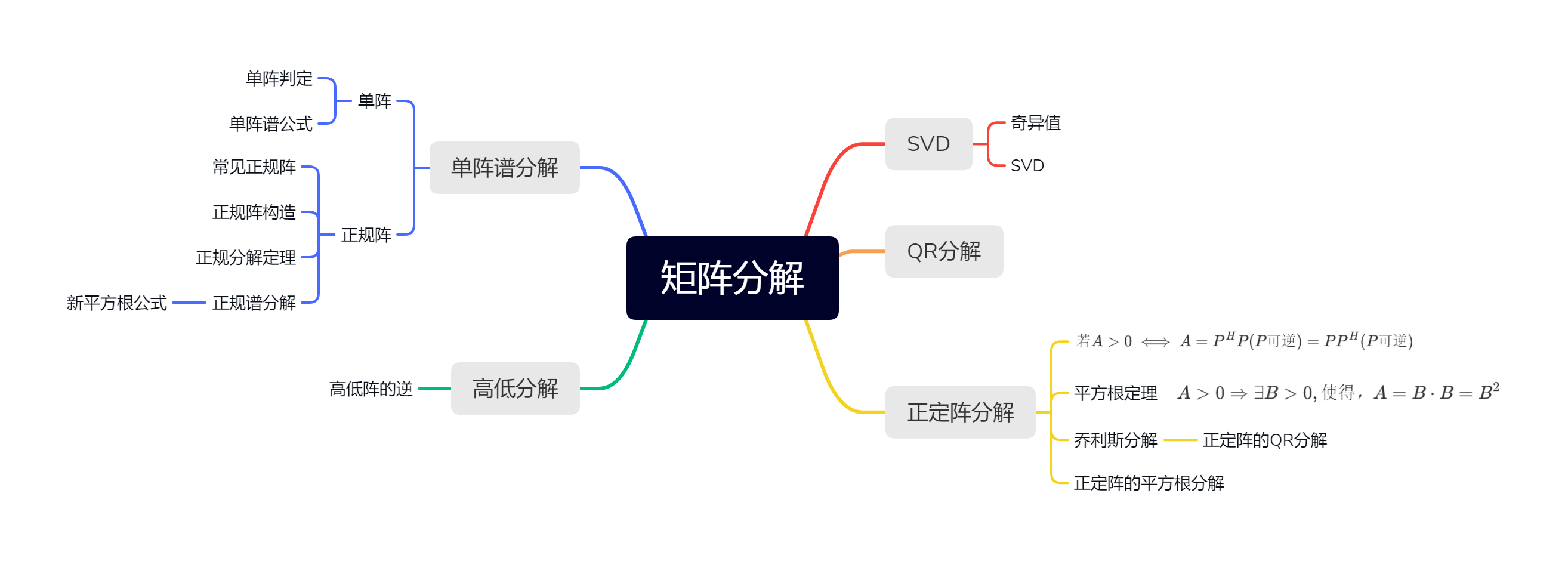
2.3 正定阵分解

a. $A=P^{H}P$

定理：$A>0⟺A=P^{H}P(P可逆)=P{P}^H(P可逆)$

$\Rightarrow$

若 $A$ 是正定阵，则 $A$ 必是Hermite阵，$A$ 的特征值是正实数。

又 $\because$ 正定阵一定与单位阵合同，即 $A\stackrel{\Delta }{=}\Lambda =\sqrt{\Lambda }I\sqrt{\Lambda }$ ,

令 $P=\sqrt{\Lambda }$ ，可知 $P$ 可逆，且 $P^H=P$

得证结论，$A>0\Rightarrow A=P^{H}P=P{P}^H$

$\Leftarrow$

• 若 $A=P^{H}P=P^{H}IP$ ，由于 $P$ 可逆，则 $A\stackrel{\Delta }{=}I>0$ ，则 $A$ 是正定阵
• 由二次型 $X^{H}AX=X^H{P}^{H}PX=(PX{)}^H(PX)=|PX{|}^2>0$ ，为正定二次型 $\therefore A$ 是正定阵

b. 平方根定理

$A>0\Rightarrow \exists B>0$ ，使得 $A=B\cdot B=B^2$

证明：

1. $\exists B,使得A=B\cdot B$
   $$\begin{array}{rl}& \because A>0，则A^H=A，\\ & 由Hermite分解定理\Rightarrow 存在U阵Q，使得Q^{H}AQ=\Lambda \\ & =\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_n\end{array}\right)={\left(\begin{array}{ccc}\sqrt{{\lambda }_1}& & \\ & \ddots & \\ & & \sqrt{{\lambda }_n}\end{array}\right)}^2={\Lambda }^{\prime 2},({\lambda }_i>0)\\ & 而A=Q\Lambda Q^H=Q\sqrt{\Lambda }\sqrt{\Lambda }{Q}^H=Q\sqrt{\Lambda }{Q}^{H}Q\sqrt{\Lambda }{Q}^H\\ & 令B=Q\sqrt{\Lambda }{Q}^H，则A=B^2\end{array}$$

2. $B是正定Hermite阵$

   由Hermite分解定理，$\exists$ U阵 $Q$ ，使得 $Q^{H}AQ=\Lambda ={\left(\begin{array}{ccc}\sqrt{{\lambda }_1}& & \\ & \ddots & \\ & & \sqrt{{\lambda }_n}\end{array}\right)}^2={\Lambda }^{\prime 2},{\Lambda }^{\prime }=\sqrt{\Lambda }>0$ ，为正定阵

   已知 $Q^H\sqrt{\Lambda }Q=B$ ，即 $B\stackrel{\Delta }{=}\sqrt{\Lambda }>0$ ，$B$ 为正定阵

平方根公式

$$\begin{array}{rl}& B=\sqrt{A}=Q\left(\begin{array}{ccc}\sqrt{{\lambda }_1}& & \\ & \ddots & \\ & & \sqrt{{\lambda }_n}\end{array}\right)Q^H\end{array}$$

c. 乔利斯分解——正定阵的QR分解

若 $A>0(正定)$ ，则有 $A=R^{H}R$ ，其中 $R=\left(\begin{array}{ccc}{b}_1& & \ast \\ & \ddots & \\ 0& & b_n\end{array}\right)$ 为上三角阵，且 $b_1>0,\cdots ,b_n>0$ ，则 $A=R^{H}R$ 为乔利斯分解

证明
$$\begin{array}{rl}& A>0必有可逆阵P，使A=P^{H}P,对P使用QR分解，其中R为上三角，Q为U阵\\ & \Rightarrow A=P^{H}P=(QR{)}^H(QR)=R^H(Q^{H}Q)R=R^{H}R\\ & 可写分解：A=R^{H}R,R=\left(\begin{array}{ccc}{b}_1& & \ast \\ & \ddots & \\ 0& & b_n\end{array}\right)为上三角，且b_1>0,\cdots ,b_n>0\end{array}$$

d. 平方根分解

$A>0(正定)$ ，则有 $A=B^2,B>0(正定)$ ，且矩阵 $B$ 唯一，可写 $B=\sqrt{A},A=(\sqrt{A}{)}^2$

证明
$$\begin{array}{rl}& 对A>0，必有Hermite分解(Q为U阵)：\\ & A=Q\Lambda Q^H,其中\Lambda =\left(\begin{array}{ccc}{\lambda }_1& & 0\\ & \ddots & \\ 0& & {\lambda }_n\end{array}\right),{\lambda }_i>0\\ & 令\sqrt{\Lambda }=\left(\begin{array}{ccc}\sqrt{{\lambda }_1}& & 0\\ & \ddots & \\ 0& & \sqrt{{\lambda }_n}\end{array}\right),且\sqrt{\Lambda }为正定阵\\ & 令B=Q\sqrt{\Lambda }{Q}^H\Rightarrow B为正定Hermite阵(\lambda (B)>0)\\ & B^2=(Q\sqrt{\Lambda }{Q}^H)(Q\sqrt{\Lambda }{Q}^H)=Q\Lambda Q^H=A\end{array}$$