（一）密码学之数论基础

1，数论基础

1.1，欧几里得算法：

如果a=bq+r, b≠0且a、b、q、r为整数，则 gcd(a, b)=gcd(b, r)；

其实这就是除法求余的过程：我们令a=b,b=a/b®;也叫辗转相除法啊。

于是，我们还有另外一种形式：gcd(a, b)=gcd(b, a (mod b))

//这里贴一下欧几里得算法
//递归形式的更加清晰
int ojld(int m,int n){
  if(m%n==0){
      return n;
  }
  return ojld(n,m%n);
}

1.2，扩展欧几里得算法

问题引入：

对于整数a和正整数b，当gcd(a, b)=1时存在整数c， 使得ac ≡ 1 (mod b)；称c为a关于模b的乘法逆元，记为$a^{-1}$。

对于给定的整数a和b，扩展的欧几里得算法不仅可以计算出最大公因子d，而且还有另外两个整数s和t，使得满足如下方程:

as+bt = d = gcd(a, b)。

另外，根据互素的性质，存在s和t，使得as+nt=1，而nt≡0 (mod n)，所以s是a关于模n的乘法逆元，即$a^{-1}=s$。由此，我们可以使用扩展欧几里得算法求解逆元了。注意，乘法逆元不唯一，但在mod n下是唯一的。

计算方法：采取添加单位矩阵的方式，进行列变换，直到某列出现1。此时我们将当前列中的绝对值大数乘以原式中的小数，类似即可得到我们想要的结果。

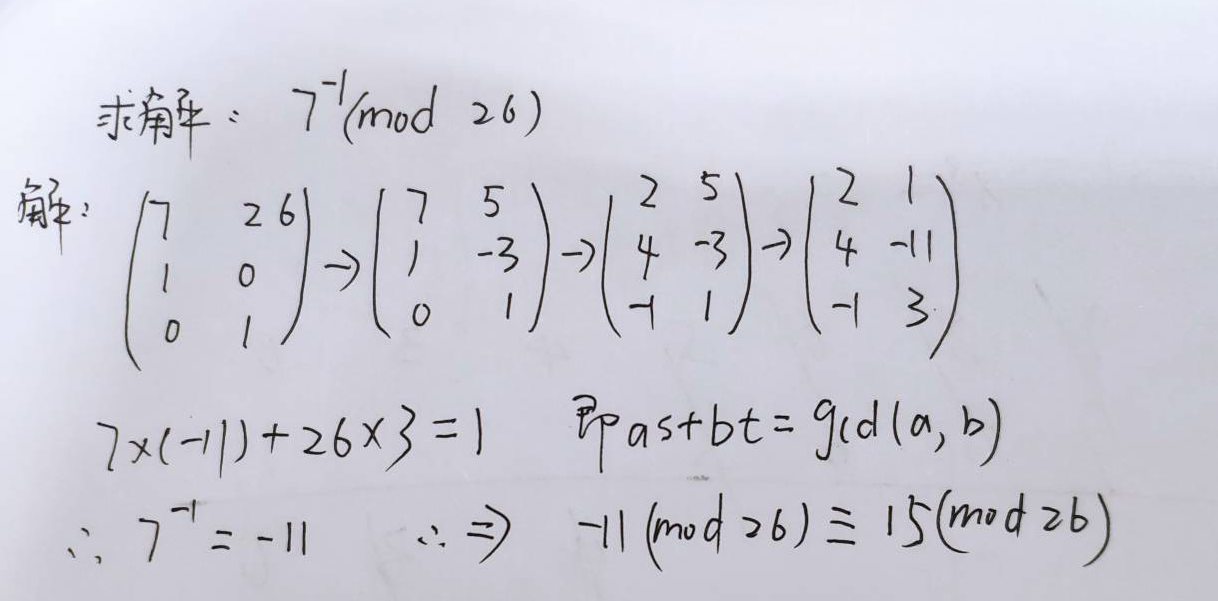
如果（a mod n) = (b mod n)，那么称a,b模n同余,记为 $a\equiv b\mathrm{m}\mathrm{o}\mathrm{d}n$；

费马定理：如果p是素数，并且a是不能被p整除的正整数，则$a^{p-1}\equiv 1(modp)$;

另一等价形式：如果p是素数，a是任意的正整数且gcd(a, p)=1，则有$a^p\equiv a(modp)$。

欧拉函数：欧拉函数φ(n)表示比n小且与n互素的正整数的个数。

欧拉函数具有如下性质：

1，当n是素数时，有φ(n)=n-1；因为素数与每一个小于他的数都是互素关系
2，当n=pq，且p和q是互异的素数时，则有φ(n)=φ(pq)=φ§×φ(q)=(p-1)×(q-1)；

证明：φ(pq)=φ( p)×φ(q)

参考中国剩余定理：

设a与p互素，b与q互素，c与pq互素；则c与（a，b）一一对应关系；

又由于a的值有φ§种可能，b的值有φ(q)种可能，c的值有φ(pq)种可能，而（a，b）有φ( p)φ(q)种可能；所以φ(pq)=φ( p)×φ(q)。

3，$\phi (p^k)=p^k-p^{k-1}=p^k(1-\frac{1}{p})$,因为$p^k$个数减去所有p的倍数即为p的质数；

欧拉定理：

任意互素的两个整数a（a≠0）和n（n>1），且gcd(a, n)=1，则：

$a^{\phi (n)}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}n)$或$a^{\phi (n)+1}\equiv a(\mathrm{m}\mathrm{o}\mathrm{d}n)$

如果n为素数p，则φ(n)=φ§=p-1，即为费马定理$a^{p-1}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}p)$。

离散对数：