（一）图——图论笔记系列

1，图论

1,1，图的基本概念

define1：无向图，是由一个有序二元组G<V,E>;V表示顶点集，E表示边集，E中的元素为无向边。

define2：有向图，即无向图中所有的边均为有向边。

其中，相邻的称为邻接；两点确定的边称为他们是关联的。

无边关联的点称为孤立点，一条边关联的两个结点重合，称为环或自回路。

注意：我们讨论的通常是有限图，其中|V|=n,|E|=0的图称为n阶零图；只有一个顶点的图称为平凡图。

关联于同一结点的两条边称为平行边；不含平行边和环的图称为简单图，我们也主要讨论简单图。

define3：与v相关联的边的次数称为v的度数，有入度和出度之分,分别记为$deg(v{)}^{-},deg(v{)}^{+}$。

握手定理：一个图的度数是边的两倍。

推论：任一图中，奇度结点必有偶数个，结点的度数最多位n-1；

有向图中，入度=出度=边数。

1.2，图的基本分类

define4：无向简单图G，任意两个结点之间都有边相连，我们称之为完全图。n个结点的完全图记为$K_n$

相应的，有向简单图中，任意两结点之间都有一对方向相反的边相连，称之为有向完全图，记为$D_n$

其中，无向完全图的边数为$C_n^2=\frac{n(n-1)}{2}$,有向图变数为$n(n-1)$

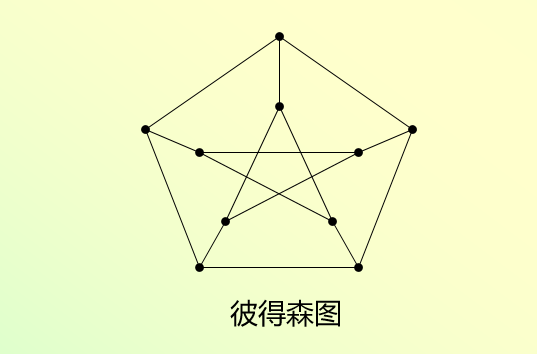
define5：如果一个无向简单图中，每个结点的度数均为K，称该图为k-正则图。完全图$K_n$是$n(n-1)$正则图.典型的3-正则图为彼得森图：

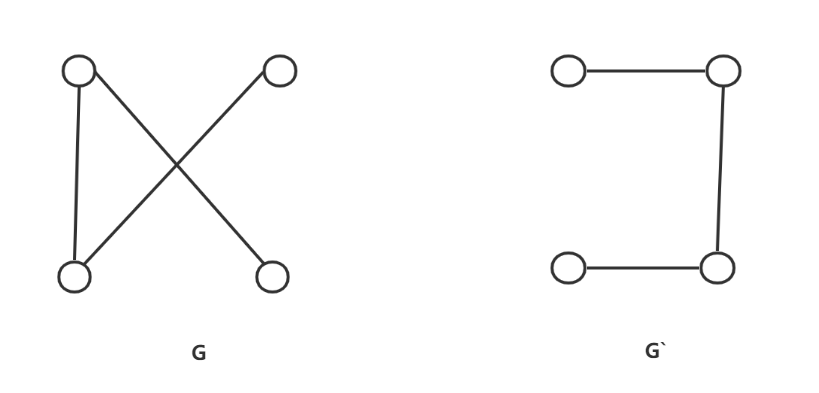
define6：给定图G,以G中所有结点为结点集，能够使G成为完全图所添加的边，构成的图称为G的补图，记为$\bar{G}$。可以看到G和G`合并后就是一个完全图了。

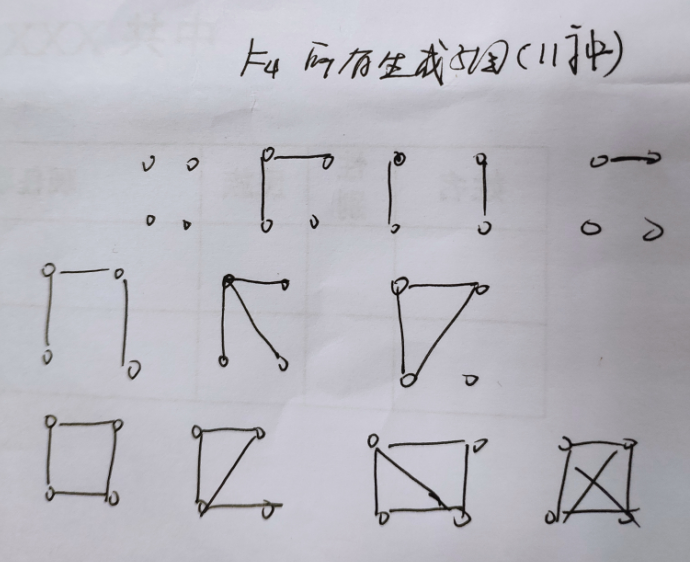
define7:子图与生成子图。生成子图比较重要，对于生成子图的构造，必须顶点个数一样，然后按照边数的多数进行推演。下面是K4的所有生成子图：

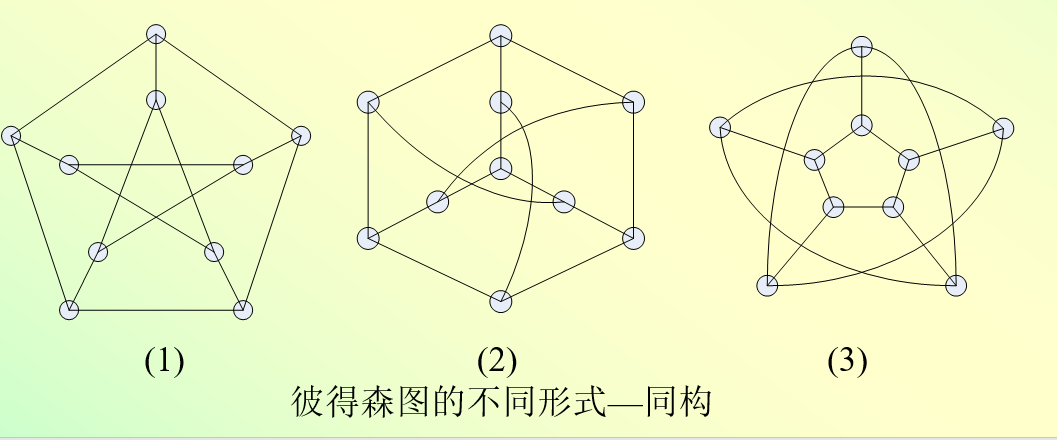
1.3，图的同构

图论中，我们只关心结点之间是否有连线，而不在意结点的位置和连线的形状，因此，同一图的图形表示不唯一。

同构的必要条件：

1）结点数相等；2）边数相等；3）度数相同的结点数目相同，即度数序列相同。

两个图同构的判断非常困难，需要仔细考察图的结点和边的关联关系。

1.4，图的连通性

define1：无向图中任意两个结点都是连通的，则称图是连通图。

define2：D是有向图，若去掉各边的方向后是连通图，则称D是弱联通图；

相应的，D中任意两结点都可达，D是强连通图；

若D中任意两点至少一个可达另一个，则图D是单向连通图。

define3：一条回路的起点和内部结点互不相同，称为圈。

割点：删掉一个点后，子图不再连通。点割集：割点组成的集合，但不允许有多余的点。

注意：割点只能是一个点，而点割集可以是一个点，也可以是多个点的集合。

割边（桥）：删掉一条边后，子图不再连通。边割集：割边组成的集合，但不允许有多余的边。

点连通度（连通度）：最小的构成连通的点的个数。

点连通度：设G是无向连通图，如果G不是完全图，k(G)=min{|V1||V2}是G的点割集，称为图G的点连通度；

物理意义：要使G成为不连通的最少要删除的结点数。如果一个图的点连通度是1，最少删除一个结点，图变为不连通的

同理，边连通度类似。

二部图：若能将V分成V1和V2，使得G中的每条边的两个端点都是一个属于V1，一个属于V2,那么称为二部图。

二部图的判定：一个无向图是二部图当且仅当G中无奇数长度的回路。

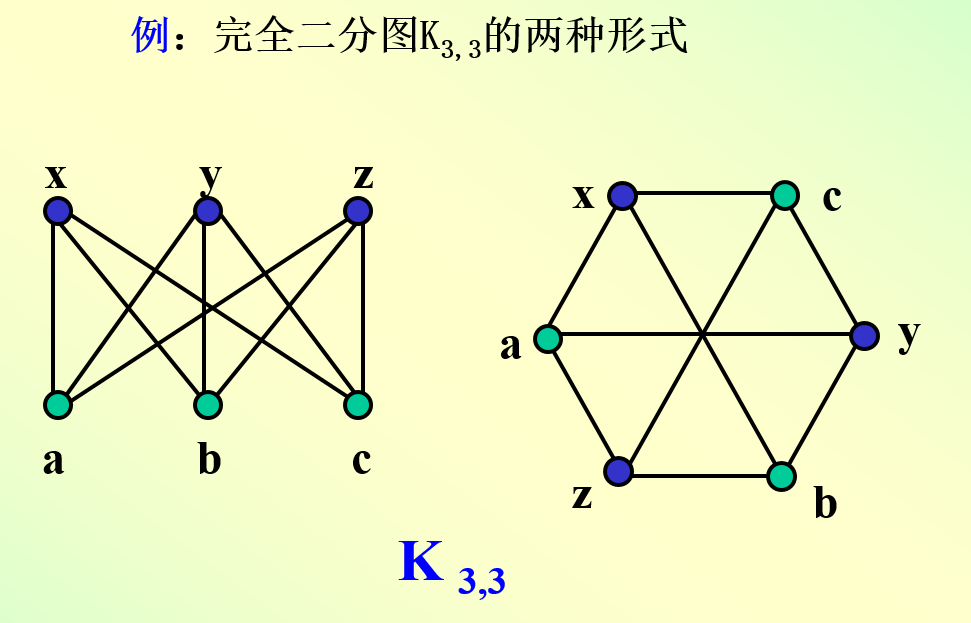
1.5，图的矩阵表示

1.5.1，无向图的关联矩阵：

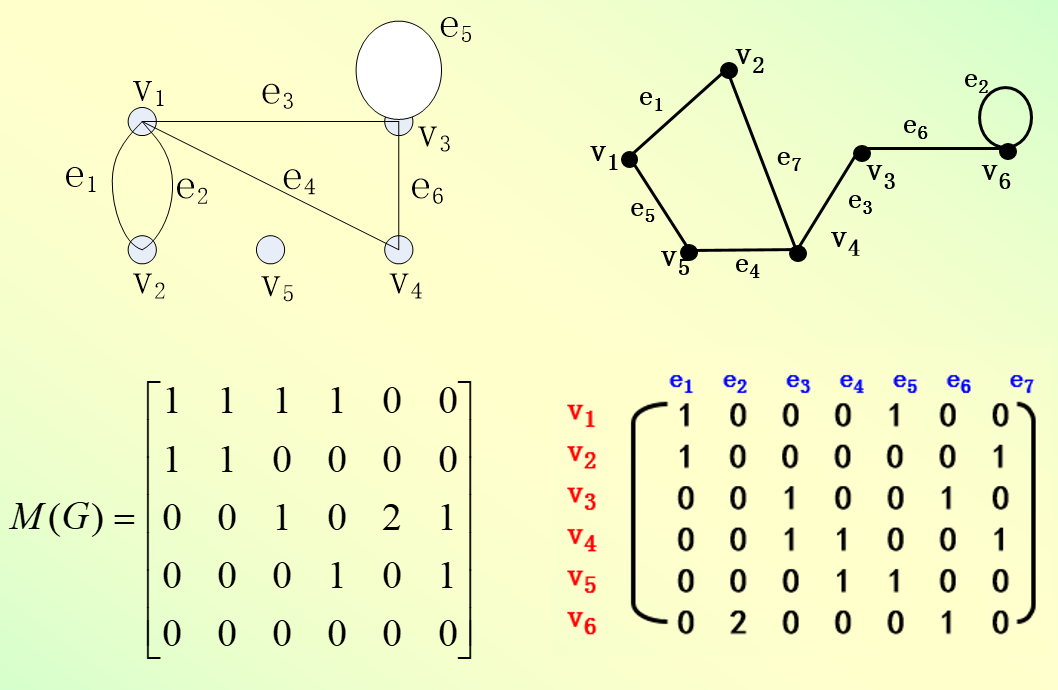
无向图关联矩阵的性质：

设G=<V,E>是无向图，G的关联矩阵M(G)有以下的性质：
①每列元素之和均为2。这说明每条边关联两个结点。
②每行元素之和是对应结点的度数。
③所有元素之和是图各结点度数的和，也是边数的2倍。
④两列相同，则对应的两个边是平行边。
⑤某行元素全为零，则对应结点为孤立点。

1.5.2，无环有向图的关联矩阵

无环有向图关联矩阵的性质：

设G=<V,E>是无环有向图，G的完全关联矩阵M(G)有以下的性质：
①每列有一个1和一个-1，这说明每条有向边有一个始点和一个终点。
②每行1的个数是对应结点的出度，-1的个数是对应结点的入度。
③所有元素之和是0，这说明所有结点出度的和等于所有结点入度的和。
④两列相同，则对应的两边是平行边。

1.5.3，有向图的邻接矩阵

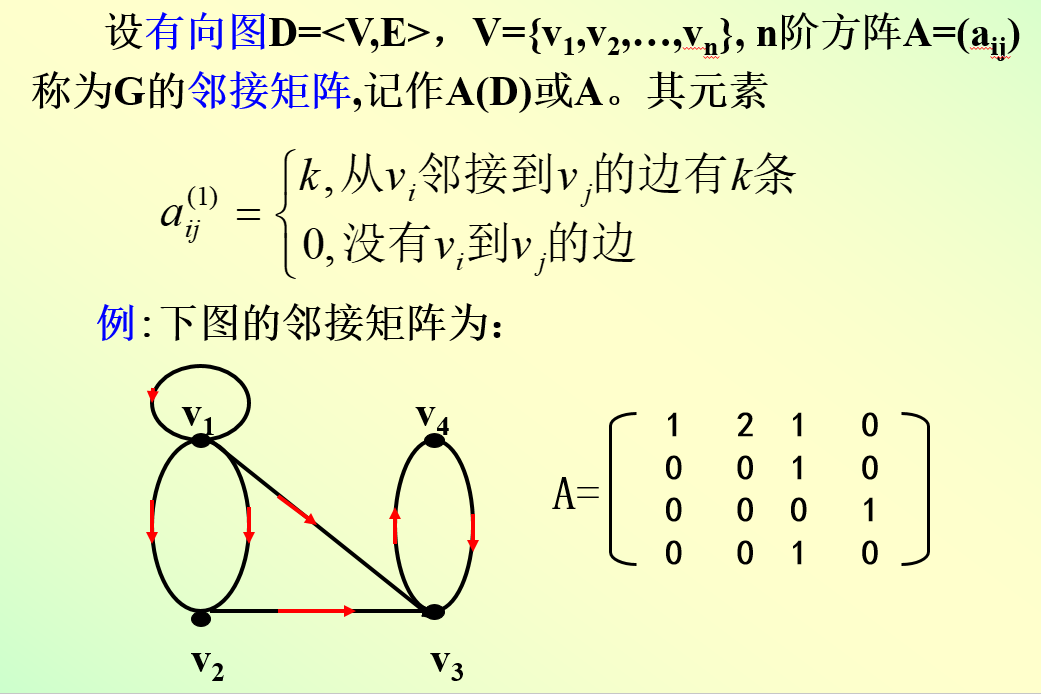
我们来考察$A^l$的元素的意义：$a_{ij}$表示vi到vj路径为l的通路的数目.

1.5.4，无向图的邻接矩阵

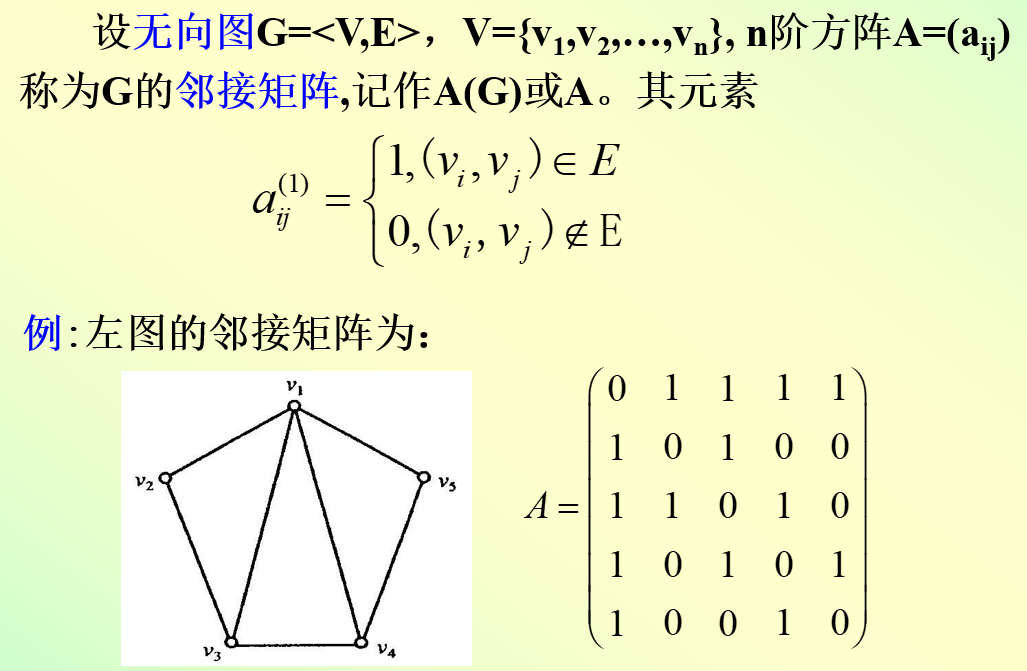
1.5.5，有向图的可达矩阵

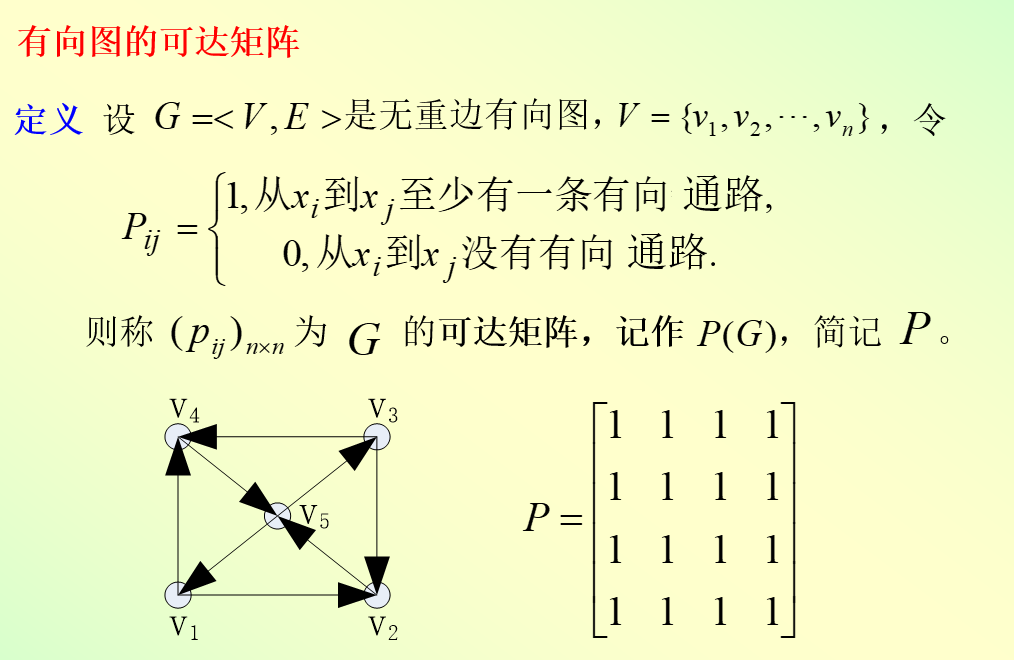
可由邻接矩阵得到可达矩阵：即令R=$A+A^2+...+A^n$,再将其中的非零元素置为1即可。

另外$A,A^2,A^3,A^4$分别是长度为1，2，3，4的通路所对应的描述，则vi到vj对应的通路长度即为aij。

tips:关联矩阵描述的是边和点的关系；而邻接矩阵描述的是点和点关系。

1.6，欧拉图与哈密顿图

欧拉通路：通过图(无向图或有向图)中所有边一次且仅一次行遍所有顶点的通路；

欧拉回路：通过图(无向图或有向图)中所有边一次且仅一次行遍所有顶点的回路；

欧拉图：具有欧拉回路的图。规定：平凡图是欧拉图；

半欧拉图：具有欧拉路而无欧拉回路的图。

欧拉图的判定：当且仅当图G中无奇度结点。

定理：无向图G具有一条欧拉路，当且仅当G是连通的且有零个或两个奇度结点。

哈密顿通路：经过图（有向图或无向图）中所有顶点一次且仅一次的通路；

哈密顿回路：经过图中所有顶点一次且仅一次的回路；

哈密顿图：具有哈密顿回路的图。规定：平凡图是哈密顿图；

半哈密顿图：具有哈密顿通路但不具有哈密顿回路的图。