3D数学基础学习笔记

左手坐标系：横向为X轴，正方向为右。纵向为Y轴，正方向为上。Z轴正方向为屏幕外指向屏幕内。
右手坐标系：横向为X轴，正方向为右。纵向为Y轴，正方向为上。Z轴正方向为屏幕内指向屏幕外。
常用的几个坐标系：
3D笛卡尔坐标系：右手坐标系。
OpenGl：右手坐标系。
Direct3D：左手坐标系。
Unity3D：左手坐标系。

Unity中的使用的几种坐标系：
1、全局坐标系。
2、局部坐标系（本地坐标系，以父物体的position为原地做基准）。
3、屏幕坐标系（分辨率坐标系）：左下角为（0,0），右上角为Screen.Width，Screen.Height，Z轴的坐标是相机的世界坐标中Z轴坐标的负值。可以通过Input.mousePosition获取鼠标的坐标。
4、视口坐标系。左下角0，0.右上角1,1。 是将Game视图的屏幕坐标系单位化。

全局坐标系和局部坐标系之间的转换：
Transform.TransformPoint(Vector3 position) :将一个坐标点从局部坐标系转换到全局坐标系。
Transform.InverseTransformPoint(Vector3 position)：将坐标点从全局坐标系转换到局部坐标系
Transform.TransformDirection(Vector3 direction):将一个方向从局部坐标系转换到全局坐标系。
Transform.InverseTransformDirection(Vector3 direction)：将一个方向从全局坐标系转换到局部坐标系。
Transform.TransformVector(Vector3 vector):将一个向量从局部坐标系转换到全局坐标系。
Transform.InverseTransformVector(Vector3 vector):将一个向量从全局坐标系转换到局部坐标系。
PS：
Transform.forward, Transform.right, Transform.up：当前物体的物体坐标系的z轴，x轴，y轴在世界坐标系上的指向。

屏幕坐标系与全局坐标系之间的转换：
Camera.ScreenToWorldPoint(Vector3 position): 将屏幕坐标转换为全局坐标。
Camera.WorldToScreenPoint(Vector3 position):将全局坐标转换为屏幕坐标。

屏幕坐标系与视口坐标系之间的转换：
Camera.ScreenToViewportPoint(Vector3 position)：将屏幕坐标转换为视口坐标。
Camera.ViewportToScreenPoint(Vector3 position)：将视口坐标转换为屏幕坐标。

全局坐标系与视口坐标系之间的转换：
Camera.WorldToViewportPoint(Vector3 position)：将全局坐标转换为视口坐标。
Camera.ViewportToWorldPoint(Vector3 position)：将视口坐标转换为全局坐标。

向量：
1、向量的定义：
在数学中，向量也称为矢量，是指具有大小和方向的量。
向量的大小就是向量的长度，也叫做模。向量的仿效描述了空间中向量的指向。
2、点和向量的关系：
点：只是表示一个位置，它没有大小与方向。2D用（x，y）表示，3D用（x，y，z）表示。
向量：表示了向量在每个维度上的有向位移。
3、unity中的点和向量：
Vector2类型可以用来表示2D的向量和点。Vector3类型可以用来表示3D的向量和点。

向量运算：
1、零向量
零向量是一个特殊的向量，没有大小没有方向。
2、负向量
一个向量和它的负向量相加等于0向量。大小相等，方向相反。
3、向量的长度
向量的长度即向量的大小或者向量的模。
向量的大小就是各维度的平方和的平方根。
在unity中，可以通过Vector3.Magnitude计算向量的长度。
Vector3.SqrMagnitude获取向量长度的平方。
4、向量与标量的乘/除
标量分别于向量的各维度实现乘/除。
在unity中使用*与/符号。
5、单位向量
单位向量也叫做标准化向量，就是大小为1的向量。
在只关心向量方向，不关心向量大小时，可以使用单位向量，例如求一个面的发现向量时。
对于任意的非零向量，可以使用归一化（Vector3.Normalize）获取它的单位向量。
6、向量的加法与减法
只有维度相同的向量可以加减，例如2D与2D，3D与3D，2D与3D不行。
向量的加减就是各维度的加减。
向量满足加法交换律，不满足减法交换律。
7、向量的点积
向量与向量的乘法有两种不同的形式，第一种是向量的点积，也叫做向量的内积。
表示为a·b，符号“·”不可省略。
计算结果是各维度相乘然后相加，得到的结果是一个标量。
公式：a·b= axbx+ayby
满足交换律。
点积的第二种计算方式是通过两个向量之间的夹角cos值
公式：a·b = | a || b | cosθ，θ是向量a与向量b的夹角。
点乘的结果越大，两向量越接近。通常也被用来求两个向量之间的夹角的大小。
可以通过向量的点积的结果的符号来判断两个位置向量的关系。
如果值大于0，则夹角在0度到90度之间(不包含90度)，两个向量的方向基本相同。
如果值等于0，则夹角为90度，两个向量的方向相互垂直。
如果值小于0，则夹角在90度到180度之间(不包含90度)，两个向量的方向基本相反。
向量的点积还可以用来求得一个向量在另一个向量上的投影。

在Unity中，向量的点积可以通过Vector3.Dot来计算。
可以使用Vector3.Angle来获得两个向量之间夹角的大小。结果在0~180度之间。
8、向量的叉积
两个向量相乘的第二种方式成为向量的叉积，也叫做向量的外积。
表示为 aXb 同样，X也不可省略。
叉积的结果仍然为一个向量。
叉积仅可应用于3D向量。
叉积的计算公式为
a×b = (ax, ay, az)×(bx, by, bz) = (aybz - azby, azbx - axbz, axby - aybx)
叉积得到的向量垂直于原来的两个向量。
a×b的长度等于向量的大小与向量夹角的sin值的积，即
也是以a和b两边为平行四边形面积的大小。

可以通过向量的叉积来得到一个平面的法向量。
还可以通过向量的叉积得到的结果向量的方向来判断向量b是在向量a的顺时针方向还是逆时针方向。
在Unity中，向量的叉积可以通过Vector3.Cross来计算。

矩阵
1、矩阵的定义：
在数学中，矩阵是一个按照长方阵排列的复数或实数的集合。
向量的维度是看向量有几个分量。矩阵的维度则是看它有几行、几列。一个r×c矩阵有r行，c列。即2×3矩阵有2行3列。3×2矩阵则有3行2列。

在一个m×n的矩阵A中，有m×n个数，这些书称为矩阵A的元素。数aij位于矩阵的第i行，第j列，称为矩阵A的(i, j)元。
矩阵中元素的下标是从1开始，计算机中还是0开始。
在Unity中，可以使用Matrix4x4.SetRow和Matrix4x4.SetColumn来设置一个4×4矩阵的某行或某列。
在Unity中，可以使用Matrix4x4.GetRow和Matrix4x4.GetColumn来获取一个4×4矩阵的某行或某列。结果为Vector4类型。
2、矩阵和矩阵的加法/减法
只有维度相同的矩阵，才可以相加相减。
矩阵和矩阵的相加 / 相减即矩阵各相同位置的元素的相加相减。
3、矩阵和标量的乘法
矩阵和标量相乘，得到的仍然是一个相同维度的矩阵。矩阵和标量的乘法，即矩阵的每个元素和该标量相乘。

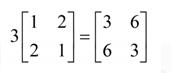
4、矩阵与向量的乘法
向量可以被当做一行或者一列的矩阵。3维向量可以看作是3×1矩阵，或是1×3矩阵。
矩阵和矩阵相乘时，只有满足第一个矩阵的列数和第二个矩阵的行数相等的条件时，才可以相乘。即r×n矩阵，才能和n×c矩阵相乘，得到的结果是一个r×c矩阵。
所以，向量与矩阵相乘时，行向量需要在左边，列向量需要在右边。
矩阵和向量相乘的结果向量中，每个元素都是原向量和矩阵中单独行或者列的点积。
5、矩阵和矩阵的乘法
两个矩阵相乘的规则和矩阵和向量相乘的规则相同。
矩阵A和矩阵B相乘，得到的矩阵C中的任意元素Cij等于A的第i行向量与B的第j列向量的点乘结果。
在Unity中，可以使用Matrix4x4.operator *来进行矩阵和矩阵的乘法运算。

6、特殊矩阵
1）方块矩阵
行数和列数相等的矩阵被称为方块矩阵。
方块矩阵中，行号和列号相等的元素叫对角元素。
如果一个矩阵除了对角元素外的所有元素都为0，那么这个矩阵就叫做对角矩阵。
如果对角矩阵中的对角元素都为1，则这个对角矩阵被称为单位矩阵。

用任意一个矩阵乘以单位矩阵，都将得到原矩阵。
在Unity中，可以通过Matrix4x4.identity来获得一个4×4的单位矩阵。
在Unity中，可以通过Matrix4x4.isIdentity来判断一个矩阵是不是单位矩阵。
在Unity中，可以通过Matrix4x4.zero获得一个4×4的所有元素都为0的矩阵。

2）转置矩阵
转置矩阵是对原矩阵进行转置运算后得到的矩阵。
一个r×c的矩阵转置后，可以得到一个c×r的矩阵。转置运算，即将原矩阵的第i行变为第i列，第j列变成第j行，也可以看作是沿着对角线翻折。
在Unity中，可以通过Matrix4x4.transpose获取一个矩阵的转置矩阵。

3）逆矩阵
只有方块矩阵才可能有逆矩阵，因为一个矩阵A和它的逆矩阵B需要满足条件：AB = I(I是单位矩阵)。
如果一个矩阵有相应的逆矩阵，则可以说这个矩阵是可逆的，或者说是非奇异的。如果一个矩阵没有相应的逆矩阵，则可以说这个矩阵是不可逆的，或者说是奇异的。
判断一个矩阵是否是可逆的，需要求得矩阵的行列式，如果它的行列式不为0，那么它就是可逆的。
二阶行列式的计算方法为对角线相乘相减。

三阶行列式的计算方法可以使用代数余子法，即行列式可以按某一行或某一列展开成元素与其对应的代数余子式的乘积之和。
行列式某元素的余子式：行列式划去该元素所在的行与列的各元素,剩下的元素按原样排列,得到的新行列式.
行列式某元素的代数余子式：行列式某元素的余子式与该元素对应的正负符号的乘积.

在Unity中，可以通过Matrix4x4.inverse来获取一个4×4矩阵的逆矩阵。

变换
1、齐次坐标
齐次坐标就是将一个原本是n维的向量用一个n + 1维向量来表示，是指一个用于投影几何里的坐标系统，如同用于欧氏几何里的笛卡儿坐标一般。
齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射几何变换。
(x, y, z)(x, y, z, 1)
一个标准的空间直角坐标系的基向量是a = (1, 0, 0),b = (0, 1, 0),c = (0, 0, 1)。原点为O。
我们可以使用基向量a,b,c来表示坐标系中任意一个向量v(vx, vy, vz)的坐标：v = vxa + vyb + vzc。
用基向量来表示坐标系中的任意一个点的位置，则需要考虑原点的位置，所以一个点P(px, py, pz)的坐标可以表示为：P = pxa + pyb + pzc + O。
用矩阵的形式来表示的话，可以表示为：

3D坐标系可以表示为：

点的齐次坐标表示：(x, y, z, 1)
向量的齐次坐标表示：(x, y, z, 0)
所以，我们可以用齐次坐标去进行点和向量之间的运算：
点与点之间的减法，可以的到一个向量。
向量和向量之间的加减，还是得到一个向量。
点和向量之间的加法，可以得到一个移动了向量距离之后的点。

仿射变换：
仿射变换 = 线性变换 + 平移。
线性变换：从代数上，是指可以保留矢量加和标量乘的变换。需要满足下面的2个条件。
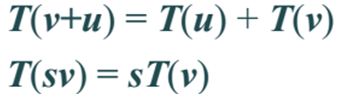从几何的角度上去理解，需要满足：
(1)变换前是直线的，变换后依然是直线。
(2)直线比例保持不变。
(3)变换前是原点的，变换后依然是原点。
旋转和缩放属于线性变换，但是平移不属于线性变换。
仿射变换，从几何的角度去理解，需要满足：
(1)变换前是直线的，变换后依然是直线。
(2)直线比例保持不变。
所以，平移、旋转、缩放都属于仿射变换。
仿射变换可以用矩阵和向量相乘的方式来表示。计算一个点或者一个向量，经过平移、旋转、缩放等仿射变换后的值。
一个三维的变换可以表示为：

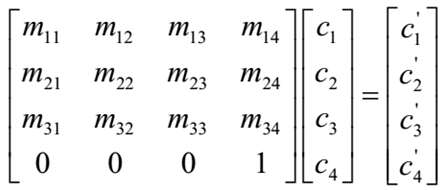
2D变换
2D平移矩阵：
2D缩放矩阵：
2D旋转矩阵：
变换矩阵的逆矩阵
平移矩阵的逆矩阵：
缩放矩阵的逆矩阵：
旋转矩阵的逆矩阵：

复合变换：
复合变换：我们可以把平移、旋转、缩放结合起来，形成一个复杂的变换过程。
矩阵乘法不满足交换律，所以不同的变换顺序得到的结果可能是不一样的。

3D矩阵：
3D平移矩阵：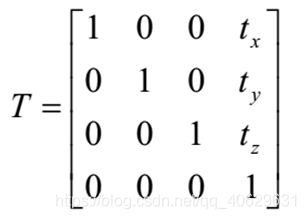
3D缩放矩阵：
3D旋转矩阵：

unity中的变换：
在Unity中，我们可以使用Matrix4x4.Translate创建一个平移矩阵。
在Unity中，我们可以使用Matrix4x4.Rotate创建一个旋转矩阵。
在Unity中，我们可以使用Matrix4x4.Scale创建一个缩放矩阵。
在Unity中，我们可以使用Matrix4x4.TRS创建一个移动、旋转、缩放的复合矩阵。
在Unity中，我们可以使用Matrix4x4.MultiplyPoint或者Matrix4x4.MultiplyPoint3x4来变换一个点。
在Unity中，我们可以使用Matrix4x4.MultiplyVector来变换一个向量。

总结完成：以上内容是根据SIKI学院学习所得。矩阵和变换总结的很糙，因为在实际工作中没有用到，并且API封装的很好，只是简单的学习了一下就过去了，因为本人从小到大很讨厌去学习log等函数，我个人更倾向于了解它有什么作用，如何去用，而不是钻研古人是怎么研究出来的，所幸unity中相关的API封装的很好，不需要自己去记一堆乱七八糟的公式。