GCN学习笔记

图卷积网络(Graph Neural Networks)

文是笔者对图卷积网络的一个学习，主要参考了网上的一些资料与李宏毅老师的视频。本文仅代表了笔者对于GCN的浅薄认识，如有错误，欢迎指出，共同进步。

1. 引言(Introduction)

图神经网络(Graph Neural Network)作为这几年新兴的神经网络，具有非常大的研究意义。因为图可以表示现实中各种非欧式空间的数据，包括城市交通网络，社交关系网络等。虽然传统的CNN在提取欧式空间的数据特征中取得了很大的成功，例如图像领域，但是这很难应用于非欧式空间中。因为图像是一个二维矩阵，而图是不规则的，图中的节点数量与连接方式都是不确定的。这导致了在图像上的一些重要运算在图中是无法计算的，如卷积。GCN作为GNN的第一种模型，可以说是GNN的开山之作，具有非常大的研究意义。

本文先介绍图的基础知识，然后主要介绍基于谱方法与空间域的GCN。

2. 图的基础知识(Basic Theory)

图(Graph)是数据结构与算法中一种强大的框架，并且图可以用来表示很多类型的系统，包括城市交通网络，社会关系等。图是由若干个节点以及连接两个节点之间的边组成。用数学公式表示一张图为：$G=(V,E)$，其中 V = { v 1 , v 2 , . . . } {V = \lbrace v_1, v_2, ... \rbrace} V={v1​,v2​,...}，表示节点组成的集合； E = { e 1 , e 2 , . . . } {E = \lbrace e_1, e_2, ... \rbrace} E={e1​,e2​,...}表示连接两个节点之间的边组成的集合。

图的分类有很多种，这里只讲有向图与无向图：

• 有向图(Directed Graph)：图的每一条边都带有方向；
• 无向图(Undirected Graph)：图的每一条边都没有方向。

本文中的讲解的GCN对象为无向图。还有一些需要用到的图论知识为：

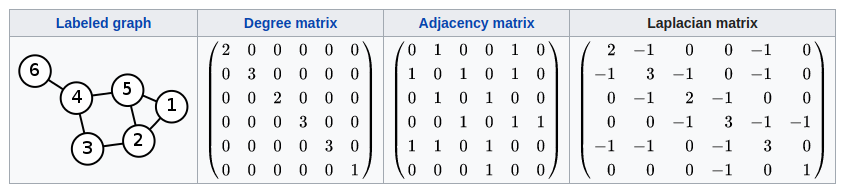
• 邻接矩阵A(Adjacency Matrix)：表示节点之间的相邻关系。在无向图中，$Aij=1$表示节点$i$与节点$j$相邻，并且为实对称矩阵；在有向图中$Aij=1$表示存在从节点$i$到节点$j$的边；
• 度矩阵D(Degree Matrix)：度矩阵是一个对角矩阵，其与邻接矩阵的关系为：$D_{ii}={\sum }_j{A}_{ij}$。并且$D_{ii}$表示与节点$i$相邻的边数；
• 拉普拉斯矩阵L(Laplacian Matrix)：也被称为导纳矩阵、基尔霍夫矩阵或离散拉普拉斯算子，其数学表达式为$L=D-A$。

拉普拉斯矩阵的变体有：

• 对称归一化拉普拉斯矩阵(Symmetric normalized Laplacian)
  $$L^{sys}=D^{-\frac{1}{2}}L{D}^{\frac{1}{2}}=I-D^{-\frac{1}{2}}A{D}^{\frac{1}{2}}\text{\hspace{1em}(1)}$$
  该矩阵元素定义为：
  $$L_{i,j}^{sys}=\{\begin{array}{ll}1& \text{i=j and diag(vi)=0}\\ -\frac{1}{\sqrt{diag(v_i)diag(v_j)}}& \text{i=j and vi is adjacent to vj}\\ 0& \text{otherwise}\end{array}$$

• 随机归一化拉普拉斯矩阵(Random Walk Normalized Laplacian)
  $$L^{rw}=D^{-1}L=I-D^{-1}A\text{\hspace{1em}(2)}$$
  该矩阵元素定义为：
  $$L_{i,j}^{rw}=\{\begin{array}{ll}1& \text{i=j and diag(vi)=0}\\ -\frac{1}{\sqrt{diag(v_i)}}& \text{i=j and vi is adjacent to vj}\\ 0& \text{otherwise}\end{array}$$

拉普拉斯矩阵具有非常优良的性质，包括：

• 半正定对称矩阵；
• 有n个线性无关的特征向量，并且其特征值非负，n为图中节点的数量；
• 由特征向量构成的矩阵为正交阵$U^{T}U=E$。

3. 频域图卷积(Spectral Convolution)

GCN对图进行卷积的主要思想是把图转换到频域(Frequency Domain)进行乘积运算后再转换回空间域(Spatial Domain)。所以核心问题在于如何把图转换到频域，再从频域转换回空间域。

3.1 拉普拉斯矩阵分解(Laplacian Matrix Decomposition)

转换的重点在与拉普拉斯矩阵的谱分解(Spectral Decomposition)。其实谱分解又被称为特征分解(Eigen Decomposition)，所以需要将矩阵映射到拉普拉斯矩阵的特征向量空间上。选择拉普拉斯矩阵是因为拉普拉斯是存在n个线性无关的特征向量的n阶方阵。拉普拉斯矩阵的谱分解可以写成：
$$L=U\Lambda U^{-1}=U\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right]U^{-1}\text{\hspace{1em}(3)}$$
其中$U=({\overrightarrow{u}}_1,{\overrightarrow{u}}_2,...,{\overrightarrow{u}}_n)$，是$L$的单位特征向量构成的矩阵。

为什么要对拉普拉斯矩阵进行谱分解呢？

在信号与系统中我们知道，连续信号的傅里叶变换的公式为：
$$F(w)=\mathcal{F}[f(x)]={\int }_{-\infty }^{\infty }f(x)e^{-iwx}\mathrm{d}x\text{\hspace{1em}(4)}$$
或者离散信号的傅里叶变换为：
$$X(k)=\sum _{n=0}^{N-1}x(n)e^{-j\frac{2\pi }{N}kn},k=1,2,...,N-1\text{\hspace{1em}(5)}$$
可以看到，信号从时域转换到频域其实可以看作是把时域信号与频域的基底进行内积运算，或者说是把时域信号用频域的基底线性表示。而对拉普拉斯矩阵进行谱分解就是为了找到这些基底，并构成一个映射矩阵$U$。

3.2 图的傅里叶变换(Graph Fourier Transform)

现直接给出图傅里叶变换的定义，对于图$f$，其傅里叶变换可以写成：
$$\hat{f}=U^{T}f\text{\hspace{1em}(6)}$$
图的反傅里叶变换为：
$$f=U\hat{f}\text{\hspace{1em}(7)}$$

3.3 图卷积之Spectral GCN

在上面的基础上，给出图f与卷积核g的卷积公式：
f ∗ g = F − 1 { F ( f ) ⋅ F ( g ) } = F − 1 ( f ^ ⋅ g ^ ) (8) f * g = {\mathcal{F}^{-1}} \lbrace {\mathcal{F}} (f) \cdot {\mathcal{F}} (g) \rbrace = {\mathcal{F}^{-1}} (\hat{f} \cdot \hat{g}) \tag{8} f∗g=F−1{F(f)⋅F(g)}=F−1(f^​⋅g^​)(8)
所以图f与卷积核g可以写成：
$${(f\ast g)}_G=U((U^{T}g)\odot (U^{T}f))=U(\theta \odot U^{T}x)=U{g}_{\theta }{U}^{T}x,g_{\theta }=diag(\theta )\text{\hspace{1em}(9)}$$
把$g_{\theta }$看作是一个可以学习参数$g_{\theta }={\Theta }_{i,j}^k$，那么图卷积层可以写成：
$$X_{:,j}^{k+1}=\sigma (\sum _{i=1}^{f_{k-1}}U{\Theta }_{i,j}^k{U}^T{X}_{:,i}^k)(j=1,2,..,f_k)\text{\hspace{1em}(10)}$$

• $X_k\in {\mathbb{R}}^{N\times f_{k_1}}$是输入图像，对应图上的点输入特征；
• $N$是结点数量；
• $f_{k-1}$是输入通道的数量；
• $f_k$是输出通道的数量；
• ${\Theta }_{i,j}^k$是可学习的参数；
• $\sigma (\cdot )$是激活函数。

这样提出的图卷积存在很大的弊端，主要包括：

• 计算复杂度太大。每一次前向传播都要计算出$U$，$diag({\theta }_l)$，$U^T$及三者的乘积，这需要的时间复杂度为$O(N^2)$；
• 参数太多。卷积核需要$N$个参数；
• 是非局部连接的。

3.4 图卷积之Chebyshev GCN

为了降低计算复杂度，人们还提出了ChebNet。由公式(9)可以知道：
$$g_{\theta }\ast x=U{g}_{\theta }{U}^{T}x\text{\hspace{1em}(11)}$$

• U是对称归一化拉普拉斯矩阵$L^{sys}=D^{-\frac{1}{2}}L{D}^{\frac{1}{2}}=I-D^{-\frac{1}{2}}A{D}^{\frac{1}{2}}$的特征向量矩阵；
• $U^{T}x$是x的傅里叶变换；
• $g_{\theta }$是由参数$\theta$构成的对角矩阵$diag(\theta )$，所以可以把$g_{\theta }$看作是特征值$\Lambda$的一个函数，即令$g_{\theta }=g_{\theta }(\Lambda )$。

定义$g_{\theta }(\Lambda )$的切比雪夫多项式为滤波器，即：
$$g_{\theta }(\Lambda )\approx \sum _{k=0}^{K-1}{\theta }_k{T}_k(\tilde{\Lambda })\text{\hspace{1em}(12)}$$

• $\tilde{\Lambda }=\frac{2}{{\lambda }_{max}}\Lambda -I_N$，${\lambda }_{max}$是$L$的最大特征值，也叫谱半径；
• ${\theta }_k\in {\mathbb{R}}^K$是切比雪夫系数向量；
• 切比雪夫多项式递归定义为$T_k(x)=2x{T}_{k-1}(x)-T_{k-2}(x)$，其中$T_0(x)=1,T_1(x)=x$

所以图的卷积可以写成：
$$g_{\theta }\ast x=\sum _{k=0}^K{\theta }_k{T}_k(\tilde{L})x\text{\hspace{1em}(13)}$$

• $\tilde{L}=\frac{2L}{{\lambda }_{max}}-I_N=U\tilde{\Lambda }{U}^T$

Chebyshev GCN其实就是使用切比雪夫多项式拟合卷积核的方法。相比于Spectral GCN，ChebNet做到了：

• K-localized。即具有局部连接性；
• $T_k(\tilde{L})$现在的计算复杂度为$O(|E|)$。

3.5 图卷积之GCN

由于L的最大特征值近似取2，因此1阶图卷积可以写成：
$$g_{\theta }\ast x\approx {\theta }_{0}x+{\theta }_1(L-I_N)x={\theta }_{0}x-{\theta }_1{D}^{-\frac{1}{2}}A{D}^{\frac{1}{2}}x\text{\hspace{1em}(14)}$$
为了进一步减少参数，上式还可以写为：
$$g_{\theta }\ast x\approx \theta (I_N+D^{-\frac{1}{2}}A{D}^{\frac{1}{2}})x,\theta ={\theta }_0={\theta }_1\text{\hspace{1em}(15)}$$
上式括号中$I_N+D^{-\frac{1}{2}}A{D}^{\frac{1}{2}}$的特征值在$[0,2]$中，可以采用归一化：
$$I_N+D^{-\frac{1}{2}}A{D}^{\frac{1}{2}}\to {\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{\frac{1}{2}},\tilde{A}=A+I_{N}and{\tilde{D}}_{ii}=\sum _j{\tilde{A}}_{ij}\text{\hspace{1em}(16)}$$
再加上激活函数，即可得到GCN：
$$H^{(l+1)}=f(H^l,A)=\sigma ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{\frac{1}{2}}{H}^l{W}^l)\text{\hspace{1em}(17)}$$

• $W^l$是参数$\theta$的参数矩阵。

4. 空间域图卷积(Spatial Convolution)

基于空间的图卷积是基于节点空间关系来的定义卷积的。为了将图像与图关联起来，可以将图像视为图的特殊形式，每个像素代表一个节点，如下图a所示，每个像素直接连接到其附近的像素。通过一个3×3的窗口，每个节点的邻域是其周围的8个像素。这八个像素的位置表示一个节点的邻居的顺序。然后，通过对每个通道上的中心节点及其相邻节点的像素值进行加权平均，对该3×3窗口应用一个滤波器。由于相邻节点的特定顺序，可以在不同的位置共享可训练权重。同样，对于一般的图，基于空间的图卷积将中心节点表示和相邻节点表示进行聚合，以获得该节点的新表示。

5. 总结

本文主要介绍了GNN中的GCN，其中GCN根据卷积的方法可以分为基于空间的与基于频域的。GNN除了GCN外还有图注意力网络(Graph Attention Networks)、图自编码器(Graph Autoencoders)、图生成网络(Graph Generative Networks)和图时空网络(Graph Spatial-temporal Networks)。

参考文献(Reference)

Kip F T N , Welling M . Semi-Supervised Classification with Graph Convolutional Networks[J]. 2016.

图神经网络（Graph Neural Networks，GNN）综述

图卷积网络 GCN Graph Convolutional Network（谱域GCN）的理解和详细推导

【离散数学】图论（一）图的基础知识

图卷积网络 GCN Graph Convolutional Network（谱域GCN）的理解和详细推导

【离散数学】图论（一）图的基础知识

学好GNN第一课：Spectral GCN、Chebyshev GCN、GCN（ICLR 2017）

版权声明

转载请注明出处。