基础知识1：Jones matrix

 一、 假设Jones matrix 为：

   则输出电场和输入电场的关系为：

   其中T具有对称性和酉性

    因此，对于正输入光波的输入输出电场的关系为：

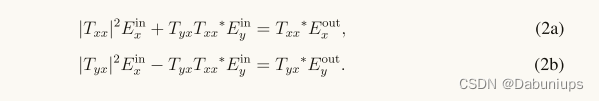
     两式子相加：

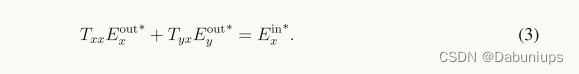
     其中: Ex 和 Ey 为电场的 x 分量和 y 分量， 表示复共轭  

     从 (1a) 和 (3) 可得：

       因此，通过给定Ein 和 Eout，我们可以得到 Txx 和 Txy，并且结合对称性和酉性条件可计算 Txy和Tyy

       当 (4)  式左侧矩阵行列式为 0 时，则

       考虑亚波长结构将两个独立的相位分布强加于两个正交偏振的光波上，的情况，入射光场与出射光场可以描述为：

       其中，phi 1 和 phi 2为任意的附加相位。当存在一组正交的偏振光时，可以认为亚波长结构在一组正交偏振入射下实现了两种不同的相位分布

       给定任意一组正交偏振的入射光Ein1 和 Ein2 , 以及出射场 Eout1 和 Eout2，可以唯一确定琼斯矩阵，可以实现正交偏振的独立调控。

       二、 Jones Matrix

        其中，Jij 表示光学器件的复转换系数，模值表示振幅大小，角度值表示相位变化。下标 ij 表示入射光 i 分量转化为出射光 j 分量。

       三、多通道调制Jones Matrix

        1、双通道调制

              假设入射 x、y 偏振光

         2、三通道调制 (旋转琼斯矩阵)

              假设入射 x、y 偏振光

              phi3 = 2*phi2 - phi1 + pi 

               圆偏振光入射