MVRPTW

一、问题简介

MTVRPTW问题，该问题的图论描述如下：$G(N,A)$表示一个无向图， N = { 0 , 1 , ⋅ ⋅ ⋅ , n } N=\{0,1,\cdot\cdot\cdot,n\} N={0,1,⋅⋅⋅,n}表示无向图的节点集合，节点0表示中心货物配送中心，是车辆出发和返回地点，要求所有的车辆从配送中心出发，最后回到配送中心，每辆车可以跑多个车程；节点$1,\cdot \cdot \cdot ,n$表示客户节点，每个客户$i\in N$有货品配送需求量$q_i$，每两个节点之间有两条弧线相连， A = { ( i , j ) ∣ i , j ∈ N ; i ≠ j } A=\{(i,j)|i,j\in N;i\neq j\} A={(i,j)∣i,j∈N;i​=j}表示所有弧的集合， c i j { i , j ∈ N ; i ≠ j } c_{ij}\{i,j\in N;i\neq j\} cij​{i,j∈N;i​=j}表示节点之间的配送成本，通常用两点之间的欧式距离表示，且$c_{ij}=c_{ji}$，假设配送中心有$m$辆同类型的配送车辆，每辆车的核定载重为$Q$。

配送中心和客户均有时间窗限制，配送中心的时间窗为$[e_0,l_0]$，即车辆只能在$e_0$之后（包含$e_0$）离开，且只能在$l_0$之前（包含$l_0$）返回。对于编号为$i$的客户也有预先设定的时间窗$[e_i,l_i]$，车辆为客户$i$提供的时间必须在此区间内。此外客户$i$有需求准备时间$prepareTim{e}_i$，即当配送中心接到客户$i$的订单后，准备完成时间为$prepareTim{e}_i$，这意味着若车辆要配送客户$i$的订单，那么只能在$prepareTim{e}_i$之后才能开始配送。

MTVRPTW问题是传统VRP问题的拓展，在VRP问题的基础上考虑了节点的时间窗、车辆容量以及车辆能够行驶多车程的问题，如下图所示：

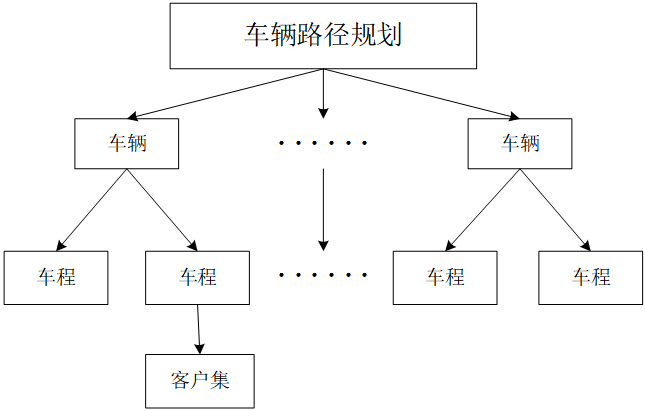
该问题的目标通常包含配送里程最小（即所有车程的里程之和最小），最小化车辆的使用数（每多使用一辆车就需要多增加一辆车的固定资产投入），最大化客户满意度（尽量满足客户的需求且在客户的时间窗范围提供服务）。

二、模型假设

(1) 仅考虑一个派单网点（即一个配送中心）；

(2) 服务不可拆分，每个客户点只能由一辆车在一条回路中提供服务；

(3) 每条回路从配送中心开始，到配送中心结束；

(4) 车辆需要在客户的时间窗内提供服务；

(5) 每条回路覆盖的客户需求量不能超过车辆的运载能力；

(6) 所有客户订单信息已知，暂不考虑实时单；

(7)不考虑客户点的服务时间；

(8)车辆匀速行驶；

三、符号设定

决策变量

四、数学模型

目标函数:最小化总配送里程

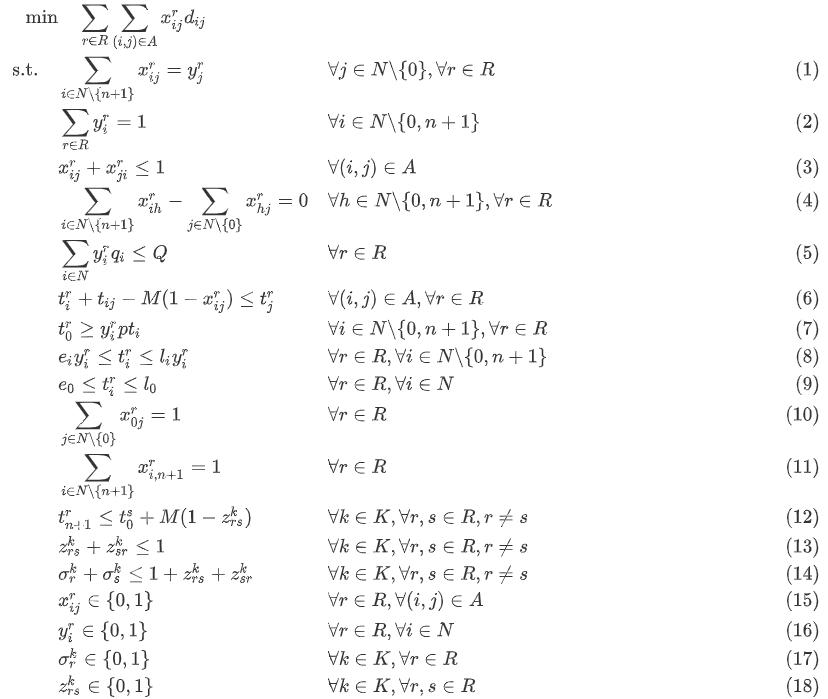
• 约束（1）如果配送中心在回路$r$上为客户$j$提供服务，那么客户$j$之前最多一个前置节点；
• 约束（2）每一个客户节点仅被服务一次；
• 约束（3）每一条回路都是单向的；
• 约束（4）流守恒，有进必有出，进出必相等；
• 约束（5）每一条回路上覆盖的总需求不能超过车辆的运载能力；
• 约束（6）消除子回路；
• 约束（7）每一条回路的车辆的出发时间必须晚于这条回路覆盖的所有客户的需求准备完成时间；
• 约束（8）（9）时间窗约束；
• 约束（10）（11）每一条回路必须从配送中心出发到配送中心结束；
• 约束（12-14）回路分配约束；
• 约束（15-18）0-1变量约束；

五、算法设计

5.1 编码设计

节点编码设计：

采用自然数编码，0表示配送中心，【1,2，······，n】表示客户点。

解的编码设计：

解是A*B的二维矩阵,其中A是车辆数$A=|K|$

$B$=仅有一辆车时采用启发式算生成初始解时的路径点数

5.2 初始解的生成

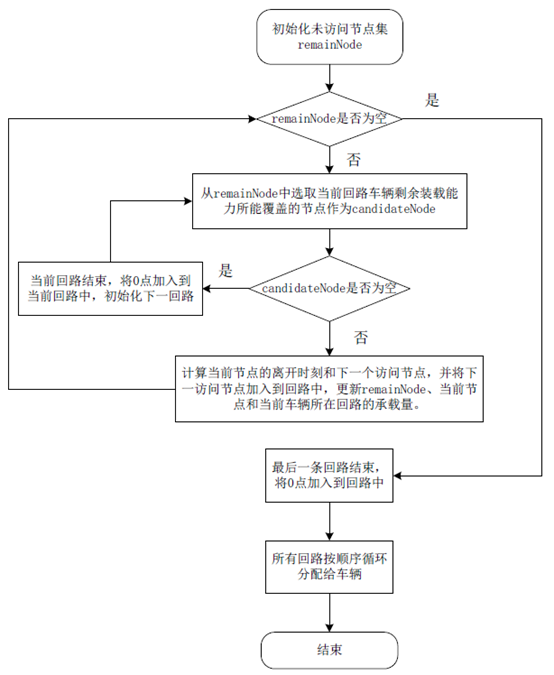
Step1: 初始化未访问节点集 remainNode = 【1,2，······，n】；

Step2: 从未访问节点集remainNode中选择车辆在当前回路的剩余装载能力能够覆盖的节点，作为候选节点集candidateNode。若candidateNode不为空则执行Step3，否则执行Step5；

Step3: 计算当前节点的离开时刻和下一个访问节点，并将下一访问节点加入到回路中，从remainNode中删除该节点，更新当前节点、和当前车辆所在回路的承载量。

Step4: 若remainNode不为空则执行Step2，否则执行Step6；

Step5: 当前回路结束，将0点加入到当前回路中（即回到配送中心），初始化下一回路车辆承载能力，返回Step2；

Step6: 最后一条回路结束，将0点加入到回路中；

Step7: 将所有回路按照顺序循环分配给所有车辆形成初始解。

算法流程图

$$candidateD{T}_j=max(R{T}_j,E{T}_j-t_{ij})i=currentNode,\forall j\in candidateNode$$

**注：**当前节点的离开时刻 = min(max(候选节点需求的准备完成时刻，前一节点到达当前节点的时刻，候选节点的最早服务时间-从当前节点到候选节点的旅行时间))

c u r r e n t D T i = m a x ( A T i , m i n ( { c a n d i d a t e D T j ∣ ∀ j ∈ c a n d i d a t e N o d e } ) ) currentDT_{i} =max (AT_i, min(\{candidateDT_j|\forall j \in candidateNode\})) currentDTi​=max(ATi​,min({candidateDTj​∣∀j∈candidateNode}))

$$nextNode={\mathrm{argmin}}_{j}candidateD{T}_j,\forall j\in candidateNode$$

• $R{T}_j$:订单$j$的需求准备完成时间

• $A{T}_i$:当前节点$i$的到达时间

• $t_{ij}$:当前节点$i$到候选节点$j$的旅行距离

• nextNode:下一个访问节点

**例 1:**当前有3辆车负责7个客户点的配送，经过Step1-Step5之后的所有回路为【0-1-0-2-0-3-4-0-5-0-6-0-7-0】

则循环分配给3辆车后形成的初始解为：
$$\left[\begin{array}{cccccccccccccc}0& 1& 0& 5& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 2& 0& 6& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 3& 4& 0& 7& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$
**含义：**第一辆车行驶顺序为从配送中心到客户点1再回到配送中心到客户点2最后再回到配送中心。

5.3 邻域设计

destroy函数设计

Step1: 将车辆的行驶路径按其配送成本降序排列；

Step2: 从前往后选取车辆覆盖客户点作为候选破坏点集，直到候选点个数大于等于破坏点数（$destroyNum\ge 1$）；

Step3: 从候选点集中随机选择destroyNum个候选点作为破坏点，输出破坏后的不完整解及其破坏点集合。

同例1：

当前解为：
$$\left[\begin{array}{cccccccccccccc}0& 1& 0& 5& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 2& 0& 6& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 3& 4& 0& 7& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$
假设破坏点的个数为1，车辆的行驶路径按其配送成本降序排列后的解为
$$\left[\begin{array}{cccccccccccccc}0& 3& 4& 0& 7& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 2& 0& 6& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 5& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$
则候选破坏点集为【3、4、7】，从中随机选择一个点作为候选点。

假设选中的破坏点为7，则破坏后的不完整解为
$$\left[\begin{array}{cccccccccccccc}0& 3& 4& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 2& 0& 6& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 5& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$

repair函数设计

将破坏的点插入到经destroy函数处理后的不完整解中。有多种插入方法，选取其中neighborhoodSize个插入方法构成邻域。从邻域中选择总配送成本最小的解作为新解。

同上例1：将破坏点7插入到破坏后的不完整解中有多种插入方式，如下【】表示的是其有效插入位置，则破坏点7有16种插入方式，每一种插入方式作为邻域中的一个解。每一行其余的0位和该行最后一个【】效果等价，因此我们去除掉重复情况。
$$\left[\begin{array}{cccccccccccccc}0& 【】& 【】& 【】& 【】& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 【】& 【】& 【】& 【】& 【】& 【】& 0& 0& 0& 0& 0& 0& 0\\ 0& 【】& 【】& 【】& 【】& 【】& 【】& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$$

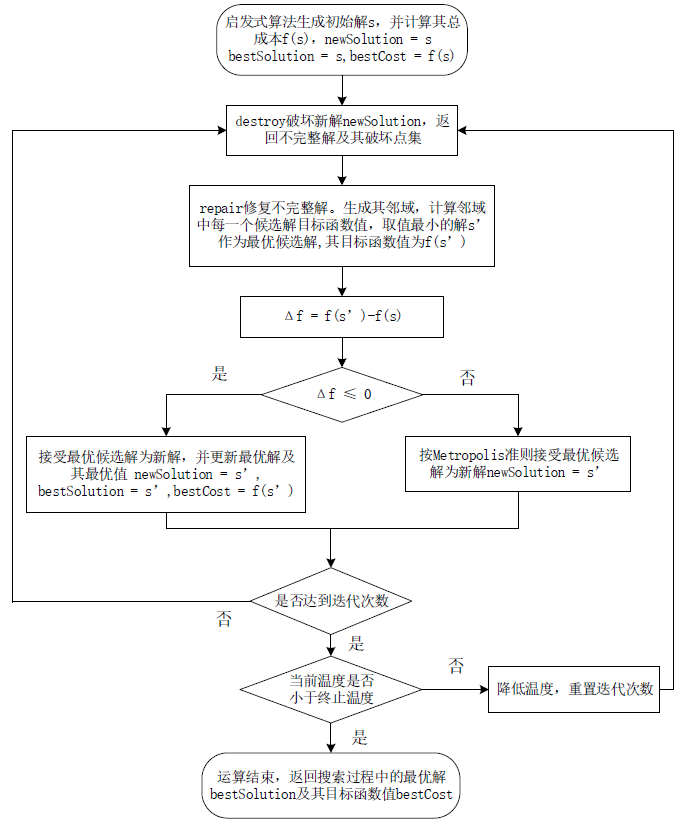
5.4 算法总框架

六、算例测试

参数输入：

节点数：$N=30$

车辆数量：$vehicleNr=3$

车辆容量：$Q=12e6c{m}^3$

车辆行驶速度：$speed=1km/min$

邻域空间大小：$neighborhoodSize=50$

破坏率：$destroyration=0.15$

初始温度：$T=100$

最低温度：$Tfloor=1$

降温系数：$\alpha =0.8$

每一温度下的迭代次数：$iterCount=100$

==注：==配送成本 = $\alpha$总配送里程+$\beta$总超时+$\gamma$总超载量,在此次实验中选取$\alpha =1$，$\beta =10$，$\gamma =20$

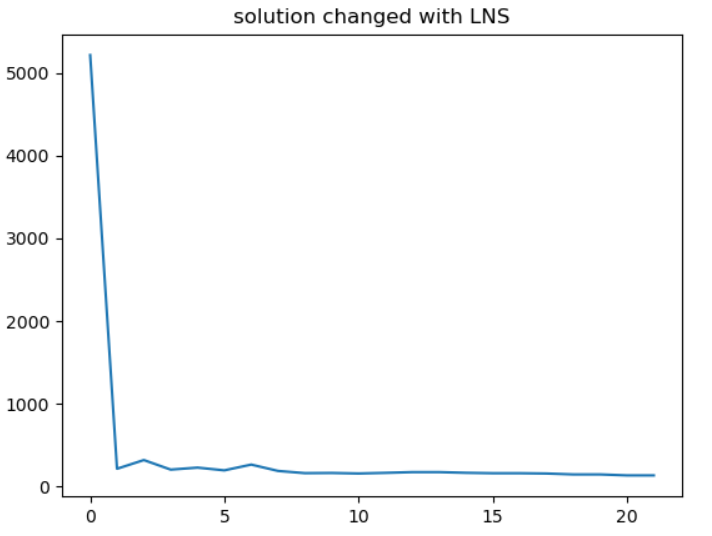
算例求解结果

结果解释

运行时间耗费41.92秒，配送成本为131；

第一辆车的运行路线：【0-6-9-2-22-18-20-19-1-15-5-4-28–13-23-17-11-8-29-12-0】；

第二辆车的运行路线：【0-10-21-16-3–25-26-24-27-14-7-0】；

第三辆车没有被使用。

迭代过程图

七、参考文献

---

[1]吴球军. 带硬时间窗的外卖配送车辆路径问题研究[D].集美大学,2020.

[2]袁晓建,张岐山,吴伶,江义火.带时间窗和同时送取货的车辆路径问题模型及算法[J/OL].福州大学学报(自然科学版):1-7[2020-10-19].

[3]Binbin Pan, Zhenzhen Zhang, Andrew Lim,Multi-trip time-dependent vehicle routing problem with time windows,European Journal of Operational Research,2020,ISSN 0377-2217.

[4]Philippe Grangier, Michel Gendreau, Fabien Lehuédé, Louis-Martin Rousseau,An adaptive large neighborhood search for the two-echelon multiple-trip vehicle routing problem with satellite synchronization,European Journal of Operational Research,Volume 254, Issue 1,2016,Pages 80-91,ISSN 0377-2217.

Fabien Lehuédé, Louis-Martin Rousseau,An adaptive large neighborhood search for the two-echelon multiple-trip vehicle routing problem with satellite synchronization,European Journal of Operational Research,Volume 254, Issue 1,2016,Pages 80-91,ISSN 0377-2217.