地震勘探原理（六）之地震组合方法原理

本文链接：https://blog.csdn.net/qq_41033011/article/details/110891396

本文探讨了地震勘探中的干扰波特点及处理方法，分析了简单线性组合的方向特性，并介绍了地震组合的其他特性，包括随机干扰的统计特性及组合频率特性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

一、地震勘探中的干扰波特点

1. 有效波（反射的P波）和干扰波（面波）的差别

传播方向上可能不同。例如水平界面的反射波差不多是垂直从地下反射回地面的；而面波是沿地面传播的。实质上就是视速度的差别。针对这一类型的干扰波，在野外施工时，往往采用检波器组合的方法来压制；在进行资料处理时，还可以采用视速度滤波（f-k滤波）进行去除。
有效波和干扰波可能在频谱上有差别。此类干扰波的压制方法主要是野外记录时进行有目的的采取滤波和室内的频率滤波处理。
有效波和干扰波经过动校正后的剩余时差可能有差别。如多次波，在经过动校正后，剩余时差仍不为 0，如今广泛使用的野外多次覆盖、室内水平叠加技术能较好的压制多次波；另外，预测反褶积方法对多次波也有良好的压制效果。
有效波和干扰波在它们出现的规律上可能有差别。例如风吹草动等引起的随机干扰的出现规律就与反射波的很不相同。对于随机干扰，主要是利用其统计规律进行压制，如多次叠加、组合法等都是有效的方法。另外，相关滤波、相干叠加等室内处理方法也有很好的效果。

我们所追求的地震资料的三高：信噪比、分辨率和保真度。

二、简单线性组合的方向特性

1. 组合的概念

组合（array）：指一组检波器将信号输出到同一地震道，或同时激发一组震源，有时也称组合形式（pattern）。

2. 组合的实现

野外检波器组合
野外震源组合
室内混波：若干个地震道讯号按比例相加，形成新的地震道

下列有9个检波器等间距的放置如下：
在这里插入图片描述

3. 组合的类型

简单线性组合：
- 若干个检波器沿直线等距排列
- 各检波器灵敏度相同
加权组合：各点检波器的灵敏度不同
面积组合

在这里插入图片描述

4. 组合的目的

增强有效波，压制干扰波，提高信噪比

对于规则干扰波，组合具有方向性，对不同方向来的波，具有不同的灵敏度
对于随机干扰，也可压制

5. 简单线性组合的特性

研究已知条件：
- $n$ 个检波器线性排列，组内距 $Δ x$
- 地震波为平面波，波前与地面的夹角为 $α$ ，即地震波到达相邻检波器的时差为： $Δ t = Δ x s i n α / V$

在这里插入图片描述

下面我从数学的角度来研究足额和输出信号与单个检波器信号的关系。
在这里插入图片描述

求解思路：组合可以看成一个滤波系统，单个检波器的信号看成是滤波系统的输入，组合后的结果为滤波系统的输出。假设在时间域中单个检波器的信号为 $f (t)$ ，它的傅里叶变换为 $F (j ω)$ ， $f (t)$ 和 $F (j ω)$ 两者互为傅里叶的正常变换。如果我们将简单线性组合看作一个系统的话，那么这个系统特性记作 $k (t)$ ，对应的傅里叶变换为 $K (j ω)$ 。同样的，这个检波器组合之后，它的输出为 $g (t)$ ，其对应的傅里叶变换为 $G (j ω)$ 。
在这里插入图片描述

这两者之间在时间域上是褶积的关系，在频率域中是乘积的关系（褶积定理）。即满足下列关系式：
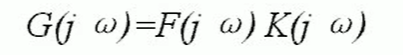
在这里插入图片描述
那么我们要求出检波器组合的特性（ $K (j ω)$ ），即：

那么现在的问题就是输入的谱和输出的谱怎么求解的问题。有了这两者，直接相比，就可以得到组后之后的特性。

6. 组合特性分析

对于给定的 $Δ t$ （相邻检波器的旅行时差），组合相当于一个频率滤波器。
输入简谐波，组合输出也为简谐波，其相位与检波器组中心处振动的相位相同，相当于第一个检波器的输出在时间上延迟 $t = Δ t (n - 1) / 2$
- $n$ 为奇数时与中间检波器相同
- $n$ 为偶数时为中间两个检波器的平均
$Δ t$ 是由波的传播方向决定的，故 $K (j ω)$ 应写成 $K (j ω, Δ t)$ ，称为组合的频率特性，若令 $Δ Φ = - ω Δ t$ ，则可得到组合方向频率特性的另一种表达式。

7. 组合响应：

定义：组合输出振幅与单个检波器输出振幅 $n$ 倍（或 $n$ 个检波器置于一点的输出振幅）的比值。
组合响应：

下面是分析推导过程：
组合曲线：对于给定速度 $V$ 和 $n$ 和 $Δ x$ ，可作出 $Φ (n, Δ t / T)$ 的图形，称为组合的方向特性曲线，即：

5. 通过带和压制带
在这里插入图片描述

6. 组合对信噪比的影响（方向效应）

一般要求信噪比提高 $n$ 倍

三、地震组合的其他特性

一、随机干扰的统计特性

没有一定规律，也没有一定传播方向，在地震记录上形成杂乱无章的干扰背景。形成因素很多：自然条件、激发条件、人为条件。

1. 随机干扰的特点

在地震记录上表现为杂乱无章的振动，频谱很宽，近似于白噪声，没有一定的视速度，表面上看是不规则的，但遵循统计规律。
白噪声：对一个信号做频谱分析，若所有频率成份的振幅均近似相等，如同白光一样，称为白噪声。
地震勘探中的随机干扰是具有各态历经性质的平稳、随机过程，其统计性质不随时间改变，只需几个统计参数就可以描述这个随机过程。

地震勘探中在某一点记录下来的随机干扰是一个随机函数 $n (t)$ 。重复放炮，记录下的随机干扰各不相同（n1(t) != n2(t) != n3(t)…）。

随机过程：所有可能的随机函数的集合。其次观测的随机函数称为随机过程的一个实现。

平稳随机过程：统计规律不随时间变化的随机过程。即对随机过程的一次实现，只需研究足够长的一段时间即可获得该次实现的其统计规律。

各态历经性质：一个随机过程的统计规律不必从多次实现中求得，只需从一次实现便可求得。即一次实现能反映随机过程的全部特点。

2. 描述随机过程的参数

平均值：地震勘探中随机干扰的平均值为零
方差：描述随机过程偏离平均值幅度的量
自相关函数：描述随机过程变化快慢的量

对于平均值为零的随机过程，只需用自相关函数这一个统计参数就可以充分描述其统计特性。

3. 随机干扰的压制方法

组合法和共中心点叠加法可以压制随机干扰

压制原理：

随机干扰的相干半径
压制原理
多次覆盖由于组合

由于组合法是同一时间不同位置上振动的叠加，所以只研究在位置上的相关性就够了。任意两个检波点之间波形的相似程度是用相关系数表示的，若在某距离上不规则波（随机干扰）互不相似，我们称此距离为相关半径。
一般结论是，当组内距大于随机干扰的相关半径时，经过组合以后，有效波相对于随机干扰的信噪比要提高 $n^{1/2}$ 倍。