软阈值(Soft Thresholding)函数

1. 软阈值(Soft Thresholding)函数的作用

  软阈值(Soft Thresholding)可以求解如下优化问题：
      $\underset{x}{\mathrm{argmin}}\Vert X-B{\Vert }_2^2+\lambda \Vert x{\Vert }_1$
  其中：
      $X=[x_1,x_2,\dots ,x_N{]}^T$
      $B=[b_1,b_2,\dots ,b_N{]}^T$

  根据范数的定义，可以将上面优化问题的目标函数拆开：

  $$\begin{gathered} F(X)=\Vert X-B{\Vert }_2^2+\lambda \Vert X{\Vert }_1 \\ =[(x_1-b_1{)}^2+\lambda \Vert x_1\Vert ]+[(x_2-b_2{)}^2+\lambda \Vert x_2\Vert ]+\cdots +[(x_N-b_N{)}^2+\lambda \Vert x_N\Vert ] \end{gathered}$$

  也就是说，我们可以通过求解 $N$ 个独立的形如函数

      $f(x)=(x-b{)}^2+\lambda |x|$

的优化问题，来求解这个问题。由中学时代学过的求极值方法知道，可以求函数 $f(x)$ 导数：

      $\frac{df(x)}{dx}=2(x-b)+\lambda \text{sgn}(x)$
      $\text{sgn}(x)=1,x>0$
      $\text{sgn}(x)=-1,x<0$

  这里解释一下变量 $x$ 绝对值的导数，当 $x>0$ 时，$|x|=x$，因此其导数等于 1；当 $x<0$ 时，$|x|=x$，因此其导数等于 -1；综合起来，$x$ 绝对值的导数等于 $\text{sgn}(x)$。令函数 $f(x)$ 导数等于 0，得：
      $x=b-\frac{\lambda }{2}\text{sgn}(x)$

  这个结果等号两端都有变量 $x$，需要再化简一下。下面分三种情况讨论：

1. 当 $b>\lambda /2$ 时

假设 $x<0$，则 $\text{sgn}(x)=-1$，所以 $x=b+\lambda /2>0$，与假设 $x<0$ 矛盾；
假设 $x>0$，则 $\text{sgn}(x)=1$，所以 $x=b-\lambda /2>0$，成立；

  所以此时在 $x=b-\lambda /2>0$ 处取得极小值：

$$\begin{gathered} f(x){|}_{x=b-\lambda /2}=(b-\frac{\lambda }{2}-b{)}^2+\lambda (b-\frac{\lambda }{2}) \\ =b\lambda -\frac{{\lambda }^2}{4} \\ =-(\frac{\lambda }{2}{)}^2+2b\frac{\lambda }{2} \\ =-(\frac{\lambda }{2}{)}^2+2b\frac{\lambda }{2}-b^2+b^2 \\ =-(\frac{\lambda }{2}-b{)}^2+b^2<b^2=f(0) \end{gathered}$$

  即此时极小值小于 $f(0)$，而当 $x<0$ 时

$$\begin{gathered} \frac{df(x)}{dx}=2(x-b)+\lambda \text{sgn}(x) \\ =2x-2b-\lambda \\ <2x-2(\frac{\lambda }{2})-\lambda \\ =2x-2\lambda <0 \end{gathered}$$

  即当 $x<0$ 时函数 $f(x)$ 为单调降函数 (对任意 $\Delta x<0,f(0)<f(\Delta x)$)。因此，函数在 $x=b-\frac{\lambda }{2}>0$ 处取得最小值。

---

2. 当 $b<\lambda /2$ 时

假设 $x<0$，则 $\text{sgn}(x)=-1$，所以 $x=b+\lambda /2<0$，成立；
假设 $x>0$，则 $\text{sgn}(x)=1$，所以 $x=b-\lambda /2<0$，与假设 $x<0$ 矛盾；

  所以此时在 $x=b+\lambda /2<0$ 处取得极小值：

$$\begin{gathered} f(x){|}_{x=b+\lambda /2}=(b+\frac{\lambda }{2}-b{)}^2+\lambda (b+\frac{\lambda }{2}) \\ =-b\lambda -\frac{{\lambda }^2}{4} \\ =-(\frac{\lambda }{2}{)}^2-2b\frac{\lambda }{2} \\ =-(\frac{\lambda }{2}{)}^2-2b\frac{\lambda }{2}-b^2+b^2 \\ =-(\frac{\lambda }{2}+b{)}^2+b^2<b^2=f(0) \end{gathered}$$

  即此时极小值小于 $f(0)$，而当 $x>0$ 时

$$\begin{gathered} \frac{df(x)}{dx}=2(x-b)+\lambda \text{sgn}(x) \\ =2x-2b+\lambda \\ >2x-2(-\frac{\lambda }{2})+\lambda \\ =2x+2\lambda >0 \end{gathered}$$

  即当 $x<0$ 时函数 $f(x)$ 为单调降函数 (对任意 $\Delta x<0,f(0)<f(\Delta x)$)。因此，函数在 $x=b-\frac{\lambda }{2}>0$ 处取得最小值。

---

3. 当 $-\frac{\lambda }{2}<b<\frac{\lambda }{2}$ 时

假设 $x<0$，则 $\text{sgn}(x)=-1$，所以 $x=b+\lambda /2>0$，与假设 $x<0$ 矛盾；
假设 $x>0$，则 $\text{sgn}(x)=1$，所以 $x=b-\lambda /2<0$，与假设 $x>0$ 矛盾；

  即无论 $x$ 为大于 0 还是小于 0 均没有极值点，那么 $x=0$ 是否为函数 $f(x)$ 的极值点呢？

对于 $\Delta x\ne 0$

$$\begin{gathered} f(\Delta x)=(\Delta x-b{)}^2+\lambda |\Delta x| \\ =(\Delta x{)}^2-2\Delta xb+b^2+\lambda |\Delta x| \\ =(\Delta x{)}^2-2\Delta xb+\lambda |\Delta x|+f(0) \end{gathered}$$

当 $\Delta x>0$ 时，利用条件 $b<\frac{\lambda }{2}$ 可得

$$\begin{gathered} f(\Delta x)=(\Delta x{)}^2+2\Delta xb+\lambda \Delta x+f(0) \\ >(\Delta x{)}^2-2\Delta x\frac{\lambda }{2}+\lambda \Delta x+f(0) \\ =(\Delta x{)}^2+f(0)>f(0) \end{gathered}$$

当 $\Delta x<0$ 时，利用条件 $b<\frac{\lambda }{2}$ 可得

$$\begin{gathered} f(\Delta x)=(\Delta x{)}^2-2\Delta xb+\lambda |\Delta x|+f(0) \\ >(\Delta x{)}^2-2\Delta x\frac{\lambda }{2}+\lambda |\Delta x|+f(0) \\ =(\Delta x{)}^2+\lambda (-\Delta x)+\lambda |\Delta x|+f(0) \\ =(\Delta x{)}^2+2\lambda |\Delta x|+f(0)>f(0) \end{gathered}$$

  因此，函数在 $x=0$ 处取得最小值。
  综合以上三种情况，$f(x)$ 的最小值在以下位置取得：

$\text{argmin}f(x)=\{\begin{array}{ll}b+\frac{\lambda }{2}& ,b<-\frac{\lambda }{2}\\ 0& ,|b|<\frac{\lambda }{2}\\ b-\frac{\lambda }{2}& ,b>\frac{\lambda }{2}\end{array}$

  与前面的软阈值(Soft Thresholding)对比一下，发现了么？若将上式中的 $b$ 视为变量，$\frac{\lambda }{2}$ 视为阈值，上式即为软阈值 (SoftThresholding) 的公式。

  至此，我们可以得到优化问题

      $\underset{x}{\mathrm{argmin}}\Vert X-B{\Vert }_2^2+\lambda \Vert X{\Vert }_1$
的解为

$\text{soft}(B,\frac{\lambda }{2})=\{\begin{array}{ll}B+\frac{\lambda }{2}& ,B<-\frac{\lambda }{2}\\ 0& ,|B|<\frac{\lambda }{2}\\ B-\frac{\lambda }{2}& ,B>\frac{\lambda }{2}\end{array}$

注：该式为软阈值(Soft Thresholding)的矩阵形式。

---

2. 软阈值(Soft Thresholding) 的变形

  当优化问题变为

      $\underset{x}{\mathrm{argmin}}\frac{1}{2}\Vert X-B{\Vert }_2^2+\lambda \Vert X{\Vert }_1$

  因为对目标函数乘一个常系数不影响极值点的获得，所以可等价为优化问题

      $\underset{x}{\mathrm{argmin}}\Vert X-B{\Vert }_2^2+2\lambda \Vert X{\Vert }_1$

  此时的解为 $soft(B,\lambda )$。

---

3. 软阈值(Soft Thresholding)的MATLAB代码

  软阈值(Soft Thresholding)的函数代码可以写成专门针对问题

      $\underset{x}{\mathrm{argmin}}\Vert X-B{\Vert }_2^2+\lambda \Vert X{\Vert }_1$

  软阈值(Soft Thresholding)是如此简单以至于可以用一句代码去实现它：

  

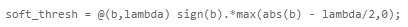
  当然，也可写为另一种形式：

function [soft_thresh] = softthresholding(b, lambda)
	soft_thresh = sign(b).*max(abs(b) - lambda/2, 0);
end

python 代码：

# Soft Thresholding
def softthresholding(b, lam):
    soft_thresh = sign(b) * max(abs(b) - lam//2, 0)
    return soft_thresh

一定要注意：这种写法是针对最开始的优化问题：

$\underset{x}{\mathrm{argmin}}\Vert X-B{\Vert }_2^2+\lambda \Vert X{\Vert }_1$

只需调用 softthresholding($B,\frac{\lambda }{2}$) 即可。

若要解决优化问题

$\underset{x}{\mathrm{argmin}}\Vert X-B{\Vert }_2^2/2+\lambda \Vert X{\Vert }_1$

只需调用 softthresholding($B,\lambda$) 即可。

---

4. 软阈值(Soft Thresholding)测试代码

  用以下一小段代码测试软阈值，用来求解优化问题：

      $\underset{x}{\mathrm{argmin}}\Vert X-B{\Vert }_2^2/2+\lambda \Vert X{\Vert }_1$

  这里用的对比函数是基追踪降噪 (BPDN_quadprog.m)，参见 压缩感知重构算法之基追踪降噪，使用 BPDN 时，实际上就是观测矩阵为单位阵时的一种特殊情况：

clear all;close all;clc; 
b = [-0.8487   -0.3349    0.5528    1.0391   -1.1176]';
lambda = 1;
x1=soft(b,lambda)
x2=BPDN_quadprog(b,eye(length(b)),lambda)
fprintf('\nError between soft and BPDN = %f\n',norm(x1-x2))

  这里就不给出输出结果了。运行后，观察输出结果可知，soft函数与BPDN_quadprog函数的输结果相同。

  另外，可以在matlab里输入以下命令看一个软阈值的图像：

x=-5:0.1:5;T=1;y=soft(x,T);plot(x,y);grid;