1 定义
1.1 硬阈值
硬阈值的定义如下:
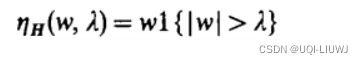
相当于

1.2 软阈值
软阈值的定义如下:

相当于

1.3 二者对比(可视化解释)
这是一张很经典地表述软阈值和硬阈值区别的图,其中软阈值是蓝色的线,他没有突变;硬阈值是红色的虚线,在±a的时候会有一个突变

2 二者的作用
2.1 硬阈值
硬阈值可以解决如下优化问题:
其中
表示是向量X的零范数(向量X中非零元素的个数)
根据范数的定义,我们可以把上面的优化问题逐项拆开:
这里
表示当前元素x是否非零
于是我们就可以将求解上述的一个优化问题转化为求解N个独立的优化问题
进一步,我们可以写成:
对于x≠0的部分,我们知道f(x)的最小值在x=b的时候取得,最小值为λ。
对于x=0的部分,我们就看
和λ哪个更小,小的将成为f(x)的最小值
如果
,那么最小值在x=b的时候取到;反之,那么最小值在x=0处取到,
也即
所以我们不难发现,这样的一个优化函数和硬阈值一一对应

2.2 软阈值
和硬阈值同理,软阈值也和一种形式的优化问题一一对应,唯一的区别是||X||在硬阈值中是零范数,在软阈值中是一范数
同样也可以把优化问题拆分开来
同样也可以解N个独立的优化函数
对f(x)求导,有:
零倒数为零,有:
(1) x小于0的时候,最小值在x取
的时候取到
如果
小于0(即
),那么的确argmin f(x)=
如果
大于0(即
),那么此时argmin f(x)=0
(2)x大于0的时候,最小值在x取
的时候取到
如果
大于0(即
),那么的确argmin f(x)=
如果
小于0(即
),那么此时argmin f(x)=0
总结一下,有:

参考资料












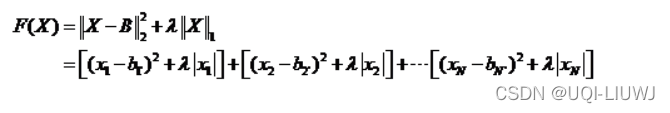



















 1138
1138

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










