文章目录
- 序言
- TODO : 每个框架10个题默写3遍
- 练习题
- labuldong 的刷题笔记目录
- 第⼀章、基础数据结构
- 第⼆章、进阶数据结构
- ⼆叉树
- 94. ⼆叉树的中序遍历
- 100. 相同的树
- 102. ⼆叉树的层序遍历
- 103. ⼆叉树的锯⻮形层序遍历
- 104. ⼆叉树的最⼤深度
- 144. ⼆叉树的前序遍历
- 543. ⼆叉树的直径
- 105. 从前序与中序遍历序列构造⼆叉树
- 106. 从中序与后序遍历序列构造⼆叉树
- 654. 最⼤⼆叉树
- 107. ⼆叉树的层序遍历 II
- 111. ⼆叉树的最⼩深度
- 114. ⼆叉树展开为链表
- 116. 填充每个节点的下⼀个右侧节点指针
- 226. 翻转⼆叉树
- 145. ⼆叉树的后序遍历
- 222. 完全⼆叉树的节点个数
- 236. ⼆叉树的最近公共祖先
- 297. ⼆叉树的序列化与反序列化
- 341. 扁平化嵌套列表迭代器
- 501. ⼆叉搜索树中的众数
- 559. N 叉树的最⼤深度
- 589. N 叉树的前序遍历
- 590. N 叉树的后序遍历
- 652. 寻找重复的⼦树
- 965. 单值⼆叉树
- ⼆叉搜索树
- 图论算法
- 第三章、暴⼒搜索算法
- 第四章、动态规划算法
- 第五章、其他经典算法
序言
解答以下的几个困惑:
- 不知道整么想
- 不知道整么做
- 不知道要注意些什么
稍微整理了一下,发现要搞懂的题目特别多,就收缩边界,不要展开,刷完leedcode前300道题,剩下的听天由命。
像 背单词⼀样背算法,对于各种算法技巧,如果没事⼉就看,哪有记不住的道理。
如果看了题 ⽬不能迅速想到解题思路,或者看了思路写不出代码,那就说明这块知识点掌握的不太好,需要重新复习巩固。
TODO : 每个框架10个题默写3遍
背包问题
排序
堆排序
//先写出一个节点的堆化操作,再遍历每个节点实现堆化,输出的话就是用最后一个节点替换第一个节点,再堆化。这需要一个过程
func SortArray() []int {
arr := []int{6, 3, 5, 4, 1, 2, 7}
build(arr)
var res []int
for len(arr) != 0 {
res = append(res, arr[0])
arr[0] = arr[len(arr)-1]
arr = arr[:len(arr)-1]
build(arr)
}
fmt.Println(res)
return res
}
func build(arr []int) {
for i := len(arr) - 1; i >= 0; i-- {
heapfy(arr, i)
}
}
func heapfy(nums []int, index int) {
if index == len(nums) || (2*index+1) >= len(nums) {
return
}
if (2*index + 2) >= len(nums) {
if nums[2*index+1] < nums[index] {
swap(nums, 2*index+1, index)
}
return
}
root := index
left := 2*index + 1
right := 2*index + 2
rootV := nums[root]
leftV := nums[left]
rightV := nums[right]
minV := rootV
if leftV < minV {
minV = leftV
swap(nums, left, root)
if left < len(nums) {
heapfy(nums, left)
}
}
if rightV < minV {
minV = rightV
swap(nums, right, root)
if right < len(nums) {
heapfy(nums, right)
}
}
return
}
func swap(nums []int, x, y int) {
temp := nums[x]
nums[x] = nums[y]
nums[y] = temp
}
堆排序:
力扣上能过
func sortArray(nums []int) []int {
// 堆排序-大根堆,升序排序,基于比较交换的不稳定算法,时间O(nlogn),空间O(1)-迭代建堆
// 遍历元素时间O(n),堆化时间O(logn),开始建堆次数多些,后面次数少
// 主要思路:
// 1.建堆,从非叶子节点开始依次堆化,注意逆序,从下往上堆化
// 建堆流程:父节点与子节点比较,子节点大则交换父子节点,父节点索引更新为子节点,循环操作
// 2.尾部遍历操作,弹出元素,再次堆化
// 弹出元素排序流程:从最后节点开始,交换头尾元素,由于弹出,end--,再次对剩余数组元素建堆,循环操作
// 建堆函数,堆化
var heapify func(nums []int, root, end int)
heapify = func(nums []int, root, end int) {
// 大顶堆堆化,堆顶值小一直下沉
for {
// 左孩子节点索引
child := root*2 + 1
// 越界跳出
if child > end {
return
}
// 比较左右孩子,取大值,否则child不用++
if child < end && nums[child] <= nums[child+1] {
child++
}
// 如果父节点已经大于左右孩子大值,已堆化
if nums[root] > nums[child] {
return
}
// 孩子节点大值上冒
nums[root], nums[child] = nums[child], nums[root]
// 更新父节点到子节点,继续往下比较,不断下沉
root = child
}
}
end := len(nums)-1
// 从最后一个非叶子节点开始堆化
for i:=end/2;i>=0;i-- {
heapify(nums, i, end)
}
// 依次弹出元素,然后再堆化,相当于依次把最大值放入尾部
for i:=end;i>=0;i-- {
nums[0], nums[i] = nums[i], nums[0]
end--
heapify(nums, 0, end)
}
return nums
}
力扣上超时了
package sort
import "fmt"
//堆排序
func main() {
arr := []int{1, 9, 10, 30, 2, 5, 45, 8, 63, 234, 12}
fmt.Println(HeapSort(arr))
}
func HeapSortMax(arr []int, length int) []int {
// length := len(arr)
if length <= 1 {
return arr
}
depth := length/2 - 1 //二叉树深度
for i := depth; i >= 0; i-- {
topmax := i //假定最大的位置就在i的位置
leftchild := 2*i + 1
rightchild := 2*i + 2
if leftchild <= length-1 && arr[leftchild] > arr[topmax] { //防止越过界限
topmax = leftchild
}
if rightchild <= length-1 && arr[rightchild] > arr[topmax] { //防止越过界限
topmax = rightchild
}
if topmax != i {
arr[i], arr[topmax] = arr[topmax], arr[i]
}
}
return arr
}
func HeapSort(arr []int) []int {
length := len(arr)
for i := 0; i < length; i++ {
lastlen := length - i
HeapSortMax(arr, lastlen)
if i < length {
arr[0], arr[lastlen-1] = arr[lastlen-1], arr[0]
}
}
return arr
}
多线程
- 实现1到100的累加求和
public static void main(String[] args) throws Exception {
AtomicInteger count = new AtomicInteger();
for (int i = 1; i <= 10; i++) {
int finalI = i;
Thread thread = new Thread(() -> {
for (int j = (finalI - 1) * 10 + 1; j <= finalI * 10; j++) {
count.addAndGet(j);
}
});
thread.start();
thread.join();
//join必须在start后⾯;join将两个交替执⾏的线程强制为按顺序执⾏。可以说将并⾏的改 成了串⾏}
//结果正确5050
}
System.out.println(count.get());
}
数据结构设计(LRU.LFU要求熟练背诵并默认)
LRU
LRU是从时间维度进行淘汰
// 错误设计1:list是拿不到当前节点的引用的
package main
import (
"container/list"
"fmt"
)
func main() {
obj := Constructor(2)
obj.Put(1, 1)
obj.Put(2, 2)
fmt.Println(obj.Get(1)) //2
obj.Put(3, 3)
fmt.Println(obj.Get(2)) //3
obj.Put(4, 4)
fmt.Println(obj.Get(1)) //4
fmt.Println(obj.Get(3)) //4
fmt.Println(obj.Get(4)) //4
}
type LRUCache struct {
capacity int
size int
cache map[int]*list.List
que *list.List
}
type node struct {
key, value int
}
func Constructor(capacity int) LRUCache {
return LRUCache{
capacity: capacity,
cache: make(map[int]*list.List),
que: list.New(),
}
}
func (this *LRUCache) Get(key int) int {
if v, ok := this.cache[key]; ok {
this.que.MoveBefore(v.Front(), this.que.Front())
return (v.Front().Value).(node).value
}
return -1
}
func (this *LRUCache) Put(key int, value int) {
if v, ok := this.cache[key]; ok {
this.que.MoveBefore(v.Front(), this.que.Front())
} else {
if this.size+1 > this.capacity {
//满了
this.que.Remove(this.que.Back())
delete(this.cache, key)
nd := node{
key: key,
value: value,
}
this.que.PushFront(nd)
this.cache[key] = this.que
} else {
nd := node{
key: key,
value: value,
}
this.que.PushFront(nd)
this.cache[key] = this.que
/**
我依次put了1,2,3
我希望的this.cache[key] = this.que是
1-2-3 实际 1-2-3
2-3 实际 1-2-3
3 实际 1-2-3
*/
this.size++
}
}
}
修正后的正确设计–基于golang的list.List双链表,它的remove是O(1),不像linkednode是O(n)
type LRUCache struct {
size int
capacity int
que *list.List
cache map[int]*list.Element
}
type Node struct {
key int
value int
}
func Constructor(capacity int) LRUCache {
cache := LRUCache{
size: 0,
capacity: capacity,
cache: make(map[int]*list.Element),
que: list.New(),
}
return cache
}
func (this *LRUCache) Get(key int) int {
if v, ok := this.cache[key]; ok {
/**
this.que.Remove(v)
node := v.Value.(Node)
push进去的是Node,那么下文取出来时Value.(*Node)就会报错,必须推进去是list.Element
this.que.PushFront(node)
*/
this.que.MoveToFront(v)
return v.Value.(*Node).value
}
return -1
}
func (this *LRUCache) Put(key int, value int) {
if v, ok := this.cache[key]; ok {
v.Value.(*Node).value = value
this.que.MoveToFront(v)
} else {
if this.size == this.capacity {
//满了
back := this.que.Back()
delete(this.cache, back.Value.(*Node).key)
this.que.Remove(back)
this.size--
}
front := this.que.PushFront(&Node{
key: key,
value: value,
})
this.cache[key] = front
this.size++
}
}
不符合时间复杂度的设计-java lineknode
// 不符合时间复杂度的设计2:lineknode的remove在改场景该用法的使用下时间复杂度是O(n)
class LRUCache {
private int capacity;
private Map<Integer, Integer> cache;
private LinkedList<Integer> link;
public LRUCache(int capacity) {
this.capacity = capacity;
cache = new HashMap<>();
link = new LinkedList<>();
}
public int get(int key) {
if (!cache.containsKey(key)) return -1;
else {
int value = cache.get(key);
link.remove(Integer.valueOf(key));
link.addFirst(key);
return value;
}
}
public void put(int key, int value) {
if (capacity == 0) return;
if (cache.containsKey(key)) { //k存在,更新缓存kv
cache.put(key, value);
link.remove(Integer.valueOf(key));
link.addFirst(key);
} else {
if (link.size() == capacity) {
cache.remove(Integer.valueOf(link.pollLast()));
}
link.addFirst(key);
cache.put(key, value);
}
}
}
自定义双链表的正确的LRU实现
type LRUCache struct {
size int
capacity int
cache map[int]*DLinkedNode
//双链表的经典实现,记录头节点和尾节点,并且头节点和尾节点都是虚拟哑结点(能极大简化链表的操作)
//双链表用空间换时间,可实现删除是O(1)
head, tail *DLinkedNode
}
type DLinkedNode struct {
key int
value int
prev, next *DLinkedNode
}
func initDLinkedNode(key, value int) *DLinkedNode {
return &DLinkedNode{
key: key,
value: value,
}
}
func Constructor(capacity int) LRUCache {
cache := LRUCache{
size: 0,
capacity: capacity,
cache: make(map[int]*DLinkedNode),
// 双链表的构造非常巧妙,初始化首尾2个哑结点
head: initDLinkedNode(0, 0),
tail: initDLinkedNode(0, 0),
}
cache.head.next = cache.tail
cache.tail.prev = cache.head
return cache
}
func (this *LRUCache) Get(key int) int {
if v, ok := this.cache[key]; ok {
val := v.value
this.moveToHead(v)
return val
}
return -1
}
func (this *LRUCache) Put(key int, value int) {
if v, ok := this.cache[key]; ok {
//this.moveToHead(v) //假设已有3,1,现在用户更新成了3,5,所以这个不能省v.value = value
v.value = value
this.moveToHead(v)
} else {
if this.size == this.capacity {
//满了
tail := this.removeTail()
//删除的是key,不是value,不要写成tail.value,这里非常容易不动脑子的写成value
delete(this.cache, tail.key)
this.size--
}
node := initDLinkedNode(key, value)
this.addToHead(node)
this.cache[key] = node
this.size++
}
}
func (this *LRUCache) addToHead(node *DLinkedNode) {
/**
this.head.next = node
node.prev = this.head
this.head.next.prev = node
//this.tail.prev = node //写错了,正确写法见上
node.next = this.head.next
//node.next = this.tail //写错了,正确写法见上
*/
node.prev = this.head
node.next = this.head.next
this.head.next.prev = node
this.head.next = node
}
func (this *LRUCache) removeNode(node *DLinkedNode) {
/**错误写法
p := node.prev
n := node.next
n.next = p
p.next = n
*/
node.prev.next = node.next
node.next.prev = node.prev
}
func (this *LRUCache) moveToHead(node *DLinkedNode) {
//先移除节点,在添加到头部,非常妙,简化了移动指针的很复杂的操作
this.removeNode(node)
this.addToHead(node)
}
func (this *LRUCache) removeTail() *DLinkedNode {
prev := this.tail.prev
this.removeNode(prev)
return prev
}
LFU
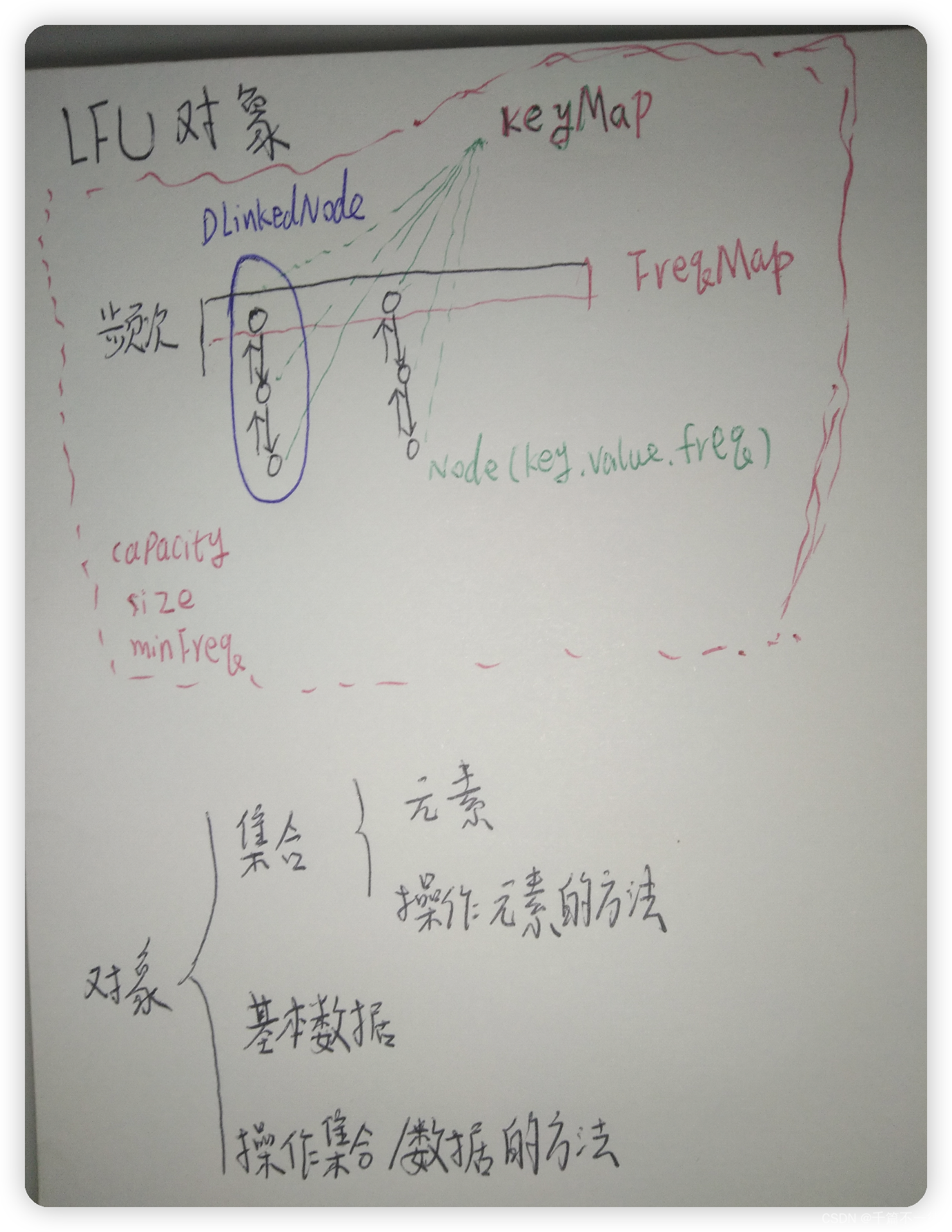
LFU根据使用频次进行淘汰-同频再根据时间淘汰
type LFUCache struct {
minFreq int
size int
capacity int
freqTable map[int]*DLinkedNode
keyTable map[int]*Node
}
func Constructor(capacity int) LFUCache {
cache := LFUCache{
size: 0,
capacity: capacity,
freqTable: make(map[int]*DLinkedNode),
keyTable: make(map[int]*Node),
minFreq: 0,
}
return cache
}
func (this *LFUCache) Get(key int) int {
if val, ok := this.keyTable[key]; ok {
value := val.value
freq := val.freq
lnode := this.freqTable[freq]
lnode.remove(val)
delete(this.keyTable,key)
aa := this.freqTable[this.minFreq]
if aa.head.next == aa.tail {
this.minFreq++
}
if mv, ok := this.freqTable[freq+1]; ok {
n :=initNode(key, value, freq+1)
mv.addFirst(n)
this.keyTable[key]=n
} else {
lnode := initDLinkedNode()
node := initNode(key, value, freq+1)
this.keyTable[key] = node
lnode.addFirst(node)
this.freqTable[freq+1] = lnode
}
return value
} else {
return -1
}
}
func (this *LFUCache) Put(key int, value int) {
if val, ok := this.keyTable[key]; ok {
//升级频率
freq := val.freq
lnode := this.freqTable[freq]
lnode.remove(val)
aa := this.freqTable[this.minFreq]
if aa.head.next == aa.tail {
this.minFreq++
}
if mv, ok := this.freqTable[freq+1]; ok {
n := initNode(key, value, freq+1)
mv.addFirst(n)
this.keyTable[key] = n
} else {
lnode := initDLinkedNode()
node := initNode(key, value, freq+1)
this.keyTable[key] = node
lnode.addFirst(node)
this.freqTable[freq+1] = lnode
}
} else {
if this.size == this.capacity {
if this.capacity == 0 {
return
} else {
prev := this.freqTable[this.minFreq].tail.prev
this.freqTable[this.minFreq].remove(prev)
delete(this.keyTable, prev.key)
//delete(this.freqTable, this.minFreq) capity容量表示能放多少个key,而不是频次分类的key数量
this.size--
}
}
if val, ok := this.freqTable[1]; ok {
n := initNode(key, value, 1)
val.addFirst(n)
this.keyTable[key] = n
} else {
lnode := initDLinkedNode()
node := initNode(key, value, 1)
this.keyTable[key] = node
lnode.addFirst(node)
this.freqTable[1] = lnode
}
this.size++
this.minFreq = 1
}
}
type Node struct {
key int
value int
freq int
prev, next *Node
}
type DLinkedNode struct {
head, tail *Node
}
func (n DLinkedNode) addFirst(node *Node) {
node.next = n.head.next
n.head.next.prev = node
n.head.next = node
node.prev = n.head
}
func (n DLinkedNode) remove(val *Node) {
nt := val.next
p := val.prev
p.next = nt
nt.prev = p
}
func initDLinkedNode() *DLinkedNode {
head := initNode(0, 0, 0)
tail := initNode(0, 0, 0)
head.next = tail
tail.prev = head
return &DLinkedNode{
head: head,
tail: tail,
}
}
func initNode(key, value, freq int) *Node {
return &Node{
key: key,
value: value,
freq: freq,
}
}





















 3859
3859











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








