什么是一阶梯度下降法
- 这里主要说一下所谓的一阶是什么意思,至于梯度下降法,我觉得点进来的同学们应该都知道它是什么,以及用处。如果不清楚,下面还会讲解。
- 这里所谓的一阶就是指仅考虑一阶导数的梯度下降法(或者说只考虑梯度的梯度下降法,而没考虑曲率,即二阶导数)
推导过程
- 用泰勒公式来推导一阶梯度下降法的公式。首先带大家熟悉回顾一下泰勒公式:
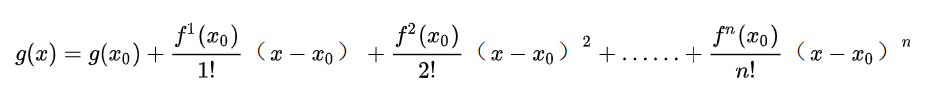
- 然后看一下我们的目标函数,以梯度下降法在深度学习中的应用为例,设 L ( θ ) L(θ) L(θ)是损失函数,我们希望随着参数 θ θ θ的调整,损失函数的值 L ( θ ) L(θ) L(θ)是逐渐下降的。泰勒公式是用来拟合逼近曲线的,这与损失函数有什么关系呢?别急听我慢慢道来。
- 在 x 0 x_0 x0处的泰勒展开式的含义是以 x 0 x_0 x0为起点来构造函数,使其逐渐与目标函数相似,而开的阶数越多,函数就越相似。具体有关泰勒公式的我不展开描述了,有需要补充知识的点击:https://www.zhihu.com/question/25627482。其实在我们这里并没有明显的曲线的意义,我们只有一个对应某个输入 x x x,使用参数 θ θ θ计算而来的损失函数而已。但是这里有隐含的“曲线”,一般的曲线,以横坐标x为自变量,然后因变量y随之改变。而我们这里每次输入的数据基本都是一致的(神经网络每批次的输入数据分布是基本一致的),而我们要让损失函数 L ( θ ) L(θ) L(θ)不断降低,这本身不就是一个曲线嘛?只不过是“原地踏步”的曲线,每次输入相似的 x x x,通过更改参数使得 y y y(即 L ( θ ) L(θ) L(θ))不断降低。所以说,对于每一次的损失函数值,我们可以用泰勒函数来逼近。如果还是没太听明白,别着急,下面继续。
- 我们设第k次的参数为 θ k θ_k θk,现进行第k+1次训练, L ( θ k ′ ) L(θ'_{k}) L(θk′)是根据本次训练输入的数据得到的理想情况下的最低损失,其中 θ k ′ θ'_{k} θk′是对应该输入数据的最优参数。而我们实际的参数是 θ k θ_k θk,显然不是最优的,所以使用实际参数得到的损失 L ( θ k ) L(θ_k) L(θk)是大于最优损失 L ( θ k ′ ) L(θ'_{k}) L(θk′)的,因此我们要对参数进行调整,也可以说是对曲线进行拟合,所以用到了泰勒公式。
- 下面对最优参数下的损失进行一阶泰勒公式展开:
L ( θ k ′ ) = L ( θ k ) + L ′ ( θ k ) ( θ k ′ − θ k ) L(θ'_{k})=L(θ_{k})+L'(θ_{k})(θ'_{k}-θ_{k}) L(θk′)=L(θk)+L′(θk)(θk′−θk),其中 L ′ ( θ k ) L'(θ_{k}) L′(θk)是一阶导数。我们要调整 θ k θ_{k} θk从而使上式右式尽可能逼近左式。我们知道, θ k θ_{k} θk和 θ k ′ θ'_{k} θk′都是高维向量,而两个高维向量差的不过是大小和方向两点。知道了这一点,我们就可以对上式的 ( θ k ′ − θ k ) (θ'_{k}-θ_{k}) (θk′−θk)进行改造:
设 ( θ k ′ − θ k ) = η v (θ'_{k}-θ_{k})=ηv (θk′−θk)=ηv,其中η含义=(步长,变化大小,标量),v含义=(变化方向,单位向量)。
所以得到:
L ( θ k ′ ) = L ( θ k ) + η v L ′ ( θ k ) L(θ'_{k})=L(θ_{k})+ηvL'(θ_{k}) L(θk′)=L(θk)+ηvL′(θk)
又因为 L ( θ k ′ ) < L ( θ k ) L(θ'_{k})<L(θ_{k}) L(θk′)<L(θk),所以
L ( θ k ′ ) − L ( θ k ) = η v L ′ ( θ k ) < 0 L(θ'_{k})-L(θ_{k})=ηvL'(θ_{k})<0 L(θk′)−L(θk)=ηvL′(θk)<0
也就是说,如果想要参数调整之后损失变小,那么就要满足上式,而v是一个单位向量,函数的导数也是一个向量(函数增长方向),那么两个向量的乘积在什么时候小于0呢?
根据向量乘积公式:
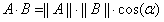
当cos(α)<0,时向量乘积小于0 ,因为我们希望下降速度是最快的,所以令cos(α) = -1,即两个向量的方向相反。那么知道了 v v v与 L ′ ( θ k ) L'(θ_{k}) L′(θk)方向相反,且是个单位向量,所以 v v v为:
v = − L ′ ( θ k ) / ∣ ∣ L ′ ( θ k ) ∣ ∣ v=-L'(θ_{k})/||L'(θ_{k})|| v=−L′(θk)/∣∣L′(θk)∣∣
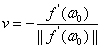
所以 ( θ k ′ − θ k ) = − η L ′ ( θ k ) / ∣ ∣ L ′ ( θ k ) ∣ ∣ (θ'_{k}-θ_{k})=-ηL'(θ_{k})/||L'(θ_{k})|| (θk′−θk)=−ηL′(θk)/∣∣L′(θk)∣∣,又因为 η η η和 ∣ ∣ L ′ ( θ k ) ∣ ∣ ||L'(θ_{k})|| ∣∣L′(θk)∣∣是标量,所以用一个字母代替即为:
θ k ′ = θ k − η L ′ ( θ k ) θ'_{k}=θ_{k}-ηL'(θ_{k}) θk′=θk−ηL′(θk)
后来人们赋予了这个标量新的意义,即学习率 r r r,人们认为, L ′ ( θ k ) L'(θ_{k}) L′(θk)提供了参数更改的力度和方向,而学习率 r r r用于调整这个力度。 - 还没完,有个同学问过我,为什么需要学习率,看上去学习率好像限制了学习的量,既然知道了调整的方向和力度,为什么不一次性调到对应本批次数据最合适的参数呢?其实问题出在泰勒公式上,泰勒公式随着求导的阶数提升而更加精准,而我们只是进行了一阶求导,换句话说,你这个 L ′ ( θ k ) L'(θ_{k}) L′(θk)方向也不一定是最好的方向,力度(即梯度)自然也是不一定最优了。而我们每次迭代只前进一小步,不求一次中的,但求更加逼近。同时你也要知道,你学习率越大,意味着走的步长越大,这样的话误差是越大的,不明白的话就是泰勒公式不熟悉,看看这个就明白了:https://www.zhihu.com/question/25627482
弊端
- 一阶求导看上去似乎没有什么太大的毛病,但是学习率的控制是一个大的弊端,它会导致出现zigzag型下降。
- 一阶求导可以做到的事情实在是有限,它都无法判断凹凸性,而倘若知道二阶导数的话,是可以求解凹凸性的,它可以知道函数的曲率,那知道凹凸性、曲率有什么好处呢,答案是它可以指导本次修改参数所使用的学习率大小。曲率大的地方意味着导数的变化率是非常大的,在这里要“慢点走”,即学习率小一点,而对于导数变化率不大的地方,则需要快点走。所以说一阶求导的收敛速度还有改进的空间。
改进
- 可以参考收敛速度更快的牛顿法。

























 6766
6766











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










