ML-逻辑回归

ML-逻辑回归

参考视频：https://www.bilibili.com/video/BV1Rt411q7WJ

一、逻辑回归

逻辑回归解决的问题是分类问题。

Sigmoid/Logistic Function

我们定义逻辑回归的预测函数为$h_{\theta }(x)=g({\theta }^{T}x)$，其中$g(x)$函数是$sigmoid$函数。

$sigmoid$函数图像

0.5可以作为分类的边界：
当$z\ge 0$的时候$g(z)\ge 0.5$，当${\theta }^{T}X\ge 0$的时候$g({\theta }^{T}X)\ge 0.5$；
当$z\le 0$的时候$g(z)\le 0.5$，当${\theta }^{T}X\le 0$的时候$g({\theta }^{T}X)\le 0.5$。

决策边界

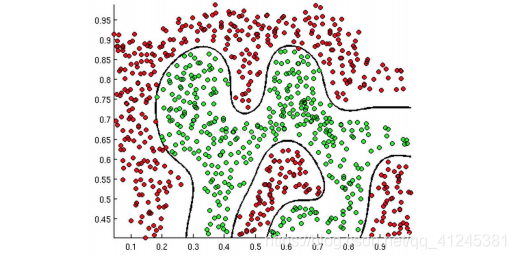
代价函数

当$y=1$，$h_{\theta }(x)=1$时，$cost=0$
当$y=1$，$h_{\theta }(x)=0$时， c o s t = ∞ cost=∞ cost=∞</