前言
在机器学习算法中,对于很多监督学习模型,需要对原始的模型构建损失函数,接下来便是通过优化算法对损失函数进行优化,以便寻找到最优的参数。在求解机器学习参数的优化算法中,使用较多的是基于梯度下降的优化算法(Gradient Descent, GD)。
梯度下降法有很多优点,其中,在梯度下降法的求解过程中,只需求解损失函数的一阶导数,计算的代价比较小,这使得梯度下降法能在很多大规模数据集上得到应用。梯度下降法的含义是通过当前点的梯度方向寻找到新的迭代点。
基本思想可以这样理解:我们从山上的某一点出发,找一个最陡的坡走一步(也就是找梯度方向),到达一个点之后,再找最陡的坡,再走一步,直到我们不断的这么走,走到最“低”点(最小花费函数收敛点)。
目的
总结一句话就是梯度下降算法是通过最小化损失函数,达到最优化拟合模型参数的目的。
【优化参数的另一种方法:最小二乘法】https://blog.csdn.net/qq_36330643/article/details/78391645
实例讲解
单变量函数的梯度下降
我们假设有一个单变量的函数
求导
初始化,起点为
设定学习率为
根据梯度下降的计算公式
我们开始进行梯度下降的迭代计算过程:
如图,经过四次的运算,也就是走了四步,基本就抵达了函数的最低点,也就是山底
判断达到山地的依据:的变化量很小了接近于零,在真正算法实现中需要自己设定这个参数
多变量函数的梯度下降
我们假设有一个目标函数
现在要通过梯度下降法计算这个函数的最小值。我们通过观察就能发现最小值其实就是 (0,0)点。但是接下来,我们会从梯度下降算法开始一步步计算到这个最小值!
我们假设初始的起点为:
初始的学习率为:
函数的梯度为:
进行多次迭代:
我们发现,已经基本靠近函数的最小值点
关于参数
1、学习率
也叫步长,如果学习率过大可能会出现无法收敛的情况;过小会出现迭代很多次才会得到最优解的情况,效率太低。
所以在实际操作的时候,要根据实际情况进行步长的调整。
调整方法:【参考https://www.zhihu.com/question/37911687】

最后,我最近有篇paper关于这个问题,等发了再说→_→
参考文献:
[1] Nocedal, Jorge, and Stephen Wright. Numerical optimization. Springer Science & Business Media, 2006.
[2] Fletcher, R. (2005). On the barzilai-borwein method. In Optimization and control with applications (pp. 235-256). Springer US.
[3] Raydan, Marcos. "On the Barzilai and Borwein choice of steplength for the gradient method." IMA Journal of Numerical Analysis 13.3 (1993): 321-326.
[4] Roux, Nicolas L., Mark Schmidt, and Francis R. Bach. "A stochastic gradient method with an exponential convergence _rate for finite training sets." Advances in Neural Information Processing Systems. 2012.
[5] Mahsereci, Maren, and Philipp Hennig. "Probabilistic line searches for stochastic optimization." Advances In Neural Information Processing Systems. 2015.
[6] Massé, Pierre-Yves, and Yann Ollivier. "Speed learning on the fly." arXiv preprint arXiv:1511.02540 (2015).
2、阈值
怎么衡量是否已经找到了最优解,这时就要这时就要设定阈值,当参数的变化量小于这个阈值时就退出迭代,表明已经非常接近最优解了,注意这里是接近,不是说就是找到了真正的最优解。
局部最优VS全局最优

在不考虑模型过拟合的情况下,梯度下降得到的最优解不一定是全局最优解,也有可能是局部最优解
在下降过程中,我们找到了一个数据无变化的点(不动点),这个不动点可能有三个含义:极大值、极小值和鞍点。在梯度下降中,极大值基本上可能性没有,只有可能是极小值和鞍点。当前仅当梯度下降是凸函数时,梯度下降会收敛到最小值。
也就是在使用梯度下降中,我们最大可能得到是局部最优解。
为了确保不动点是局部最优解,可以设置更小的退出阈值,进行多次比较看看参数是否变化,如果变化了,说明可以再次调试。
解决回归问题
下面我们将用python实现一个简单的梯度下降算法。场景是一个简单的线性回归的例子:假设现在我们有一系列的点,如下图所示
我们将用梯度下降法来拟合出这条直线!
首先,我们需要定义一个代价函数,在此我们选用均方误差代价函数
此公式中
- m是数据集中点的个数
- ½是一个常量,这样是为了在求梯度的时候,二次方乘下来就和这里的½抵消了,自然就没有多余的常数系数,方便后续的计算,同时对结果不会有影响
- y 是数据集中每个点的真实y坐标的值
-
h 是我们的预测函数,根据每一个输入x,根据Θ 计算得到预测的y值,即
-
我们可以根据代价函数看到,代价函数中的变量有两个,所以是一个多变量的梯度下降问题,求解出代价函数的梯度,也就是分别对两个变量进行微分
明确了代价函数和梯度,以及预测的函数形式。我们就可以开始编写代码了。但在这之前,需要说明一点,就是为了方便代码的编写,我们会将所有的公式都转换为矩阵的形式,python中计算矩阵是非常方便的,同时代码也会变得非常的简洁。
为了转换为矩阵的计算,我们观察到预测函数的形式
我们有两个变量,为了对这个公式进行矩阵化,我们可以给每一个点x增加一维,这一维的值固定为1,这一维将会乘到Θ0上。这样就方便我们统一矩阵化的计算
然后我们将代价函数和梯度转化为矩阵向量相乘的形式
code:
import numpy as np
import matplotlib.pyplot as plt
# Size of the points dataset.
m = 20
#定义数据集和学习率
# Points x-coordinate and dummy value (x0, x1).
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))
# Points y-coordinate
y = np.array([
3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)
# The Learning Rate alpha.
alpha = 0.01
#接下来我们以矩阵向量的形式定义代价函数和代价函数的梯度
def error_function(theta, X, y):
'''Error function J definition.'''
diff = np.dot(X, theta) - y
return (1./2*m) * np.dot(np.transpose(diff), diff)
def gradient_function(theta, X, y):
'''Gradient of the function J definition.'''
diff = np.dot(X, theta) - y
return (1./m) * np.dot(np.transpose(X), diff)
#梯度下降迭代计算
def gradient_descent(X, y, alpha):
'''Perform gradient descent.'''
theta = np.array([1, 1]).reshape(2, 1)
gradient = gradient_function(theta, X, y)
#当梯度小于1e - 5
#时,说明已经进入了比较平滑的状态,类似于山谷的状态,这时候再继续迭代效果也不大了,
#所以这个时候可以退出循环!
while not np.all(np.absolute(gradient) <= 1e-5):
theta = theta - alpha * gradient
gradient = gradient_function(theta, X, y)
return theta
def draw():
x = np.linspace(0, 20, 500)
test_y = optimal[0] + x * optimal[1]
plt.figure()
plt.plot(x, test_y)
plt.scatter(X1, y, color='red')
plt.show()
optimal = gradient_descent(X, y, alpha)
print('optimal:', optimal)
print('error function:', error_function(optimal, X, y)[0,0])
draw()
运行代码,计算得到的结果如下
所拟合出的直线如下

梯度下降算法的优化
【参考博客https://blog.csdn.net/u012328159/article/details/80252012】
【参考博客https://www.cnblogs.com/kendrick/p/7678016.html】
在上面解决回归问题时,每次迭代使用所有的样本进行更新操作,称为BGD【批量梯度下降】,但是当面临样本非常大时,每迭代一次就会耗费大量时间,为了针对该问题进行优化提出了SGD【随机梯度下降】、MBGD【小批量梯度下降】
1. Batch gradient descent(BGD)
BGD 称为批量梯度下降,就是原始的梯度下降,每次迭代使用所有的样本进行更新操作。
BGD 的优点:
每次更新的梯度估计方向直接指向收敛的最小值点,最终达到收敛点
BGD 的缺点:
数据量庞大时,每一次迭代都需要耗费很大的时间
2. Stochastic gradient descent(SGD)
SGD 称为随机梯度下降,每次迭代使用的仅仅是随机的一个样本。
SGD 的优点:
因为只有一个样本,每次更新迭代速度快可以作为在线算法,不断使用新的数据更新参数
SGD 的缺点:
每次梯度估计方向都不确定,可能需要很长的时间接近最小值点,永远不会收敛
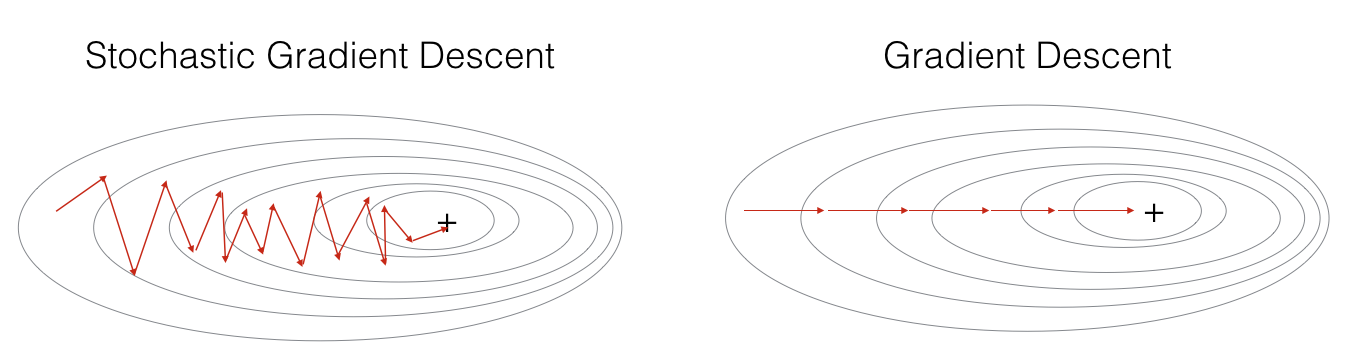
因为每次只用一个样本来更新参数,会导致不稳定性大些(可以看下图(图片来自ng deep learning 课),每次更新的方向,不想batch gradient descent那样每次都朝着最优点的方向逼近,会在最优点附近震荡)。因为每次训练的都是随机的一个样本,会导致导致梯度的方向不会像BGD那样朝着最优点。
注意:代码中的随机把数据打乱很重要,因为这个随机性相当于引入了“噪音”,正是因为这个噪音,使得SGD可能会避免陷入局部最优解中。
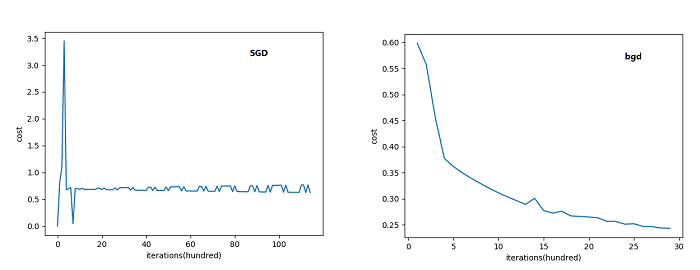
对比损失函数
可以看到SGD的代价函数随着迭代次数是震荡式的下降的(因为每次用一个样本,有可能方向是背离最优点的)
3. Mini-batch gradient descent(MBGD)
MBGD 称为小批量梯度下降,每次迭代使用一个以上又不是全部的样本。
MBGD 的优点:
使用多个样本相比 SGD 提高了梯度估计的精度
小批量的估计,相当于在学习过程中加入了噪声,会有一些正则化的效果,提高模型在测试集上的准确度
MBGD 的缺点:
同 SGD 一样,每次梯度估计的方向不确定,可能需要很长时间接近最小值点,不会收敛
通常在使用 MBGD 之前先将数据集随机打乱,然后再划分 Mini-batch,所以 MBGD 有时也称为 SGD 。
Mini-batch 大小的选择通常使用 2 的幂数,可以获得更少的运行时间。
遍历完所有数据,称为一个 epoch ,通常需要遍历几次 epoch 才行。
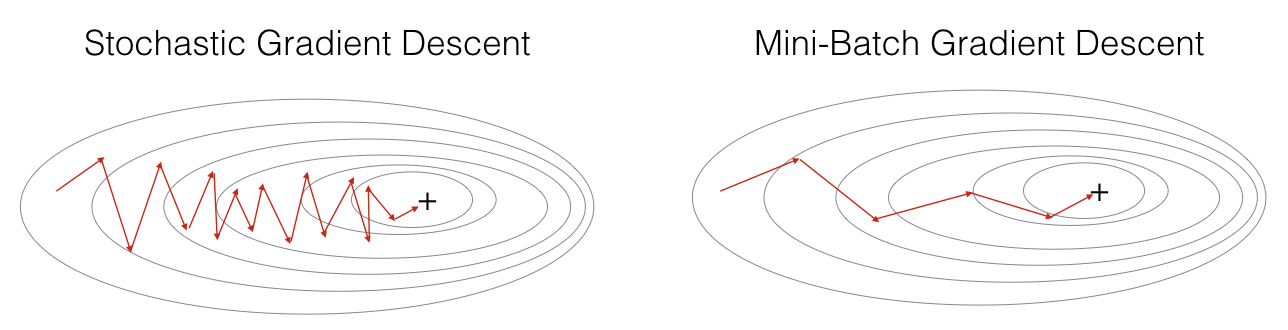
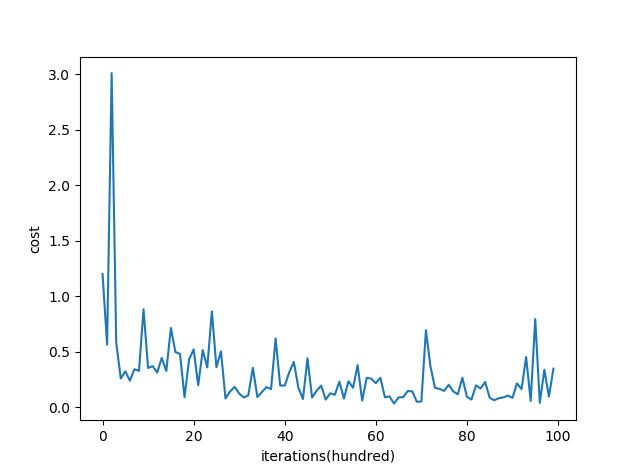
从图中能够看出,mini-batch gradient descent 相对SGD在下降的时候,相对平滑些(相对稳定),不像SGD那样震荡的比较厉害。mini-batch gradient descent的一个缺点是增加了一个超参数 batch_sizebatch_size ,要去调这个超参数。





















 2484
2484











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








