麻省理工公开课: 线性代数 第二讲 (矩阵消元)

一、矩阵消元（高斯消元法）

　　在解方程组时我们经常用到消元法，通过对方程的倍乘、加减等操作可以得到所求方程的解。

　　既然方程组可以用消元法进行求解，那么方程组变成矩阵自然也可以使用消元法。

　　矩阵消元目的主要是通过行变换将矩阵对角线下方的数字都变成0，从而可以回代求线性方程组的解

　　我们用该方程组演示： ，拿出它的系数矩阵A：，右侧向量b：

　　消元的过程是将A进行行变换得到上三角阵U，然后回代右侧向量，最后求解

　1.消元的知识准备：对左侧系数矩阵消元（A->U）

　　我们保留矩阵的第一行，然后消去下方所有行的多余变量

　　先从x位置开始。

　　既然要消去x，那么我们只需要关心矩阵的第一列，如图。

　　在图中我们可以看到，关键的位置是红色标记的1（我们将这种位置的数字称为“主元”，因为它是第一个出现的，所以叫它“主元一”），而我们的目的是将蓝色标记的位置都变成0。

　　操作很简单，第一行不变（因为它是主元行），第二行整体减去一倍的第一行，第三行不做变化（因为它本来就是0）。

　　于是我们得到了如下图的矩阵，可以看到，第一列的元素除了第一行都变成了0。

　　然后，我们处理y。

　　继续观察矩阵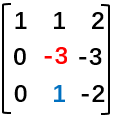        

　　如今，-3是新的主元（主元二），而我们要消去的是蓝色位置的1。

　　操作依旧简单，第一、二行都不变，将第三行减去-1/3倍的第二行。

　　然后得到这样的一个矩阵。（把主元标记一下）

　　事实上对系数矩阵的消元到这里就结束了，我们得到了一个上三角矩阵（因为它只有上半部分的三角形里有数字），我们用U表示它。

　　顺便一提，消元时主元不能为0，如果主元为0，可以将主元所在的行与它下面的主元位置非0的行进行交换（比如 变成）。

　　再顺便一提，行列式的值就是主元的乘积，所以该矩阵行列式得9

　　如果没有可以进行交换的行，方程无解，这种情况以后再讨论。

　2.消元的第一步：对增广矩阵消元（[A  b] -> [U  b']）

　　在正常的对方程组的消元过程中，等号右边的项与左边进行相同的操作，在矩阵中也是一样。

　　对于方程组，我们得到了它的系数矩阵A：，然后，我们把它的右侧向量b：放到A中，得到一个新矩阵：

　　我们管这个新矩阵叫做“增广矩阵”，因为它是原矩阵增加一部分构成的，我们可以把它写作[A  b]。

　　对于增广矩阵的每一行，我们作与上方系数矩阵消元相同的操作，从而得到U和经过行变换的b构成的增广矩阵[U  b']

　　注：正常的消元直接操作增广矩阵即可，上面对系数矩阵单独消元只是为了加深各位的理解。

　3.消元的第二步：回代

　　经过上面的变换，增广矩阵变成了这个样子：。

　　把它改写成方程组

　　求解，得到x=-1/9,y=-4/9,z=7/9

 

 二、用矩阵描述消元过程：E[A  b]=[U  b']

　　上方我们讨论了如何进行矩阵消元，现在，让我们换一种思考方式，用矩阵相乘来描述消元的过程。

　（1）预备知识

　　之前我们曾讨论过矩阵乘向量的问题，我们的结论是：矩阵乘向量的结果实际是矩阵列的线性组合。

　　但是，矩阵消元用到的都是矩阵的行，那么，矩阵的行之间是否也有相似的性质呢？按套路来讲，如果没有这种性质我就不会问这个问题了。

　　事实上，当一个向量乘一个矩阵时，得到的结果就是该矩阵行的线性组合。

　　比如，其结果相当于1*[1 1] + 2*[1 -2] = [3 -3]。

　　这里加上一些略微超前的概念：在一个矩阵A的左边乘一个矩阵（简称左乘），就是对A进行行变换，而在A右边乘一个矩阵（简称右乘），就是对A进行列变换。

　（2）用矩阵消元

　　我们依然用这个方程进行演示，拿出它的系数矩阵A：，右侧向量b:

　　我们想要得到一个矩阵E，它可以表示出我们消元的整个过程，也就是用E与A相乘便能直接得到U

　　还记得我们之前消元的步骤么？

　　1.首先，保持第一行不变，第二行整体减去一倍的第一行，第三行同样不变。

　　即，我们需要拿出-1倍的第一行，然后将它和第二行进行线性组合（相加），然后其他行不变（注意，在矩阵消元时我们是用两行相减，而“线性组合”是相加）。

　　按照需求，我们只需要在A的左边乘上（我们用E1表示这个矩阵）

　　为什么是这个矩阵？我们一行一行地看。

　　首先，A的第一行不变，因此我们需要拿出A的1个第一行，0个第二行，0个第三行（进行线性组合），于是1 0 0组成了E1的第一行。

　　然后，我们需要-1个A的第一行，1个第二行，0个第三行进行线性组合，所以 -1 1 0组成了E1的第二行。

　　第三行不变，因此需要0个第一行，0个第二行，1个第三行，所以E1的第三行是0 0 1

　　经过变换，我们得到了。

　　2.然后，保持一、二行不变，将1/3个第二行与第三行进行线性组合

　　可以自己写出需要左乘的矩阵吗？尝试着自己推导一下

　　你的结果是它吗 ？我们用E2来表示这个矩阵。

　　经过这次变换，我们得到了我们想要的矩阵U：(U是一个上三角矩阵）。

　　现在，我们可以用一个不太完美的式子来表达消元的全过程了：

　　E2(E1A)=U

　　3.最后，合并消元步骤

　　我们想要的结果是类似于EA=U这样的干净整洁的式子，怎么做到呢？

　　在这里需要引入一条新的有关矩阵乘法的性质：矩阵乘法满足结合律（但不满足交换律）

　　换句话说，E2(E1A)=(E2E1)A。（但AB≠BA）

　　即E=(E2E1)，我们管E叫做消元矩阵。

　　4.整体描述

　　用矩阵描述消元便是找到一个矩阵E（由每一步消元的消元矩阵相乘得到），使得EA=U，然后将其应用于增广矩阵[A  b]从而得到[U  b']，完成消元。

 

　　后面还会介绍EA=U的变形

三、置换矩阵

　　我们可以用矩阵相乘来完成矩阵的行交换与列交换，而用到的矩阵便叫做置换矩阵

　行交换

　　我们消元时通过左乘矩阵实现了行与行的线性组合，那么，如果想要将两行进行交换，需要怎么做呢？

　　召唤个矩阵先：

　　假设我们想要这个矩阵的第一二行（得到）

　　对于新矩阵的第一行，我们相当于拿出了0个原矩阵的第一行，1个原矩阵的第二行，0个原矩阵的第三行。

　　对于新矩阵的第二行，我们相当于拿出了1个原矩阵的第一行，0个原矩阵的第二行，0个原矩阵的第三行。

　　对于新矩阵的第三行，我们相当于拿出了0个原矩阵的第一行，0个原矩阵的第二行，1个原矩阵的第三行。

　　因此，我们只需在原矩阵的基础上左乘一个。（各行颜色不同是为了便于理解其构成方式，没有其他特别含义）

　　我们管左乘的这个矩阵叫做置换矩阵，用P表示。

　列交换

　　之前提到过，左乘即操作行，右乘即操作列

　　召唤一个矩阵：

　　想要交换这个矩阵的第一二列，得到

　　对于新矩阵的第一列，我们相当于拿出了0个原矩阵的第一列，1个原矩阵的第二列，0个原矩阵的第三列。

　　对于新矩阵的第二列，我们相当于拿出了1个原矩阵的第一列，0个原矩阵的第二列，0个原矩阵的第三列。

　　对于新矩阵的第三列，我们相当于拿出了0个原矩阵的第一列，0个原矩阵的第二列，1个原矩阵的第三列。

　　所以，只需要右乘

　　注意：这个矩阵虽然和上面交换行的置换矩阵长相相同，但性质与构成的方式却完全不同（行交换的置换矩阵是一行一行构成的，而列交换的却是一列一列构成的）

转载: https://www.cnblogs.com/Dumblidor/p/5751579.html

框神代码:

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <set>
#include <cstring>
#include <stack>
#include <set>
#include <vector>
#include <map>
#include <queue>
#define Swap(a,b)  a ^= b ^= a ^= b
#define pi acos(-1)
#define cl(a,b) memset(a,b,sizeof(a))
#define lson rt<<1
#define rson rt<<1|1
using namespace std ;
typedef long long LL;
//const int N = 1e7+10 ;
const int inf = 0x3f3f3f3f;
const int MAX = 100;
inline int gcd(int a,int b){return b?gcd(b,a%b):a;}
inline int lcm(int a,int b){return a/gcd(a,b)*b;}
const int MAXN=50;
int a[MAXN][MAXN];//增广矩阵
int x[MAXN];//解集
bool free_x[MAXN];//标记是否是不确定的变元
    // 高斯消元法解方程组(Gauss-Jordan elimination).(-2表示有浮点数解，但无整数解，
    //-1表示无解，0表示唯一解，大于0表示无穷解，并返回自由变元的个数)
    //有equ个方程，var个变元。增广矩阵行数为equ,分别为0到equ-1,列数为var+1,分别为0到var.
int Gauss(int equ,int var){
    int i,j,k;
    int max_r;// 当前这列绝对值最大的行.
    int col;//当前处理的列
    int ta,tb;
    int LCM;
    int temp;
    int free_x_num;
    int free_index;

    for(int i=0;i<=var;i++){
        x[i]=0;
        free_x[i]=true;
    }
    //转换为阶梯阵.
    col=0; // 当前处理的列
    for(k = 0;k < equ && col < var;k++,col++){// 枚举当前处理的行.
    // 找到该col列元素绝对值最大的那行与第k行交换.(为了在除法时减小误差)
        max_r=k;
        for(i=k+1;i<equ;i++){
            if(abs(a[i][col])>abs(a[max_r][col])) max_r=i;
        }
        if(max_r!=k){// 与第k行交换.
            for(j=k;j<var+1;j++) swap(a[k][j],a[max_r][j]);
        }
        if(a[k][col]==0){// 说明该col列第k行以下全是0了，则处理当前行的下一列.
            k--;
            continue;
        }
        for(i=k+1;i<equ;i++){// 枚举要删去的行.
            if(a[i][col]!=0){
                LCM = lcm(abs(a[i][col]),abs(a[k][col]));
                ta = LCM/abs(a[i][col]);
                tb = LCM/abs(a[k][col]);
                if(a[i][col]*a[k][col]<0)tb=-tb;//异号的情况是相加
                for(j=col;j<var+1;j++){
                    a[i][j] = a[i][j]*ta-a[k][j]*tb;
                }
            }
        }
    }
    // 1. 无解的情况: 化简的增广阵中存在(0, 0, ..., a)这样的行(a != 0).
    for (i = k; i < equ; i++){ // 对于无穷解来说，如果要判断哪些是自由变元，那么初等行变换中的交换就会影响，则要记录交换.
        if (a[i][col] != 0) return -1;
    }
    // 2. 无穷解的情况: 在var * (var + 1)的增广阵中出现(0, 0, ..., 0)这样的行，即说明没有形成严格的上三角阵.
    // 且出现的行数即为自由变元的个数.
    if (k < var){
        return var - k; // 自由变元有var - k个.
    }
    // 3. 唯一解的情况: 在var * (var + 1)的增广阵中形成严格的上三角阵.
    // 计算出Xn-1, Xn-2 ... X0.
    for (i = var - 1; i >= 0; i--){
        temp = a[i][var];
        for (j = i + 1; j < var; j++){
            if (a[i][j] != 0) temp -= a[i][j] * x[j];
        }
        if (temp % a[i][i] != 0) return -2; // 说明有浮点数解，但无整数解.
        x[i] = temp / a[i][i];
    }
    return 0;
}
int main()
{
    //    freopen("in.txt", "r", stdin);
    //    freopen("out.txt","w",stdout);
    int i, j;
    int equ,var;
    while (scanf("%d %d", &equ, &var) != EOF){
        memset(a, 0, sizeof(a));
        for (i = 0; i < equ; i++){
            for (j = 0; j < var + 1; j++){
                scanf("%d", &a[i][j]);
			}
        }
        int free_num = Gauss(equ,var);
        if (free_num == -1) printf("无解!\n");
        else if (free_num == -2) printf("有浮点数解，无整数解!\n");
        else if (free_num > 0){
            printf("无穷多解! 自由变元个数为%d\n", free_num);
            for (i = 0; i < var; i++){
                if (free_x[i]) printf("x%d 是不确定的\n", i + 1);
                else printf("x%d: %d\n", i + 1, x[i]);
            }
        }else{
            for (i = 0; i < var; i++){
                printf("x%d: %d\n", i + 1, x[i]);
            }
        }
        printf("\n");
    }
    return 0;
}