Problem 1. Modify QuickSort algorithm to find the kth largest number: Given k and a sequence of n numbers a1, . . . , an (not sorted), output the kth largest number.
(1) Show the pseudo-code of your algorithm.
\\java代码进行表述
public class QuickSort {
public static void main(String[] args) {
int[] nums;\\定义数组
int top;\\top用来表示k
int topk = topk(nums, 0, nums.length -1, top - 1);
\\打印元素
System.out.println(topk);
}
public static int topk(int[] nums, int start, int end, int k) {
\\正常快排过程,数组第一个元素作为piovt,只是改变了排序顺序,从大到小进行排序,满足后续给出kth大元素
int target = nums[start];
int i = start;
int j = end;
while (i < j) {
\\这里改变比较条件,将大的元素放到piovt前,小的放在后面
while (i < j && nums[j] <= target) j--;
while (i < j && nums[i] >= target) i++;
if (i < j) swap(nums, i, j);
}
swap(nums, start, i);
\\递归调用该函数,直至选中的piovt在交换完位置后在k号位置(下标k-1),此时kth大元素在他正确的位置,否则选择包含kth大元素的划分继续进行划分
if (i < k) return topk(nums, i + 1, end, k);
else if (i > k) return topk(nums, start, i - 1, k);
else return nums[i];
}
public static void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
(2) Prove its expected running time is O(n) by the probability argument about comparing pairs of elements.
根据Thomas H.Cormen,Charles E.Leiserson等人所著《算法导论第三版》的第七章关于快速排序时间复杂度概率算法的介绍(在汉化版的102页附近)讨论该算法时间复杂度。
在原算法中,对于序列
{
z
i
.
.
.
z
j
}
\{z_i ... z_j\}
{zi...zj}中元素
z
i
z_i
zi与
z
j
z_j
zj会进行比较当且仅当其中一个被选为piovt,在此基础上观察(1)中算法,当上一轮进行划分时,不包含kth大元素的划分将被丢弃,如
{
z
i
.
.
.
z
k
.
.
.
z
j
}
z
p
i
o
c
t
{
被丢弃划分
}
\{z_i...z_k...z_j\}z_{pioct}\{被丢弃划分\}
{zi...zk...zj}zpioct{被丢弃划分}
即对于该序列中元素
z
i
z_i
zi与
z
j
z_j
zj会进行比较不仅要求其中一个被选为piovt,还要求该序列内包含kth大元素。根据《算法导论》进行快排时,两个元素进行比较的概率是
2
j
−
i
+
1
\frac{2}{j-i+1}
j−i+12,同时,kth大元素在该序列的概率为该序列长度与原始数组长度的比,也就是
j
−
i
+
1
n
\frac{j-i+1}{n}
nj−i+1,因此基础进行计算
E
[
X
]
=
∑
i
=
1
n
−
1
∑
j
=
i
+
1
n
2
j
−
i
+
1
j
−
i
+
1
n
=
∑
i
=
1
n
−
1
∑
j
=
i
+
1
n
2
n
=
∑
i
=
1
n
−
1
n
−
i
n
=
(
n
−
1
)
(
n
−
1
+
1
)
n
=
O
(
n
)
\begin{aligned} E[X]&=\displaystyle\sum^{n-1}_{i=1}\displaystyle\sum^{n}_{j=i+1}\frac{2}{j-i+1}\frac{j-i+1}{n}\\ &=\displaystyle\sum^{n-1}_{i=1}\displaystyle\sum^{n}_{j=i+1}\frac{2}{n}\\ &=\displaystyle\sum^{n-1}_{i=1}\frac{n-i}{n}\\ &=\frac{(n-1)(n-1+1)}{n}\\ &=O(n) \end{aligned}
E[X]=i=1∑n−1j=i+1∑nj−i+12nj−i+1=i=1∑n−1j=i+1∑nn2=i=1∑n−1nn−i=n(n−1)(n−1+1)=O(n)
Problem 2. Prove that Euclid’s algorithm to compute gcd(m, n) runs in time O(log m+ log n) assuming all integer-operations are done in O(1) time.
假设按轮次递归调用该算法进行辗转相除法,在任意轮次,用a代表较大的数,b代表较小的数,则在该轮运算结束后(进行mod除后,还未交换a与b两数的值),a的值至少会减小为 a 2 \frac{a}{2} 2a,以下证明:
若 a ≥ 2 b a\geq{2b} a≥2b,则 a m o d b < b ≤ a 2 a \quad mod \quad b <b\leq{\frac{a}{2}} amodb<b≤2a;
若 b ≤ a < 2 b b\leq{a}<2b b≤a<2b,则 a − 2 b < 0 ⇒ a 2 − b < 0 ⇒ a − b < a 2 a-2b<0\Rightarrow\frac{a}{2}-b<0 \Rightarrow a-b<\frac{a}{2} a−2b<0⇒2a−b<0⇒a−b<2a,进行模运算后 a m o d b = a − b < a 2 a\quad mod \quad b = a-b<\frac{a}{2} amodb=a−b<2a
显然该算法最坏情况为,输入的m与n互素,最后结果为1,同时每次运算,较大的数仅变为原值的 1 2 \frac{1}{2} 21(经过上面证明该情况取不到,但是作为下限进行证明)。此时从1分别增大到m与n的时间复杂度分别为log m与log n,因此将m与n辗转相除的时间复杂度为O(log m+log n),此为算法下限。
Problem 3. (1) Exercise 14 in Chapter 2 (2nd Edition).
将 ∑ k = 1 n k 2 k \displaystyle \sum^{n}_{k=1}k2^k k=1∑nk2k改写成 ∑ 1 ≤ j ≤ k ≤ n 2 k \displaystyle \sum_{1\leq{j}\leq{k}\leq{n}}2^k 1≤j≤k≤n∑2k进行计算
易知
∑
j
=
1
k
1
=
k
\displaystyle \sum^{k}_{j=1}1 = k
j=1∑k1=k,因此可以将
k
2
k
k2^{k}
k2k理解为k个
2
k
2^k
2k叠加再求和,可将
∑
k
=
1
n
k
2
k
\displaystyle \sum^{n}_{k=1}k2^k
k=1∑nk2k可以改写成
∑
k
=
1
n
∑
j
=
1
k
2
k
\displaystyle \sum^{n}_{k=1} \displaystyle \sum^{k}_{j=1}2^k
k=1∑nj=1∑k2k,根据课本(2.32)进一步变换为即可得到
∑
1
≤
j
≤
k
≤
n
2
k
\displaystyle \sum_{1\leq{j}\leq{k}\leq{n}}2^k
1≤j≤k≤n∑2k,进一步改写该式得到
∑
j
=
1
n
∑
k
=
j
n
2
k
\displaystyle \sum^{n}_{j=1} \displaystyle \sum^{n}_{k=j}2^k
j=1∑nk=j∑n2k,以该式为基础继续计算
∑
j
=
1
n
∑
k
=
j
n
2
k
=
∑
j
=
1
n
(
2
n
+
1
−
2
j
)
等比数列求和
=
n
×
2
n
+
1
−
∑
j
=
1
n
2
j
=
n
×
2
n
+
1
−
2
n
+
1
+
2
\begin{aligned} \displaystyle \sum^{n}_{j=1} \displaystyle \sum^{n}_{k=j}2^k&=\displaystyle \sum^{n}_{j=1}(2^{n+1}-2^j) \quad\quad等比数列求和\\ &=n\times2^{n+1}-\displaystyle \sum^{n}_{j=1}2^j \\ &=n\times2^{n+1}-2^{n+1}+2 \end{aligned}
j=1∑nk=j∑n2k=j=1∑n(2n+1−2j)等比数列求和=n×2n+1−j=1∑n2j=n×2n+1−2n+1+2
(1) Exercise 15 in Chapter 2 (2nd Edition).

利用方法5计算
∑
k
=
1
n
k
3
\displaystyle \sum^n_{k=1}k^3
k=1∑nk3,由于符号输入原因,立方叠加与平方叠加都用
∑
\sum
∑的形式表达,根据题目提示有
∑
k
=
1
n
k
3
+
∑
k
=
1
n
k
2
=
2
∑
1
≤
j
≤
k
≤
n
j
k
=
2
×
1
2
(
(
∑
k
=
1
n
k
)
2
+
∑
k
=
1
n
k
2
)
=
(
∑
k
=
1
n
k
)
2
+
∑
k
=
1
n
k
2
\begin{aligned} \displaystyle \sum^n_{k=1}k^3+\displaystyle \sum^n_{k=1}k^2 &=2\displaystyle \sum_{1\leq{j}\leq{k}\leq{n}}jk\\ &=2\times\frac{1}{2}((\displaystyle \sum^n_{k=1}k)^2+\displaystyle \sum^n_{k=1}k^2)\\ &=(\displaystyle \sum^n_{k=1}k)^2+\displaystyle \sum^n_{k=1}k^2 \end{aligned}
k=1∑nk3+k=1∑nk2=21≤j≤k≤n∑jk=2×21((k=1∑nk)2+k=1∑nk2)=(k=1∑nk)2+k=1∑nk2
两边同时减去
∑
k
=
1
n
k
2
\displaystyle \sum^n_{k=1}k^2
k=1∑nk2有
∑
k
=
1
n
k
3
=
(
∑
k
=
1
n
k
)
2
=
(
(
1
+
n
)
n
2
)
2
\begin{aligned} \displaystyle \sum^n_{k=1}k^3&=(\displaystyle \sum^n_{k=1}k)^2\\ &=(\frac{(1+n)n}{2})^2 \end{aligned}
k=1∑nk3=(k=1∑nk)2=(2(1+n)n)2
Problem 4. (1) Exercise 10 in Chapter 3 (2nd Edition).

证明 ⌈ 2 x + 1 2 ⌉ − ⌈ 2 x + 1 4 ⌉ + ⌊ 2 x + 1 4 ⌋ \lceil \frac{2x+1}{2}\rceil - \lceil \frac{2x+1}{4}\rceil+\lfloor \frac{2x+1}{4}\rfloor ⌈22x+1⌉−⌈42x+1⌉+⌊42x+1⌋总是等于 ⌊ x ⌋ \lfloor x\rfloor ⌊x⌋或 ⌈ x ⌉ \lceil x\rceil ⌈x⌉
只有当 2 x + 1 4 \frac{2x+1}{4} 42x+1为整数时,其的顶与底相等,否则 ( − ⌈ 2 x + 1 4 ⌉ + ⌊ 2 x + 1 4 ⌋ ) = − 1 (- \lceil \frac{2x+1}{4}\rceil+\lfloor \frac{2x+1}{4}\rfloor)=-1 (−⌈42x+1⌉+⌊42x+1⌋)=−1,以此为划分进行讨论
1.当 2 x + 1 4 \frac{2x+1}{4} 42x+1为整数时,即 2 x + 1 4 = k , k ∈ z \frac{2x+1}{4}=k,k\in{z} 42x+1=k,k∈z,此时有 x = 2 k − 1 2 , { x } = 1 2 x=2k-\frac{1}{2},\{x\}=\frac{1}{2} x=2k−21,{x}=21
原式 = ⌈ 2 x + 1 2 ⌉ = ⌈ 4 k − 1 + 1 2 ⌉ = ⌈ 2 k ⌉ = 2 k 原式=\lceil \frac{2x+1}{2}\rceil=\lceil \frac{4k-1+1}{2}\rceil=\lceil 2k\rceil=2k 原式=⌈22x+1⌉=⌈24k−1+1⌉=⌈2k⌉=2k
又因为:
x
=
2
k
−
1
2
,
k
∈
z
x=2k-\frac{1}{2},k\in{z}
x=2k−21,k∈z
所以有:
⌈
x
⌉
=
⌈
2
k
−
1
2
⌉
=
2
k
=
原式
\lceil x \rceil =\lceil 2k-\frac{1}{2}\rceil=2k=原式
⌈x⌉=⌈2k−21⌉=2k=原式
即 x = 2 k − 1 2 , k ∈ z x=2k-\frac{1}{2},k\in{z}\quad x=2k−21,k∈z时,有原式= ⌈ x ⌉ \lceil x \rceil ⌈x⌉
2.当
x
=
2
k
−
3
2
,
k
∈
z
x=2k-\frac{3}{2},k\in{z}\quad
x=2k−23,k∈z时,
x
−
1
2
=
2
k
−
2
=
⌊
x
⌋
x-\frac{1}{2}=2k-2=\lfloor x \rfloor
x−21=2k−2=⌊x⌋,原式有
⌈
2
x
+
1
2
⌉
−
⌈
2
x
+
1
4
⌉
+
⌊
2
x
+
1
4
⌋
=
⌈
2
(
2
k
−
3
2
)
+
1
2
⌉
−
⌈
2
(
2
k
−
3
2
)
+
1
4
⌉
+
⌊
2
(
2
k
−
3
2
)
+
1
4
⌋
=
⌈
4
k
−
3
+
1
2
⌉
−
⌈
4
k
−
3
+
1
4
⌉
+
⌊
4
k
−
3
+
1
4
⌋
=
⌈
4
k
−
3
+
1
2
⌉
−
1
=
2
k
−
2
=
x
−
1
2
=
⌊
x
⌋
\begin{aligned} \lceil \frac{2x+1}{2}\rceil - \lceil \frac{2x+1}{4}\rceil+\lfloor \frac{2x+1}{4}\rfloor&=\lceil \frac{2(2k-\frac{3}{2})+1}{2}\rceil- \lceil \frac{2(2k-\frac{3}{2})+1}{4}\rceil+\lfloor \frac{2(2k-\frac{3}{2})+1}{4}\rfloor\\ &=\lceil \frac{4k-3+1}{2}\rceil- \lceil \frac{4k-3+1}{4}\rceil+\lfloor \frac{4k-3+1}{4}\rfloor\\ &=\lceil \frac{4k-3+1}{2}\rceil- 1\\ &=2k-2\\ &=x-\frac{1}{2}=\lfloor x \rfloor \\ \end{aligned}
⌈22x+1⌉−⌈42x+1⌉+⌊42x+1⌋=⌈22(2k−23)+1⌉−⌈42(2k−23)+1⌉+⌊42(2k−23)+1⌋=⌈24k−3+1⌉−⌈44k−3+1⌉+⌊44k−3+1⌋=⌈24k−3+1⌉−1=2k−2=x−21=⌊x⌋
3.当
0
≤
{
x
}
<
1
2
0\leq\{x\}<\frac{1}{2}
0≤{x}<21时,有
1
2
≤
{
x
+
1
2
}
<
1
\frac{1}{2}\leq\{x+\frac{1}{2}\}<1
21≤{x+21}<1
原式
=
⌈
2
x
+
1
2
⌉
−
1
=
⌈
x
+
1
2
⌉
−
1
=
⌈
x
⌉
−
1
=
⌊
x
⌋
原式=\lceil \frac{2x+1}{2}\rceil -1=\lceil x+\frac{1}{2}\rceil -1=\lceil x\rceil -1=\lfloor x \rfloor
原式=⌈22x+1⌉−1=⌈x+21⌉−1=⌈x⌉−1=⌊x⌋
4.当
1
2
<
{
x
}
\frac{1}{2}<\{x\}
21<{x}时,有
0
<
{
x
+
1
2
}
≤
1
2
a
n
d
⌈
x
+
1
2
⌉
=
⌈
x
⌉
+
1
0<\{x+\frac{1}{2}\}\leq{\frac{1}{2}}\quad and \quad \lceil x+\frac{1}{2} \rceil = \lceil x\rceil+1
0<{x+21}≤21and⌈x+21⌉=⌈x⌉+1
原式
=
⌈
2
x
+
1
2
⌉
−
1
=
⌈
x
+
1
2
⌉
−
1
=
⌈
x
⌉
+
1
−
1
=
⌈
x
⌉
原式=\lceil \frac{2x+1}{2}\rceil -1=\lceil x+\frac{1}{2}\rceil -1=\lceil x\rceil +1-1=\lceil x \rceil
原式=⌈22x+1⌉−1=⌈x+21⌉−1=⌈x⌉+1−1=⌈x⌉
总结:当 1 2 < { x } < 1 \frac{1}{2} <\{x\} <1 21<{x}<1时原式等于$\lceil x \rceil $;当 0 ≤ { x } < 1 2 0 \leq\{ x \} < \frac{1}{2} 0≤{x}<21时原式等于 ⌊ x ⌋ \lfloor x \rfloor ⌊x⌋; x = 2 k − 1 2 , k ∈ z x=2k-\frac{1}{2},k\in{z}\quad x=2k−21,k∈z时,有原式= ⌈ x ⌉ \lceil x \rceil ⌈x⌉; x = 2 k − 3 2 , k ∈ z x=2k-\frac{3}{2},k\in{z}\quad x=2k−23,k∈z时,有原式= ⌊ x ⌋ \lfloor x \rfloor ⌊x⌋;
也就是 { x } = 1 2 \{x\}=\frac{1}{2} {x}=21时,原式等于其最接近的偶数,否则为最接近的整数。
(2) Exercise 23 in Chapter 3 (2nd Edition).

令第n个元素的值为
A
k
A_k
Ak,他在该序列中的位置为n(从1开始计算),可以对序列进行观察得到,
A
k
A_k
Ak的第一个元素之前共有1个1,2个2…
A
k
−
1
A_{k-1}
Ak−1个
A
k
−
1
A_{k-1}
Ak−1,在此之后,有
A
k
A_k
Ak个
A
k
A_k
Ak.为了方便计算,令
A
k
=
m
A_{k}=m
Ak=m,则有第一个值为m的元素位置为:
1
2
(
m
−
1
+
1
)
(
m
−
1
)
+
1
=
1
2
m
(
m
−
1
)
+
1
\frac{1}{2}(m-1+1)(m-1)+1 =\frac{1}{2}m(m-1)+1
21(m−1+1)(m−1)+1=21m(m−1)+1
最后一个元素的位置为:
1
2
m
(
m
−
1
)
+
1
+
(
m
−
1
)
=
1
2
m
(
m
+
1
)
\frac{1}{2}m(m-1)+1+(m-1)=\frac{1}{2}m(m+1)
21m(m−1)+1+(m−1)=21m(m+1)
也就是位置为范围
(
1
2
m
(
m
−
1
)
,
1
2
m
(
m
+
1
)
]
(\frac{1}{2}m(m-1),\frac{1}{2}m(m+1)]
(21m(m−1),21m(m+1)]的范围内,
A
k
A_k
Ak的取值都为m,也就是n的范围在:
1
2
m
(
m
−
1
)
<
n
≤
1
2
m
(
m
+
1
)
\frac{1}{2}m(m-1)<n\leq{\frac{1}{2}m(m+1)}
21m(m−1)<n≤21m(m+1)
不等式同时乘2去除分数有:
m
(
m
−
1
)
<
2
n
≤
m
(
m
+
1
)
m(m-1)<2n\leq{m(m+1)}
m(m−1)<2n≤m(m+1)
又由于m和n都是整数,因此可以在不等式两端添加
1
4
\frac{1}{4}
41凑成平方式有:
m
(
m
−
1
)
+
1
4
<
2
n
<
m
(
m
+
1
)
+
1
4
m(m-1)+\frac{1}{4}<2n<m(m+1)+\frac{1}{4}
m(m−1)+41<2n<m(m+1)+41
此时不等式右侧取不到等于,又由于m与n最小为1,因此不等式三部分都是正数,开方则有
m
−
1
2
<
2
n
<
m
+
1
2
m
<
2
n
+
1
2
<
m
+
1
m-\frac{1}{2}<\sqrt{2n}<m+\frac{1}{2}\\ m<\sqrt{2n}+\frac{1}{2}<m+1
m−21<2n<m+21m<2n+21<m+1
即
A
n
=
m
=
⌊
2
n
+
1
2
⌋
A_n= m = \lfloor \sqrt{2n}+\frac{1}{2} \rfloor
An=m=⌊2n+21⌋ (根据课本3.5,显然不等式左边的不等号并不是
≤
\leq
≤符号也可以得到该结论)
Problem 5. Exercise 28 in Chapter 3 (2nd Edition)

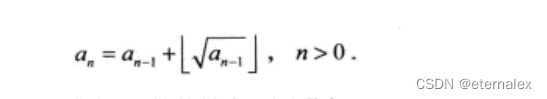
a 0 = 1 , a n = a n − 1 + ⌊ a n − 1 ⌋ a_0=1,a_n=a_{n-1}+\lfloor \sqrt{a_{n-1}} \rfloor a0=1,an=an−1+⌊an−1⌋,求解 a n a_n an的递推式
难以直接看出规律,计算前几项的值如下:
| 序号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 值 | 1 | 2 | 3 | 4 | 6 | 8 | 10 | 13 | 16 | 20 | 24 | 28 | 33 |
| 序号 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 值 | 38 | 44 | 50 | 57 | 64 | 72 | 80 | 88 | 97 | 106 | 116 | 126 | 137 |
可以观察到 a 3 = 4 , a 8 = 16 , a 17 = 64 a_3=4,a_8=16,a_{17}=64 a3=4,a8=16,a17=64,推测存在以 ( 2 k ) 2 (2k)^2 (2k)2为基准的递推关系,通过程序计算可得 a 34 = 256 = ( 2 × 8 ) 2 , a 67 = 1024 = ( 2 × 16 ) 2 , a 132 = 4096 ( 2 × 32 ) 2 a_{34}=256=(2\times8)^2,a_{67}=1024=(2\times16)^2,a_{132}=4096(2\times32)^2 a34=256=(2×8)2,a67=1024=(2×16)2,a132=4096(2×32)2,且每两项之间的下标间隔2k+1。设 2 k = m , 即 a n = m 2 2k = m,即a_n=m^2 2k=m,即an=m2,则有这样的观察:
a n + 2 k + 1 = ( m + k ) 2 + m − k , a n + 2 k + 2 = ( m + k ) 2 + 2 m a_{n+2k+1}=(m+k)^2+m-k,a_{n+2k+2}=(m+k)^2+2m an+2k+1=(m+k)2+m−k,an+2k+2=(m+k)2+2m,
接下来通过数学归纳法证明:
m = 2 时: a 3 = 4 , a 4 = ( 2 + 0 ) 2 + 2 − 0 = 6 , a 5 = ( 2 + 0 ) 2 + 2 × 2 = 8 m=2时:a_3=4,a_4=(2+0)^2+2-0=6,a_5=(2+0)^2+2\times2=8 m=2时:a3=4,a4=(2+0)2+2−0=6,a5=(2+0)2+2×2=8
假设有 a n = m 2 , a n + 2 k + 1 = ( m + k ) 2 + m − k , a n + 2 k + 2 = ( m + k ) 2 + 2 m a_n=m^2,a_{n+2k+1}=(m+k)^2+m-k,a_{n+2k+2}=(m+k)^2+2m an=m2,an+2k+1=(m+k)2+m−k,an+2k+2=(m+k)2+2m成立,证明k+1的情况:
首先有这样的观察, ( k + 1 ) 2 − k 2 = 2 k + 1 (k+1)^2-k^2=2k+1 (k+1)2−k2=2k+1,对于任意 k 2 ≤ a < ( k + 1 ) 2 k^2\leq{a}<(k+1)^2 k2≤a<(k+1)2有 ⌊ a ⌋ = k \lfloor \sqrt{a} \rfloor=k ⌊a⌋=k
当k=0时:
a
n
+
1
=
a
n
+
⌊
a
n
⌋
=
m
2
+
m
a
n
+
2
=
a
n
+
1
+
⌊
a
n
+
1
⌋
=
m
2
+
m
+
⌊
m
2
+
m
⌋
=
m
+
2
m
\begin{aligned} a_{n+1}&=a_n+\lfloor \sqrt{a_n} \rfloor\\ &=m^2+m\\ a_{n+2}&=a_{n+1}+\lfloor \sqrt{a_{n+1}} \rfloor\\ &=m^2+m+\lfloor \sqrt{m^2+m} \rfloor\\ &=m+2m \end{aligned}
an+1an+2=an+⌊an⌋=m2+m=an+1+⌊an+1⌋=m2+m+⌊m2+m⌋=m+2m
成立。
当k≠0时:假设k值为k时成立,则k值为k+1情况证明如下
a
n
+
2
k
+
3
=
a
n
+
2
k
+
1
+
⌊
a
n
+
2
k
+
1
⌋
+
⌊
a
n
+
2
k
+
2
⌋
=
(
m
+
k
)
2
+
m
−
k
+
⌊
(
m
+
k
)
2
+
m
−
k
⌋
+
⌊
(
m
+
k
)
2
+
2
m
⌋
=
(
m
+
k
)
2
+
m
−
k
+
(
m
+
k
)
+
(
m
+
k
)
=
(
m
+
k
+
1
)
2
+
m
−
(
k
+
1
)
a
n
+
2
k
+
4
=
a
n
+
2
k
+
2
+
⌊
a
n
+
2
k
+
2
⌋
+
⌊
a
n
+
2
k
+
3
⌋
=
(
m
+
k
)
2
+
2
m
+
⌊
(
m
+
k
)
2
+
2
m
⌋
+
⌊
(
m
+
k
+
1
)
2
+
m
−
(
k
+
1
)
⌋
=
(
m
+
k
)
2
+
2
m
+
(
m
+
k
)
+
(
m
+
k
+
1
)
=
(
m
+
k
+
1
)
2
+
2
m
\begin{aligned} a_{n+2k+3}&=a_{n+2k+1}+\lfloor \sqrt{a_{n+2k+1}} \rfloor+\lfloor \sqrt{a_{n+2k+2}} \rfloor\\ &=(m+k)^2+m-k+\lfloor \sqrt{(m+k)^2+m-k} \rfloor+\lfloor \sqrt{(m+k)^2+2m} \rfloor\\ &=(m+k)^2+m-k+(m+k)+(m+k) \\ &=(m+k+1)^2+m-(k+1) \\ a_{n+2k+4}&=a_{n+2k+2}+\lfloor \sqrt{a_{n+2k+2}} \rfloor+\lfloor \sqrt{a_{n+2k+3}} \rfloor\\ &=(m+k)^2+2m+\lfloor \sqrt{(m+k)^2+2m} \rfloor+\lfloor \sqrt{(m+k+1)^2+m-(k+1)} \rfloor\\ &=(m+k)^2+2m+(m+k)+(m+k+1) \\ &=(m+k+1)^2+2m \\ \end{aligned}
an+2k+3an+2k+4=an+2k+1+⌊an+2k+1⌋+⌊an+2k+2⌋=(m+k)2+m−k+⌊(m+k)2+m−k⌋+⌊(m+k)2+2m⌋=(m+k)2+m−k+(m+k)+(m+k)=(m+k+1)2+m−(k+1)=an+2k+2+⌊an+2k+2⌋+⌊an+2k+3⌋=(m+k)2+2m+⌊(m+k)2+2m⌋+⌊(m+k+1)2+m−(k+1)⌋=(m+k)2+2m+(m+k)+(m+k+1)=(m+k+1)2+2m
成立。
当k=m时,也就是
a
n
+
2
m
+
1
a_{n+2m+1}
an+2m+1的情况,该元素的值应为
(
2
m
)
2
(2m)^2
(2m)2,证明如下
a
n
+
2
m
+
1
+
(
m
+
m
)
2
+
m
−
m
=
(
2
m
)
2
\begin{aligned} a_{n+2m+1}&+(m+m)^2+m-m=(2m)^2\\ \end{aligned}
an+2m+1+(m+m)2+m−m=(2m)2
因此原假设成立,现在改写成更简单的形式:
1.首先计算值为
(
2
k
)
2
(2k)^2
(2k)2的项的元素下标,将该下标用
b
l
b_l
bl表示,有以下规律:
b
1
=
2
1
+
1
=
3
b
2
=
b
1
+
2
2
+
1
=
8
b
3
=
b
2
+
2
3
+
1
=
17
…
…
…
…
b
l
=
b
l
−
1
+
2
l
+
1
b_1=2^1+1=3\\ b_2=b_1+2^2+1=8\\ b_3=b_2+2^3+1=17\\ …………\\ b_l=b_{l-1}+2^l+1
b1=21+1=3b2=b1+22+1=8b3=b2+23+1=17…………bl=bl−1+2l+1
很容易得到递推关系:
b
l
=
2
l
+
1
+
l
−
2
b_l=2^{l+1}+l-2
bl=2l+1+l−2
2.对于任意 n ∈ ( 2 l + 1 + l − 2 , 2 l + 2 + l − 1 ] n \in (2^{l+1}+l-2,2^{l+2}+l-1] n∈(2l+1+l−2,2l+2+l−1],有上文关于 a n a_n an的递推关系存在,即 a n + 2 k + 1 = ( m + k ) 2 + m − k , a n + 2 k + 2 = ( m + k ) 2 + 2 m a_{n+2k+1}=(m+k)^2+m-k,a_{n+2k+2}=(m+k)^2+2m an+2k+1=(m+k)2+m−k,an+2k+2=(m+k)2+2m,令此处n为 b l b_l bl, 2 k + 1 或 2 k + 2 2k+1或2k+2 2k+1或2k+2为 o f f s e t offset offset,同时可以得到 m = 2 l m=2^{l} m=2l(上面两句的n表示不同含义,第一句的任意n指的是 a n a_n an的下标n,后面的n指的是数列 a n + 2 k + 1 a_{n+2k+1} an+2k+1的递推式的下标中的第一个n,这个n也就是上一步得到的递推关系中的 b l b_l bl,是平方项元素的下标,因此后文中用 b l b_l bl表示).则有
o f f s e t = n − b l = n − 2 l + 1 − l + 2 offset=n-b_l=n-2^{l+1}-l+2 offset=n−bl=n−2l+1−l+2
1)offset为偶数情况:
2 k + 2 = n − 2 l + 1 − l + 2 ⇒ k = n − l 2 − 2 l 2k+2=n-2^{l+1}-l+2 \quad\quad \Rightarrow \quad k=\frac{n-l}{2}-2^l 2k+2=n−2l+1−l+2⇒k=2n−l−2l
则有
a n = a b l + 2 k + 2 = ( m + k ) 2 + 2 m = ( 2 l − 2 l + n − l 2 ) 2 + 2 × 2 l = ( n − l 2 ) 2 + 2 l + 1 a_n=a_{b_l+2k+2}=(m+k)^2+2m=(2^l-2^l+\frac{n-l}{2})^2+2\times 2^l=(\frac{n-l}{2})^2+ 2^{l+1} an=abl+2k+2=(m+k)2+2m=(2l−2l+2n−l)2+2×2l=(2n−l)2+2l+1
2)offset为奇数情况:
2 k + 1 = n − 2 l + 1 − l + 2 ⇒ k = n − l + 1 2 − 2 l 2k+1=n-2^{l+1}-l+2 \quad\quad \Rightarrow \quad k=\frac{n-l+1}{2}-2^l 2k+1=n−2l+1−l+2⇒k=2n−l+1−2l
则有
a
n
=
a
b
l
+
2
k
+
1
=
(
m
+
k
)
2
+
m
−
k
=
(
2
l
−
2
l
+
n
−
l
+
1
2
)
2
+
2
l
−
(
−
2
l
+
n
−
l
+
1
2
)
=
(
n
−
l
+
1
2
)
2
−
n
−
l
+
1
2
+
2
l
+
1
=
(
n
−
l
+
1
2
)
(
n
−
l
−
1
2
)
+
2
l
+
1
=
(
n
−
l
2
)
2
−
1
4
+
2
l
+
1
\begin{aligned} a_n&=a_{b_l+2k+1}\\ &=(m+k)^2+m-k\\ &=(2^l-2^l+\frac{n-l+1}{2})^2+2^l-(-2^l+\frac{n-l+1}{2})\\ &=(\frac{n-l+1}{2})^2-\frac{n-l+1}{2}+2^{l+1}\\ &=(\frac{n-l+1}{2})(\frac{n-l-1}{2})+2^{l+1}\\ &=(\frac{n-l}{2})^2-\frac{1}{4}+2^{l+1} \quad\quad \end{aligned}
an=abl+2k+1=(m+k)2+m−k=(2l−2l+2n−l+1)2+2l−(−2l+2n−l+1)=(2n−l+1)2−2n−l+1+2l+1=(2n−l+1)(2n−l−1)+2l+1=(2n−l)2−41+2l+1
根据递推式,
a
n
与
2
l
+
1
a_n与2^{l+1}
an与2l+1必然为整数,因此
(
n
−
l
2
)
2
−
1
4
(\frac{n-l}{2})^2-\frac{1}{4}
(2n−l)2−41必然也为整数,则有
(
n
−
l
2
)
2
−
1
4
=
⌊
(
n
−
l
2
)
2
⌋
(\frac{n-l}{2})^2-\frac{1}{4}=\lfloor (\frac{n-l}{2})^2 \rfloor
(2n−l)2−41=⌊(2n−l)2⌋(相当于整数加上一个小数的底还是原整数),因此
a
n
=
⌊
(
n
−
l
2
)
2
⌋
+
2
l
+
1
a_n=\lfloor (\frac{n-l}{2})^2 \rfloor+2^{l+1}
an=⌊(2n−l)2⌋+2l+1
验证l=0时, a 1 = 2 , a 2 = 3 a_1=2,a_2=3 a1=2,a2=3也符合该式,总结有:
a 0 = 1 a_0=1 a0=1,
对于 ∀ n > 0 , n ∈ ( 2 l + 1 + l − 2 , 2 l + 2 + l − 1 ] , l ∈ N \forall n >0,n\in (2^{l+1}+l-2,2^{l+2}+l-1],l\in N ∀n>0,n∈(2l+1+l−2,2l+2+l−1],l∈N,有 a n = ⌊ ( n − l 2 ) 2 ⌋ + 2 l + 1 a_n=\lfloor (\frac{n-l}{2})^2 \rfloor+2^{l+1} an=⌊(2n−l)2⌋+2l+1
说明:值为 ( 2 k ) 2 (2k)^2 (2k)2的元素可以理解为 a b l + 2 × 2 l + 1 , a_{b_l+2\times 2^l+1}, abl+2×2l+1,,因此n的范围为左开右闭,也就是认为 a b l 是通过 a b l − 1 + 2 × 2 l − 1 + 1 a_{b_l}是通过a_{b_{l-1}+2\times 2^{l-1}+1} abl是通过abl−1+2×2l−1+1来计算






















 334
334











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








