前言
编程题部分全部经过实际运行,均为有效,文章趋于口语化,有些解释缺乏逻辑严谨性,且编者水平有限,疏漏之处在所难免,恳请读者批评指正,不胜感激。
计2104 Melody
2023年2月28日
大纲
题型:编程题3题,综合题4题。
一、编程题:
1、链表的类型定义;邻接矩阵表示图的类型定义;链接表表示图的类型定义;vector数组表示图的定义和使用方法。
2、链表中结点的插入和删除操作,时间复杂度分析。
3、图的连通分量的计算方法:DFS、BFS和并查集。
4、基于有序序列进行二分查找的实现原理和实现方法,时间复杂度分析。
二、综合题
包括画图、计算和算法描述等方面。
1、广义表的结构图以及广义表的表头、表尾、表长和深度。
2、哈夫曼树的构建步骤、构建过程以及带权路径长的计算方法。
3、最小生成树(Kruskal算法、Prim算法)的一般步骤。有一个图生成最小生成树的过程。
4、二叉查找树中插入和删除一个键值的一般步骤、由一个键值序列生成一棵二叉查找树的过程、在一棵二叉查找树中删除一个键值的过程。
编程题
第一部分
【例】给定 typedef int datatype 编写单向链表,双向链表,循环链表的定义
【解】
-
对于单向链表:
typedef struct clNode
{
datatype data; //数据域
clNode * next; //链域
clNode():next(NULL){}
}* chainList;-
对于双向链表
typedef struct dclNode
{
datatype data; //数据域
dclNode * pre; //前驱链域
dclNode * next; //后继链域
dclNode():pre(NULL),next(NULL){}
}* dchainList;-
对于循环链表
typedef struct clNode
{
datatype data; //数据域
clNode * next; //链域
clNode():next(NULL){}
}* chainList【例】定义以下常量:
const int eNum = 102; //图的顶点数量
typedef string datatype; //图顶点中存放数据信息的类型请描述并用代码表示图的邻接矩阵表示法,并表示下图
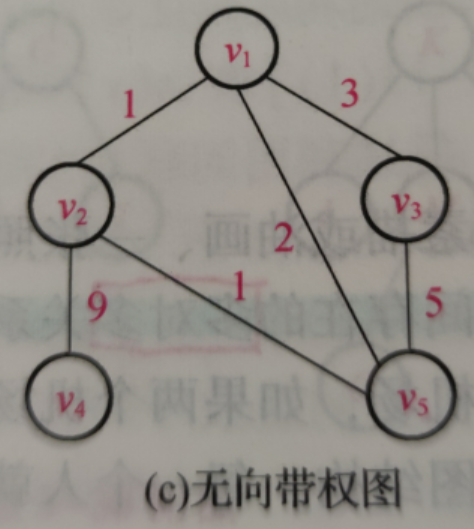
【解】图的邻接矩阵表示法是利用二维数组(矩阵)表示一个图,二维数组中的每一个元素表示相应的两个顶点之间的关系。具体方法是:将图的每个顶点进行编号(从1开始),则二维数组的第 u 行的第 v 个元素表示第 u 个顶点与第 v 个顶点之间的关系。其中不可达用无穷大(INF)表示。题中的图表示如下:
代码定义如下:
struct adjMatrix {
datatype data[eNum]; //顶点的数据信息
int edge[eNum][eNum]; //邻接矩阵
int v; //顶点的数量
int e; //边的数量
};【例】定义以下常量,
const int vNum = 200; //图的边的数量
typedef string datatype; //定义存储的数据类型请描述并用代码表示图的链表表示法,并表示下图

链接表表示法是将图的每一个顶点的邻接点存放一个链表中,因此每一个顶点对应一个链表,所有链表的头结点放在一个数组(edges)中。上图的链表表示法如下:

结点定义如下:
//结点定义
struct vertex {
int u; //邻接点的编号
int w; //权重,无权图可以忽视该属性
vertex* next; //链域
vertex(int _u, int _w) :u(_u), w(_w), next(NULL) {}
};链表定义如下:
typedef struct llNode {
datatype data[vNum]; //顶点的数据信息
vertex* edges[vNum]; //边表
int v; //顶点数
int e; //边数
llNode() :v(0), e(0) {
for (int i = 0; i < vNum; i++)
edges[i] = NULL;
}
}*linkList;【例】请用代码表示图的vector表示法,并说明如何使用
【解】
代码如下:
int v; //定点数
vector<int>g[vNum]; //无权图
vector<pair<int,int>>g1[vNum]; //有权图,pair中的first表示邻接点,second表示权重举例:向图 g 中添加一个 u→v 的有向边
g.edges[u].push_back(v);举例:向图 g 中添加一个 u→v 权重为 w 的有向边
g.edges[u].push_back(make_pair(v,w));第二部分
【例】给定链表定义:
typedef int datatype;
typedef struct clNode
{
datatype data; //数据域
clNode * next; //链域
clNode():next(NULL){}
}* chainList;编写函数 void cl_insert(chainList &h,datatype x,datatype y),在链表 h 中第一个值为 x 的结点后面插入值为 y 的结点,如果 h 中不存在值为 x 的结点,则将 y 的结点插入链表的末尾,并分析复杂度
【解】由于插入操作最多遍历一次整个链表,因此时间复杂度为O(n)
void cl_insert(chainList &h, datatype x, datatype y) {
chainList head = h; // 保存头结点
chainList q = new clNode; // 为q动态存储空间,并指定其数据域的值为x;
q->data = y;
//这里可写可不写,主要是为了严谨不报错,只要不传个空表就没事
if (h == NULL) {
h = new clNode;
h->next = q;
return;
}
//先找到值为x的结点,若不存在则指向最后一个结点
while (h->next != NULL) {
if (h->data == x) {
break;
}
h = h->next;
}
q->next = h->next;
h->next = q;
h = head;
}【解析】这里要保存头结点,因为是按引用传的 h ,在插入之后h就变成指向插入的那个结点了,前面的全都不见了,所以要在找完之后把h重新指向头结点。插入步骤大致为:先用while循环找到值为x的点,如果找到了,则指向值为x的点,找不到则指向最后一个结点,这样可以保证能把next指针串联起来
【例】给定链表定义:
typedef int datatype;
typedef struct clNode
{
datatype data; //数据域
clNode * next; //链域
clNode():next(NULL){}
}* chainList;编写函数 void cl_delete(chainList &h,datatype x) ,删除链表 h 中所有值为 x 的结点,并分析复杂度
【解】由于删除操作最多遍历一次整个链表,因此时间复杂度为O(n)
void cl_delete(chainList& h, datatype x) {
chainList head = h; // 保存头结点
//这里可写可不写,主要是为了严谨不报错,只要不传个空表就没事
if (h == NULL) {
return;
}
//先找到值为x的上结点,若不存在则指向最后一个结点
while (h->next != NULL) {
if (h->next->data == x) {
chainList tmp = h->next; //保存要删的结点
h->next = h->next->next; //上结点指向要删的结点的next
delete tmp; //删了结点
continue; //因为已经next过了跳过下面
}
h = h->next;
}
h = head; // 重新定位头结点
}【解析】head同上。这里操作跟插入差不多,只不过将删除放在了while循环中,关键是要写 continue 因为在if中已经next过一次了,再执行下面的next会导致链表跳了两下,不仅会少判断一半的结点,还会造成空指针访问。
第三部分
【例】编写函数 int ccn_dfs(vector<datatype>g[vNum],int v) 利用DFS算法计算vector数组表示法的无向图 g 的连通分量的数量,结果作为返回值

【解】
bool vis[vNum]; //标记每一个顶点的颜色
//对图g的顶点cur所在的连通分量进行深度优先搜索,初始出发顶点为cur
void dfs(vector<datatype>g[vNum], int v) {
vis[v] = true; //将v涂成黑色
for (int i = 0; i < g[v].size(); i++) {
if (!vis[g[v][i]]) //若为白色邻接点
dfs(g, g[v][i]); //选择继续搜索
}
}
int ccn_dfs(vector<datatype>g[vNum],int v) {
int res = 0;//连通分量数
for (int i = 1; i <= v; i++) {
if (!vis[i]) {
res++;
dfs(g, i);
}
}
return res;
}【解析】无向图的连通分量数就是DFS的使用次数,这里不是说DFS递归的次数,而是每次DFS完了又要找下一个点DFS的次数。
【例】编写函数 int ccn_bfs(vector<datatype>g[vNum],int v) 利用BFS算法计算vector数组表示法的无向图 g 的连通分量的数量,结果作为返回值

【解】
bool vis[vNum]; //标记顶点的颜色
int cnt = 0;
void bfs(vector<datatype>g[vNum], int cur) {
datatype v, u;
queue<int>q; //用队列保存顶点
vis[cur] = true;
q.push(cur); //将初始出发点加入队列
while (!q.empty()) {
u = q.front(); //将顶点提出来
q.pop(); //提出来之后就删了
for (int i = 0; i < g[u].size(); i++) {
v = g[u][i];
if (!vis[v]) { //顶点v为白色
vis[v] = true; //加入队列前将v设置为黑色
q.push(v); //将v加入队列
}
}
}
}
int ccn_bfs(vector<datatype>g[vNum], int v) {
int res = 0;
for (int i = 1; i <= v; i++)
if (!vis[i]) {
res++;
bfs(g, i);
}
return res;
}【解析】无向图的连通分量数就是BFS的使用次数,这里不是说BFS递归的次数,而是每次BFS完了又要找下一个点BFS的次数。
【例】编写函数 int ccn_ds(vector<datatype>g[vNum],int v) 利用并查集算法计算vector数组表示法的无向图 g 的连通分量的数量,结果作为返回值

【解】
struct mqNode
{
int pa;
datatype data;
mqNode() :pa(-1) {}
}mq[vNum];
int find(int x) //查找结点 x的根结点
{
if (mq[x].pa == -1) return x; //递归出口:x的上级为x本身,即x为根结点
return mq[x].pa = find(mq[x].pa); //此代码相当于先找到根结点 rootx,然后pre[x]=rootx
}
void join(int x, int y)
{
x = find(x);
y = find(y);
if (x != y)
mq[x].pa = y;
}
int ccn_ds(vector<datatype>g[vNum], int v) {
int res = 0;
for (int i = 1; i <= v; i++) {
for (int j = 0; j < g[i].size(); j++) {
join(i, g[i][j]);
}
}
for (int i = 1; i <= v; i++) {
if (mq[i].pa == -1) {
res++;
}
}
return res;
}【解析】连通分量的个数就是并查集生成树的数量,只需要统计树的根节点有多少个就行,而根节点的特点是父节点 pa = -1
第四部分
【例】请阐述基于有序序列进行二分查找的实现原理和实现方法,并进行时间复杂度分析
【解】
(1)实现原理:是一种分治算法:将位于顺序表中间的键值与查找键值比较,如果两者想相等,则查找成功;否则以中间元素为分割点,将表分为两个子表,然后在子表中重复上述操作。
(2)实现方法:实现步骤如下:
-
定义整型变量 left 和 right,分别表示表的左端点和右端点,初始为0和n-1
-
若 left > right 说明子表为空,查找失败,结束。否则比较中间元素:令
mid=(left+right)/2:2.1
sl[mid] ==k查找成功,结束2.2
sl[mid] >k说明查找元素应在左半区间,令right =mid-1重复第2步2.3
sl[mid] <k说明查找元素应在右半区间,令left = mid+1重复第2步
(2.1)基于递归的二分查找实现:
int binary_search(vector<keytype>sl, int left, int right, keytype k) {
if (left > right)
return -1;
int mid = (left + right) / 2;
if (sl[mid] == k)
return mid;
if (sl[mid] > k)
return binary_search(sl, left, mid - 1, k);
else
return binary_search(sl, mid + 1, right, k);
}(2.2)基于非递归的二分查找实现:
int binary_search(vector<keytype>sl, keytype k) {
int left = 0;
int right = sl.size() - 1;
int mid;
while (left <= right) {
mid = (left + right) / 2;
if (sl[mid] == k)
return mid;
if (sl[mid] > k)
right = mid - 1;
else
left = mid + 1;
}
return -1; //left > right
}(3)复杂度分析:每次比较后范围缩小一半。设一共经过 x 轮查找,每轮的长度为 \frac{n}{2^x} ,假设最坏的情况下在子表长度为1的时候找到该键值,则
因此时间复杂度为 O(logn)
综合题
第一部分
【例】给出广义表 (a,(b,c),(d,e,((f,g),h)))
(1)广义表的原子结构由哪几部分组成?
(2)请写出广义表的表头,表尾,表长以及深度
(3)请画出该广义表的结构图
【解】
(1)原子结构由3部分组成:tag 标记位、ele 元素、 next指针
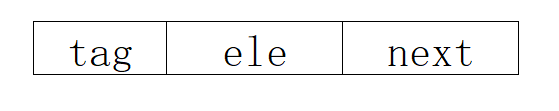
(2)广义表的表头为 a ,表尾为 ( (b,c),(d,e,((f,g),h) ) ,表长为 3 ,深度是 4
(3)结构图为:

第二部分
【例】给定集合\{ 7,19,4,6,32,5,21,30\} ,回答下列问题:
(1)什么是带权路径长度,什么是树的带权路劲长?
(2)哈夫曼树的构建步骤是什么?
(3)根据集合构建哈夫曼树,要求写出构建过程
(4)计算该哈夫曼树的带权路径长
(5)哈夫曼树的结点数为多少?为什么?
【解】
(1)带权路劲长度是结点到该结点之间的路径长度与该结点的权的乘积,树的带权路经长是所有叶子结点的带权路径长度之和
(2)哈夫曼树的构建步骤如下:
-
初始化:将集合中的 m 个值作为 m 个叶结点的权重,并将每个叶结点看做一个二叉树T_i ,于是得到关于二叉树集合 F={}
-
取出与加入:新建一个结点 tmp ,取出集合中最小和次小的两颗二叉树 T_i 和 T_j 分别作为 tmp 的左右子树,然后将结点 tmp 加入到集合中
-
重复第2步,直到二叉树集合中只有一颗树为止,则该树为哈夫曼树
(3)构建过程如下:
-
初始化:

-
取 4 和 5 建立新结点并加入到集合中

-
取 6 和 7 建立新结点并加入到集合中

-
取 9 和 13 建立新结点并加入到集合中

-
取 19 和 2 建立新结点并加入到集合中

-
取 22 和 30 建立新结点并加入到集合中

-
取 32 和 40 建立新结点并加入到集合中

-
取 52 和 72 建立新结点并加入到集合中

构建完成。
(4)带权路经长
(5)结点数为15,因为每次结合减少一个二叉树,则一共需要结合7次,每次产生一个新结点,因此结点数为 8+7=15次
【例】给定叶子结点的权值集合{10, 4, 8, 9, 7, 12, 16, 23},构造相应的哈夫曼(霍夫曼)树,并计算其带权路径长度。
【解】(懒了,不想再画了,贴个网上找到的答案吧,另外,谢谢你的阅读🥰)

带权路经长= (4+7)×4+(10+8+9+12+16)×3+23×2=255
第三部分
【例】下图是一个无向带权图,利用Kruskal算法求其最小生成树,要求如下:

(1)简要说明Kruskal算法的基本思想,重点说明什么情况下某条边会被加入到生成树中,并说明在实现时用什么方法判断。
(2)画出利用Kruskal算法求给定图的最小生成树的过程,要求画出每添加一条边的中间图,并注明加入和舍弃某条边的理由。
【解】
(1)Kruskal算法的思想:每一步都考察权重最小的边 (u,v) ,本质上是一种贪心算法
什么条件下某条边加入:按权重从小到大排序,考虑每一条边:如果该边的两个顶点 u 和 v 不属于最小生成树的同一颗子树,则将边 (u,v) 加入最小生成树中。
实现方法:将每一条边存入数组中根据权重排序,依次从小到大判断每一条边,利用并查集的方法判断两点是否为同一子树,若不属于则使用合并操作
(2)过程如下:

依次考虑 [E,F],[D,F],[B,D],[B,F],[A,B],[A,E],[C,E],[A.C],[C,D]

依次加入EF,DF,BD边,因为E,F,D,B 不在同一子树
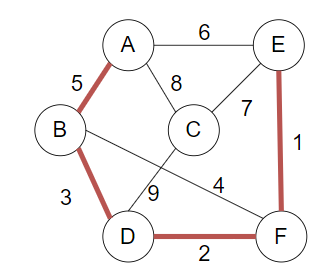
下一步考察BF边,由于BF此时在同一子树,故不加入,考察AB边,AB不属于同一子树,加入

下一步考察AE边,AE属于同一子树,故不加入,考察CE边,CE不属于同一子树,加入
最小生成树构建完成

【例】下图是一个无向带权图,利用Prim算法求其最小生成树,要求如下:

(1)简要说明Prim算法的基本思想,重点说明什么情况下某条边会被加入到生成树中,并说明在实现时用什么方法判断。
(2)画出利用Prim算法求给定图的最小生成树的过程,要求画出每添加一条边的中间图
【解】
(1)Prim算法的基本思想:每次选取一个到最小生成树距离最短的点加入最小生成树并更新其他点的距离,是一种贪心算法
什么条件下某条边加入:选取到最小生成树的距离最小时的顶点
实现方法:构建存放边的小顶堆(priority_queue)每次将最小生成树与邻接点的边加入小顶堆中,每次将权重最小的边对应的顶点加入最小生成树中
(2)构建过程如下
选取A加入最小生成树,选取AB边,并利用B更新距离

选取D加入最小生成树,并利用D更新距离

选取F加入最小生成树,并利用F更新距离

选取E加入最小生成树,并利用E更新距离

最后加入C

构建完成
第四部分
【例】请描述二叉查找树插入和删除一个键值的步骤
【解】
-
插入:插入结点从根结点出发,进行键值比较最终找到可以插入的叶结点
比较结点键值 k 与待插入键值 k_1:
-
如果 t 为空,则找到了位置,创建 t ,令键值为 k ,结束,否则对比 t 的键值 k_1 与 k
1.1 k<k_1:说明要插入的结点在左子树,跳到左子树重复第1步
1.2 k>k_1:说明要插入的结点在右子树,跳到右子树重复第1步
1.3 k=k_1:说明已存在结点,插入失败
-
-
删除:删除结点前先查找到该结点,然后根据中根序列将结点转变成删除直接后继/前驱,最终转变成删除叶结点
-
查找该结点
1.1 该结点为叶结点,则直接删除,删除结束。
1.2 不为叶结点,且右子树不为空,这时转为删除直接后继,寻找右子树的最左结点,并取代该结点,重复第1步
1.3 不为叶结点,且右子树为空,将左孩子(左子树的根节点)取代该结点,并转为删除左孩子,重复第1步
-
【例】依次将键值序列 中的每个键值插入到一棵二叉查找树bst中,完成下列各题:
-
通过画图说明二叉查找树bst的产生过程。
-
写出二叉查找树bst的中根序列
-
通过画图说明二叉查找树删除键值为15的结点的操作过程
【解】(1)

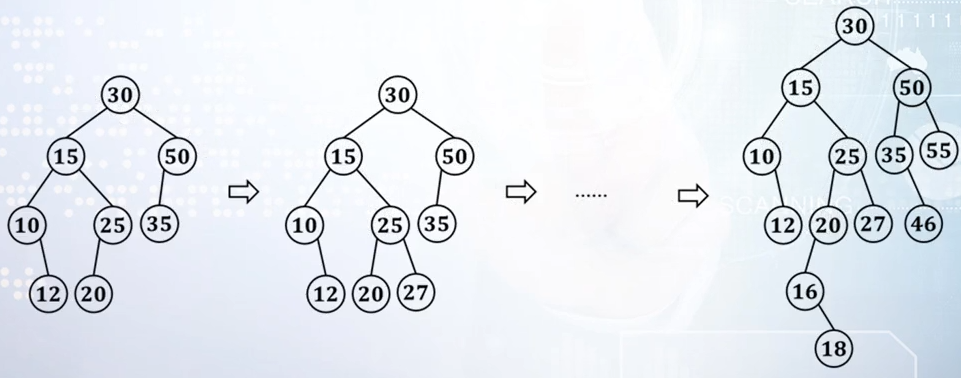
(2)bst的中根序列为: 10,12,15,16,18,20,25,27,30,35,46,50,55
(3)
























 286
286

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








