数字逻辑笔记
——made by njtech_计2104 Melody

引言
这篇笔记于2023年5月25日开始编写,于28日21:54:29完成所有骨架部分,剩下的重心会转向对题型的补充和知识点的再整理。在这篇笔记的背后,我有太多想感谢的人,是他们陪伴我的白天与黑夜的见证。在编写的过程中曾不止一次想过要放弃,但他们时刻鼓舞着我不要放弃,在各个方面为我提供了支持和帮助
因此,我觉得这篇笔记并不只是一份学习资料,它更是一段珍贵的记忆,一段我们一起攀爬知识峰峦,一起探索知识海洋的旅程。在这个过程中,你们的鼓励、支持、以及宝贵的建议,都让我受益良多。而我所能做的,就是将你们的精神,在这篇笔记中继续燃烧,希望它能照亮更多同在学习路上的朋友。你们的无私与大爱,让我明白,学习并非孤独的旅程,而是一条连接彼此,共享知识,共同进步的道路。
以下是感谢名单(不分排名先后)
平安甘喜乐
玉貔貅
Isecom!
四十二万岁
怪苏黍
清枫与酒
椿
AAA建材批发顾
云乐
Ternura
月蓟
及汝
\begin{array}{ccc ccc} \text{平安甘喜乐} & \text{玉貔貅} & \text{Isecom!} & \text{四十二万岁} & \text{怪苏黍} & \text{清枫与酒} \\ \text{椿} & \text{AAA建材批发顾} & \text{云乐} & \text{Ternura} & \text{月蓟} & \text{及汝} \\ \text{} & \text{} & \text{} & \text{} & \text{} & \text{} \\ \end{array}
平安甘喜乐椿玉貔貅AAA建材批发顾Isecom!云乐四十二万岁Ternura怪苏黍月蓟清枫与酒及汝
考试大纲(待整理)
第一章 基本知识
- 进制互转:二进制、八进制、十进制、十六进制之间的转换(送分题)
- 编码方案:格雷码,8421 码 余321
- 常见码:原码反码补码 负数
第二章 逻辑代数基础
- 逻辑代数、复合逻辑、卡诺图(直接考或者结合逻辑电路大题考)
- 代入、反演、对偶规则
(逻辑代数 很重要 直白的就是代数法化简 卡诺图如何表示函数 画图去解对应与或式 )
第三章 集成门电路与触发器
- 各触发器的工作原理(图,与非门还是或非门不要搞错)(ss 同步ss 架空 5个角度去描述)(触发器之间的??转换??)
- 次态方程、约束方程、逻辑功能,各触发器之间的相互转换
(符号 为重点 怎么画 功能是什么 表达式是什么 )
第四章 组合逻辑电路
- 电路分析
- 电路设计
- 竞争与险象的产生、判断和消除
第五章 同步时序逻辑电路
- 电路的描述方法:表达式、状态表、状态图、时间图或波形图
- 电路分析与设计(设计 可以从头到尾 1.根据逻辑问题画出原式状态图 2.根据原始状态图 去隐含表法画??? 3.化简后的状态进行二进制编码 4.用卡诺图配合选择的触发器去实现触发器的驱动方程和输出方程 5.画电路图)
第六章 异步时序逻辑电路
- 电路的分析(只考分析不考设计)
第七章 中规模通用集成电路及其应用
- 常用电路:二进制并行加法器、译码器、编码器、多路选择器、电路分配器、双时针4位二进制同步可逆计数器74193及转换成模小于16的计数器(书上例题)、集成定时器555的三个应用多谐振荡器
(中规模时序电路只考74193 注意:1.异步 暂态过渡 高位 2.其他转换)
(组合逻辑中规模:加法器(超前进位 全加器串行 ) 74138译码器 带优先级的编码器74142 数据选择器 数据分配器 要注意主线:函数发生器)
第一章 基本知识
名词概念
-
基数:计数制中需要用到的数字的个数。例如:在十进制中,需要用到十个数字(0-9),因此十进制的基数是“10”
-
位权:表明不同数位上数值大小的一个固定常数,见下表:
名称 万 千 百 十 个 数位 n n n 5 5 5 4 4 4 3 3 3 2 2 2 1 1 1 位权 1 0 n − 1 10^{n-1} 10n−1 1 0 4 10^4 104 1 0 3 10^3 103 1 0 2 10^2 102 1 0 1 10^1 101 1 0 0 10^0 100 -
并列表示法:又称位置计数法,其表达式为
( N ) R = ( K n − 1 K n − 2 ⋯ K 1 K 0 ⋅ K − 1 K − 2 ⋯ K − m ) R (N)_R=\left(K_{n-1} K_{n-2} \cdots K_1 K_0 \cdot K_{-1} K_{-2} \cdots K_{-m}\right)_R (N)R=(Kn−1Kn−2⋯K1K0⋅K−1K−2⋯K−m)R
例如: ( 1234 ) 10 = ( 1234 ) 10 (1234)_{10}=(1 2 3 4)_{10} (1234)10=(1234)10 -
多项式表示法:又称按权展开法,其表达式为
( N ) R = K n − 1 × R n − 1 + K n − 2 × R n − 2 + ⋯ + K 1 × R 1 + K 0 × R 0 + K − 1 × R − 1 + K − 2 × R − 2 + ⋯ + K − m × R − m = ∑ i = − m n − 1 K i R i \begin{aligned} (N)_R= & K_{n-1} \times R^{n-1}+K_{n-2} \times R^{n-2}+\cdots+K_1 \times R^1+K_0 \times R^0 \\ & +K_{-1} \times R^{-1}+K_{-2} \times R^{-2}+\cdots+K_{-m} \times R^{-m} \\ = & \sum_{i=-m}^{n-1} K_i R^i \end{aligned} (N)R==Kn−1×Rn−1+Kn−2×Rn−2+⋯+K1×R1+K0×R0+K−1×R−1+K−2×R−2+⋯+K−m×R−mi=−m∑n−1KiRi
例如: ( 1234 ) 10 = 1 × 1 0 4 + 2 × 1 0 3 + 3 × 1 0 2 + 4 × 1 0 1 (1234)_{10}=1\times10^4 + 2\times10^3 + 3\times10^2 + 4\times10^1 (1234)10=1×104+2×103+3×102+4×101
进制转换
二进制转十进制
很简单,直接将二进制按权展开即可,如
( 10110.101 ) 2 = 1 × 2 4 + 1 × 2 2 + 1 × 2 1 + 1 × 2 − 1 + 1 × 2 − 3 = 16 + 4 + 2 + 0.5 + 0.125 = ( 22.625 ) 10 \begin{aligned} (10110.101)_2 & =1 \times 2^4+1 \times 2^2+1 \times 2^1+1 \times 2^{-1}+1 \times 2^{-3} \\ & =16+4+2+0.5+0.125 \\ & =(22.625)_{10} \end{aligned} (10110.101)2=1×24+1×22+1×21+1×2−1+1×2−3=16+4+2+0.5+0.125=(22.625)10
十进制转二进制
要对整数和小数分别进行处理。其中,整数部分采用除2取余法,小数部分采用乘2取整法
对于整数,取余法在学习生涯中已学过,不再赘述。
以45为例,计算过程如下:

即 ( 45 ) 10 = ( 101101 ) 2 (45)_{10}=(101101)_2 (45)10=(101101)2
对于小数,所谓乘2,指的是每次都 把小数部分取出来乘2 ,得到个位数部分,然后再 把小数部分取出来乘2:
以0.6875为例,计算过程如下:

不是所有的小数都能被转化成二进制,采用 0舍1入
以0.323为例,计算过程如下:
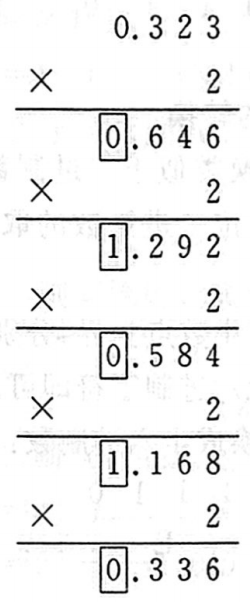
所谓 0舍1入 其实就是四舍五入的变种,即“如果是0则舍去,如果是1则进一位”
对于 ( 0.01010 ) 2 (0.01010)_2 (0.01010)2 ,0舍1入的结果就是 ( 0.0101 ) 2 (0.0101)_2 (0.0101)2
二进制转八、十六进制
首先,你要明白一些恒等式:
2
3
=
8
1
2
4
=
1
6
1
2^3=8^1 \\ 2^4 = 16^1
23=8124=161
你只需要理解一个感觉:”二进制的3(就是式子里的次幂数)就是八进制的1(就是式子里的次幂数),二进制的4就是十六进制的1“。然后再来理解下面的转换:
( 101 001 ) 2 ⟶ ( 51 ) 8 ( 1010 0001 ) 2 ⟶ ( A 1 ) 16 \begin{aligned} (101 \space 001)_2 &\longrightarrow (51)_8 \\ (1010 \space 0001)_2 & \longrightarrow (\mathrm{A}1)_{16} \end{aligned} (101 001)2(1010 0001)2⟶(51)8⟶(A1)16
二进制转八进制其实很简单,只需要将数字按3个3个分 然后把每部分的数值按转成十进制(之所以说十进制是方便理解)然后以此填入即可,例如上式中,“101”转过来就是“5”,“001”转过来就是“1”,所以八进制下的数值就是“51”,十六进制同理
三码:原码补码反码
带符号的计算机码
在计算机中,需要有一位来表示数值的正负情况,因此人们约定为:在数值前有一个符号位,其0表示正,其1表示负

例如,“+1011”的表示为“01101”,“-1101”的表示为“11101”.
这种表示法叫做机器码,下面介绍的原码,反码,补码都是机器码
原码
在上文已经介绍过,原码就是单纯的在前面加了一个符号位
反码
正数反码与原码完全相同,负数反码的数值位按位取反
- “1011”的反码为“1011”
- “[1]1.01"的反码为"[1]0.10"
补码
正数补码与原码完全相同,负数补码的数值位按位取反后再加1
-
“1011”的反码为“1011”
-
“[1]1.01"的反码为"[1]0.11"
为什么计算机要使用补码?
待补充。。。这部分很想写的 但是写不完了
编码方案
BCD码
众所周知,
2
3
=
8
2^3=8
23=8 而
2
4
=
16
2^4 =16
24=16 也就是说理论上4位二进制 可以表示十位数里面的十个数字,这就是BCD(Binary Coded Decimal)码的由来。为了方便使用十进制,通常限定每4位代表一个数字,例如:
0001
0002
⟶
(
12
)
10
\begin{aligned} 0001\space 0002 &\longrightarrow (12 )_{10} \\ \end{aligned}
0001 0002⟶(12)10
下面将介绍8421码,2421码,余3码以及可靠性编码
十进制字符
8421
码
2421
码
余
3
码
0
0000
0000
0011
1
0001
0001
0100
2
0010
0010
0101
3
0011
0011
0110
4
0100
0100
0111
5
0101
1011
1000
6
0110
1100
1001
7
0111
1101
1010
8
1000
1110
1011
9
1001
1111
1100
\begin{array}{c|c|c|c} \hline \text { 十进制字符 } & 8421 \text { 码 } & 2421 \text { 码 } & \text { 余 } 3 \text { 码 } \\ \hline 0 & 0000 & 0000 & 0011 \\ 1 & 0001 & 0001 & 0100 \\ 2 & 0010 & 0010 & 0101 \\ 3 & 0011 & 0011 & 0110 \\ 4 & 0100 & 0100 & 0111 \\ 5 & 0101 & 1011 & 1000 \\ 6 & 0110 & 1100 & 1001 \\ 7 & 0111 & 1101 & 1010 \\ 8 & 1000 & 1110 & 1011 \\ 9 & 1001 & 1111 & 1100 \\ \hline \end{array}
十进制字符 01234567898421 码 00000001001000110100010101100111100010012421 码 0000000100100011010010111100110111101111 余 3 码 0011010001010110011110001001101010111100
8421码
在上文已经介绍过,这就是最常见的BCD码:
(
258
)
10
=
(
0010
0101
1000
)
8421
码
(
0001
0010
0000
1000
)
8421
码
=
(
1208
)
10
\begin{aligned} & (258)_{10}=(0010\space0101\space1000)_{8421 码} \\ & (0001\space0010\space0000\space1000)_{8421 码}=(1208)_{10} \\ & \end{aligned}
(258)10=(0010 0101 1000)8421码(0001 0010 0000 1000)8421码=(1208)10
2421码
所谓2421意思就是4位二进制权重分别为 2 4 2 1.例如
(
1101
)
2421
码
=
1
×
2
+
1
×
4
+
0
×
2
+
1
×
1
=
(
7
)
10
(1101)_{2421码}= 1\times2 +1\times4 +0\times 2 +1\times1 =(7)_{10}
(1101)2421码=1×2+1×4+0×2+1×1=(7)10
在4位二进制中,一共有16个数字,为保证和十进制一一对应,不允许出现 0101~1010 的6种状态
在2421码中存在一种特性,那就是 对9的自补代码 举个例子,4对9的补数是5,将4的2421码 ( 0100 ) (0100) (0100) 取反得到 ( 1011 ) (1011) (1011) 得到的2421码为 5的2421码
余3码
余3码其实就是在8421码的基础上每个码加3,比如 ( 0000 ) 8421 码 = ( 0011 ) 余 3 码 (0000)_{8421码}=(0011)_{余3码} (0000)8421码=(0011)余3码
可靠性编码
以8421码为例,对于数字0和8的8421码
(
0
)
10
=
(
0000
)
8421
码
(
8
)
10
=
(
1000
)
8421
码
(0)_{10} = (0000)_{8421码}\\ (8)_{10} = (1000)_{8421码}
(0)10=(0000)8421码(8)10=(1000)8421码
看起来挺好的,但现实是计算机也是会出错的,可能某个电压不稳定,可能有灰,可能什么磁场影响,一下子在某位数上跳了一下 从0变成了1,那么数值就发生了改变,从0变成了8,在实际生产中,为了减小这种错误带来的影响,我们要寻求一种编码能做到“减少出错后带来的影响” ,这就是可靠性编码。
请注意:可靠性编码不一是BCD码,它主要研究在计算机中的编码
格雷码
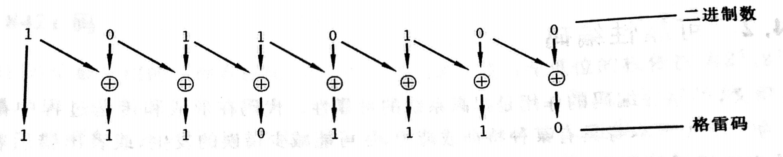
格雷码的核心思想就是“任意两个相邻数之间仅有一位不同”,要实现这种思想,则需要用到异或运算“ ⊕ \oplus ⊕”具体计算见下例。
二进制数 10110100 10110100 10110100 对应的格雷码为 11101110 11101110 11101110 转换过程如下:
奇偶校验码
所谓校验码 就是在原来的码前面再加一位专门用来校验是否出错的校验位的码,根据奇偶可以分成两种,奇校验码和偶校验码。
奇校验码保证信息位和校验位的“1”的个数加起来是奇数,偶校验码保证信息位和校验位的“1”的个数加起来是偶数
信息位
采用奇校验的校验位
采用偶校验的校验位
1
0
0
1
1
0
1
1
0
\begin{array}{c|c|c} \hline \text { 信息位 } & \text { 采用奇校验的校验位 } & \text { 采用偶校验的校验位 } \\ \hline 1\space 0\space 0\space 1\space 1\space 0\space 1 & 1 & 0 \\ \end{array}
信息位 1 0 0 1 1 0 1 采用奇校验的校验位 1 采用偶校验的校验位 0
很显然,如果同时出两个错的话(有两个“1”变成了“0”或者一个“0”变成了“1”或者两个“0”变成了“1”),奇偶校验码无法判断,后面有更高级的校验方式,不过这不在考试范围内了,详细可参考浮梁卖茶人的视频【硬件科普】ECC内存是如何发现错误并纠正的?
第二章 逻辑代数基础
逻辑代数
逻辑代数 L \mathrm{L} L 是一个封闭的代数系统,记为 L = { K , + , ⋅ , − , 0 , 1 } \mathrm{L}=\{\mathrm{K},+,\cdot,-,0,1 \} L={K,+,⋅,−,0,1} ,其中 K \mathrm{K} K 为逻辑变量集 ,满足下列公理
| 公理 | 式子1 | 式子2 |
|---|---|---|
| 交换律 | A + B = B + A \mathrm{A+B=B+A} A+B=B+A | A ⋅ B = B ⋅ A \mathrm{ A\cdot B=B\cdot A} A⋅B=B⋅A |
| 结合律 | ( A + B ) + C = A + ( B + C ) \mathrm{(A+B)+C=A+(B+C)} (A+B)+C=A+(B+C) | ( A ⋅ B ) ⋅ C = A ⋅ ( B ⋅ C ) \mathrm{(A\cdot B)\cdot C=A\cdot (B\cdot C)} (A⋅B)⋅C=A⋅(B⋅C) |
| 分配律 | $ \mathrm{A+(B\cdot C)=(A+B)\cdot (A+C)}$ | A ⋅ ( B + C ) = A ⋅ B + A ⋅ C ) \mathrm{ A\cdot (B+ C)=A\cdot B+A\cdot C)} A⋅(B+C)=A⋅B+A⋅C) |
| 0 - 1律 |
A
+
0
=
A
\mathrm{A+0=A}
A+0=A A + 1 = 1 \mathrm{A+1=1} A+1=1 |
A
⋅
0
=
0
\mathrm{A\cdot0=0}
A⋅0=0 A ⋅ 1 = A \mathrm{A\cdot 1=A} A⋅1=A |
| 互补律 | A + A ˉ = 1 \mathrm{A+\bar{A}=1 } A+Aˉ=1 | A ⋅ A ˉ = 0 \mathrm{A\cdot\bar{A}=0 } A⋅Aˉ=0 |
每个逻辑变量之间满足 或 与 非 运算,不再阐述
逻辑函数的三种表示法
逻辑函数指的是某个逻辑电路输入逻辑变量后得到输出变量的这一转换关系
F
=
f
(
A
1
,
A
2
,
⋯
,
A
n
)
F=f(\mathrm{A_1,A_2,\cdots ,A_n})
F=f(A1,A2,⋯,An)
-
逻辑表达式
逻辑表达式是由逻辑变量、逻辑运算符和必要的括号所构成的式子:
F = f ( A , B ) = A ˉ ⋅ B + A ⋅ B F=f(\mathrm{A,B})=\mathrm{\bar{A}\cdot B+A\cdot B} F=f(A,B)=Aˉ⋅B+A⋅B -
真值表
A B C F 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 0 1 1 1 0 \begin{array}{lll|l} \hline \mathrm{A} & \mathrm{B} & \mathrm{C} & \mathrm{F} \\ \hline 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ \hline \end{array} A00001111B00110011C01010101F01011100 -
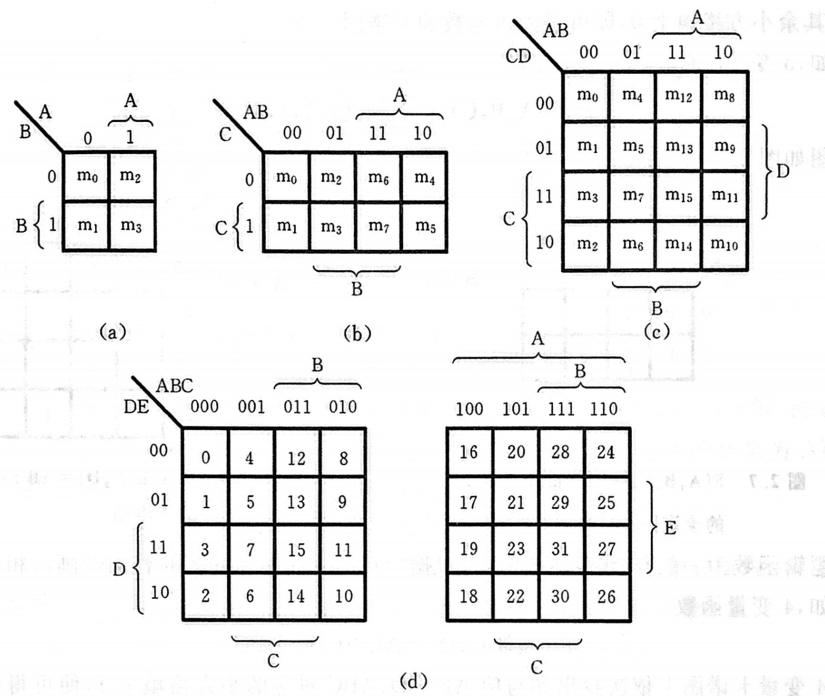
卡诺图
卡诺图是一种平面方格图, n n n 个变量的卡诺图由 2 n 2^n 2n 个小方格构成,单元格对应的最小项按格雷码摆放
逻辑代数的基本定理和规则
- 定理 1(0-1律): 0 + 0 = 0 1 + 0 = 1 0+0=0\quad 1+0=1 0+0=01+0=1 (其他同理。。。)
- 定理 2(重叠律): A + A = A A ⋅ A = A \mathrm{A+A=A\quad\quad A\cdot A=A} A+A=AA⋅A=A
- 定理 3(吸收律): A + A ⋅ B = A A ⋅ ( A + B ) = A \mathrm{A+A\cdot B=A\quad\quad A\cdot (A+B)=A} A+A⋅B=AA⋅(A+B)=A
- 定理 4(消除律): A + A ˉ ⋅ B = A + B A ⋅ ( A ˉ + B ) = A ⋅ B \mathrm{A+\bar{A}\cdot B=A+B\quad\quad A\cdot (\bar{A}+B)=A\cdot B} A+Aˉ⋅B=A+BA⋅(Aˉ+B)=A⋅B
- 定理 5(对合律): A ˉ ˉ = A \mathrm{\bar{\bar{A}}=A} Aˉˉ=A
- 定理 6(互补律): A + B ‾ = A ˉ ⋅ B ˉ A ⋅ B ‾ = A ˉ + B ˉ \mathrm{\overline{A+B}=\bar{A} \cdot \bar{B} \quad\quad \overline{A \cdot B}=\bar{A}+\bar{B}} A+B=Aˉ⋅BˉA⋅B=Aˉ+Bˉ
- 定理 7(并项律): A ⋅ B + A ⋅ B ˉ = A ( A + B ) ⋅ ( A + B ˉ ) = A \mathrm{A\cdot B +A\cdot \bar{B} =A \quad \quad (A+B)\cdot(A+\bar{B})=A} A⋅B+A⋅Bˉ=A(A+B)⋅(A+Bˉ)=A
- 定理 8(包含律): A ⋅ B + A ˉ ⋅ C + B ⋅ C = A ⋅ B + A ˉ ⋅ C \mathrm{A\cdot B+\bar{A}\cdot C+B\cdot C =A\cdot B+\bar{A}\cdot C } A⋅B+Aˉ⋅C+B⋅C=A⋅B+Aˉ⋅C
代入规则
任何一个代入含有变量 A \mathrm{A} A 的逻辑等式,如果将所有出现 A \mathrm{A} A 的位置都用同一个逻辑函数 F \mathrm{F} F 替代,等式仍然成立:
例如:给定逻辑等式 A ( B + C ) = A B + A C \mathrm{A(B+C)=AB+AC} A(B+C)=AB+AC 将 C \mathrm{C} C 都用 $\mathrm{C+D} 代替,得到 代替,得到 代替,得到\mathrm{A[B+(C+D)]=AB+A(C+D)}$ 仍然成立
反演规则
若将逻辑函数表达式
F
F
F 中所有的 “
⋅
\cdot
⋅”变成 “+”,“+”变成 “
⋅
\cdot
⋅”,“0”变成 “1”,“1”变成 “ 0 ”,原变量变成反变量,反变量变成原变量,并保持原函数中的运算顺序不变,则所得到的新的函数
F
‾
\overline{\mathrm{F}}
F 为原函数
F
\mathrm{F}
F 的反函数。
F
=
A
‾
⋅
B
+
C
⋅
D
‾
F
‾
=
(
A
+
B
‾
)
⋅
(
C
‾
+
D
)
\mathrm{F}=\overline{\mathrm{A}} \cdot \mathrm{B}+\mathrm{C} \cdot \overline{\mathrm{D}}\\\overline{\mathrm{F}}=(\mathrm{A}+\overline{\mathrm{B}}) \cdot(\overline{\mathrm{C}}+\mathrm{D})
F=A⋅B+C⋅DF=(A+B)⋅(C+D)
对偶规则
如果将逻辑函数表达式
F
\mathrm{F}
F 中所有的“
⋅
\cdot
⋅"变成“+”,“+”变 “
⋅
\cdot
⋅”, “0”变成“1”, “1”变成“0”, 并保持原函数中的运算顺序不变, 则所得到的新的逻辑表达式称为函数
F
\mathrm{F}
F 的对偶式, 并记作
F
′
\mathrm{ F^\prime}
F′
F
=
A
B
+
B
‾
(
C
+
0
)
F
′
=
(
A
+
B
)
(
B
‾
+
C
⋅
1
)
\mathrm{F}=\mathrm{A} \mathrm{B}+\overline{\mathrm{B}}(\mathrm{C}+\mathrm{0}) \quad \\ \quad \mathrm{F}^{\prime}=(\mathrm{A}+\mathrm{B})(\overline{\mathrm{B}}+\mathrm{C} \cdot \mathrm{1})
F=AB+B(C+0)F′=(A+B)(B+C⋅1)
复合逻辑
用两种及以上的逻辑复合而成的叫做复合逻辑,可以分为以下几类。
-
与非逻辑
F = A ⋅ B ⋅ C ⋯ ‾ \mathrm{F}=\overline{\mathrm{A} \cdot \mathrm{B} \cdot \mathrm{C} \cdots} F=A⋅B⋅C⋯
使用与非门可以实现与、或、非三种基本运算:与: F = A ⋅ B ‾ ⋅ 1 ‾ = A ⋅ B ‾ ‾ = A ⋅ B \mathrm{F}=\overline{\overline{\mathrm{A} \cdot \mathrm{B}} \cdot 1}=\overline{\overline{\mathrm{A} \cdot \mathrm{B}}}=\mathrm{A} \cdot \mathrm{B} F=A⋅B⋅1=A⋅B=A⋅B
或: F = A ⋅ 1 ‾ ⋅ B ⋅ 1 ‾ ‾ = A ‾ ⋅ B ‾ ‾ = A + B F=\overline{\overline{\mathrm{A} \cdot 1} \cdot \overline{\mathrm{B} \cdot 1}}=\overline{\overline{\mathrm{A}} \cdot \overline{\mathrm{B}}}=\mathrm{A}+\mathrm{B} F=A⋅1⋅B⋅1=A⋅B=A+B
非: F = A ⋅ 1 ‾ = A ‾ \mathrm{F}=\overline{\mathrm{A} \cdot \mathrm{1}}=\overline{\mathrm{A}} F=A⋅1=A
-
或非逻辑
F = A + B + C + ⋯ ‾ \mathrm{F}=\overline{\mathrm{A}+\mathrm{B}+\mathrm{C}+\cdots} F=A+B+C+⋯
使用或非门可以实现与、或、非三种基本运算:与: F = A + 0 ‾ + B + 0 ‾ ‾ = A ‾ + B ‾ ‾ = A ⋅ B \mathrm{F}=\overline{\overline{\mathrm{A}+0}+\overline{\mathrm{B}+0}}=\overline{\overline{\mathrm{A}}+\overline{\mathrm{B}}}=\mathrm{A} \cdot \mathrm{B} F=A+0+B+0=A+B=A⋅B
或: F = A + B ‾ + 0 ‾ = A + B ‾ ‾ = A + B F=\overline{\overline{A+B}+0}=\overline{\overline{A+B}}=\mathrm{A}+\mathrm{B} F=A+B+0=A+B=A+B
非: F = A + 0 ‾ = A ‾ \mathrm{F}=\overline{\mathrm{A}+0}=\overline{\mathrm{A}} F=A+0=A
-
与或非逻辑
F = A B + C D + ⋯ ‾ \mathrm{F}=\overline{\mathrm{AB}+\mathrm{CD}+\cdots} F=AB+CD+⋯ -
异或逻辑
F = A ⊕ B = A ‾ B + A B ‾ \mathrm{F}=\mathrm{A} \oplus \mathrm{B}=\overline{\mathrm{A}} \mathrm{B}+\mathrm{A} \overline{\mathrm{B}} F=A⊕B=AB+AB -
同或逻辑
F = A ⊙ B = A ‾ ⋅ B ‾ + A B \mathrm{F}=\mathrm{A} \odot \mathrm{B}=\overline{\mathrm{A}} \cdot \overline{\mathrm{B}}+\mathrm{AB} F=A⊙B=A⋅B+AB
代数化简法
代数化简法就是运用逻辑代数的公理、定理和规则对逻辑函数进行化简的方法。
以下是常用方法:
- 并项律:利用定理7中的 A B ‾ + A B = A \mathrm{A} \overline{\mathrm{B}}+\mathrm{AB}=\mathrm{A} AB+AB=A 消去多余变量
- 吸收律:利用定理3中的 A + A B = A \mathrm{A+AB=A} A+AB=A 吸收多余变量
- 消去律:利用定理4中的 A + A ˉ B = A + B A+\bar{A} B=A+B A+AˉB=A+B 消去多余变量
- 转换法:利用定理6中的 A + B ‾ = A ˉ ⋅ B ˉ A ⋅ B ‾ = A ˉ + B ˉ \overline{A+B}=\bar{A} \cdot \bar{B} \quad\quad \overline{A \cdot B}=\bar{A}+\bar{B} A+B=Aˉ⋅BˉA⋅B=Aˉ+Bˉ 转换变量
【例】化简
F
=
B
C
+
D
+
D
ˉ
⋅
(
B
ˉ
+
C
ˉ
)
⋅
(
A
D
+
B
C
ˉ
)
F=B C+D+\bar{D} \cdot(\bar{B}+\bar{C}) \cdot(A D+B \bar{C})
F=BC+D+Dˉ⋅(Bˉ+Cˉ)⋅(AD+BCˉ)
【解】
F
=
B
C
+
D
+
D
ˉ
⋅
(
B
ˉ
+
C
ˉ
)
⋅
(
A
D
+
B
C
ˉ
)
=
B
C
+
D
+
(
B
ˉ
+
C
ˉ
)
⋅
(
A
D
+
B
C
ˉ
)
[
消去律
]
=
B
C
+
D
+
B
C
‾
⋅
(
A
D
+
B
C
ˉ
)
[
互补律
]
=
B
C
+
D
+
A
D
+
B
C
ˉ
[
消去律
]
=
B
+
D
[
吸收律
,
并项律
]
\begin{aligned} F & =B C+D+\bar{D} \cdot(\bar{B}+\bar{C}) \cdot(A D+B \bar{C}) \\ & =B C+D+(\bar{B}+\bar{C}) \cdot(A D+B \bar{C}) [消去律]\\ & =B C+D+\overline{B C} \cdot(A D+B \bar{C})[互补律] \\ & =B C+D+A D+B \bar{C}[消去律] \\ & =B+D [吸收律 ,并项律] \end{aligned}
F=BC+D+Dˉ⋅(Bˉ+Cˉ)⋅(AD+BCˉ)=BC+D+(Bˉ+Cˉ)⋅(AD+BCˉ)[消去律]=BC+D+BC⋅(AD+BCˉ)[互补律]=BC+D+AD+BCˉ[消去律]=B+D[吸收律,并项律]
卡诺图化简法
要化简,首先我们要理解什么是 相邻
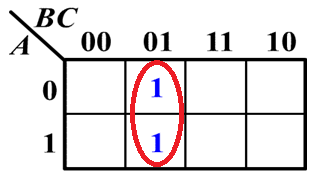
我们只考虑取值为1的格子(后简称1格子),从直观上看他们两就是相邻的,不仅如此,以下情况也算相邻
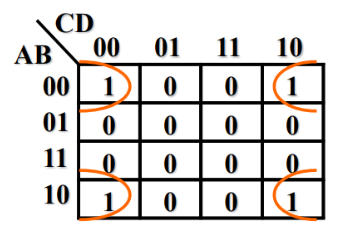
可能稍微有点难理解,这么远凭什么相邻呢?其实你可以把卡诺图看成卷筒纸中间那个纸筒,把他卷起来就相邻了
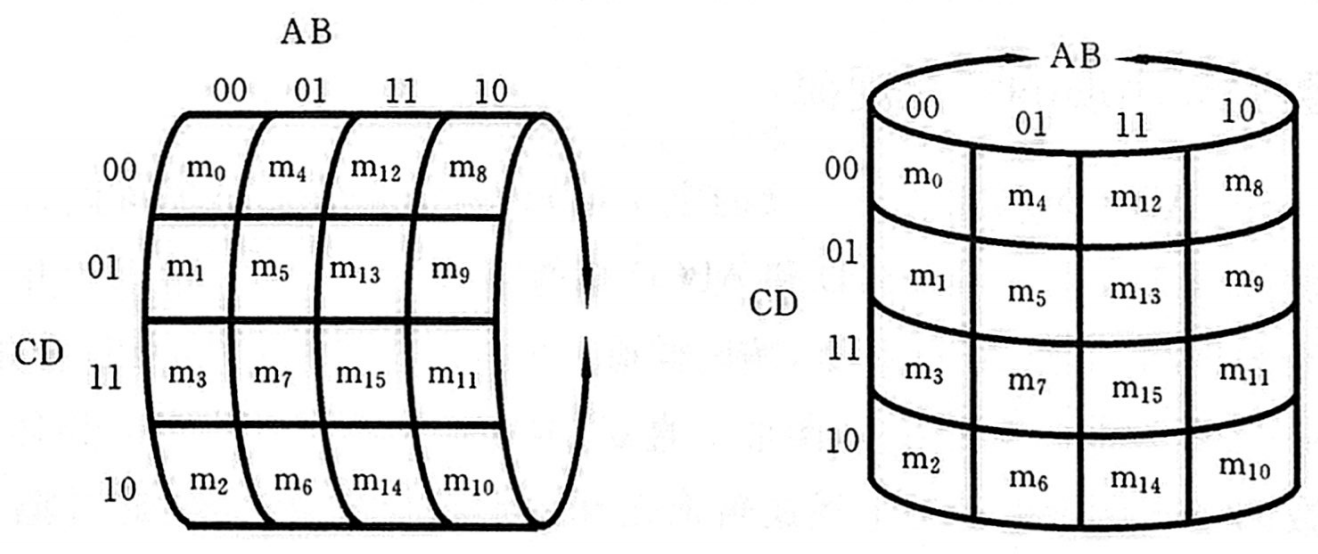
接着,你只需要理解一样东西:相邻的1格子可以合并。具体合并规则如下:
- 卡诺图中两个相邻1格的最小项可以合并成一个与项,并消去一个变量。
- 卡诺图中四个相邻1格的最小项可以合并成一个与项,并消去两个变量。
- 卡诺图中八个相邻1格的最小项可以合并成一个与项,并消去三个变量。
具体消去哪个变量,要看相邻格子之间是哪个变量在发生变化,消去变化的,留下不变的。
同时,我们还要保持以下原则:
- 将卡诺图中的1格画圈,一个也不能漏圈,否则最后得到的表达式就会与所给函数不等
- 1格允许被一个以上的圈所包围。
- 圈的个数应尽可能得少。即在保证1格一个也不漏圈的前提下,圈的个数越少越好。因为一个圈和一个与项相对应,圈数越少,与或表达式的与项就越少。
- 按照2k个方格来组合(即圈内的1格数必须为1,2,4,8等),圈的面积越大越好。因为圈越大,可消去的变量就越多,与项中的变量就越少。
- 每个圈应至少包含一个新的1格,否则这个圈是多余的。
- 用卡诺图化简所得到的最简与或式不是唯一的。
话不多说,让我们见一道例题。
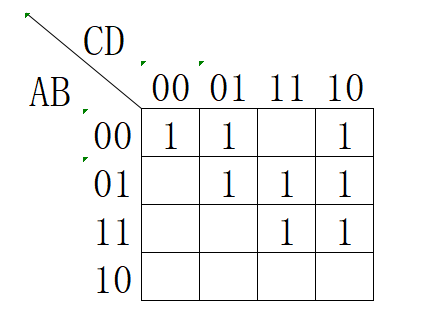
使用下面的方式画圈是不正确的,因为画多了
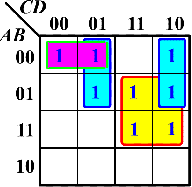
因此采取下列画圈方法:
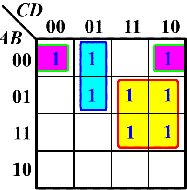
对于紫色圈:
A
ˉ
B
ˉ
C
ˉ
D
ˉ
+
A
ˉ
B
ˉ
C
D
ˉ
=
A
ˉ
B
ˉ
D
ˉ
\mathrm{\bar{A}\bar{B}\bar{C}\bar{D}+\bar{A}\bar{B}{C}\bar{D}=\bar{A}\bar{B}\bar{D}}
AˉBˉCˉDˉ+AˉBˉCDˉ=AˉBˉDˉ 发现了吗?
C
\mathrm{C}
C 正是圈中唯一变的量,因此可以消去,类似的,我们可以得到该卡诺图的最简与或式
F
=
B
C
+
A
ˉ
C
ˉ
D
+
A
ˉ
B
ˉ
D
ˉ
\mathrm{F=B C+\bar{A} \bar{C} D+\bar{A} \bar{B} \bar{D}}
F=BC+AˉCˉD+AˉBˉDˉ
第三章 集成门电路与触发器
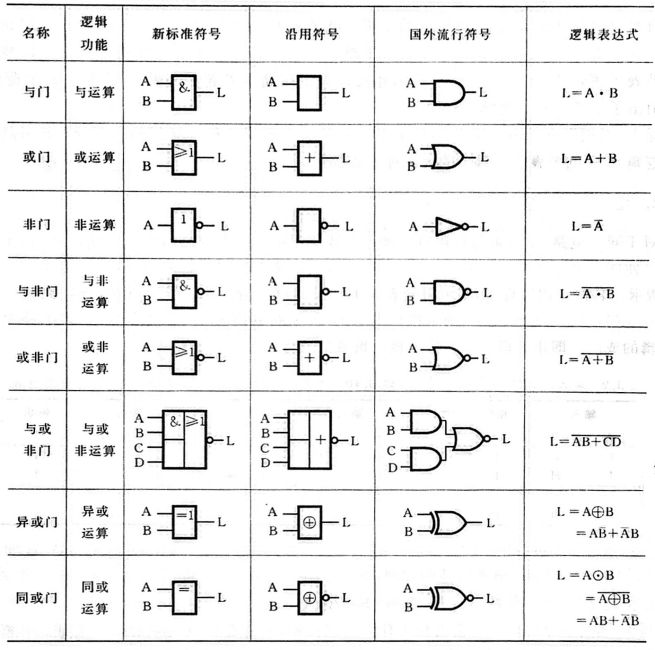
常用门电路符号及表达式
触发器
触发器是一种时序逻辑电路,是具有记忆功能的电路
- 时序逻辑电路的功能:任何时刻的稳定输出,不仅与 该时刻 的输入有关,还与电路 原状态 有关,即与以前的输入有关
触发器具有以下特点:
- 触发器有两个互补的输出端 Q \mathrm{Q} Q 和 Q ˉ \mathrm{\bar{Q}} Qˉ
- 触发器有两个稳定状态:
- 输出端 Q = 1 、 Q ˉ = 0 \mathrm{Q=1、\bar{Q}=0} Q=1、Qˉ=0 称为 “1”状态,表示逻辑1
- 输出端 Q = 0 、 Q ˉ = 1 \mathrm{Q=0、\bar{Q}=1} Q=0、Qˉ=1 称为 “0”状态,表示逻辑0
- 触发器的两个稳定状态可相互转换(称为状态的翻转)。通常把输入信号作用之前的状态称为“现态”,记作 Q n \mathrm{Q^n} Qn 和 Q ˉ n \mathrm{\bar{Q}^n} Qˉn ,把输入信号作用之后的状态称为“次态”,记作 Q n + 1 \mathrm{Q^{n+1}} Qn+1 和 Q ˉ n + 1 \mathrm{\bar{Q}^{n+1}} Qˉn+1
- 输入信号作用后,新状态可长期保持下来,电路具有记忆功能(能记忆 1 位二进制数的电路)
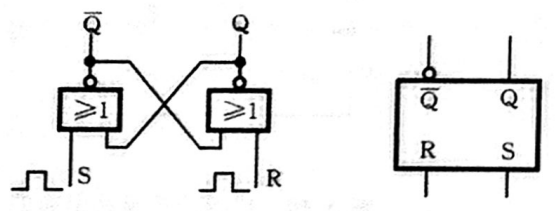
与非门构成基本 R-S 触发器
基本R-S触发器,又叫SR锁存器,是构成各种触发器的基本部件,也是最简单的一种触发器。
锁存器——不需要触发信号,由输入信号直接完成置 0 或置 1 操作。
触发器——需要一个触发信号 ,称为时钟信号 CLOCK ,只有触发信号有效时,才按输入信号完成置 0 或置 1 操作。
基本R-S触发器有两个输入端、两个输出端、两条反馈电路:
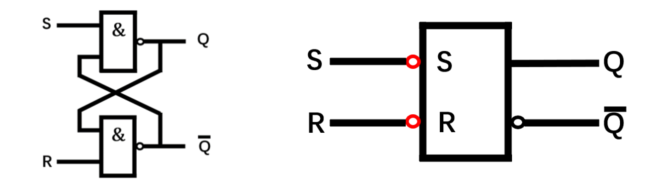
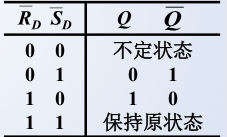
R-S触发器的状态:(输出 Q \mathrm{Q} Q 和 Q ‾ \mathrm{\overline Q} Q 互为相反逻辑,方便工作原理的分析)
- Q = 1 、 Q ˉ = 0 \mathrm{Q=1、\bar{Q}=0} Q=1、Qˉ=0 称为 “1”状态,表示逻辑1
- Q = 0 、 Q ˉ = 1 \mathrm{Q=0、\bar{Q}=1} Q=0、Qˉ=1 称为 “0”状态,表示逻辑0
工作原理
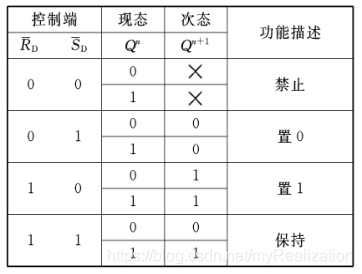
输入 R D ‾ = 0 , S D ‾ = 1 \overline{\mathrm{R}_{\mathrm{D}}}=0, \overline{\mathrm{S}_{\mathrm{D}}}=1 RD=0,SD=1 时,置 0 每次先从为 0 的输出端开始分析:
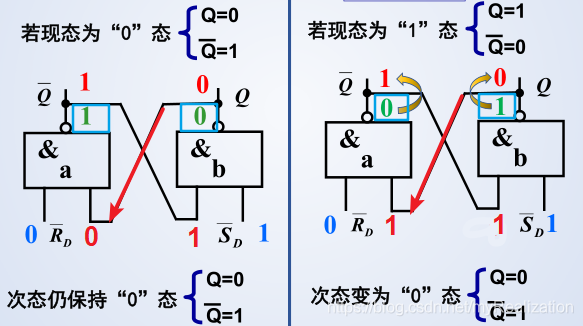
输入 R D ‾ = 1 , S D ‾ = 0 \overline{\mathrm{R}_{\mathrm{D}}}=1, \overline{\mathrm{S}_{\mathrm{D}}}=0 RD=1,SD=0 时,置 1
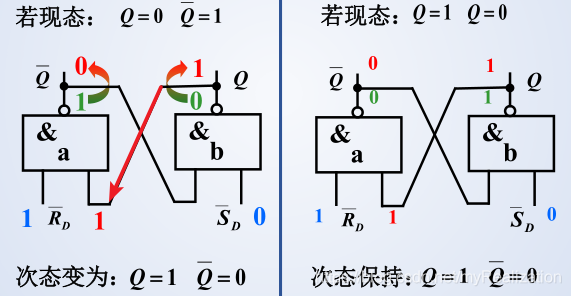
输入 R D ‾ = 1 , S D ‾ = 1 \overline{\mathrm{R}_{\mathrm{D}}}=1, \overline{\mathrm{S}_{\mathrm{D}}}=1 RD=1,SD=1 时,保持
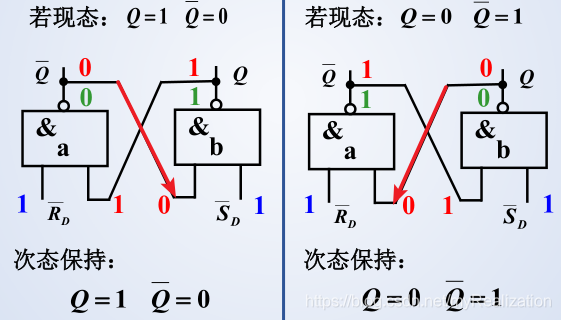
输入 R D ‾ = 0 , S D ‾ = 0 \overline{\mathrm{R}_{\mathrm{D}}}=0, \overline{\mathrm{S}_{\mathrm{D}}}=0 RD=0,SD=0 时,保持
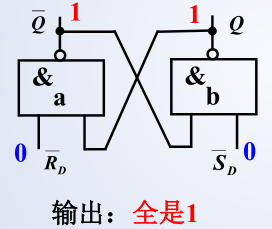
注意:当两个输入端由 0 变为 1时,翻转快的门输出变为 0 00 ,另一个不得翻转。因此,该状态为不定状态。
功能描述
状态转移真值表——反映触发器状态变化与输入之间的关系
次态方程
次态方程可以反映次态
Q
n
+
1
\mathrm{Q^{n+1}}
Qn+1 与现态、输入之间的关系,因为
R
,
S
\mathrm{R,S}
R,S 不允许同时为 0,可得:
Q
n
+
1
=
S
ˉ
+
R
⋅
Q
\mathrm{Q}^{\mathrm{n}+1} =\bar {\mathrm{S}}+\mathrm{R}\cdot \mathrm{Q}
Qn+1=Sˉ+R⋅Q
约束方程
因为
R
,
S
\mathrm{R,S}
R,S 不允许同时为 0,可得:
S
+
R
=
1
\mathrm{S}+\mathrm{R} =1
S+R=1
或非门构成基本 R-S 触发器
次态方程
Q n + 1 = S + R ‾ Q \begin{aligned} & \mathrm{Q}^{n+1}=\mathrm{S}+\overline{\mathrm{R}} \mathrm{Q} \\ \end{aligned} Qn+1=S+RQ
约束方程
R ⋅ S = 0 \mathrm{R} \cdot \mathrm{S}=0 R⋅S=0
钟控控制触发器
在数字系统中,为协调各部分的动作,常常要求某些触发器在 同一时刻 动作(即改变状态,也称为翻转)。这就要求有一个同步信号来控 制,这个控制信号叫做时钟脉冲信号( clock Pulse,CP),Clock Pulse 是一串周期性的矩形脉冲。
钟控 R-S 触发器
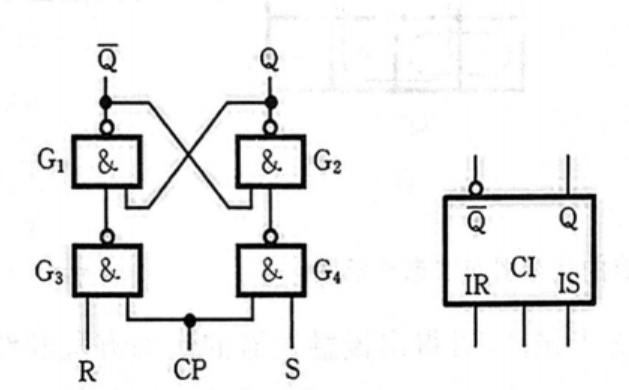
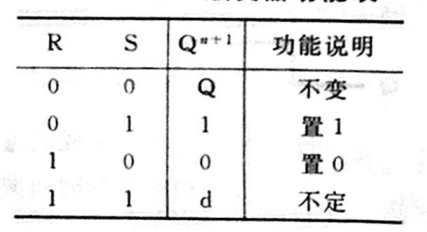
功能
R S Q n + 1 功能说明 0 0 Q 不变 0 1 1 置 1 1 0 0 置 0 1 1 d 不定 \begin{array}{cc|c|c} \hline \mathbf{R} & \mathbf{S} & \mathbf{Q}^{n+1} & \text { 功能说明 } \\ \hline 0 & 0 & \mathbf{Q} & \text { 不变 } \\ 0 & 1 & 1 & \text { 置 } 1 \\ 1 & 0 & 0 & \text { 置 } 0 \\ 1 & 1 & \mathrm{~d} & \text { 不定 } \\ \hline \end{array} R0011S0101Qn+1Q10 d 功能说明 不变 置 1 置 0 不定
看来R-S触发器是小黑子触发器,为什么呢,看后面就知道了🤣,R-S触发器功能的记忆技巧是:全零不变,全一未知,一正一负看S
次态方程
Q n + 1 = S + R ‾ Q n \begin{aligned} \mathrm{Q}^{\mathrm{n}+1} & =\mathrm{S}+\overline{\mathrm{R}} \mathrm{Q}^{\mathrm{n}} \\ \end{aligned} Qn+1=S+RQn
约束方程
R S = 0 \mathrm{RS} =0 RS=0
钟控D触发器
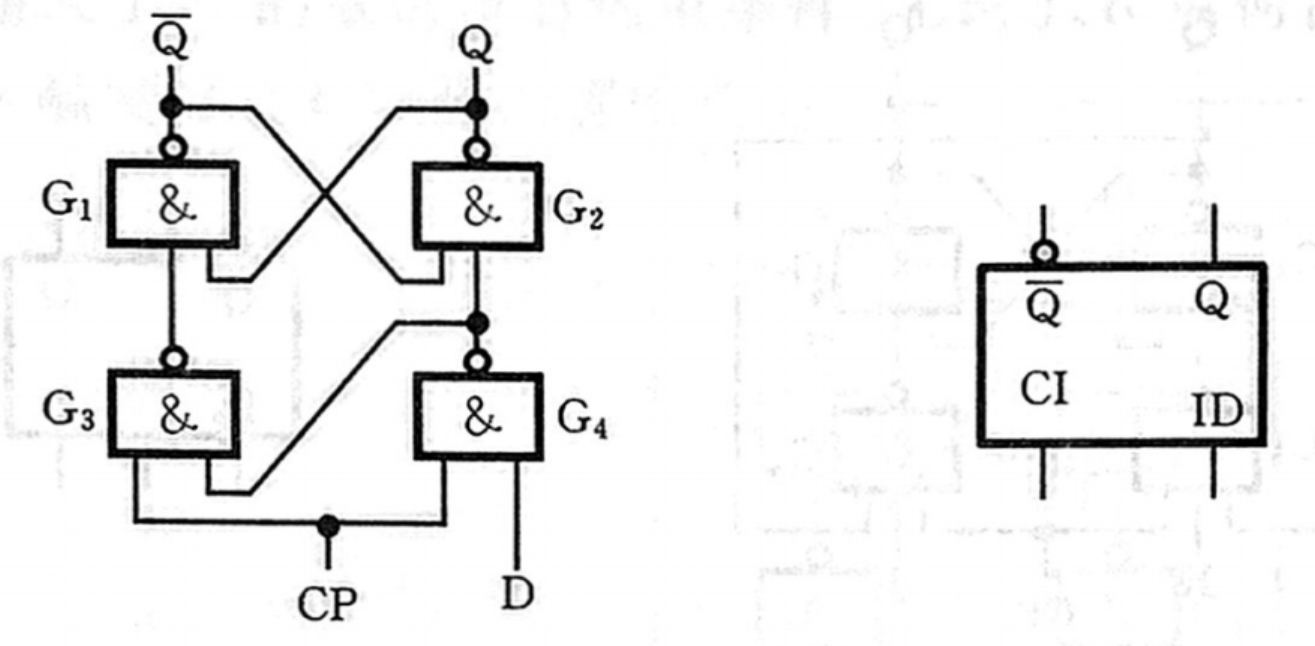
功能
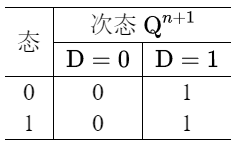
D Q n + 1 功 能 说 明 0 0 置 0 1 1 置 1 \begin{array}{c|c|c} \hline \mathrm{D} & \mathrm{Q}^{n+1} & \begin{array}{l} \text { 功 能 } \\ \text { 说 明 } \end{array} \\ \hline 0 & 0 & \text { 置 } 0 \\ 1 & 1 & \text { 置 } 1 \\ \hline \end{array} D01Qn+101 功 能 说 明 置 0 置 1
状态表
次态方程
Q n + 1 = D \mathrm{Q}^{n+1}=\mathrm{D} Qn+1=D
钟控 J-K 触发器
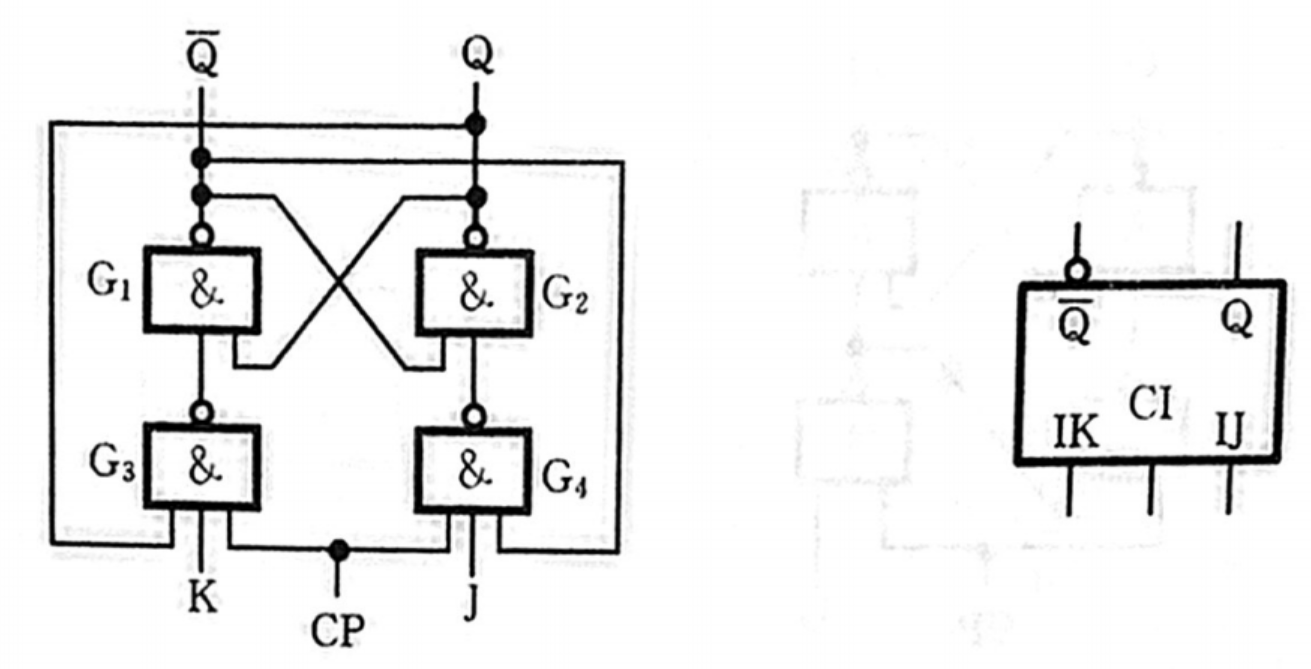
功能
在时钟信号(
C
P
\mathrm{CP}
CP) 为 0 时保持不变,在为 1 时有以下功能
J
K
Q
n
+
1
功能说明
0
0
Q
不变
0
1
0
置
0
1
0
1
置 1
1
1
Q
‾
翻转
\begin{array}{cc|c|c} \hline \mathrm{J} & \mathrm{K} & \mathrm{Q}^{n+1} & \text { 功能说明 } \\ \hline 0 & 0 & \mathrm{Q} & \text { 不变 } \\ 0 & 1 & 0 & \text { 置 } 0 \\ 1 & 0 & 1 & \text { 置 1 } \\ 1 & 1 & \overline{\mathrm{Q}} & \text { 翻转 } \\ \hline \end{array}
J0011K0101Qn+1Q01Q 功能说明 不变 置 0 置 1 翻转
对于这个功能,记忆技巧是“看 $\mathrm{J} $ 法 ”,全0不变,全1翻转,一正一负看
J
\mathrm{J}
J (
J
\mathrm{J}
J 是 1 那次态就是 1 ,
J
\mathrm{J}
J 是 0 那次态就是 0)
厉不厉害你鸡哥

状态表
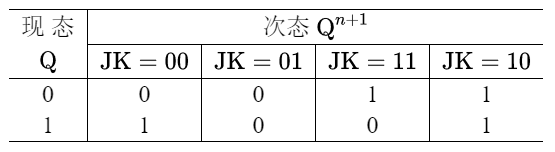
次态方程
Q n + 1 = J Q ˉ + K ˉ Q \mathrm{Q^{n+1}=J\bar{Q}+\bar{K}Q} Qn+1=JQˉ+KˉQ
钟控 T 触发器
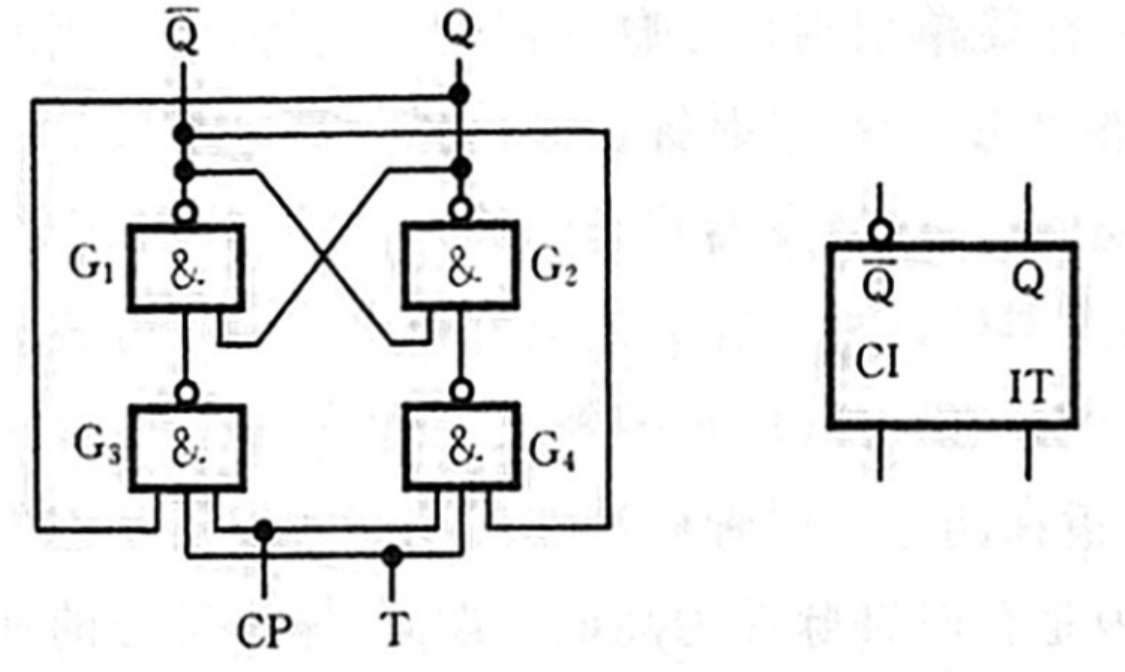
功能
T Q n + 1 功能说明 0 Q 不变 1 Q ˉ 翻转 \begin{array}{c|c|c} \hline \mathbf{T} & \mathbf{Q}^{n+1} & \text { 功能说明 } \\ \hline 0 & \mathrm{Q} & \text { 不变 } \\ 1 & \mathrm{\bar{Q}} & \text { 翻转 } \\ \hline \end{array} T01Qn+1QQˉ 功能说明 不变 翻转
次态方程
Q n + 1 = T Q ˉ + T ˉ Q = T ⊕ Q \mathrm{Q^{n+1}=T\bar{Q}+\bar{T}Q=T\oplus Q} Qn+1=TQˉ+TˉQ=T⊕Q
触发器的转换
R-S转D
将R输入接到S输入的输出上
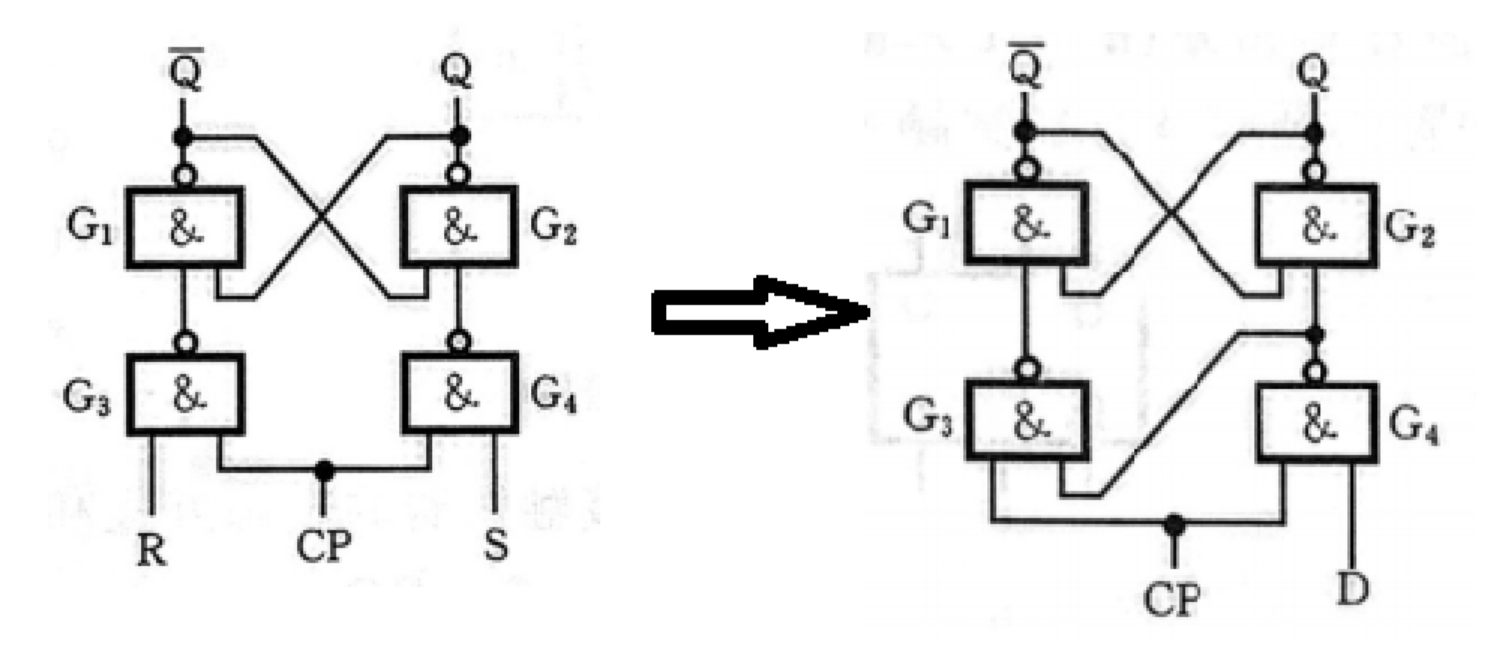
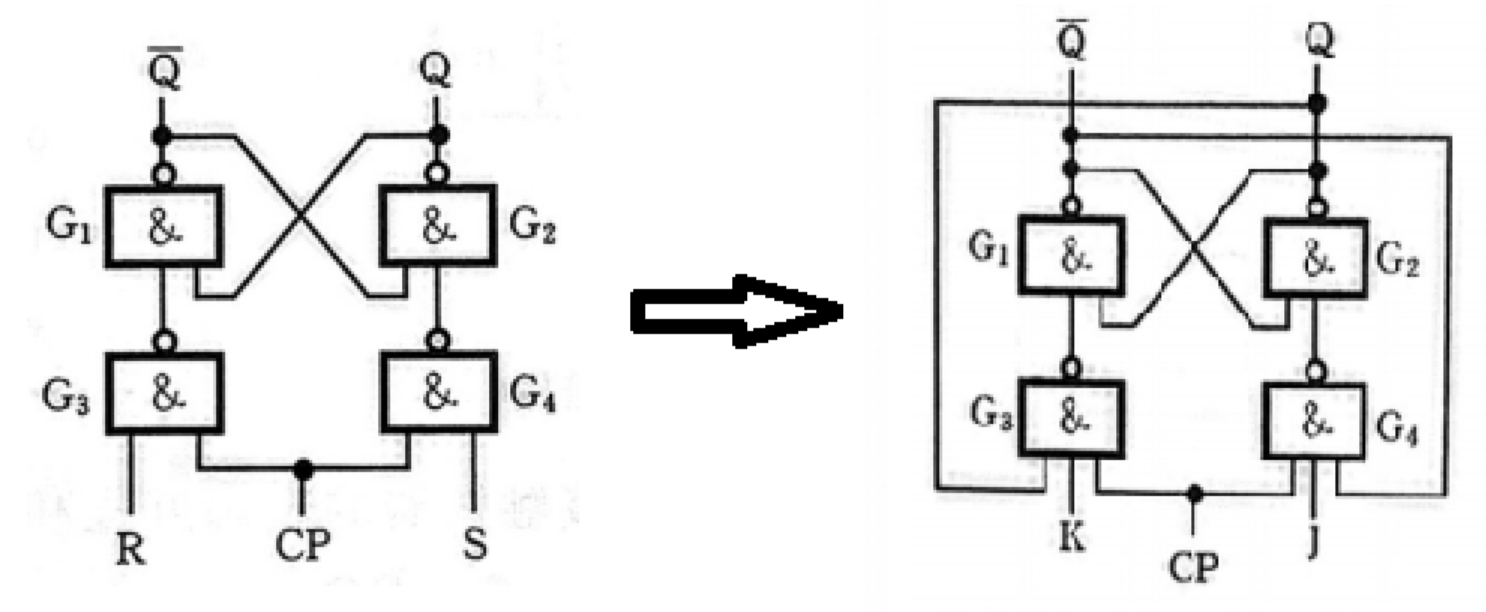
R-S转J-K
将输出的 Q \mathrm{Q} Q和 Q ˉ \mathrm{\bar{Q}} Qˉ 反接回输入端中
J-K转T
将两个输入 J \mathrm{J} J 和 K \mathrm{K} K 串起来变成一个输入
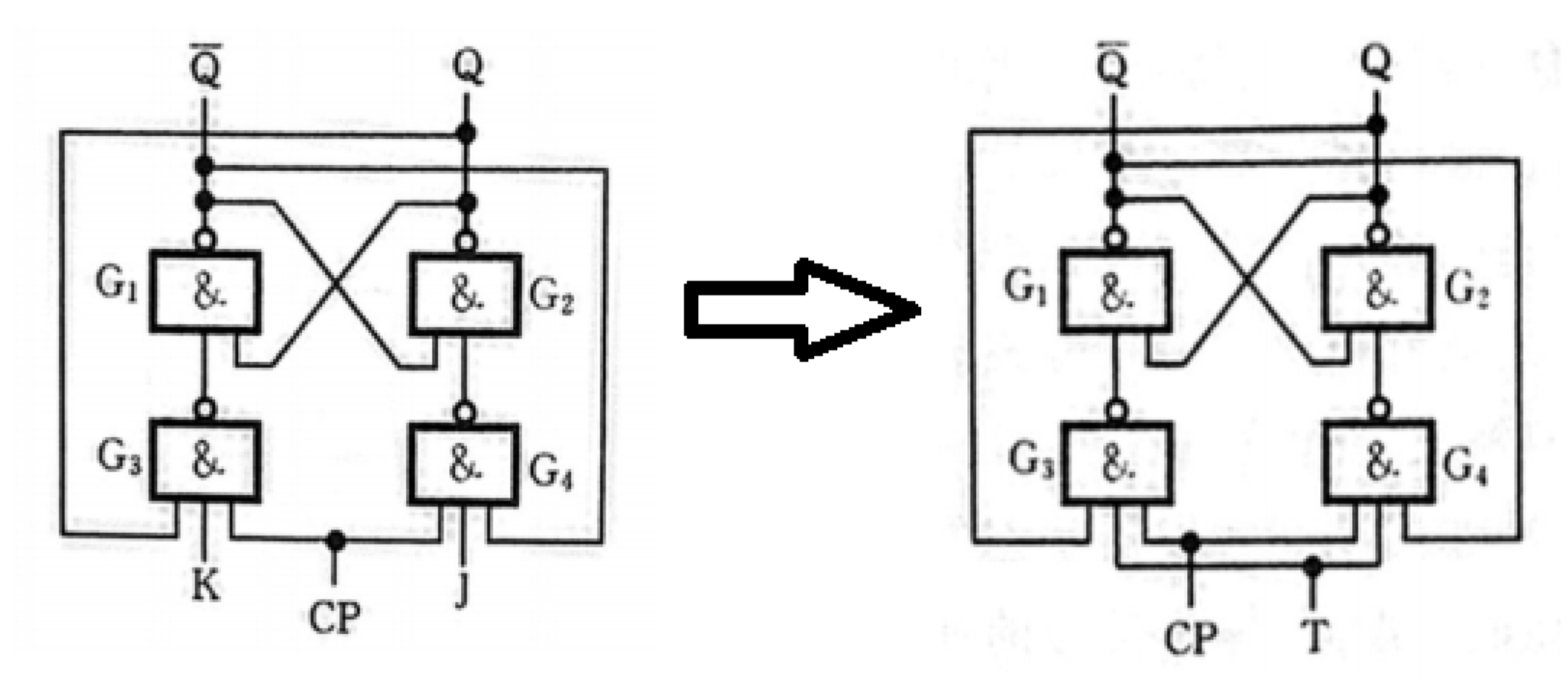
触发器的触发方式
- 在电路图标识中,如果一个触发器是边沿触发的,通常会有一个小三角形的符号在触发器的时钟输入端。这个三角形指的是边沿(上升或下降)触发。如果三角形后面还有一个小圆圈,那么这是下降(负)边沿触发;没有圆圈则是上升(正)边沿触发。
- 在数据表中,它会明确指出触发器的触发方式,包括它是否是边沿触发,以及是上升边沿触发还是下降边沿触发。





















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








