假设不带权有向图采用邻接矩阵G存储,设计实现以下功能的算法。
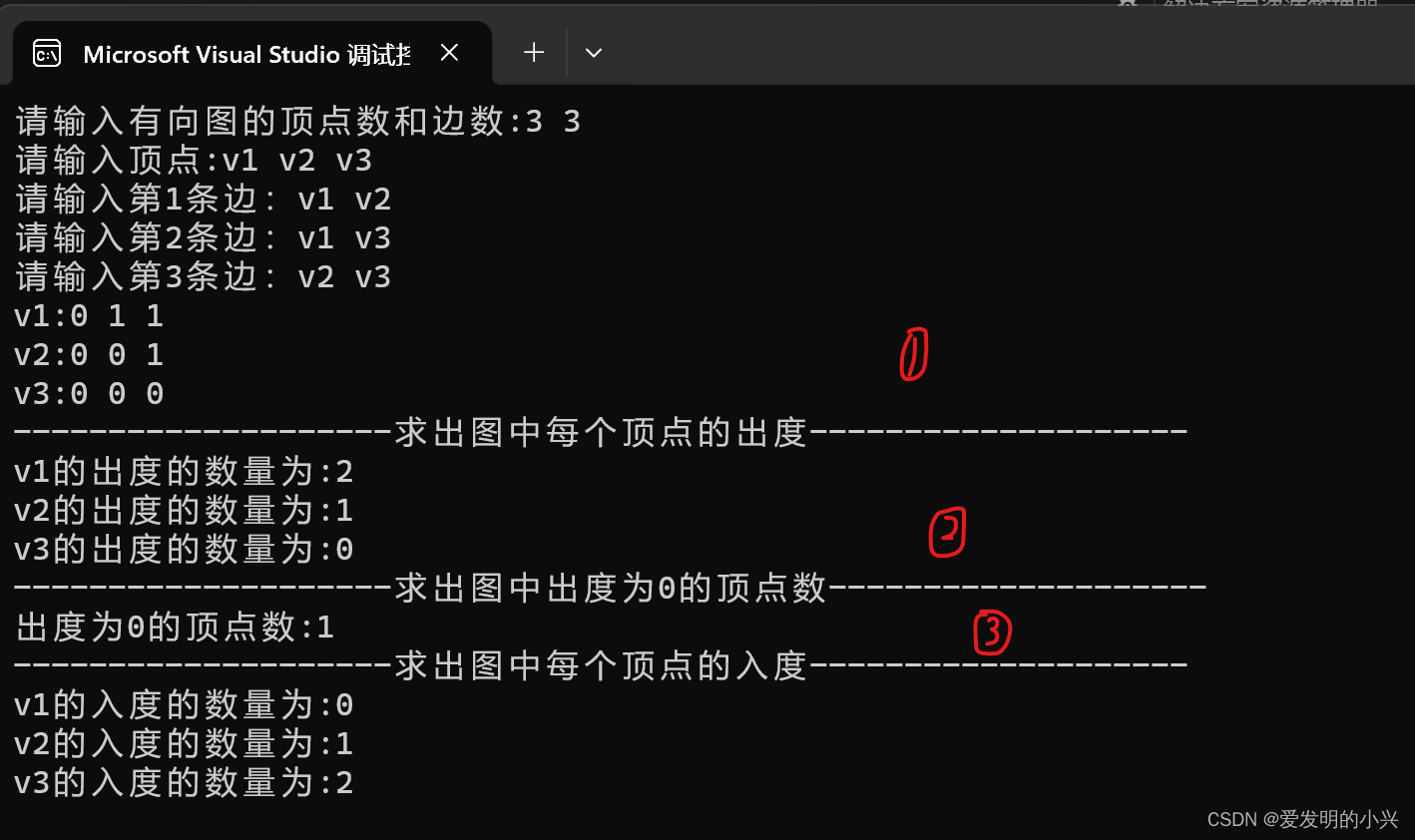
(1)求出图中每个顶点的出度。
(2)求出图中出度为0的顶点数。
(3)求出图中每个顶点的入度。
//参考博客:https://blog.csdn.net/qq_54162207/article/details/117414707
#include <iostream>
using namespace std;
#define Maxsize 100
#define VertexmMaxNum 20
#define ERROR 0
#define OK 1
typedef string VertexType;
typedef int EdgeType;
typedef struct Graph //无向图
{
VertexType vex[VertexmMaxNum];
EdgeType edge[VertexmMaxNum][VertexmMaxNum];
int vexnum; //顶点数
int edgenum; //边数
}Graph;
//确定某顶点在G中的位置下标
int locateVex(Graph& G, VertexType v)
{
for (int i = 0; i < G.vexnum; i++)
{
if (v == G.vex[i]) return i;
}
return -1;
}
void CreateDG(Graph& G)
{
int i = 0, j = 0;
cout << "请输入有向图的顶点数和边数:";
cin >> G.vexnum >> G.edgenum;
cout << "请输入顶点:";
for (i = 0; i < G.vexnum; i++)
{
cin >> G.vex[i];
}
for (i = 0; i < G.vexnum; i++)
{
for (j = 0; j < G.vexnum; j++)
G.edge[i][j] = 0;
}
for (int k = 0; k < G.edgenum; k++)
{
cout << "请输入第" << k + 1 << "条边:";
VertexType v1, v2;
cin >> v1 >> v2;
int i = locateVex(G, v1);
int j = locateVex(G, v2);
G.edge[i][j] = 1;
}
}
/*--------打印图的邻接矩阵-----------*/
void PrintfUGraph(Graph G) {
//将图的邻接矩阵输出在控制台上
for (int i = 0; i < G.vexnum; i++) {
cout << "v" << i + 1 << ":";
for (int j = 0; j < G.vexnum; j++)
cout << G.edge[i][j] << " ";
cout << endl;
}
}
//2.假设不带权有向图采用邻接矩阵G存储,设计实现以下功能的算法。
//(1)求出图中每个顶点的出度。
//(2)求出图中出度为0的顶点数。
//(3)求出图中每个顶点的入度。
//-------------------------核心代码-------------------------//
void count_chudu(Graph G)
{
int count = 0;
for (int i = 0; i < G.vexnum; i++)
{
count = 0;
for (int j = 0; j < G.vexnum; j++)
{
if (G.edge[i][j] == 1)
count++;
}
cout << G.vex[i] << "的出度的数量为:" << count << endl;
}
}
void count_chudu_zero(Graph G)
{
int zero_count = 0;
int count = 0;
for (int i = 0; i < G.vexnum; i++)
{
zero_count = 0;
for (int j = 0; j < G.vexnum; j++)
{
if (G.edge[i][j] == 0)
zero_count++;
}
if (zero_count == G.vexnum)
count++;
}
cout <<"出度为0的顶点数:" << count << endl;
}
void count_rudu(Graph G)
{
int count = 0;
for (int i = 0; i < G.vexnum; i++)
{
count = 0;
for (int j = 0; j < G.vexnum; j++)
{
if (G.edge[j][i] == 1)
count++;
}
cout << G.vex[i] << "的入度的数量为:" << count << endl;
}
}
//-------------------------核心代码-------------------------//
//顶点信息
//v1 v2 v3
//边信息
/*
v1 v2
v1 v3
v2 v3
*/
int main(void)
{
Graph G;
CreateDG(G); //不带权有向图
PrintfUGraph(G);
cout << "--------------------求出图中每个顶点的出度--------------------" << endl;
count_chudu(G);
cout << "--------------------求出图中出度为0的顶点数--------------------" << endl;
count_chudu_zero(G);
cout << "--------------------求出图中每个顶点的入度--------------------" << endl;
count_rudu(G);
return 0;
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








