最小方差无偏估计 MVUE
文章目录
1. 统计信号处理概述
统计信号处理就是把统计方法与手段应用在信号处理中的科学
通过采样获得的信号,对信号进行处理,获得信号的结构、关键参数、性质等信息。
2. 信号处理举例
2.1 问题描述
假设我们有一个直流分量A,我们对其进行采样,希望获得A的准确值。假设每一次得到的采样值都是独立同分布的。
对于这个问题,我们应该知道,采样值Z与A很大程度上是不一样的,因为存在噪声,也就是
Z = A + N , N i s n o i s e Z = A +N,N \quad is \quad noise Z=A+N,Nisnoise
2.2 处理方法
通常噪声是随机变量,也就是采样值Z也是随机变量。那么我们如何获得准确的A呢?
显然,如果就采样一次,直接使用,结果是完全不可控的
一般来说,我们可以采用的方法就是多次测量取平均,比如采样两次取平均,这样可以使得不确定的噪声的影响减少。
Z 1 , Z 2 = > 1 2 ( Z 1 + Z 2 ) Z1,Z2 => \frac{1}{2}(Z_1+Z2) Z1,Z2=>21(Z1+Z2)
2.3 处理原理
2.3.1 系统建模
上面的加权平均的方法就是一种信号处理。可是为什么这么操作能够使得结果更加准确呢?
下面我们建立一个研究模型进行讨论。
假设噪声N满足正态分布 N~N(0,σ2)
E
(
N
)
=
0
V
a
r
(
N
)
=
σ
2
E(N) = 0 \\ Var(N) = \sigma ^2
E(N)=0Var(N)=σ2
并且每次采样都是独立的,并且有
Z
=
A
+
N
,
N
i
s
n
o
i
s
e
Z
∼
N
(
A
,
σ
2
)
Z = A +N,N \quad is \quad noise \\ Z \sim N(A,\sigma ^2)
Z=A+N,NisnoiseZ∼N(A,σ2)
定义两次采样
Z 1 = A + N 1 Z 2 = A + N 2 Z_1 = A +N_1 \\ Z_2 = A +N_2 Z1=A+N1Z2=A+N2
定义两个变量
A ^ 1 = Z 1 A ^ 2 = Z 1 + Z 2 2 \hat A_1 = Z_1 \\ \hat A_2 = \frac{Z_1+Z_2}{2} A^1=Z1A^2=2Z1+Z2
2.3.2 处理分析
2.3.2.1 方差
在这个模型中,A是一个确定性的常数,N是一个随机变量,因此Z也是一个随机变量,如果我们减少噪声对系统的影响,其实也就是降低估计结果的方差。
因此我们仅仅需要验证加权平均是否能够减少系统方差
第一个随机变量的方差
V
a
r
(
A
^
1
)
=
V
a
r
(
Z
1
)
=
V
a
r
(
N
1
)
=
σ
2
Var(\hat A_1) = Var(Z_1) = Var(N_1) = \sigma ^2
Var(A^1)=Var(Z1)=Var(N1)=σ2
第二个随机变量的方差
V a r ( A ^ 2 ) = E [ ( A ^ 2 − E ( A ^ 2 ) ) 2 ] = E [ ( Z 1 + Z 2 2 − A ) 2 ] = 1 4 ∗ E [ ( Z 1 + Z 2 − 2 A ) 2 ] = 1 4 [ E ( Z 1 − A ) 2 + E ( Z 2 − A ) 2 + 2 ∗ E ( Z 1 − A ) ( Z 2 − A ) ] Var(\hat A_2) = E[(\hat A_2-E(\hat A_2))^2] = E[ (\frac{Z_1+Z_2}{2}-A)^2] \\ = \frac{1}{4}*E[ (Z_1+Z_2-2A)^2] = \frac{1}{4}[E(Z_1-A)^2+E(Z_2-A)^2+2*E(Z_1-A)(Z_2-A)] Var(A^2)=E[(A^2−E(A^2))2]=E[(2Z1+Z2−A)2]=41∗E[(Z1+Z2−2A)2]=41[E(Z1−A)2+E(Z2−A)2+2∗E(Z1−A)(Z2−A)]
因为每一次采样都是独立的,所以第三项可以进行拆分
E
(
Z
1
−
A
)
(
Z
2
−
A
)
=
E
(
Z
1
−
A
)
∗
E
(
Z
2
−
A
)
=
E
(
N
1
)
∗
E
(
N
2
)
=
0
E(Z_1-A)(Z_2-A) = E(Z_1-A)*E(Z_2-A) = E(N_1)*E(N_2)=0
E(Z1−A)(Z2−A)=E(Z1−A)∗E(Z2−A)=E(N1)∗E(N2)=0
因为噪声均值是0,所以上式为0
原 式 = 1 4 ∗ E [ ( Z 1 + Z 2 − 2 A ) 2 ] = 1 4 [ E ( Z 1 − A ) 2 + E ( Z 2 − A ) 2 ] = 1 4 ∗ [ V a r ( Z 1 ) + V a r ( Z 2 ) ] = 1 2 ∗ σ 原式 = \frac{1}{4}*E[ (Z_1+Z_2-2A)^2] = \frac{1}{4}[E(Z_1-A)^2+E(Z_2-A)^2] \\ = \frac{1}{4}*[Var(Z_1)+Var(Z_2)] = \frac{1}{2}*\sigma 原式=41∗E[(Z1+Z2−2A)2]=41[E(Z1−A)2+E(Z2−A)2]=41∗[Var(Z1)+Var(Z2)]=21∗σ
所以可以得到,确实两次采样求平均值能够减少随机变量的方差
因此说明,我们每次做实验的时候,都要对设备进行清零,是为了防止两次实验之间不是独立的
2.3.2.2 均值
不过,光看方差,还不能准确评估处理方案,必须还对均值进行评估。方差减少只能说明抖动减少了,并不能说明数据更加准确了。我们更加希望数据在目标附近上下抖动

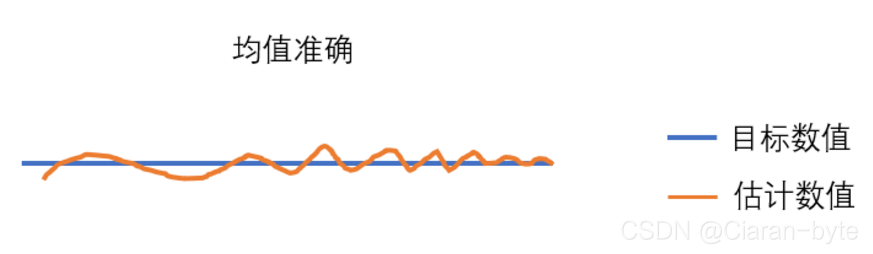
E ( A ^ 2 ) = E ( 1 2 ∗ ( Z 1 + Z 2 ) ) = 1 2 ( E ( Z 1 ) + E ( Z 2 ) ) = A E(\hat A_2) = E(\frac{1}{2}* (Z_1+Z_2) )\\ = \frac{1}{2}(E(Z_1)+E(Z_2) )= A E(A^2)=E(21∗(Z1+Z2))=21(E(Z1)+E(Z2))=A
可以看到,均值确实就是我们想要的。
2.3.3 更多次的加权平均
如果这样的话,是不是说明多做n次,数据方差就更小了呢?
随机变量的方差计算
A ^ n = 1 n ∗ ∑ k = 1 n Z k \hat A_n = \frac{1}{n}* \sum_{k=1}^{n}Z_k A^n=n1∗k=1∑nZk
V a r ( A ^ n ) = 1 n σ 2 Var(\hat A_n) = \frac{1}{n}\sigma ^2 Var(A^n)=n1σ2
随机变量的均值计算
E ( A ^ n ) = E ( 1 n ∗ ∑ k = 1 n Z k ) = 1 n ∗ ∑ k = 1 n E ( Z k ) = A E(\hat A_n) = E(\frac{1}{n}* \sum_{k=1}^{n}Z_k) \\ = \frac{1}{n}*\sum_{k=1}^{n}E(Z_k) = A E(A^n)=E(n1∗k=1∑nZk)=n1∗k=1∑nE(Zk)=A
可以看到多次进行加权平均确实能够起到很好的估计效果
但是用取平均的方法并不能说明他是最优的。我们下面要做的,就是为了评价我们使用的一个方法是不是好的,或者是不是最好的。如果不是最好的,最好的是否是存在的,如果最好的是存在的,我们如何找到他。
3. 信号处理方法的评估与优化
一般信号都是存在各种各样的分布模型的,而这些分布模型中有些参数是未知的。这里信号处理方法也可以理解为参数估计方法。就是利用我们采样获得的数据,用某种信号处理(参数估计)方法处理数据,然后计算分布模型中那些未知的参数。
但是我们并不知道得到的未知参数是否准确,这个时候就可以使用评估方法,评价用我们使用的方法进行参数估计是否准确。如果不准确,我们需要更换更好的信号处理方法。
因此我们在这里需要解决的问题是
- 如何判断一个处理方法是好的
- 判断处理方法是最优的标准是什么
- 如果处理方法是好的但不是最优的,怎么继续优化
- 信号处理方法可以优化到什么程度
3.1 如何判断一个处理方法是好的
3.1.1 参数化模型
要想对信号处理方法进行评估,我们首先要建立一个参数化模型 parametric model,也就是我们的采样的信号应该是服从某种分布的
Z
∼
f
(
x
,
θ
)
Z \sim f(x,\theta)
Z∼f(x,θ)
分布中有一些参数,应该具有这样的特点
- 确定的、没有随机性的
- 参数都是未知的
这些未知的参数,就是我们要进行估计的真值。而做信号处理的目的,就是为了对采样进行计算,对未知参数进行估计,然后让计算结果尽可能接近未知参数。
如在第2小节的例子中,A就是未知的参数。我们让该例子中的噪声为标准高斯噪声,那样的话采样的模型就变成了一种高斯分布。我们做信号处理就是为了确定这个A的大小
N ∼ N ( 0 , σ 2 ) Z ∼ N ( A , σ 2 ) N \sim N(0,\sigma ^2) \\ Z \sim N(A,\sigma ^2) N∼N(0,σ2)Z∼N(A,σ2)
这个就可以看做是小节2中信号处理问题的参数模型
3.1.2 损失函数
为了了解我们估计的参数是否是好的,我们需要有一个损失函数 loss functions
L
(
x
,
y
)
≥
0
,
L
∼
d
(
x
,
y
)
L(x,y) \geq 0, L \sim d(x,y)
L(x,y)≥0,L∼d(x,y)
损失函数是一个二元函数,一方面是大于等于0的,另一方面会随着两个变元距离的增大而增大
损失函数就是为了定义某种距离,当有了距离之后,就可以衡量一个估计是好还是不好,因为我们可以通过计算估计的参数和参数本身的距离来判断这种估计的损失了
L ( θ ^ , θ ) θ ^ = θ ^ ( Z ) L(\hat \theta,\theta) \\ \hat \theta = \hat \theta(Z) L(θ^,θ)θ^=θ^(Z)
其中\hat θ是参数的估计值,θ是参数的真值
对参数的估计就采样值的某种函数
3.1.3 小结
需要注意的是,这里的参数模型和损伤函数必须都是先验知识,也就是在我们采样实验之前就需要确定的。这种先验知识来源于不同的工程背景、个人的经验。对信号建模时往往屈从于自己能力的不足。就比如我们就喜欢吧噪声假定为高斯噪声,这是因为,在高斯之外,我们能做的事情就比较少了
3.2 信号处理的最优性
在学习了怎么判断一个参数估计方法是好的以后,我们下面需要了解判断一个信号处理方法是最优的条件是什么。
3.2.1 均方误差评估
首先要把损失函数定义出来
这里我们使用均方误差(MSE, Mean Square Error)作为损失函数
M S E = E [ ( θ ^ − θ ) 2 ] MSE = E[(\hat \theta-\theta)^2] MSE=E[(θ^−θ)2]
我们要找的最优的估计,就是在找均方误差最小的估计参数
m i n E [ ( θ ^ − θ ) 2 ] minE[(\hat \theta-\theta)^2] minE[(θ^−θ)2]
3.2.2 方差与偏差
下面我们均方误差评估进行变形,看看均方误差损失函数到底是怎么评价估计方法的
对均方误差进行变形,我们引入估计的期望。因为估计是采样的某种函数,所以估计值是个随机变量,因此估计的期望是存在的,也是可以计算的。
E [ ( θ ^ − θ ) 2 ] = E [ ( θ ^ − E ( θ ^ ) + E ( θ ^ ) − θ ) 2 ] E[(\hat \theta-\theta)^2] = E[(\hat \theta-E(\hat \theta)+E(\hat \theta)-\theta)^2] E[(θ^−θ)2]=E[(θ^−E(θ^)+E(θ^)−θ)2]
=
E
[
(
θ
^
−
E
(
θ
^
)
)
2
]
+
E
[
(
E
(
θ
^
)
−
θ
)
2
]
+
2
∗
E
[
(
θ
^
−
E
(
θ
^
)
)
∗
(
E
(
θ
^
)
−
θ
)
)
]
= E[(\hat \theta-E(\hat \theta))^2]+E[(E(\hat \theta)-\theta)^2]+2*E[(\hat \theta-E(\hat \theta))*(E(\hat \theta)-\theta))]
=E[(θ^−E(θ^))2]+E[(E(θ^)−θ)2]+2∗E[(θ^−E(θ^))∗(E(θ^)−θ))]
因为我们有确定的参数化模型,所以估计参数的均值E(\hat θ)是个常数,并且θ是个常数,因此第三项可以进行变形
E [ ( θ ^ − E ( θ ^ ) ) ∗ ( E ( θ ^ ) − θ ) ) ] = ( E ( θ ^ ) − θ ) ∗ E [ ( θ ^ − E ( θ ^ ) ) ] = ( u − θ ) ∗ E ( θ ^ − u ) = ( u − θ ) ∗ ( E ( θ ^ ) − u ) = 0 E[(\hat \theta-E(\hat \theta))*(E(\hat \theta)-\theta))] \\ =(E(\hat \theta)-\theta)*E[(\hat \theta-E(\hat \theta))] \\ = (u- \theta)*E(\hat \theta-u) \\ =(u- \theta)*(E(\hat \theta)-u) =0 E[(θ^−E(θ^))∗(E(θ^)−θ))]=(E(θ^)−θ)∗E[(θ^−E(θ^))]=(u−θ)∗E(θ^−u)=(u−θ)∗(E(θ^)−u)=0
那么原式就可以继续化简
E [ ( θ ^ − θ ) 2 ] = E [ ( θ ^ − E ( θ ^ ) ) 2 ] + E [ ( E ( θ ^ ) − θ ) 2 ] E[(\hat \theta-\theta)^2] =E[(\hat \theta-E(\hat \theta))^2]+E[(E(\hat \theta)-\theta)^2] E[(θ^−θ)2]=E[(θ^−E(θ^))2]+E[(E(θ^)−θ)2]
可以看出,前一项是随机变量方差的定义,后一项是随机变量偏差的定义(估计值与真值的差)
M S E = V a r i a n c e + B i a s MSE = Variance +Bias MSE=Variance+Bias
我们可以知道,均方误差实际上是通过评估系统的方差和偏差,而对信号处理方案进行评估的。
3.2.3 Variance Bias Tradeoff
我们势必要在bias和variance之间做出tradeoff。
一般来说我们更加希望variance更小,因为偏差代表的是系统误差,方差代表的是随机误差。系统误差是很容易用系统性方法进行校正的。
3.2.4 对均方误差估计的进一步探讨
这里我们举一个例子,这个例子是使用对参数取平均值的方法估计参数,然后我们使用均方误差对这种参数估计方法进行评价。
我们假设有这样一个无偏估计(没有偏差),我们做了n次采样,并且对n次采取取平均,我们计算一下这种对真值估计方法的均方误差
处理方法数学描述如下
U n b i a s : E ( θ ^ ) = θ Z 1 , . . . , Z n = > 1 n ∑ k = 1 n Z k = Z ˉ Unbias: E(\hat \theta) = \theta \\ Z_1,...,Z_n => \frac{1}{n}\sum_{k=1}^{n}Z_k = \bar Z Unbias:E(θ^)=θZ1,...,Zn=>n1k=1∑nZk=Zˉ
计算均方误差
E [ ( Z ˉ − θ ) 2 ] = V a r ( Z ˉ ) + E [ ( E ( Z ˉ ) − θ ) 2 ] E[(\bar Z-\theta)^2] = Var(\bar Z)+ E[(E(\bar Z)-\theta)^2] E[(Zˉ−θ)2]=Var(Zˉ)+E[(E(Zˉ)−θ)2]
因为估计是无偏的,所以后者为0
E [ ( Z ˉ − θ ) 2 ] = V a r ( Z ˉ ) = 1 n ∑ k = 1 n ( Z k − θ ) 2 E[(\bar Z-\theta)^2] = Var(\bar Z) = \frac{1}{n}\sum_{k=1}^{n}(Z_k-\theta)^2 E[(Zˉ−θ)2]=Var(Zˉ)=n1k=1∑n(Zk−θ)2
因此,我们实际上就是利用方差来估计,取均值的方法进行参数估计是否是可靠的。
但是,我们发现,均方误差是没有办法来评估这种估计方法的好坏的,因为我们不可能知道真值θ是多少,也就计算不出损失函数的数值。因此,我们往往会利用平均值来代替真值。但是这样前面的系数就会发生变化
E [ ( Z ˉ − θ ) 2 ] = V a r ( Z ˉ ) = 1 n − 1 ∑ k = 1 n ( Z k − Z ˉ ) 2 E[(\bar Z-\theta)^2] = Var(\bar Z) = \frac{1}{n-1}\sum_{k=1}^{n}(Z_k-\bar Z)^2 E[(Zˉ−θ)2]=Var(Zˉ)=n−11k=1∑n(Zk−Zˉ)2
我们来证明一下,为什么前面的参数会发生改变,其实是为了满足无偏估计。我们需要让损失函数改变前后的期望不变。
E [ 1 n − 1 ∑ k = 1 n ( Z k − Z ˉ ) 2 ] = V a r E[\frac{1}{n-1}\sum_{k=1}^{n}(Z_k-\bar Z)^2] = Var E[n−11k=1∑n(Zk−Zˉ)2]=Var
我们需要让用平均值替代了真值的项的均值也为方差,才能保证无偏估计
E [ ∑ k = 1 n ( Z k − Z ˉ ) 2 ] = E [ ∑ k = 1 n ( Z k 2 ) + n ∗ Z ˉ 2 − 2 ∗ ∑ k = 1 n ( Z k ) ∗ Z ˉ ] = E [ ∑ k = 1 n ( Z k 2 ) + n ∗ Z ˉ 2 − 2 ∗ n ∗ ( Z ˉ ) 2 ] = E [ ∑ k = 1 n ( Z k 2 ) − n ∗ Z ˉ 2 ] E[\sum_{k=1}^{n}(Z_k-\bar Z)^2] \\ = E[\sum_{k=1}^{n}(Z_k^2)+n*\bar Z^2 -2*\sum_{k=1}^{n}(Z_k)*\bar Z] \\ = E[\sum_{k=1}^{n}(Z_k^2)+n*\bar Z^2 -2*n*(\bar Z)^2] \\ =E[\sum_{k=1}^{n}(Z_k^2)-n*\bar Z^2 ] E[k=1∑n(Zk−Zˉ)2]=E[k=1∑n(Zk2)+n∗Zˉ2−2∗k=1∑n(Zk)∗Zˉ]=E[k=1∑n(Zk2)+n∗Zˉ2−2∗n∗(Zˉ)2]=E[k=1∑n(Zk2)−n∗Zˉ2]
因为
Z ˉ 2 = ( 1 n ∗ ∑ k = 1 n Z k ) 2 = 1 n 2 ∗ ( ∑ k = 1 n Z k 2 + ∑ i = j Z i Z j ) \bar {Z}^2 = (\frac{1}{n}*\sum_{k=1}^{n}Z_k)^2 \\ = \frac{1}{n^2}*(\sum_{k=1}^{n}Z_k^2+\sum_{i\cancel= j}Z_iZ_j) Zˉ2=(n1∗k=1∑nZk)2=n21∗(k=1∑nZk2+i= j∑ZiZj)
代入可得
E
[
∑
k
=
1
n
(
Z
k
−
Z
ˉ
)
2
]
=
E
[
∑
k
=
1
n
(
Z
k
2
)
−
1
n
∗
(
∑
k
=
1
n
Z
k
2
+
∑
i
=
j
Z
i
Z
j
)
]
E[\sum_{k=1}^{n}(Z_k-\bar Z)^2] \\ =E[\sum_{k=1}^{n}(Z_k^2)-\frac{1}{n}*(\sum_{k=1}^{n}Z_k^2+\sum_{i\cancel= j}Z_iZ_j) ]
E[k=1∑n(Zk−Zˉ)2]=E[k=1∑n(Zk2)−n1∗(k=1∑nZk2+i=
j∑ZiZj)]
因为所有的采样都是独立并且同分布,所以乘积可以分开
E [ ∑ k = 1 n ( Z k 2 ) − 1 n ∗ ( ∑ k = 1 n Z k 2 + ∑ i = j Z i Z j ) ] = ∑ k = 1 n E ( Z k 2 ) − 1 n ∑ k = 1 n E ( Z k 2 ) − 1 n ∑ i = j E ( Z i ) E ( Z j ) E[\sum_{k=1}^{n}(Z_k^2)-\frac{1}{n}*(\sum_{k=1}^{n}Z_k^2+\sum_{i\cancel= j}Z_iZ_j) ] \\ =\sum_{k=1}^{n}E(Z_k^2)-\frac{1}{n}\sum_{k=1}^{n}E(Z_k^2)-\frac{1}{n}\sum_{i\cancel= j}E(Z_i)E(Z_j) E[k=1∑n(Zk2)−n1∗(k=1∑nZk2+i= j∑ZiZj)]=k=1∑nE(Zk2)−n1k=1∑nE(Zk2)−n1i= j∑E(Zi)E(Zj)
因为每次采样都是同分布的,因此可以找一个变量Z1来替代所有的变量Zk
∑ k = 1 n E ( Z k 2 ) − 1 n ∑ k = 1 n E ( Z k 2 ) − 1 n ∑ i = j E ( Z i ) E ( Z j ) = ∑ k = 1 n E ( Z 1 2 ) − 1 n ∑ k = 1 n E ( Z 1 2 ) − 1 n ∑ i = j [ E ( Z 1 ) ] 2 = n ∗ E ( Z 1 2 ) − 1 n ∗ n ∗ E ( Z 1 2 ) − 1 n ∗ n ∗ ( n − 1 ) ∗ [ E ( Z 1 ) ] 2 = ( n − 1 ) [ E ( Z 1 2 ) − ( E ( Z 1 ) ) 2 ] = ( n − 1 ) ∗ V a r ( Z 1 ) \sum_{k=1}^{n}E(Z_k^2)-\frac{1}{n}\sum_{k=1}^{n}E(Z_k^2)-\frac{1}{n}\sum_{i\cancel= j}E(Z_i)E(Z_j) \\ = \sum_{k=1}^{n}E(Z_1^2)-\frac{1}{n}\sum_{k=1}^{n}E(Z_1^2)-\frac{1}{n}\sum_{i\cancel= j}[E(Z_1)]^2 \\ = n*E(Z_1^2)-\frac{1}{n}*n*E(Z_1^2)-\frac{1}{n}*n*(n-1)*[E(Z_1)]^2 \\ = (n-1)[E(Z_1^2)-(E(Z_1))^2] = (n-1)*Var(Z_1) k=1∑nE(Zk2)−n1k=1∑nE(Zk2)−n1i= j∑E(Zi)E(Zj)=k=1∑nE(Z12)−n1k=1∑nE(Z12)−n1i= j∑[E(Z1)]2=n∗E(Z12)−n1∗n∗E(Z12)−n1∗n∗(n−1)∗[E(Z1)]2=(n−1)[E(Z12)−(E(Z1))2]=(n−1)∗Var(Z1)
怕自己忘记,最后一步进行推导
V
a
r
(
Z
)
=
E
[
(
Z
−
E
(
Z
)
)
2
]
=
E
(
Z
2
+
[
E
(
Z
)
]
2
−
2
∗
Z
∗
E
(
Z
)
)
=
E
(
Z
2
)
+
[
E
(
Z
)
]
2
−
2
∗
E
(
Z
)
∗
E
(
Z
)
=
E
(
Z
2
)
−
[
E
(
Z
)
]
2
Var(Z) = E[(Z-E(Z))^2] \\ = E(Z^2+[E(Z)]^2-2*Z*E(Z)) \\ =E(Z^2) + [E(Z)]^2 - 2*E(Z)*E(Z) \\ = E(Z^2) - [E(Z)]^2
Var(Z)=E[(Z−E(Z))2]=E(Z2+[E(Z)]2−2∗Z∗E(Z))=E(Z2)+[E(Z)]2−2∗E(Z)∗E(Z)=E(Z2)−[E(Z)]2
因此,如果使用均值的话,必须除以n-1才行,得到的才是对方差的无偏估计
事实上,我们可以用另外一个角度考虑,其实如果用均值代表真值,自由度降低了1,所以除的就不是n,而是n-1
3.2.5 最小方差无偏估计的引入
3.2.5.1 信号处理的最优性探讨
信号处理的最优,就是希望能够极小化均方误差(MMSE,Minimum Mean Square Error)
3.2.5.2 信号处理方法的通用性探讨
其实,均方误差的产生,一方面与我们的估计值 \hat θ有关,另外一方法还可能与θ有关。
E [ ( θ ^ − θ ) 2 ] E[(\hat \theta- \theta)^2] E[(θ^−θ)2]
最优估计往往是依赖于θ的,我们希望找到更加通用的评估方法,就是对任意的θ都是最优的,但是这种东西理论上是不存在的。
就比如一个优秀的内科医生,往往看外科水平就比较低
3.2.5.3 信号处理方法的及格线
在选择信号处理方法的时候,其实是有及格线的。还是以行医为例,如果有些江湖大夫,给谁看病都说别人糖尿病,这样的话,总有概率能够碰上,一旦碰上了,估计就是最优的。这一种思路叫做只看一点,不看其余的方案。
比如我们定义一种评估方法
θ ^ = θ 0 \hat \theta = \theta_0 θ^=θ0
这种方法总有概率获得最好的估计值。但是这种评估方法显然是不靠谱的。
为了避免上面的情况,就需要有一种机制。比如为了防止江湖医生行骗,就要求医生上岗需要行医资格证。对应到信号处理中,就要求每一种估计都是无偏估计,这是一种合格线。也就是不需要证明一个人每个学科都是专家,但是至少证明每个学科都不是白痴。
即 E ( θ ^ ) = θ 即\quad\quad E(\hat \theta) = \theta 即E(θ^)=θ
3.2.5.4 MVUE 最小方差无偏估计
当我们引入无偏估计作为信号处理方法的及格线时,MSE在无偏的基础上,就变成了方差了。也叫做UMV(一致最小方差),因此这个时候我们评估一个处理方法好坏的时候,就只需要考虑方差了。这个时候的估计方法叫做MVUE minimum variance unbias estimator 最小方差无偏估计。这种估计的前提条件就是,我们使用的信号处理方法(估计方法)是无偏的。
3.3 基于MVUE标准的信号处理方法的优化
在理解信号处理方法的优化之前,我们需要准备一些预备知识。
3.3.1 预备知识
3.3.1.1 条件期望
先引入一个概念–条件期望 conditional expectation
(1) 条件期望的概念
条件期望E(Y|Z)的含义是:以Z为条件Y的期望
这里需要注意的是,条件期望是一个***随机变量***。
为什么是个随机变量呢?因为条件号左边的随机变量在求期望的过程中,随机性就消失了,但是条件号右边仍然是随机变量,并且没有随着期望的进行消失。
后面的随机变量是先验的、已知的。
(2) 条件期望的性质
我们先引入条件期望的性质。
- 性质一 :对条件期望的期望,就是对(Z,Y)无条件的期望
E ( E Z ( g ( Z , Y ) ∣ Y ) ) = E ( g ( Z , Y ) ) E(E_Z(g(Z,Y)|Y)) = E(g(Z,Y)) E(EZ(g(Z,Y)∣Y))=E(g(Z,Y))
- 性质二 :条件期望限定住的部分,可以进行拆分
E ( Z ∗ g ( Y ) ∣ Y ) = g ( Y ) ∗ E ( Z ∣ Y ) E(Z *g(Y)|Y) = g(Y)*E(Z|Y) E(Z∗g(Y)∣Y)=g(Y)∗E(Z∣Y)
这个可以这么理解,g(Y)在条件期望中是个常数,而常数是可以从期望里面拿到外面的
(3) 条件期望的用途
- 引入条件期望的原因
引入条件期望的原因,是有时候处理复杂随机现象的时候,可能有若干随机因素对系统产生影响,我们就假定一部分因素的随机性因素消失了,然后进行各个处理,等处理出来以后,再让其随机性暴露出来,再进行处理。
- n个随机变量求均值
这里举个例子进行说明
Z 1 , . . . , Z n E ( Z 1 + . . + Z n ) Z_1,...,Z_n \\ E(Z_1+..+Z_n) Z1,...,ZnE(Z1+..+Zn)
假设有一组独立同分布的随机变量,我们希望计算他们和的期望
E ( Z 1 + . . + Z n ) = n ∗ E ( Z 1 ) E(Z_1+..+Z_n) = n* E(Z_1) E(Z1+..+Zn)=n∗E(Z1)
- 随机个随机变量求均值
然后把问题稍微复杂化一点,仍然求n个变量和的均值,但是这里n的个数是随机的,因此记做N,因此就变成了随机个随机变量的值,仍然要计算期望
如果我们要延续刚才的计算
Z 1 , . . . , Z N E ( Z 1 + . . + Z N ) = N ∗ E ( Z 1 ) Z_1,...,Z_N \\ E(Z_1+..+Z_N) = N* E(Z_1) Z1,...,ZNE(Z1+..+ZN)=N∗E(Z1)
这样的话,结果就荒唐了,因为期望应该是个确定值,但是得到的结果是个随机变量
那正确结果是什么呢?我们可以来猜测一个
E ( Z 1 + . . + Z N ) = E ( N ) ∗ E ( Z 1 ) E(Z_1+..+Z_N) = E(N)* E(Z_1) E(Z1+..+ZN)=E(N)∗E(Z1)
事实上,这个答案是正确的,下面我们来证明一下
我们的困难在于,有两个随机因素。这个时候我们就要采用各个击破的思想,先条件住一部分,再处理另外一部分,然后再回来处理条件的部分。
条件住Y处理Z,这个时候Y就不具有随机性了,等处理完Z再处理Y的时候,Z就没有随机性了,就好处理了
E ( Z 1 + . . . + Z N ) = E ( E ( ∑ k = 1 n Z k ∣ N = n ) ) E(Z_1+...+Z_N) = E(E(\sum_{k=1}^{n}Z_k|N=n)) E(Z1+...+ZN)=E(E(k=1∑nZk∣N=n))
也可以写做下面的样子
E ( Z 1 + . . . + Z N ) = E ( E ( ∑ k = 1 N Z k ∣ N ) ) E(Z_1+...+Z_N) = E(E(\sum_{k=1}^{N}Z_k|N)) E(Z1+...+ZN)=E(E(k=1∑NZk∣N))
推荐上面的写法
E ( E ( ∑ k = 1 N Z k ∣ N ) ) = E ( N ∗ E ( Z 1 ) ) = E ( N ) ∗ E ( Z 1 ) E(E(\sum_{k=1}^{N}Z_k|N))= E(N*E(Z_1)) = E(N)*E(Z_1) E(E(k=1∑NZk∣N))=E(N∗E(Z1))=E(N)∗E(Z1)
重申一下,条件期望的原因就是各个击破。
(4) 条件期望与最小均方估计
条件期望与最小均方估计有非常密切的联系
比如我们有两个随机变量Y,Z,我们希望能用Z构成估计,让Z构成的估计尽可能的逼近Y,也就是我们想在均方意义下找最优估计
Y , Z → g ( Z ) Y, Z \rightarrow g(Z) Y,Z→g(Z)
m i n E [ ( Y − g ( Z ) ) 2 ] minE[(Y-g(Z))^2] minE[(Y−g(Z))2]
这个估计是有最优解的
g ( Z ) = E ( Y ∣ Z ) g(Z)= E(Y|Z) g(Z)=E(Y∣Z)
我们来验证这件事情
E
[
(
Y
−
g
(
Z
)
)
2
]
=
E
[
(
Y
−
E
(
Y
∣
Z
)
+
E
(
Y
∣
Z
)
−
g
(
Z
)
)
2
]
=
E
[
(
Y
−
E
(
Y
∣
Z
)
)
2
]
+
E
[
(
E
(
Y
∣
Z
)
−
g
(
Z
)
)
2
]
+
2
∗
E
[
(
Y
−
E
(
Y
∣
Z
)
)
∗
(
E
(
Y
∣
Z
)
−
g
(
Z
)
)
]
E[(Y-g(Z))^2] = E[(Y-E(Y|Z)+E(Y|Z)-g(Z))^2] \\ = E[(Y-E(Y|Z))^2] + E[(E(Y|Z)-g(Z))^2] +2*E[(Y-E(Y|Z))*(E(Y|Z)-g(Z))]
E[(Y−g(Z))2]=E[(Y−E(Y∣Z)+E(Y∣Z)−g(Z))2]=E[(Y−E(Y∣Z))2]+E[(E(Y∣Z)−g(Z))2]+2∗E[(Y−E(Y∣Z))∗(E(Y∣Z)−g(Z))]
我们把交叉项单独拿出来分析,因为我们希望他能够等于0
经过分析我们发现,这个期望里面有Z和Y两种随机性,我们发现有1个是Y引起的,3个是Z引起的,所以我们利用条件期望的手段,先条件住Z求Y,然后再回来处理Z
把后面部分取出来,根据期望的线性性质进行拆解
E [ ( Y − E ( Y ∣ Z ) ) ∗ ( E ( Y ∣ Z ) − g ( Z ) ) ] = E ( E Y ( ( Y − E ( Y ∣ Z ) ) ∗ ( E ( Y ∣ Z ) − g ( Z ) ) ∣ Z ) ) = E [ ( E ( Y ∣ Z ) − g ( Z ) ) ∗ E Y ( ( Y − E ( Y ∣ Z ) ) ∣ Z ) ] E[(Y-E(Y|Z))*(E(Y|Z)-g(Z))] = E(E_Y((Y-E(Y|Z))*(E(Y|Z)-g(Z))|Z)) \\ = E[(E(Y|Z)-g(Z))*E_Y((Y-E(Y|Z))|Z)] E[(Y−E(Y∣Z))∗(E(Y∣Z)−g(Z))]=E(EY((Y−E(Y∣Z))∗(E(Y∣Z)−g(Z))∣Z))=E[(E(Y∣Z)−g(Z))∗EY((Y−E(Y∣Z))∣Z)]
里面用到了条件期望的性质2,E(Y|Z)的随机变量是Z,因此对Y的条件期望中,该项可以看做是常数项,因此可以提出来。同理交叉项的后一部分也可以拆解
E ( ( Y − E ( Y ∣ Z ) ) ∣ Z ) = E ( Y ∣ Z ) − E ( E ( Y ∣ Z ) ) ∣ Z ) = E ( Y ∣ Z ) − E ( Y ∣ Z ) ∗ E ( 1 ∣ Z ) = E ( Y ∣ Z ) − E ( Y ∣ Z ) ∗ 1 = 0 E((Y-E(Y|Z))|Z) \\ = E(Y|Z)-E(E(Y|Z))|Z) \\ = E(Y|Z)-E(Y|Z)*E(1|Z) \\ = E(Y|Z)-E(Y|Z)*1 = 0 E((Y−E(Y∣Z))∣Z)=E(Y∣Z)−E(E(Y∣Z))∣Z)=E(Y∣Z)−E(Y∣Z)∗E(1∣Z)=E(Y∣Z)−E(Y∣Z)∗1=0
因此后面第三部分的交叉项确实为0
因此
E [ ( Y − g ( Z ) ) 2 ] = E [ ( Y − E ( Y ∣ Z ) ) 2 ] + E [ ( E ( Y ∣ Z ) − g ( Z ) ) 2 ] E[(Y-g(Z))^2] = E[(Y-E(Y|Z))^2] + E[(E(Y|Z)-g(Z))^2] E[(Y−g(Z))2]=E[(Y−E(Y∣Z))2]+E[(E(Y∣Z)−g(Z))2]
这是个平方和,当下式满足时,均方距离最短
g ( Z ) = E ( Y ∣ Z ) g(Z) = E(Y|Z) g(Z)=E(Y∣Z)
3.3.1.2 条件方差
(1) 条件方差的概念
除了条件期望,我们还要引入一个条件方差
什么是条件方差?
V a r ( Y ) = E [ ( Y − E ( Y ) ) 2 ] V a r ( Y ∣ Z ) = E [ ( Y − E ( Y ∣ Z ) ) 2 ∣ Z ] Var(Y) = E[(Y-E(Y))^2] \\ Var(Y|Z) = E[(Y-E(Y|Z))^2|Z] Var(Y)=E[(Y−E(Y))2]Var(Y∣Z)=E[(Y−E(Y∣Z))2∣Z]
条件方差就是在方差的定义上,把所有期望变成条件期望。
条件方差也是个随机变量
(2) 条件方差的性质
条件期望再期望等于没有条件的期望
E
(
E
(
Y
∣
Z
)
)
=
E
(
Y
)
E(E(Y|Z)) = E(Y)
E(E(Y∣Z))=E(Y)
那条件方差满足什么等式呢?
方差就是条件方差的期望加条件期望的方差
V
a
r
(
Y
)
=
E
(
V
a
r
(
Y
∣
Z
)
)
+
V
a
r
(
E
(
Y
∣
Z
)
)
Var(Y) = E(Var(Y|Z))+Var(E(Y|Z))
Var(Y)=E(Var(Y∣Z))+Var(E(Y∣Z))
证明
V a r ( Y ) = E [ ( Y − E ( Y ) ) 2 ] = E [ ( Y − E ( Y ∣ Z ) + E ( Y ∣ Z ) − E ( Y ) ) 2 ] = E [ ( Y − E ( Y ∣ Z ) ) 2 ] + E [ ( E ( Y ∣ Z ) − E ( Y ) ) 2 ] + 2 ∗ E [ ( Y − E ( Y ∣ Z ) ) ∗ ( E ( Y ∣ Z ) − E ( Y ) ) ] Var(Y) = E[(Y-E(Y))^2] \\ = E[(Y-E(Y|Z)+E(Y|Z)-E(Y))^2] \\ = E[(Y-E(Y|Z))^2]+E[(E(Y|Z)-E(Y))^2]+ 2*E[(Y-E(Y|Z))*(E(Y|Z)-E(Y))] Var(Y)=E[(Y−E(Y))2]=E[(Y−E(Y∣Z)+E(Y∣Z)−E(Y))2]=E[(Y−E(Y∣Z))2]+E[(E(Y∣Z)−E(Y))2]+2∗E[(Y−E(Y∣Z))∗(E(Y∣Z)−E(Y))]
经典环节,证明交叉项是0
E [ ( Y − E ( Y ∣ Z ) ) ∗ ( E ( Y ∣ Z ) − E ( Y ) ) ] = E [ E Y ( ( Y − E ( Y ∣ Z ) ) ∗ ( E ( Y ∣ Z ) − E ( Y ) ) ∣ Z ) ] = E [ ( E ( Y ∣ Z ) − E ( Y ) ) ∗ E Y ( ( Y − E ( Y ∣ Z ) ) ∣ Z ) ] E[(Y-E(Y|Z))*(E(Y|Z)-E(Y))] \\ = E[E_Y((Y-E(Y|Z))*(E(Y|Z)-E(Y))|Z)] \\ = E[(E(Y|Z)-E(Y))*E_Y((Y-E(Y|Z))|Z)] E[(Y−E(Y∣Z))∗(E(Y∣Z)−E(Y))]=E[EY((Y−E(Y∣Z))∗(E(Y∣Z)−E(Y))∣Z)]=E[(E(Y∣Z)−E(Y))∗EY((Y−E(Y∣Z))∣Z)]
对后一部分单独分析
E Y ( ( Y − E ( Y ∣ Z ) ) ∣ Z ) = E Y ( Y ∣ Z ) − E Y [ E ( Y ∣ Z ) ∣ Z ] = E Y ( Y ∣ Z ) − E ( Y ∣ Z ) ∗ E Y [ 1 ∣ Z ] = E Y ( Y ∣ Z ) − E ( Y ∣ Z ) ∗ 1 = 0 E_Y((Y-E(Y|Z))|Z) \\ = E_Y(Y|Z)- E_Y[E(Y|Z)|Z] \\ = E_Y(Y|Z) - E(Y|Z)* E_Y[1|Z] \\ = E_Y(Y|Z) - E(Y|Z)*1 \\ = 0 EY((Y−E(Y∣Z))∣Z)=EY(Y∣Z)−EY[E(Y∣Z)∣Z]=EY(Y∣Z)−E(Y∣Z)∗EY[1∣Z]=EY(Y∣Z)−E(Y∣Z)∗1=0
可以证明交叉项为0
V
a
r
(
Y
)
=
E
[
(
Y
−
E
(
Y
∣
Z
)
)
2
]
+
E
[
(
E
(
Y
∣
Z
)
−
E
(
Y
)
)
2
]
Var(Y) =E[(Y-E(Y|Z))^2]+E[(E(Y|Z)-E(Y))^2]
Var(Y)=E[(Y−E(Y∣Z))2]+E[(E(Y∣Z)−E(Y))2]
可以看出来后一项是条件期望的方差
V a r ( Y ) = E [ ( Y − E ( Y ∣ Z ) ) 2 ] + E [ ( E ( Y ∣ Z ) − E ( Y ) ) 2 ] = E [ ( Y − E ( Y ∣ Z ) ) 2 ] + V a r [ E ( Y ∣ Z ) ] Var(Y) = E[(Y-E(Y|Z))^2]+E[(E(Y|Z)-E(Y))^2] \\ = E[(Y-E(Y|Z))^2] + Var[E(Y|Z)] Var(Y)=E[(Y−E(Y∣Z))2]+E[(E(Y∣Z)−E(Y))2]=E[(Y−E(Y∣Z))2]+Var[E(Y∣Z)]
我们来看前一项,先找找条件方差的定义
V a r ( Y ∣ Z ) = E [ ( Y − E ( Y ∣ Z ) ) 2 ∣ Z ] Var(Y|Z) = E[(Y-E(Y|Z))^2|Z] Var(Y∣Z)=E[(Y−E(Y∣Z))2∣Z]
我们发现
E [ V a r ( Y ∣ Z ) ] = E ( E Y ( ( Y − E ( Y ∣ Z ) ) 2 ∣ Z ) ) = E [ ( Y − E ( Y ∣ Z ) ) 2 ] E[Var(Y|Z)] = E(E_Y((Y-E(Y|Z))^2|Z) ) = E[(Y-E(Y|Z))^2] E[Var(Y∣Z)]=E(EY((Y−E(Y∣Z))2∣Z))=E[(Y−E(Y∣Z))2]
所以我们就得到了
V a r ( Y ) = E [ ( Y − E ( Y ∣ Z ) ) 2 ] + V a r [ E ( Y ∣ Z ) ] = E [ V a r ( Y ∣ Z ) ] + V a r [ E ( Y ∣ Z ) ] Var(Y) = E[(Y-E(Y|Z))^2] + Var[E(Y|Z)] = E[Var(Y|Z)] + Var[E(Y|Z)] Var(Y)=E[(Y−E(Y∣Z))2]+Var[E(Y∣Z)]=E[Var(Y∣Z)]+Var[E(Y∣Z)]
3.3.1.3 充分统计量
下面我们要引入一个概念,充分统计量 Sufficient Statistic
什么是充分统计量呢? 我们先举个例子,说明一下什么样的处理叫做尽可能保留参数的信息
(1)尽可能保留参数的信息
( Z 1 , . . . , Z n ) = Z ∼ f ( Z , θ ) (Z_1,...,Z_n) = Z \sim f(Z, \theta) (Z1,...,Zn)=Z∼f(Z,θ)
假设我们有一组参数Z,并且符合一定的参数化模型
我们通过对Z进行处理,得到对θ的估计
θ ^ ( Z ) \hat \theta(Z) θ^(Z)
希望这个处理尽可能包含所有关于θ的信息,下面举例说明一下
- 信息全部丢失的例子
把这个参数化模型进行细化,假设Z服从正态分布,这里需要估计的参数是均值
Z ∼ f ( Z , θ ) = N ( θ , 1 ) Z \sim f(Z, \theta) = N(θ,1) Z∼f(Z,θ)=N(θ,1)
我们随便定义一种处理方法
θ ^ ( Z ) = Z 1 − Z 2 \hat \theta(Z) = Z_1 - Z_2 θ^(Z)=Z1−Z2
这种处理方法可以得到一个新的分布
θ ^ ( Z ) = Z 1 − Z 2 ∼ N ( 0 , 2 ) \hat \theta(Z) = Z_1 - Z_2 \sim N(0,2) θ^(Z)=Z1−Z2∼N(0,2)
可以看到,这种处理方法就把θ抹掉了,对θ的估计毫无帮助。因此这种统计方法是多余的
- 信息尽可能保留的例子
有的统计方法可能就很好的捕获到了与θ的信息
这里我们把Z的分布改为均匀分布,需要估计的是均匀分布的范围
Z ∼ f ( Z , θ ) = U ( 0 , θ ) Z \sim f(Z, \theta) = U(0,\theta) Z∼f(Z,θ)=U(0,θ)
基于这些数据我们构造了两种处理方法,哪种处理方法能够保留θ的更多信息呢
θ ^ 1 ( Z ) = m i n ( Z 1 , . . . , Z n ) \hat \theta_1(Z) = min(Z_1,...,Z_n) θ^1(Z)=min(Z1,...,Zn)
θ ^ 2 ( Z ) = m a x ( Z 1 , . . . , Z n ) \hat \theta_2(Z) = max(Z_1,...,Z_n) θ^2(Z)=max(Z1,...,Zn)
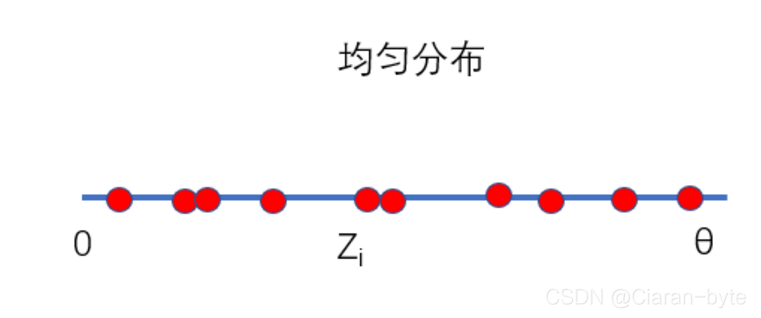
显然肯定是取最大值,因为θ是最大的边界点,肯定不小于采样值中的最大值。因此处理方法2尽可能的保留了估计参数的信息
(2)引入充分统计量
有没有这样的统计,能够把θ的相关信息捕获干净,浓缩采样信息中所有关系θ的信息,并且不会丢失掉有关θ的全部信息?
其实是有的,而且这种统计就叫做充分统计,这个概念来源于Fisher 1920年
采样数据原本是依赖于θ的,如果让某一个统计,把θ给条件住,然后计算Z的概率分布,就和θ无关了。这样的统计就叫做充分统计,所有的θ的信息都在这个条件分布里面了
f
(
Z
∣
θ
^
(
Z
)
=
t
)
i
n
d
e
p
e
n
d
e
n
t
o
f
θ
f(Z|\hat \theta(Z) = t) \quad\quad independent \quad of \quad θ
f(Z∣θ^(Z)=t)independentofθ
因此如果我们要做uniform的事情,就必须要基于这个充分统计量了
(3)举例
Z 1 . . . . , Z n ∼ B ( m , θ ) Z_1....,Z_n \sim B(m,θ) Z1....,Zn∼B(m,θ)
假设Z符合二项分布,m是打枪,θ是命中率,m是已知的,θ是未知的,Z是命中枪数
求一下Z的联合分布函数(就是所有Z成立的概率乘积)
f
(
Z
1
,
.
.
.
.
,
Z
n
)
=
∏
k
=
1
n
(
m
Z
k
)
θ
Z
k
(
1
−
θ
)
m
−
Z
k
f(Z_1,....,Z_n) = \prod_{k=1}^{n} \begin{pmatrix} m \\ Z_k \end{pmatrix}\theta ^{Z_k}(1- \theta)^{m-Z_k}
f(Z1,....,Zn)=k=1∏n(mZk)θZk(1−θ)m−Zk
证明他的充分就是下面这个
θ
^
(
Z
)
=
Z
1
+
.
.
.
+
Z
n
\hat \theta(Z) = Z_1 +...+Z_n
θ^(Z)=Z1+...+Zn
也就是所有命中枪数的和能够保留所有的参数估计信息
证明
f
(
Z
1
,
.
.
.
,
Z
n
∣
θ
(
Z
)
=
N
)
=
P
(
Z
1
,
.
.
.
,
Z
n
,
θ
(
Z
)
=
N
)
P
(
θ
(
Z
)
=
N
)
=
(
∏
k
=
1
n
(
m
Z
k
)
)
θ
N
(
1
−
θ
)
m
n
−
N
(
n
m
N
)
θ
N
(
1
−
θ
)
m
n
−
N
=
∏
k
=
1
n
(
m
Z
k
)
(
n
m
N
)
f(Z_1,...,Z_n | θ(Z)=N) \\ = \frac{P(Z_1,...,Z_n , θ(Z)=N) }{P(θ(Z)=N)} \\ = \frac{(\prod_{k=1}^{n} \begin{pmatrix} m \\ Z_k \end{pmatrix})\theta^N(1-\theta)^{mn-N}}{\begin{pmatrix} nm \\ N \end{pmatrix}\theta^N(1-\theta)^{mn-N}} \\ =\frac{\prod_{k=1}^{n} \begin{pmatrix} m \\ Z_k \end{pmatrix}}{\begin{pmatrix} nm \\ N \end{pmatrix}}
f(Z1,...,Zn∣θ(Z)=N)=P(θ(Z)=N)P(Z1,...,Zn,θ(Z)=N)=(nmN)θN(1−θ)mn−N(∏k=1n(mZk))θN(1−θ)mn−N=(nmN)∏k=1n(mZk)
我们得到一个与θ无关的东西,说明是完全统计函数,确实就是我们猜想的那个。因为这个统计方法,捕捉到了所有与命中率有关的信息。
不过,完全统计量是非常不好找的。
3.3.2 Rao-Blackwell定理
继续来研究最优问题,在这里,我们要给出一个基于MVUE标准的求最优的过程
3.3.2.1 条件
我们通过处理我们的采样数据,已经得到了一个θ1,虽然不是最优的。但是是无偏的。
找到一个θ2,不要求其无偏,但是要求他是充分统计量
θ ^ 1 ( Z ) E ( θ ^ 1 ) = θ θ ^ 2 ( Z ) 充 分 统 计 量 \hat \theta_1(Z) \\ E(\hat \theta_1) = \theta \\ \hat \theta_2(Z) 充分统计量 θ^1(Z)E(θ^1)=θθ^2(Z)充分统计量
3.3.2.2 方法
我们通过θ2不断的对θ1进行优化,从而得到更好的估计方法,这个方法可以反复用下去
θ ^ 3 = E ( θ ^ 1 ∣ θ ^ 2 ) \hat \theta _3 = E(\hat \theta _1 | \hat \theta_2) θ^3=E(θ^1∣θ^2)
3.3.2.3 断言
我们可以断言两点
E ( θ ^ 3 ) = θ v a r ( θ ^ 3 ) ≤ E ( θ ^ 1 ) E(\hat \theta_3) = \theta \\ var(\hat \theta_3) \leq E(\hat \theta_1) E(θ^3)=θvar(θ^3)≤E(θ^1)
- 【1】θ3 一定是无偏的
E ( θ ^ 3 ) = E ( θ ^ 1 ∣ θ ^ 2 ) = E ( θ ^ 1 ) = θ E(\hat \theta_3) = E(\hat \theta _1 | \hat \theta_2) = E(\hat \theta _1) = \theta E(θ^3)=E(θ^1∣θ^2)=E(θ^1)=θ
- 【2】Var(θ3)一定小于Var(θ1)
V a r ( θ 1 ) = E [ V a r ( θ 1 ∣ θ 2 ) ] + V a r [ E ( θ 1 ∣ θ 2 ) ] = u ( > 0 ) + V a r ( θ 3 ) Var(\theta_1)=E[Var(\theta_1|\theta_2)] + Var[E(\theta_1|\theta_2)] = u(>0) + Var(\theta_3) Var(θ1)=E[Var(θ1∣θ2)]+Var[E(θ1∣θ2)]=u(>0)+Var(θ3)
所以一定Var(θ_3)小
3.3.2.4 关于θ2必须是充分统计量的解释
看起了上面的断言没有用到θ2充分统计量的条件,实际上用到了。
因为只有用充分统计量,他得到的θ3才是独立于θ的,我们构筑的统计方法,必须是只能依赖于采样数据,而不依赖于未知量,得到的θ3才是合乎规定的
这种方法叫做 Rao-Blackwell,以一个任意的原始估计为起点,寻找最小方差无偏估计量(MVUE)
以上是对一种估计方法的优化方案。如果觉得不够,可以反复的使用。但是不能保证每一次都是真正下降,因为它是小于等于。因此,我们需要知道这个估计有没有下界。这是下面要讨论的问题
3.4 信号处理方法优化的下限
3.4.1 概述
通过rao-blackwell优化,我们可以基于已经知道的一种估计方法,继续改进然后寻找更好的估计。但是,我们想知道,这样的改进是否是有尽头的,以及有没有收敛的趋势。如果收敛的话,是什么样的。
3.4.3 Lehmann-Scheffe theorem
3.4.3.1 完备统计量
这个时候我们需要引入新概念:complete statistics 完备统计
假设统计T是完备的,T是依赖于样本的一个函数,有
T
(
Z
1
,
Z
2
,
.
.
.
,
Z
n
)
=
T
T(Z_1,Z_2,...,Z_n) = T
T(Z1,Z2,...,Zn)=T
完备是指,统计里已经不包含任何与\hat θ无关的信息了。
完备统计通常只存在与纸面上,我们几乎不可能找到一个这样的统计。
完备统计具有这样的性质
有任意的函数g,g能作用在完备统计量T上,也就是g(T),如果E(g(T))=0,那么g(T)恒为0
∀ g , 有 g ( T ) E ( g ( T ) ) = 0 = > P ( g ( T ) = 0 ) = 1 \forall g,有g(T) \\ E(g(T)) =0 => P(g(T)=0)=1 ∀g,有g(T)E(g(T))=0=>P(g(T)=0)=1
3.4.3.2 优化极限的确定
能够确定最小方差无偏估计的最小方差的定量叫做***Lehmann-Scheffe theorem***
假定S是一个统计,S是无偏的,构造一个新的统计,这个新统计依赖T,这个T是充分且完备的统计,则S* = E(S|T)就是MVUE
S
,
E
(
S
)
=
0
T
:
s
u
f
f
i
c
i
e
n
t
a
n
d
c
o
m
p
l
e
t
e
M
V
U
E
=
>
S
∗
=
E
(
S
∣
T
)
S, E(S) = 0\\ T: sufficient \quad and \quad complete \\ MVUE=> S* = E(S|T)
S,E(S)=0T:sufficientandcompleteMVUE=>S∗=E(S∣T)
3.4.3.3 定理证明
假定任意统计量θ都是无偏的
∀ θ ^ , E ( θ ^ ) = θ \forall \hat \theta,E(\hat \theta)= \theta ∀θ^,E(θ^)=θ
我们只需要证明S*的方差比任意统计都小即可,即下式成立
V
a
r
(
θ
^
)
>
=
V
a
r
(
S
∗
)
Var(\hat \theta) >= Var(S^*)
Var(θ^)>=Var(S∗)
我们定义统计量θ*
θ ^ ∗ = E ( θ ^ ∣ T ) \hat \theta^*= E(\hat \theta |T) θ^∗=E(θ^∣T)
这个统计量也是无偏的,因为条件均值的均值等于均值
E
(
θ
^
∗
)
=
E
(
E
(
θ
^
∣
T
)
)
=
θ
E(\hat \theta^ *)= E(E(\hat \theta |T)) = \theta
E(θ^∗)=E(E(θ^∣T))=θ
因为T是充分统计量,因此与 \hat θ无关,所以由rao-blackwell
V a r ( θ ^ ∗ ) < = V a r ( θ ^ ) Var(\hat \theta^ *) <= Var(\hat \theta) Var(θ^∗)<=Var(θ^)
因为\hat θ 代表任意统计量,而 \hat θ *小于任意统计量的方差,所以 \hat θ *就是最小方差无偏估计
因为二者都是无偏估计,所以
E
(
θ
^
∗
−
S
∗
)
=
0
E(\hat \theta ^* - S^*) = 0
E(θ^∗−S∗)=0
因为S*和θ*都是T的函数,所以二者相减也是T的函数
E ( θ ^ ∗ − S ∗ ) = E ( g ( T ) ) = 0 E(\hat \theta ^* - S^*) = E(g(T)) = 0 E(θ^∗−S∗)=E(g(T))=0
所以,根据完备统计量的性质
g ( T ) = θ ^ ∗ − S ∗ = 0 g(T)= \hat \theta ^* - S^* = 0 g(T)=θ^∗−S∗=0
因此二者是一回事。所以S*就是MVUE,因为他比任意\hat θ都有更小的方差
3.4.3.4 注意
这种定理是没有办法解决实际问题的。因为实际中,我们没有办法找到完备统计量,这个方法只能随便看看,并不接地气。开始我们不懂MVUE是什么,然后我们引入完备统计量解释了MVUE,但是完备统计量是什么又没办法定义,就是用一个不知道解决了另外一个不知道,仅此而已。
3.4.4 误差估计下界 lower bound of estimation
3.4.4.1 概述
我们确实没有办法找到准确的MVUE,所以我们只能放宽要求,找到一个下界,最小方差肯定不大于这个下界。
给一个下界其实要比找到真正的MVUE更有价值。
通过给定下界,能够找到一部分的问题的最小方差无偏估计
3.4.4.2 影响下界选择的因素的猜测
现在给定一个模型,方便举例子。假设采样数据满足高斯分布,其中Z未知,σ是已知的
Z N ( θ , σ 2 ) Z ~N(\theta,\sigma ^2) Z N(θ,σ2)
f
(
x
,
θ
)
=
1
2
∗
π
σ
e
x
p
(
−
(
x
−
θ
)
2
2
σ
2
)
f(x,\theta) = \frac{1}{\sqrt{2*\pi}\sigma}exp(-\frac{(x-\theta)^2}{2\sigma^2})
f(x,θ)=2∗πσ1exp(−2σ2(x−θ)2)
我们来感受一下估计误差会被哪些因素所左右。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WWouH5OO-1629965077114)(1D2E1BC73EA64AC8A855C8781007E0F1)]](https://img-blog.csdnimg.cn/37cf3e8b7a0846038ee082e192fb868a.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_Q1NETiBAQ2lhcmFuLWJ5dGU=,size_22,color_FFFFFF,t_70,g_se,x_16)
我们可以假设每个x是均值,θ是未知量
- 方差
如果图像可能是这两条,哪一条用来估计θ更加准确呢,答案是红色的那条,因为方差小
因此,我们猜测,不同模型有不同的估计下界,方差小的估计下界会更低一点。
- 曲率
从另外一个角度考虑。
我们如何描述红色和蓝色曲线的差异呢?
曲率。曲率代表曲线的弯曲程度,弯曲程度越大,曲率越大。直线的曲率是0。在曲线上某点的曲率,就是其内接圆的半径的倒数,这是曲率的定义
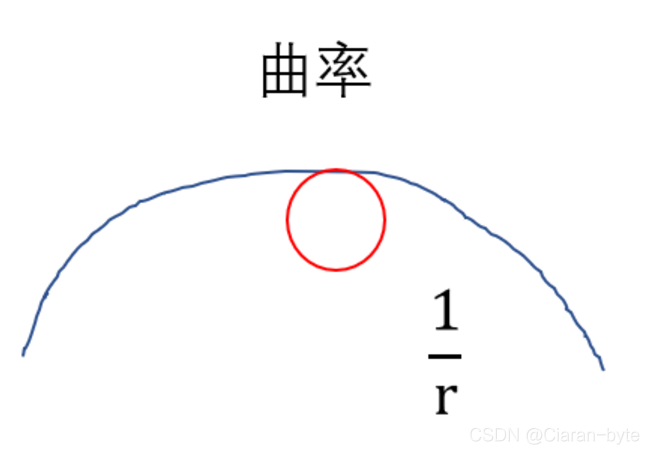
如果要估计的准,就是要在顶点位置弯曲要大,也就是曲率要大。曲率可能是估计下限能达到多少的一种度量
曲率与二阶导数有关系
∂ 2 ∂ θ 2 f ( Z , θ ) \frac{\partial^2}{\partial \theta^2} f(Z,\theta) ∂θ2∂2f(Z,θ)
但是Z是个随机变量,因此我们要对他求一下期望,去掉随机性
∂ 2 ∂ θ 2 f ( Z , θ ) = > E ( ∂ 2 ∂ θ 2 f ( Z , θ ) ) \frac{\partial^2}{\partial \theta^2} f(Z,\theta) => E(\frac{\partial^2}{\partial \theta^2} f(Z,\theta)) ∂θ2∂2f(Z,θ)=>E(∂θ2∂2f(Z,θ))
- 变化率
我们还有一个感觉,我们来看看一阶导数。
一阶导数代表变化率,随着θ变化,一阶导数会有什么变化。变化率大意味着,θ稍微一变,模型具有巨大变化,采样数据就有巨大变化,对θ是非常敏感的。说明数据就包含θ的更多信息。因此变化率越大越好。
我们通常求他绝对值的平方
∣ ∂ ∂ θ f ( Z , θ ) ∣ 2 | \frac{\partial}{\partial \theta}f(Z,\theta)|^2 ∣∂θ∂f(Z,θ)∣2
同样Z是个随机变量,因此我们要对他求一下期望,去掉随机性
∣ ∂ ∂ θ f ( Z , θ ) ∣ 2 = > E ( ∣ ∂ ∂ θ f ( Z , θ ) ∣ 2 ) | \frac{\partial}{\partial \theta}f(Z,\theta)|^2 => E(| \frac{\partial}{\partial \theta}f(Z,\theta)|^2) ∣∂θ∂f(Z,θ)∣2=>E(∣∂θ∂f(Z,θ)∣2)
3.4.4.2 柯西施瓦茨不等式
我们接下来需要回顾一下柯西不等式的概念,后面要用。
(1) 内积
柯西不等式实质是线性代数中内积的性质,我们先来看一下内积
内积的符号
H
x
H
=
R
HxH = R
HxH=R
内积的性质
- 对称性
< x , y > = < y , x > <x,y> = <y,x> <x,y>=<y,x>
- 非负性
< x , x > ≥ 0 < x , x > = 0 ⟺ x = 0 <x,x> \quad \geq 0 \\ <x,x> \quad =0 \iff x=0 <x,x>≥0<x,x>=0⟺x=0
- 双线性性质
固定住内积的其中一个,对另外一个进行线性操作,得到的结果也是线性的变换
<
α
x
+
β
y
,
z
>
=
α
<
x
,
z
>
+
β
<
y
,
z
>
<
x
,
α
y
+
β
z
>
=
α
<
x
,
y
>
+
β
<
x
,
z
>
<αx+βy,z> = α<x,z> + β<y,z> <x,αy+βz> = α<x,y> + β<x,z>
<αx+βy,z>=α<x,z>+β<y,z><x,αy+βz>=α<x,y>+β<x,z>
双线性性质在不同空间表现如下:
如果线性空间是欧式空间,则内积
H
=
R
n
{
x
=
(
X
1
,
.
.
.
,
X
n
)
y
=
(
Y
1
,
.
.
.
,
Y
n
)
=
>
<
x
,
y
>
=
∑
k
=
1
n
X
k
Y
k
H = R^n \\ \begin{cases} x = (X_1,...,X_n) \\ y = (Y_1,...,Y_n) \end{cases} => \quad <x,y> = \sum^n_{k=1}X_kY_k
H=Rn{x=(X1,...,Xn)y=(Y1,...,Yn)=><x,y>=k=1∑nXkYk
如果线性空间的平方可积的函数,内积就是两个函数乘在一起的积分
H = L 2 ( R ) { x = f ( t ) y = g ( t ) = > < x , y > = ∫ − ∞ + ∞ f ( t ) g ( t ) d t H = L^2(R) \\ \begin{cases} x = f(t) \\ y = g(t) \end{cases} => \quad <x,y> = \int_{-\infty}^{+\infty}f(t)g(t)dt H=L2(R){x=f(t)y=g(t)=><x,y>=∫−∞+∞f(t)g(t)dt
(2) cauaky-schwarz
cauaky-schwarz不等式本质上是内积的性质
∣ < x , y > ∣ 2 ≤ < x , x > < y , y > |<x,y>|^2 \leq \quad <x,x><y,y> ∣<x,y>∣2≤<x,x><y,y>
欧式空间
( ∑ k = 1 n X k Y k ) 2 ≤ ( ∑ k = 1 n X k 2 ) ( ∑ k = 1 n Y k 2 ) (\sum^n_{k=1}X_kY_k)^2 \leq(\sum^n_{k=1}X_k^2)(\sum^n_{k=1}Y_k^2) (k=1∑nXkYk)2≤(k=1∑nXk2)(k=1∑nYk2)
平方可积的函数空间
∣ ∫ − ∞ + ∞ f ( t ) g ( t ) d t ∣ 2 ≤ ∫ − ∞ + ∞ f 2 ( t ) d t ∫ − ∞ + ∞ g 2 ( t ) d t |\int_{-\infty}^{+\infty}f(t)g(t)dt|^2 \leq\int_{-\infty}^{+\infty}f^2(t)dt\int_{-\infty}^{+\infty}g^2(t)dt ∣∫−∞+∞f(t)g(t)dt∣2≤∫−∞+∞f2(t)dt∫−∞+∞g2(t)dt
(2) cauaky-schwarz 证明
0 ≤ g ( α ) = < α x + y , α x + y > 0 \leq g(\alpha) = <\alpha x+y,\alpha x+y> 0≤g(α)=<αx+y,αx+y>
用内积双线性性质和对称性质展开
0 ≤ g ( α ) = < x , x > α 2 + 2 α < x , y > + < y , y > 0 \leq g(\alpha) = <x,x> \alpha^2 +2\alpha <x,y>+<y,y> 0≤g(α)=<x,x>α2+2α<x,y>+<y,y>
这是个开口向上的抛物线,一定有0或2个根,故
Δ = b 2 − 4 a c = 4 < x , y > 2 − 4 < x , x > < y , y > ≤ 0 = > < x , y > 2 ≤ < x , x > < y , y > \Delta = b^2-4ac =\quad 4<x,y>^2 - 4<x,x><y,y> \quad\leq 0 \\ => <x,y>^2 \quad \leq \quad <x,x><y,y> Δ=b2−4ac=4<x,y>2−4<x,x><y,y>≤0=><x,y>2≤<x,x><y,y>
3.4.4.3 克拉美罗下界 CRLB
(1) 与一阶函数有关的克拉美罗下界的表示
现在我们可以研究,估计的下界到底在哪里了。
我们有一些基本事实
∫ − ∞ + ∞ f ( x , θ ) d x = 1 ( 1 ) \int_{-\infty}^{+\infty} f(x,\theta)dx = 1 \quad\quad\quad\quad\quad\quad\quad\quad\quad(1) ∫−∞+∞f(x,θ)dx=1(1)
∫ − ∞ + ∞ θ ^ ( x ) f ( x , θ ) d x = E ( θ ^ ) = θ ( 2 ) \int_{-\infty}^{+\infty} \hat \theta(x)f(x,\theta)dx = E(\hat \theta) = \theta \quad\quad\quad\quad(2) ∫−∞+∞θ^(x)f(x,θ)dx=E(θ^)=θ(2)
由第一个式子推出
∂ ∂ θ ∫ − ∞ + ∞ f ( x , θ ) d x = ∫ − ∞ + ∞ ∂ ∂ θ f ( x , θ ) d x = ∂ ∂ θ ( 1 ) = 0 = > ∫ − ∞ + ∞ θ ∂ ∂ θ f ( x , θ ) d x = 0 ( 3 ) \frac{\partial}{\partial \theta}\int_{-\infty}^{+\infty} f(x,\theta)dx = \int_{-\infty}^{+\infty} \frac{\partial}{\partial \theta}f(x,\theta)dx = \frac{\partial}{\partial \theta}(1) = 0 \\ => \int_{-\infty}^{+\infty} \theta\frac{\partial}{\partial \theta}f(x,\theta)dx=0 \quad\quad(3) ∂θ∂∫−∞+∞f(x,θ)dx=∫−∞+∞∂θ∂f(x,θ)dx=∂θ∂(1)=0=>∫−∞+∞θ∂θ∂f(x,θ)dx=0(3)
由第二个式子
∂ ∂ θ ∫ − ∞ + ∞ θ ^ ( x ) f ( x , θ ) d x = ∫ − ∞ + ∞ θ ^ ( x ) ∂ ∂ θ f ( x , θ ) d x = ∂ ∂ θ ( θ ) = 1 ( 4 ) \frac{\partial}{\partial \theta}\int_{-\infty}^{+\infty} \hat \theta(x)f(x,\theta)dx =\int_{-\infty}^{+\infty} \hat \theta(x)\frac{\partial}{\partial \theta}f(x,\theta)dx = \frac{\partial}{\partial \theta}(\theta) =1\quad\quad(4) ∂θ∂∫−∞+∞θ^(x)f(x,θ)dx=∫−∞+∞θ^(x)∂θ∂f(x,θ)dx=∂θ∂(θ)=1(4)
(4)-(3)
∫ − ∞ + ∞ ( θ ^ − θ ) [ ∂ ∂ θ f ( x , θ ) ] d x = 1 \int_{-\infty}^{+\infty} (\hat \theta- \theta) [\frac{\partial}{\partial \theta}f(x,\theta)]dx = 1 ∫−∞+∞(θ^−θ)[∂θ∂f(x,θ)]dx=1
变一下形
= > ∫ − ∞ + ∞ ( θ ^ − θ ) [ ∂ ∂ θ ( l n f ( x , θ ) ) ] f ( x , θ ) d x = 1 =>\int_{-\infty}^{+\infty} (\hat \theta- \theta)[\frac{\partial}{\partial \theta}(lnf(x,\theta))]f(x,\theta)dx = 1 =>∫−∞+∞(θ^−θ)[∂θ∂(lnf(x,θ))]f(x,θ)dx=1
把f(x,θ)拆解,便于使用柯西不等式
= > ∫ − ∞ + ∞ ( θ ^ − θ ) f ( x , θ ) [ ∂ ∂ θ ( l n f ( x , θ ) ) ] f ( x , θ ) d x = 1 =>\int_{-\infty}^{+\infty} (\hat \theta- \theta)\sqrt{f(x,\theta)}[\frac{\partial}{\partial \theta}(lnf(x,\theta))]\sqrt{f(x,\theta)}dx = 1 =>∫−∞+∞(θ^−θ)f(x,θ)[∂θ∂(lnf(x,θ))]f(x,θ)dx=1
使用柯西不等式可得
∫ − ∞ + ∞ ( θ ^ − θ ) 2 f ( x , θ ) d x ∫ − ∞ + ∞ [ ∂ ∂ θ ( l n f ( x , θ ) ) ] 2 f ( x , θ ) d x ≥ 1 \int_{-\infty}^{+\infty} (\hat \theta- \theta)^2f(x,\theta)dx\int_{-\infty}^{+\infty}[\frac{\partial}{\partial \theta}(lnf(x,\theta))]^2f(x,\theta)dx \geq1 ∫−∞+∞(θ^−θ)2f(x,θ)dx∫−∞+∞[∂θ∂(lnf(x,θ))]2f(x,θ)dx≥1`
V a r ( θ ^ ) ∗ E [ ( ∂ ∂ θ ( l n f ( x , θ ) ) ) 2 ] ≥ 1 Var(\hat \theta)*E[(\frac{\partial}{\partial \theta}(lnf(x,\theta)))^2] \geq1 Var(θ^)∗E[(∂θ∂(lnf(x,θ)))2]≥1
可得下界
V a r ( θ ^ ) ≥ I − 1 ( Q ) Var(\hat \theta) \geq I^{-1}(Q) Var(θ^)≥I−1(Q)
I ( Q ) = E [ ( ∂ ∂ θ ( l n f ( x , θ ) ) ) 2 ] I(Q) = E[(\frac{\partial}{\partial \theta}(lnf(x,\theta)))^2] I(Q)=E[(∂θ∂(lnf(x,θ)))2]
对于任意估计,这个下界都是有效的。这个下界仅仅依赖于统计模型,是universal的
这个下界与我们的一阶导数的感觉是差不多的
这个叫***克拉美罗下界***,cramer-rao lower bound,I(θ)叫做fisher information(fisher 信息量)
克拉美罗下界告诉我们,任何估计都是有下界的,这个下界只与统计模型有关,与估计方法没有关系,是对估计性能的总体的约束
(2) 与二阶函数有关的克拉美罗下界的表示
下面通过计算告诉大家,二阶导数的感觉也是对的
∫ − ∞ + ∞ f ( x , θ ) d x = 1 = > ∫ − ∞ + ∞ [ ∂ ∂ θ f ( x , θ ) ] d x = 0 \int_{-\infty}^{+\infty} f(x,\theta)dx = 1 \\ => \int_{-\infty}^{+\infty} [\frac{\partial}{\partial \theta}f(x,\theta)]dx=0 ∫−∞+∞f(x,θ)dx=1=>∫−∞+∞[∂θ∂f(x,θ)]dx=0
变形
∫ − ∞ + ∞ [ ∂ ∂ θ ( l n ( f ( x , θ ) ) ] f ( x , θ ) d x = 0 \int_{-\infty}^{+\infty} [\frac{\partial}{\partial \theta}(ln(f(x,\theta))]f(x,\theta)dx=0 ∫−∞+∞[∂θ∂(ln(f(x,θ))]f(x,θ)dx=0
再求偏导数还是0
∂
∂
θ
∫
−
∞
+
∞
[
∂
∂
θ
(
l
n
(
f
(
x
,
θ
)
)
]
f
(
x
,
θ
)
d
x
=
0
\frac{\partial}{\partial \theta}\int_{-\infty}^{+\infty} [\frac{\partial}{\partial \theta}(ln(f(x,\theta))]f(x,\theta)dx=0
∂θ∂∫−∞+∞[∂θ∂(ln(f(x,θ))]f(x,θ)dx=0
使用乘法的导数计算规则进行计算
∫ − ∞ + ∞ [ ∂ 2 ∂ θ 2 ( l n ( f ( x , θ ) ) ] f ( x , θ ) d x + ∫ − ∞ + ∞ [ ∂ ∂ θ ( l n ( f ( x , θ ) ) ] [ ∂ ∂ θ f ( x , θ ) ] d x = 0 \int_{-\infty}^{+\infty} [\frac{\partial^2}{\partial \theta^2}(ln(f(x,\theta))]f(x,\theta)dx+\int_{-\infty}^{+\infty} [\frac{\partial}{\partial \theta}(ln(f(x,\theta))][\frac{\partial}{\partial \theta}f(x,\theta)]dx=0 ∫−∞+∞[∂θ2∂2(ln(f(x,θ))]f(x,θ)dx+∫−∞+∞[∂θ∂(ln(f(x,θ))][∂θ∂f(x,θ)]dx=0
继续变形
E ( ∂ 2 ∂ θ 2 ( l n ( f ( x , θ ) ) ) + ∫ − ∞ + ∞ [ ∂ ∂ θ ( l n ( f ( x , θ ) ) ] 2 f ( x , θ ) d x E ( ∂ 2 ∂ θ 2 ( l n ( f ( x , θ ) ) ) + E [ ( ∂ ∂ θ ( l n ( f ( x , θ ) ) ) 2 ] = 0 E(\frac{\partial^2}{\partial \theta^2}(ln(f(x,\theta)))+ \int_{-\infty}^{+\infty} [\frac{\partial}{\partial \theta}(ln(f(x,\theta))]^2f(x,\theta)dx \\ E(\frac{\partial^2}{\partial \theta^2}(ln(f(x,\theta)))+E[(\frac{\partial}{\partial \theta}(ln(f(x,\theta)))^2] =0 E(∂θ2∂2(ln(f(x,θ)))+∫−∞+∞[∂θ∂(ln(f(x,θ))]2f(x,θ)dxE(∂θ2∂2(ln(f(x,θ)))+E[(∂θ∂(ln(f(x,θ)))2]=0
说明克拉美罗下界也可以用二阶导来表示
I ( θ ) = − E ( ∂ 2 ∂ θ 2 ( l n ( f ( x , θ ) ) ) I(\theta) = -E(\frac{\partial^2}{\partial \theta^2}(ln(f(x,\theta))) I(θ)=−E(∂θ2∂2(ln(f(x,θ)))
因此曲率的感觉也是对的
(3) 克拉美罗下界计算的例子
我们在3.4.4.2中举了一个估计正态分布参数的例子,我们用这个例子求一下克拉美罗下界,同事验证一下我们关于σ^2能影响克拉美罗下界的感觉。其中σ是已知量,我们算一下fisher 信息量
X 1 , . . . , X n ∼ N ( θ , σ 2 ) = > I ( θ ) X_1,...,X_n \sim N(\theta,\sigma ^2) => I(\theta) X1,...,Xn∼N(θ,σ2)=>I(θ)
计算克拉美罗下界四部曲
- 第一步:写出分布或者模型,要写出联合分布
这里的联合分布就是n个不同高斯的乘积,因为每个变量都是独立同分布
f ( X 1 , . . . X n ) = ∏ k = 1 n 1 2 ∗ π σ e x p ( − ( X k − θ ) 2 2 σ 2 ) = ( 1 2 ∗ π σ ) n e x p ( − 1 2 σ 2 ∑ k = 1 n ( X k − θ ) 2 ) f(X_1,...X_n) = \prod_{k=1}^{n} \frac{1}{\sqrt{2*\pi}\sigma}exp(-\frac{(X_k-\theta)^2}{2\sigma^2}) \\ = (\frac{1}{\sqrt{2*\pi}\sigma})^nexp(-\frac{1}{2\sigma^2}\sum_{k=1}^{n}(X_k-\theta)^2) f(X1,...Xn)=k=1∏n2∗πσ1exp(−2σ2(Xk−θ)2)=(2∗πσ1)nexp(−2σ21k=1∑n(Xk−θ)2)
- 第二步:对分布取ln
l n f ( X 1 , . . . X n ) = − n ∗ l n ( 2 ∗ π σ ) − 1 2 σ 2 ∑ k = 1 n ( X k − θ ) 2 lnf(X_1,...X_n) = -n*ln(\sqrt{2*\pi}\sigma)-\frac{1}{2\sigma^2}\sum_{k=1}^{n}(X_k-\theta)^2 lnf(X1,...Xn)=−n∗ln(2∗πσ)−2σ21k=1∑n(Xk−θ)2
- 第三步:求两次导数或求一次导数取平方也行
∂ ∂ θ l n f ( X 1 , . . . X n ) = ∑ k = 1 n ( X k − θ ) σ 2 \frac{\partial}{\partial \theta}lnf(X_1,...X_n) = \frac{\sum_{k=1}^{n}(X_k-\theta)}{\sigma^2} ∂θ∂lnf(X1,...Xn)=σ2∑k=1n(Xk−θ)
∂ 2 ∂ θ 2 l n f ( X 1 , . . . X n ) = − n σ 2 \frac{\partial^2}{\partial \theta^2}lnf(X_1,...X_n) = - \frac{n}{\sigma^2} ∂θ2∂2lnf(X1,...Xn)=−σ2n
- 第四步:计算fisher信息量
克拉美罗下界就求出来了
∀ θ ^ , E ( θ ^ ) = θ V a r ( θ ^ ) ≥ I − 1 ( Q ) = σ 2 n \forall \hat \theta,E(\hat \theta)= \theta \\ Var(\hat \theta) \geq I^{-1}(Q) = \frac{\sigma^2}{n} ∀θ^,E(θ^)=θVar(θ^)≥I−1(Q)=nσ2
这个数其实就是多次求和取平均的操作能够得到的方差
V a r ( θ ^ ) = E ( θ ^ − θ ) 2 = E ( 1 n ∑ k = 1 n X k − θ ) 2 = 1 n 2 E ( ∑ k = 1 n ( X k − θ ) ) 2 = σ 2 n Var(\hat \theta) = E(\hat \theta- \theta)^2 = E(\frac{1}{n}\sum_{k=1}^{n}X_k - \theta)^2 \\ = \frac{1}{n^2}E(\sum_{k=1}^{n}(X_k - \theta))^2 = \frac{\sigma^2}{n} Var(θ^)=E(θ^−θ)2=E(n1k=1∑nXk−θ)2=n21E(k=1∑n(Xk−θ))2=nσ2
如果估计的方差达到了克拉美罗下界,就称这个估计是有效的
克拉美罗下界的计算条件,就叫做正则化条件。但是这里可以忽略。因为克拉美罗下界的条件一般都遇不到。
(4) 克拉美罗下界另外一种证明方法
克拉美罗下界证明的精髓其实就是柯西不等式。
使用相关的方法也能进行证明
柯西不等式的相关形式
E
2
(
Z
,
Y
)
≤
E
(
Z
2
)
∗
E
(
Y
2
)
E^2(Z,Y) \leq E(Z^2)*E(Y^2)
E2(Z,Y)≤E(Z2)∗E(Y2)
相关也是一种内积,因为它满足对称性、非负性、双线性性质。
< Z , Y > = E ( Z , Y ) E ( Z 2 ) = 0 = > P ( Z = 0 ) = 1 <Z,Y> = E(Z,Y) \\ E(Z^2) =0 => P(Z=0) =1 <Z,Y>=E(Z,Y)E(Z2)=0=>P(Z=0)=1
我们引入一个任意函数φ,有如下内积
E ( θ ^ − θ ) 2 ∗ E ( ϕ ( Z ) − E ( ϕ ( Z ) ) 2 E(\hat \theta - \theta)^2 *E(\phi(Z) - E(\phi(Z))^2 E(θ^−θ)2∗E(ϕ(Z)−E(ϕ(Z))2
使用柯西不等式
E ( θ ^ − θ ) 2 ∗ E ( ϕ ( Z ) − E ( ϕ ( Z ) ) 2 ≥ E 2 [ ( θ ^ − θ ) ( ϕ ( Z ) − E ( ϕ ( Z ) ) ] E(\hat \theta - \theta)^2 *E(\phi(Z) - E(\phi(Z))^2 \geq E^2[(\hat \theta - \theta)(\phi(Z) - E(\phi(Z))] E(θ^−θ)2∗E(ϕ(Z)−E(ϕ(Z))2≥E2[(θ^−θ)(ϕ(Z)−E(ϕ(Z))]
移项可得
E ( θ ^ − θ ) 2 ≥ E 2 [ ( θ ^ − θ ) ( ϕ ( Z ) − E ( ϕ ( Z ) ) ] E ( ϕ ( Z ) − E ( ϕ ( Z ) ) 2 ( i ) E(\hat \theta - \theta)^2 \geq \frac{E^2[(\hat \theta - \theta)(\phi(Z) - E(\phi(Z))]}{E(\phi(Z) - E(\phi(Z))^2} \quad\quad\quad\quad (i) E(θ^−θ)2≥E(ϕ(Z)−E(ϕ(Z))2E2[(θ^−θ)(ϕ(Z)−E(ϕ(Z))](i)
可以看出来,上面式子其实已经有了克拉美罗下界的样子了,但是由于右边的式子与估计方法 \hat θ相关,因此右边的式子并不是真正的克拉美罗下界,我们要找的克拉美罗下界必须只依赖于模型本身,设计一个合适的φ消掉估计方法
我们引入一个参数△
f(z)是随机变量z的密度函数
ϕ ( Z ) = f ( z , θ + Δ ) f ( z , θ ) − 1 \phi(Z) = \frac{f(z,\theta + \Delta)}{f(z,\theta)} -1 ϕ(Z)=f(z,θ)f(z,θ+Δ)−1
求一下他的均值
E ( ϕ ( Z ) ) = ∫ − ∞ + ∞ ϕ ( Z ) ∗ f ( z , θ ) d z = ∫ − ∞ + ∞ ( f ( z , θ + Δ ) f ( z , θ ) − 1 ) ∗ f ( z , θ ) d z = ∫ − ∞ + ∞ ( f ( z , θ + Δ ) − f ( z , θ ) ) d z = 1 − 1 = 0 E(\phi(Z)) = \int_{-\infty}^{+\infty}\phi(Z)*f(z,\theta) dz \\ = \int_{-\infty}^{+\infty}(\frac{f(z,\theta + \Delta)}{f(z,\theta)} -1)*f(z,\theta) dz \\ =\int_{-\infty}^{+\infty}(f(z,\theta + \Delta)-f(z,\theta))dz \\ = 1-1 = 0 E(ϕ(Z))=∫−∞+∞ϕ(Z)∗f(z,θ)dz=∫−∞+∞(f(z,θ)f(z,θ+Δ)−1)∗f(z,θ)dz=∫−∞+∞(f(z,θ+Δ)−f(z,θ))dz=1−1=0
我们把函数φ代入原不等式
$$
E(\phi(Z) - E(\phi(Z))^2 = E\phi(Z) ^2 \quad\quad\quad\quad (ii)
$$
E 2 [ ( θ ^ − θ ) ( ϕ ( Z ) − E ( ϕ ( Z ) ) ] = E 2 ( θ ^ − θ ) ϕ ( Z ) = E 2 ( θ ^ ∗ ϕ ( Z ) ) + [ θ ∗ E ( ϕ ( Z ) ) ] 2 = E 2 ( θ ^ ( Z ) ∗ ϕ ( Z ) ) ( i i i ) E^2[(\hat \theta - \theta)(\phi(Z) - E(\phi(Z))] = E^2(\hat \theta - \theta)\phi(Z)\\ = E^2(\hat \theta*\phi(Z)) + [\theta*E(\phi(Z))]^2 =E^2(\hat \theta(Z)*\phi(Z))\quad\quad\quad\quad (iii) E2[(θ^−θ)(ϕ(Z)−E(ϕ(Z))]=E2(θ^−θ)ϕ(Z)=E2(θ^∗ϕ(Z))+[θ∗E(ϕ(Z))]2=E2(θ^(Z)∗ϕ(Z))(iii)
(iii)把φ(Z)进行代入
E
(
θ
^
(
Z
)
∗
ϕ
(
Z
)
)
=
∫
−
∞
+
∞
θ
^
(
Z
)
∗
ϕ
(
Z
)
∗
f
(
z
,
θ
)
d
z
=
∫
−
∞
+
∞
θ
^
(
Z
)
∗
(
f
(
z
,
θ
+
Δ
)
f
(
z
,
θ
)
−
1
)
∗
f
(
z
,
θ
)
d
z
=
∫
−
∞
+
∞
θ
^
(
Z
)
f
(
z
,
θ
+
Δ
)
d
z
−
∫
−
∞
+
∞
θ
^
(
Z
)
f
(
z
,
θ
)
d
z
E(\hat \theta(Z)*\phi(Z)) = \int_{-\infty}^{+\infty}\hat \theta(Z)*\phi(Z)*f(z,\theta) dz \\ = \int_{-\infty}^{+\infty}\hat \theta(Z)*(\frac{f(z,\theta + \Delta)}{f(z,\theta)}-1)*f(z,\theta) dz \\ = \int_{-\infty}^{+\infty}\hat \theta(Z)f(z,\theta + \Delta)dz - \int_{-\infty}^{+\infty}\hat \theta(Z)f(z,\theta )dz
E(θ^(Z)∗ϕ(Z))=∫−∞+∞θ^(Z)∗ϕ(Z)∗f(z,θ)dz=∫−∞+∞θ^(Z)∗(f(z,θ)f(z,θ+Δ)−1)∗f(z,θ)dz=∫−∞+∞θ^(Z)f(z,θ+Δ)dz−∫−∞+∞θ^(Z)f(z,θ)dz
因为是无偏估计,所以对 \hat θ求期望,其实就是括号里的那个估计量
∫ − ∞ + ∞ θ ^ ( Z ) f ( z , θ + Δ ) d z − ∫ − ∞ + ∞ θ ^ ( Z ) f ( z , θ ) d z = θ + Δ − θ = Δ \int_{-\infty}^{+\infty}\hat \theta(Z)f(z,\theta + \Delta)dz - \int_{-\infty}^{+\infty}\hat \theta(Z)f(z,\theta )dz = \theta + \Delta - \theta = \Delta ∫−∞+∞θ^(Z)f(z,θ+Δ)dz−∫−∞+∞θ^(Z)f(z,θ)dz=θ+Δ−θ=Δ
把(ii)和(iii)代入(i)
E ( θ ^ − θ ) 2 ≥ E 2 [ ( θ ^ − θ ) ( ϕ ( Z ) − E ( ϕ ( Z ) ) ] E ( ϕ ( Z ) − E ( ϕ ( Z ) ) 2 ≥ Δ 2 E ( f ( z , θ + Δ ) f ( z , θ ) − 1 ) 2 E(\hat \theta - \theta)^2 \geq \frac{E^2[(\hat \theta - \theta)(\phi(Z) - E(\phi(Z))]}{E(\phi(Z) - E(\phi(Z))^2} \\ \geq \frac{\Delta^2}{E(\frac{f(z,\theta + \Delta)}{f(z,\theta)}-1)^2} E(θ^−θ)2≥E(ϕ(Z)−E(ϕ(Z))2E2[(θ^−θ)(ϕ(Z)−E(ϕ(Z))]≥E(f(z,θ)f(z,θ+Δ)−1)2Δ2
令
Δ − > 0 \Delta ->0 Δ−>0
则
Δ 2 E ( f ( z , θ + Δ ) f ( z , θ ) − 1 ) 2 = 1 E [ f ( z , θ + Δ ) − f ( z , θ ) Δ ∗ 1 f ( z , θ ) ] 2 = 1 E [ ( ∂ ∂ θ f ( z , θ ) ) ∗ 1 f ( z , θ ) ] 2 = 1 E [ ( ∂ ∂ θ l n f ( z , θ ) ] 2 \frac{\Delta^2}{E(\frac{f(z,\theta + \Delta)}{f(z,\theta)}-1)^2} = \frac{1}{E[\frac{f(z,\theta + \Delta)-f(z,\theta)}{\Delta}*\frac{1}{f(z,\theta)}]^2} \\ = \frac{1}{E[(\frac{\partial}{\partial \theta }f(z,\theta))*\frac{1}{f(z,\theta)}]^2} = \frac{1}{E[(\frac{\partial}{\partial \theta }lnf(z,\theta)]^2} E(f(z,θ)f(z,θ+Δ)−1)2Δ2=E[Δf(z,θ+Δ)−f(z,θ)∗f(z,θ)1]21=E[(∂θ∂f(z,θ))∗f(z,θ)1]21=E[(∂θ∂lnf(z,θ)]21
可以证明克拉美罗下界
E ( θ ^ − θ ) 2 ≥ 1 E [ ( ∂ ∂ θ l n f ( z , θ ) ] 2 = I ( θ ) E(\hat \theta - \theta)^2 \geq \frac{1}{E[(\frac{\partial}{\partial \theta }lnf(z,\theta)]^2} = I(\theta) E(θ^−θ)2≥E[(∂θ∂lnf(z,θ)]21=I(θ)
3.4.4.4 克拉美罗下界的变形
(1) 证明
克拉美罗下界还有一种变形,用来分析θ有关的函数的下界,而不是θ本身
假设估计量的期望是g(θ)
E
(
θ
^
)
=
θ
,
E
(
θ
^
)
=
g
(
θ
)
E(\hat \theta) \cancel = \theta , E(\hat \theta) = g(\theta)
E(θ^)=
θ,E(θ^)=g(θ)
∫ − ∞ + ∞ f ( x , θ ) d x = 1 ∫ − ∞ + ∞ ∂ ∂ θ f ( x , θ ) d x = 0 ∫ − ∞ + ∞ [ ∂ ∂ θ l n f ( x , θ ) ] ∗ f ( x , θ ) d x = 0 \int_{-\infty}^{+\infty} f(x,\theta)dx = 1 \\ \int_{-\infty}^{+\infty} \frac{\partial}{\partial \theta }f(x,\theta)dx = 0 \\ \int_{-\infty}^{+\infty} [\frac{\partial}{\partial \theta }lnf(x,\theta)]* f(x,\theta)dx = 0 ∫−∞+∞f(x,θ)dx=1∫−∞+∞∂θ∂f(x,θ)dx=0∫−∞+∞[∂θ∂lnf(x,θ)]∗f(x,θ)dx=0
等式两边同时乘以g(θ)
∫ − ∞ + ∞ g ( θ ) ∗ [ ∂ ∂ θ l n f ( x , θ ) ] ∗ f ( x , θ ) d x = 0 ( i v ) \int_{-\infty}^{+\infty} g(\theta)*[\frac{\partial}{\partial \theta }lnf(x,\theta)]* f(x,\theta)dx = 0\quad\quad\quad\quad (iv) ∫−∞+∞g(θ)∗[∂θ∂lnf(x,θ)]∗f(x,θ)dx=0(iv)
因为g(θ)是期望,用期望的定义可得
g ( θ ) = ∫ − ∞ + ∞ θ ^ f ( x , θ ) d x g(\theta) = \int_{-\infty}^{+\infty} \hat \theta f(x,\theta)dx g(θ)=∫−∞+∞θ^f(x,θ)dx
求导数
g ′ ( θ ) = ∫ − ∞ + ∞ θ ^ ∂ ∂ θ f ( x , θ ) d x = ∫ − ∞ + ∞ θ ^ [ ∂ ∂ θ l n f ( x , θ ) ] ∗ f ( x , θ ) d x ( v ) g\prime(\theta) = \int_{-\infty}^{+\infty} \hat \theta \frac{\partial}{\partial \theta }f(x,\theta)dx \\ = \int_{-\infty}^{+\infty} \hat \theta [\frac{\partial}{\partial \theta }lnf(x,\theta)]* f(x,\theta)dx \quad\quad\quad\quad (v) g′(θ)=∫−∞+∞θ^∂θ∂f(x,θ)dx=∫−∞+∞θ^[∂θ∂lnf(x,θ)]∗f(x,θ)dx(v)
(v) - (iv) 得
∫
−
∞
+
∞
(
θ
^
−
g
(
θ
)
)
[
∂
∂
θ
l
n
f
(
x
,
θ
)
]
∗
f
(
x
,
θ
)
d
x
=
g
′
(
θ
)
∫
−
∞
+
∞
(
θ
^
−
g
(
θ
)
)
f
(
x
,
θ
)
[
∂
∂
θ
l
n
f
(
x
,
θ
)
]
∗
f
(
x
,
θ
)
d
x
=
g
′
(
θ
)
\int_{-\infty}^{+\infty} (\hat \theta-g(\theta) )[\frac{\partial}{\partial \theta }lnf(x,\theta)]* f(x,\theta)dx = g\prime(\theta) \\ \int_{-\infty}^{+\infty} (\hat \theta-g(\theta) )\sqrt{f(x,\theta)}[\frac{\partial}{\partial \theta }lnf(x,\theta)]* \sqrt{f(x,\theta)}dx = g\prime(\theta)
∫−∞+∞(θ^−g(θ))[∂θ∂lnf(x,θ)]∗f(x,θ)dx=g′(θ)∫−∞+∞(θ^−g(θ))f(x,θ)[∂θ∂lnf(x,θ)]∗f(x,θ)dx=g′(θ)
使用柯西不等式
[ ∫ − ∞ + ∞ ( θ ^ − g ( θ ) ) f ( x , θ ) [ ∂ ∂ θ l n f ( x , θ ) ] ∗ f ( x , θ ) d x ] 2 ≥ ∫ − ∞ + ∞ ( θ ^ − g ( θ ) ) 2 f ( x , θ ) d x ∗ ∫ − ∞ + ∞ [ ∂ ∂ θ l n f ( x , θ ) ] 2 f ( x , θ ) d x [\int_{-\infty}^{+\infty} (\hat \theta-g(\theta) )\sqrt{f(x,\theta)}[\frac{\partial}{\partial \theta }lnf(x,\theta)]* \sqrt{f(x,\theta)}dx ]^2 \geq \int_{-\infty}^{+\infty} (\hat \theta-g(\theta) )^2f(x,\theta)dx*\int_{-\infty}^{+\infty}[\frac{\partial}{\partial \theta }lnf(x,\theta)]^2f(x,\theta)dx [∫−∞+∞(θ^−g(θ))f(x,θ)[∂θ∂lnf(x,θ)]∗f(x,θ)dx]2≥∫−∞+∞(θ^−g(θ))2f(x,θ)dx∗∫−∞+∞[∂θ∂lnf(x,θ)]2f(x,θ)dx
即
∫ − ∞ + ∞ ( θ ^ − g ( θ ) ) 2 f ( x , θ ) d x ∗ ∫ − ∞ + ∞ [ ∂ ∂ θ l n f ( x , θ ) ] 2 f ( x , θ ) d x ≤ [ g ′ ( θ ) ] 2 \int_{-\infty}^{+\infty} (\hat \theta-g(\theta) )^2f(x,\theta)dx*\int_{-\infty}^{+\infty}[\frac{\partial}{\partial \theta }lnf(x,\theta)]^2f(x,\theta)dx \leq [g\prime(\theta)]^2 ∫−∞+∞(θ^−g(θ))2f(x,θ)dx∗∫−∞+∞[∂θ∂lnf(x,θ)]2f(x,θ)dx≤[g′(θ)]2
即
V a r ( θ ^ ) ≤ [ g ′ ( θ ) ] 2 I ( θ ) I ( θ ) = ∫ − ∞ + ∞ [ ∂ ∂ θ l n f ( x , θ ) ] 2 f ( x , θ ) d x Var(\hat \theta) \leq\frac{[g\prime(\theta)]^2}{ I(\theta)} \\ I(\theta) = \int_{-\infty}^{+\infty}[\frac{\partial}{\partial \theta }lnf(x,\theta)]^2f(x,\theta)dx Var(θ^)≤I(θ)[g′(θ)]2I(θ)=∫−∞+∞[∂θ∂lnf(x,θ)]2f(x,θ)dx
可以看出,当g(θ) = θ的时候,导数是1,就是通常情况下的克拉美罗下界
(2) 举例
假定采样数据Zk是两部分组成的,S是数据的一种形式,θ是估计量。N是符合高斯分布的噪声
Z k = S ( k , θ ) + N k N k ∼ n ( 0 , σ 2 ) , k = 1 , 2 , 3 , . . . , n Z_k = S(k,\theta) +N_k \\ N_k \sim n(0,\sigma^2),k = 1,2,3,...,n Zk=S(k,θ)+NkNk∼n(0,σ2),k=1,2,3,...,n
估计方法 \hat θ,我们来计算克拉美罗界和fisher信息量
θ ^ ( Z 1 , . . . , Z n ) = θ \hat \theta(Z_1,...,Z_n) = \theta θ^(Z1,...,Zn)=θ
计算克拉美罗界四部曲
- 第一步:写分布
分布是随机变量的联合分布
f ( Z 1 , . . . , Z n , θ ) = ( 1 2 π σ ) n e x p ( − 1 2 σ 2 ∑ k = 1 n ( Z k − S ( k , θ ) ) 2 ) f(Z_1,...,Z_n,\theta) = (\frac{1}{\sqrt{2\pi}\sigma})^n exp(-\frac{1}{2\sigma^2}\sum_{k=1}^n(Z_k-S(k,\theta))^2) f(Z1,...,Zn,θ)=(2πσ1)nexp(−2σ21k=1∑n(Zk−S(k,θ))2)
- 第二步:取ln
l n f ( Z 1 , . . . , Z n , θ ) = − n l n ( 2 π σ ) − 1 2 σ 2 ∑ k = 1 n ( Z k − S ( k , θ ) ) 2 lnf(Z_1,...,Z_n,\theta) = -nln(\sqrt{2\pi}\sigma) -\frac{1}{2\sigma^2}\sum_{k=1}^n(Z_k-S(k,\theta))^2 lnf(Z1,...,Zn,θ)=−nln(2πσ)−2σ21k=1∑n(Zk−S(k,θ))2
- 第三步:求二阶导数或者导数的平方
∂ ∂ θ l n f ( Z 1 , . . . , Z n , θ ) = 1 σ 2 ∑ k = 1 n ( Z k − S ( k , θ ) ) ∗ ∂ ∂ θ S ( k , θ ) \frac{\partial}{\partial \theta }lnf(Z_1,...,Z_n,\theta) = \frac{1}{\sigma^2} \sum_{k=1}^n(Z_k-S(k,\theta))*\frac{\partial}{\partial \theta }S(k,\theta) ∂θ∂lnf(Z1,...,Zn,θ)=σ21k=1∑n(Zk−S(k,θ))∗∂θ∂S(k,θ)
因为看起来求二阶导数并不好求,因此就求导数的平方了
- 第四步:求期望(fisher 信息量)
E
[
(
∂
∂
θ
l
n
f
(
Z
1
,
.
.
.
,
Z
n
,
θ
)
)
2
]
=
E
[
(
1
σ
2
∑
k
=
1
n
(
Z
k
−
S
(
k
,
θ
)
)
∗
∂
∂
θ
S
(
k
,
θ
)
)
2
]
(
a
)
E[(\frac{\partial}{\partial \theta }lnf(Z_1,...,Z_n,\theta))^2] = E[(\frac{1}{\sigma^2} \sum_{k=1}^n(Z_k-S(k,\theta))*\frac{\partial}{\partial \theta }S(k,\theta))^2] \quad\quad(a)
E[(∂θ∂lnf(Z1,...,Zn,θ))2]=E[(σ21k=1∑n(Zk−S(k,θ))∗∂θ∂S(k,θ))2](a)
对上面式子进行分析,有随机性的东西其实只有Zk,我们把无关常量分解出来
= 1 σ 4 E [ ( ∑ k = 1 n ( Z k − S ( k , θ ) ) ∗ ∂ ∂ θ S ( k , θ ) ) 2 ] = \frac{1}{\sigma^4}E[(\sum_{k=1}^n(Z_k-S(k,\theta))*\frac{\partial}{\partial \theta }S(k,\theta))^2] \\ =σ41E[(k=1∑n(Zk−S(k,θ))∗∂θ∂S(k,θ))2]
设
M ( i ) = ( Z i − S ( k , θ ) ) ∗ ∂ ∂ θ S ( i , θ ) ( b ′ ) M(i) = (Z_i-S(k,\theta))*\frac{\partial}{\partial \theta }S(i,\theta) \quad\quad(b\prime) M(i)=(Zi−S(k,θ))∗∂θ∂S(i,θ)(b′)
上式可以化简为
1 σ 4 E [ ( ∑ k = 1 n ( Z k − S ( k , θ ) ) ∗ ∂ ∂ θ S ( k , θ ) ) 2 ] = 1 σ 4 E ( ∑ k = 1 n M k 2 + ∑ j = j M i M j ) ( b ) \frac{1}{\sigma^4}E[(\sum_{k=1}^n(Z_k-S(k,\theta))*\frac{\partial}{\partial \theta }S(k,\theta))^2] = \frac{1}{\sigma^4}E(\sum_{k=1}^nM_k^2+\sum_{j\cancel= j}M_iM_j)\quad\quad(b) σ41E[(k=1∑n(Zk−S(k,θ))∗∂θ∂S(k,θ))2]=σ41E(k=1∑nMk2+j= j∑MiMj)(b)
因为变量都是独立同分布的,因此积的期望等于期望的积
E ( ∑ j = j M i M j ) = ∑ j = j E ( M i ) ∗ E ( M j ) E(\sum_{j\cancel= j}M_iM_j) = \sum_{j\cancel= j}E(M_i)*E(M_j) E(j= j∑MiMj)=j= j∑E(Mi)∗E(Mj)
因为
E ( M k ) = E ( Z k − S ( k , θ ) ) = E ( N k ) = 0 ( c ) E(M_k) = E(Z_k -S(k,\theta)) = E(N_k) = 0\quad\quad(c) E(Mk)=E(Zk−S(k,θ))=E(Nk)=0(c)
可知乘积的交叉项为0
把 c代入b中可得
1 σ 4 E ( ∑ k = 1 n M k 2 + ∑ j = j M i M j ) = 1 σ 4 E ( ∑ k = 1 n M k 2 ) ( d ) \frac{1}{\sigma^4}E(\sum_{k=1}^nM_k^2+\sum_{j\cancel= j}M_iM_j) = \frac{1}{\sigma^4}E(\sum_{k=1}^nM_k^2)\quad\quad(d) σ41E(k=1∑nMk2+j= j∑MiMj)=σ41E(k=1∑nMk2)(d)
把(d)和(b’)代入(a)中可得
1 σ 4 E [ ( ∑ k = 1 n ( Z k − S ( k , θ ) ) ∗ ∂ ∂ θ S ( k , θ ) ) 2 ] = 1 σ 4 E ( ∑ k = 1 n M k 2 ) = 1 σ 4 ∑ k = 1 n E [ ( Z k − S ( k , θ ) ) 2 ∗ ( ∂ ∂ θ S ( k , θ ) ) 2 ] = 1 σ 4 ∑ k = 1 n E [ ( Z k − S ( k , θ ) ) 2 ] ( ∂ ∂ θ S ( k , θ ) ) 2 ( e ) \frac{1}{\sigma^4}E[(\sum_{k=1}^n(Z_k-S(k,\theta))*\frac{\partial}{\partial \theta }S(k,\theta))^2] = \frac{1}{\sigma^4}E(\sum_{k=1}^nM_k^2) \\ = \frac{1}{\sigma^4}\sum_{k=1}^nE[ (Z_k-S(k,\theta))^2*(\frac{\partial}{\partial \theta }S(k,\theta))^2] = \frac{1}{\sigma^4}\sum_{k=1}^nE[ (Z_k-S(k,\theta))^2](\frac{\partial}{\partial \theta }S(k,\theta))^2 \quad\quad(e) σ41E[(k=1∑n(Zk−S(k,θ))∗∂θ∂S(k,θ))2]=σ41E(k=1∑nMk2)=σ41k=1∑nE[(Zk−S(k,θ))2∗(∂θ∂S(k,θ))2]=σ41k=1∑nE[(Zk−S(k,θ))2](∂θ∂S(k,θ))2(e)
根据已知量,我们可知
因为S没有随机性,所以求期望就是它本身
Z k = S ( k , θ ) + N k E ( Z k ) = E ( S ( k , θ ) + N k ) = E ( S ( k , θ ) ) + 0 = S ( k , θ ) V a r ( Z k ) = σ 2 Z_k =S(k,\theta)+N_k \\ E(Z_k) = E(S(k,\theta)+N_k) = E(S(k,\theta))+0 =S(k,\theta) \\ Var(Z_k) = \sigma^2 Zk=S(k,θ)+NkE(Zk)=E(S(k,θ)+Nk)=E(S(k,θ))+0=S(k,θ)Var(Zk)=σ2
因此有下式成立
E [ ( Z k − S ( k , θ ) ) 2 ] = E [ ( Z k − E ( Z k ) ) 2 ] = V a r ( Z k ) = σ 2 ( f ) E[ (Z_k-S(k,\theta))^2] = E[(Z_k - E(Z_k))^2] = Var(Z_k) = \sigma^2 \quad\quad(f) E[(Zk−S(k,θ))2]=E[(Zk−E(Zk))2]=Var(Zk)=σ2(f)
把(f)代入(e)中可得fisher信息量
1 σ 4 ∑ k = 1 n E [ ( Z k − S ( k , θ ) ) 2 ] ( ∂ ∂ θ S ( k , θ ) ) 2 = 1 σ 4 ∑ k = 1 n ( σ 2 ) ( ∂ ∂ θ S ( k , θ ) ) 2 = 1 σ 2 ∑ k = 1 n ( ∂ ∂ θ S ( k , θ ) ) 2 = I ( θ ) \frac{1}{\sigma^4}\sum_{k=1}^nE[ (Z_k-S(k,\theta))^2](\frac{\partial}{\partial \theta }S(k,\theta))^2 = \frac{1}{\sigma^4}\sum_{k=1}^n (\sigma^2)(\frac{\partial}{\partial \theta }S(k,\theta))^2 = \frac{1}{\sigma^2}\sum_{k=1}^n (\frac{\partial}{\partial \theta }S(k,\theta))^2 = I(\theta) σ41k=1∑nE[(Zk−S(k,θ))2](∂θ∂S(k,θ))2=σ41k=1∑n(σ2)(∂θ∂S(k,θ))2=σ21k=1∑n(∂θ∂S(k,θ))2=I(θ)
(3) 例子的在雷达信号估计中的具象化
这里我们举个具体的例子,假设是雷达信号的接收。我们把例子(2)认为是雷达接收的模型,我们来看看,到底什么影响雷达信号传递准确性。
首先是S(k,θ),我们认为S(k,θ)是雷达发射过来的信号的函数
S ( k , θ ) = S ( t − θ ) ∣ t = k Δ t = S ( k Δ t − θ ) S(k,\theta) = S(t- \theta)| _{t=k \Delta t} = S(k \Delta t - \theta) S(k,θ)=S(t−θ)∣t=kΔt=S(kΔt−θ)
S是时间t的函数,意义为时间为t的时候的信号大小。因为信号接收是有延时的,这里的θ就是信号的延时时间,也是我们要进行估计的值
对于这个模型的fisher统计量是
I
(
θ
)
=
1
σ
2
∑
k
=
1
n
(
∂
∂
θ
S
(
k
,
θ
)
)
2
=
1
σ
2
∑
k
=
1
n
(
∂
∂
θ
S
(
k
Δ
t
−
θ
)
)
2
I(\theta) = \frac{1}{\sigma^2}\sum_{k=1}^n (\frac{\partial}{\partial \theta }S(k,\theta))^2 = \frac{1}{\sigma^2}\sum_{k=1}^n (\frac{\partial}{\partial \theta }S(k\Delta t- \theta))^2
I(θ)=σ21k=1∑n(∂θ∂S(k,θ))2=σ21k=1∑n(∂θ∂S(kΔt−θ))2
我们来看看采集到的信号是什么样子的。假设第k的采样信号之前,雷达信号一直没有送到,所以接收到的都是早噪声。而第k+m个信号之后,信号发送完毕,后面采集到的信号也全部都是噪声
Z 1 = N 1 , Z 2 = N 2 , Z 3 = N 3 , . . . , Z k − 1 = N k − 1 , Z k = S ( 0 ) + N k , Z k + 1 = S ( 1 ) + N k + 1 , . . . , Z k + m = S ( m ) + N k + m , Z k + m + 1 = N k + m + 1 , . . . Z_1 = N_1, Z_2 = N_2, Z_3 = N_3,..., Z_{k-1} = N_{k-1} ,\\ Z_k = S(0)+N_k,Z_{k+1} = S(1) +N_{k+1},...,Z_{k+m} = S(m) +N_{k+m} , \\ Z_{k+m+1} = N_{k+m+1},... Z1=N1,Z2=N2,Z3=N3,...,Zk−1=Nk−1,Zk=S(0)+Nk,Zk+1=S(1)+Nk+1,...,Zk+m=S(m)+Nk+m,Zk+m+1=Nk+m+1,...
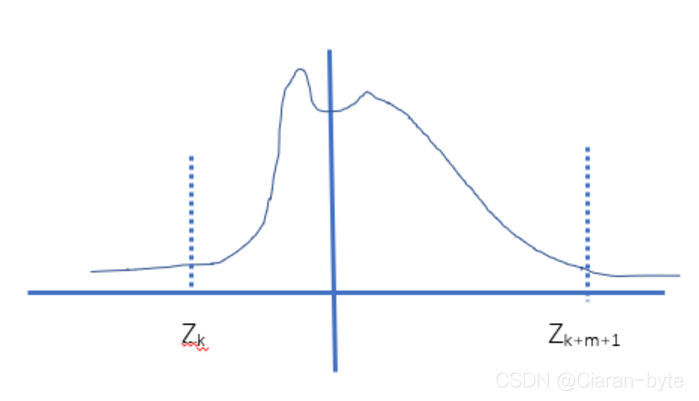
从图中可以看出
θ
=
k
∗
Δ
t
\theta = k*\Delta t
θ=k∗Δt
因为只有m个数据是有效的,我们去掉噪声点,计算fisher信息量
I ( θ ) = 1 σ 2 ∑ k = 1 m ( ∂ ∂ θ S ( θ ) ∣ θ = k Δ t ) 2 I(\theta) = \frac{1}{\sigma^2}\sum_{k=1}^m (\frac{\partial}{\partial \theta }S( \theta)|_{\theta = k \Delta t})^2 I(θ)=σ21k=1∑m(∂θ∂S(θ)∣θ=kΔt)2
I − 1 ( θ ) = Δ t 1 σ 2 ∑ k = 1 m ( ∂ ∂ θ S ( θ ) ∣ θ = k Δ t ) 2 ∗ Δ t I^{-1}(\theta) = \frac{\Delta t}{\frac{1}{\sigma^2}\sum_{k=1}^m (\frac{\partial}{\partial \theta }S( \theta)|_{\theta = k \Delta t})^2 *\Delta t} I−1(θ)=σ21∑k=1m(∂θ∂S(θ)∣θ=kΔt)2∗ΔtΔt
可以用积分对累加进行近似
I − 1 ( θ ) ≈ Δ t 1 σ 2 ∫ − ∞ + ∞ ( ∂ ∂ θ S ( θ ) ) 2 d θ I^{-1}(\theta) \approx \frac{\Delta t}{\frac{1}{\sigma^2}\int_{-\infty}^{+\infty}(\frac{\partial}{\partial \theta }S( \theta))^2d\theta} I−1(θ)≈σ21∫−∞+∞(∂θ∂S(θ))2dθΔt
这里的 △t其实就是采样间隔
采样间隔是带宽的倒数,我们可得
Δ t = 1 B \Delta t = \frac{1}{B} Δt=B1
Δ t 1 σ 2 ∫ − ∞ + ∞ ( ∂ ∂ θ S ( θ ) ) 2 d θ = 1 B 1 σ 2 ∫ − ∞ + ∞ ( ∂ ∂ θ S ( θ ) ) 2 d θ \frac{\Delta t}{\frac{1}{\sigma^2}\int_{-\infty}^{+\infty}(\frac{\partial}{\partial \theta }S( \theta))^2d\theta} = \frac{\frac{1}{B}}{\frac{1}{\sigma^2}\int_{-\infty}^{+\infty}(\frac{\partial}{\partial \theta }S( \theta))^2d\theta} σ21∫−∞+∞(∂θ∂S(θ))2dθΔt=σ21∫−∞+∞(∂θ∂S(θ))2dθB1
我们假设噪声是白噪声
白噪声的功率是 σ2,是功率密度和带宽之积
σ 2 = E ( N k 2 ) = N 0 ∗ B \sigma ^2 = E(N_k^2) = N_0*B σ2=E(Nk2)=N0∗B
代入上式得
I − 1 ( θ ) = N 0 ∫ − ∞ + ∞ ( ∂ ∂ θ S ( θ ) ) 2 d θ [ 1 ] I^{-1}(\theta) = \frac{N_0}{\int_{-\infty}^{+\infty}(\frac{\partial}{\partial \theta }S( \theta))^2d\theta}\quad\quad\quad\quad[1] I−1(θ)=∫−∞+∞(∂θ∂S(θ))2dθN0[1]
我们再引入傅里叶变换和帕塞瓦尔定律
定义符号\widetilde{S} 为S的傅里叶变换
S F ↔ S ~ S \quad \underleftrightarrow{\mathfrak{F}}\quad \widetilde{S} S FS
根据傅里叶变换的微分性质
∂ ∂ θ S ( θ ) F ↔ j ω S ~ [ 2 ] \frac{\partial}{\partial \theta }S(\theta) \quad \underleftrightarrow{\mathfrak{F}}\quad j\omega\widetilde{S}\quad\quad\quad\quad[2] ∂θ∂S(θ) FjωS [2]
根据帕塞瓦尔定理,时域积分的能量等于频域积分的能量
∫ − ∞ + ∞ ∣ S ( t ) ∣ 2 d t = 1 2 π ∫ − ∞ + ∞ ∣ S ( ω ) ~ ∣ d ω [ 3 ] \int_{-\infty}^{+\infty} |S(t)|^2 dt = \frac{1}{2 \pi}\int_{-\infty}^{+\infty}|\widetilde{S(\omega)}|d\omega\quad\quad\quad\quad[3] ∫−∞+∞∣S(t)∣2dt=2π1∫−∞+∞∣S(ω) ∣dω[3]
把[2]和[3]代入[1]中可得
I
−
1
(
θ
)
=
N
0
∫
−
∞
+
∞
(
∂
∂
θ
S
(
θ
)
)
2
d
θ
=
N
0
∫
−
∞
+
∞
∣
ω
∣
2
∣
S
(
ω
)
∣
2
~
d
ω
I^{-1}(\theta) = \frac{N_0}{\int_{-\infty}^{+\infty}(\frac{\partial}{\partial \theta }S( \theta))^2d\theta} = \frac{N_0}{\int_{-\infty}^{+\infty}|\omega|^2 |\widetilde{S(\omega)|^2}d \omega}
I−1(θ)=∫−∞+∞(∂θ∂S(θ))2dθN0=∫−∞+∞∣ω∣2∣S(ω)∣2
dωN0
有效带宽
∫ − ∞ + ∞ ∣ ω ∣ 2 ∣ S ( ω ) ∣ 2 ~ d ω = > E f f e c t i v e B a n d w i d t h \int_{-\infty}^{+\infty}|\omega|^2 |\widetilde{S(\omega)|^2}d \omega =>Effective \quad Bandwidth ∫−∞+∞∣ω∣2∣S(ω)∣2 dω=>EffectiveBandwidth
从而我们可以证明雷达原理中的知识:距离估计的精度取决于噪声的大小和信号的带宽
3.5 小结
首先我们要明确一个问题,我们这一小节一直在做的事情就是,评判和选择一个更好的估计方法(信号处理方法)。我们为什么要做估计?
这是因为,一般来说,我们通过采样能够得到一组采样数据,这组数据一般来说是独立同分布的。并且采样数据一般满足某种分布,这种分布规律是先验的,已知的。但是这个分布中有些参数我们是不知道的,因此,我们就需要利用采样得到的数据进行处理,然后基于我们的处理方法,得到分布函数中未知的参数,从而还原信号的原貌。可以说,估计是信号处理的结果。
那么我们应该找什么样的估计才是最好的呢?我们当然是希望找到最小误差的估计,尽可能还原参数的原貌。这个时候,我们会采用均方误差作为估计方法的评判手段。
但是随便一种方法都可以作为信号处理的手段,我们要宁缺毋滥,设置一个门槛,达到及格线的信号处理方法才能进入我们的眼球。因此我们把及格线设置为了,信号处理方法要求是无偏的。在估计方法是无偏的条件下,最小均方误差估计,就变成了最小方差无偏估计。
当我们找到及格了的信号处理方法以后,要做的就是对其进一步优化。Rao-blackwell 就是一种优化的过程。在现有的基础上,对估计进行改进。假设已经有了一个估计了,我们还有一个估计,是一个充分统计量,就可以形成一个新的估计,这个新估计的方差一定小于等于原来的方差。这就是Rao-blackwell 引理告诉我们的事情
在不断优化的过程中,我们还要不断的问自己,优化到最好了吗? 因为我们需要知道不断的改进是否是有尽头的,如果有尽头,他能够收敛到什么地步。通过完备统计量的方法,我们能确切的找到最小的方差 ,但是,完备统计量一般来说是不存在的。因此,我们退让了一步,找了克拉美罗下界作为优化的评判标准,如果最小方差无偏估计能够达到克拉美罗下界了,我们就认为这种估计方法已经足够完美了。






















 648
648











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








