【图像超分辨率】Satellite Image Super-Resolution via Multi-Scale Residual Deep Neural Network

摘要：

近来，卫星遥感图像的应用越来越普遍，但卫星传感器观测到的图像往往是低分辨率的，因此不能完全满足物体识别和分析的要求。为了充分利用遥感图像中物体的多尺度特征（multi-scale），本文提出了一种多尺度残差神经网络（MRNN）。MRNN采用卫星图像的多尺度特性，对超分辨率(SR)卫星图像准确重建高频信息。

1. 从超分辨率卫星图像中提取不同尺寸的块（patch），以适应不同尺度的物体。
2. 大、中、小尺度的深度残差神经网络被设计为模拟不同大小的感受野，以获取相对的全局、上下文和局部信息进行先验表示。
3. 然后，使用融合网络来完善不同尺度的信息。
4. MRNN将不同尺度网络的高频信息进行互补融合，重建出符合人类视觉经验的高分辨率卫星物体图像(“多尺度看更清楚”)。
   在SpaceNet卫星图像和NWPU-RESISC45数据库上的实验结果表明，所提出的方法在客观和主观图像质量方面优于几种最先进的SR算法。

1. 介绍：

从外层空间观测地面物体的遥感卫星被广泛用于各种实际应用，如环境监测、资源勘探、灾害预警和军事应用。由于受天基成像设备（电荷耦合器件（CCD）传感器）和通信带宽的限制，卫星观测到的图像一般分辨率较低。此外，卫星图像还受到大气湍流、传输噪声、运动模糊和光学传感器欠采样的影响。遥感卫星的图像质量和分辨率不能满足真实卫星图像分析的要求。超分辨率(SR)技术可以克服硬件限制，通过软件方式提高图像的空间分辨率。第一个SR算法[1]是通过融合多帧互补信息来提高Landsat遥感图像的分辨率。在过去的几十年中，SR已经成功地应用于提高遥感卫星图像的分辨率和质量。一个著名的例子是 SPOT-5，它通过对双 CCD 阵列按子像素采样间隔移动的两个 5 m 图像进行 SR 采样，达到 2.5 m 的分辨率[2,3]。传统的SR图像生成方法通常需要对同一场景进行多幅空间/光谱/时空低分辨率图像[4,5]。

现有的图像SR算法分为两类，即基于重建的算法和基于学习的算法[6]。基于重建的算法融合子像素LR多帧信息，重建其潜伏的高分辨率（HR）图像。以往的卫星SR方法利用基于重建的方法解决退化过程的反问题。基于重建的方法通过使用降采样、光学模糊、大气扰动、套准误差、几何变形和运动补偿等退化因子，用数学公式模拟成像的退化过程[7,8,9]。虽然基于重建的方法简单直观，并且可以灵活地与先验约束相结合，但它们依赖于精确的子像素精度估计。

受机器学习在物体识别等任务中取得的巨大成功的启发，基于学习的SR方法得到了高度重视，并成为研究的主流方向。它们的目的是通过训练数据集提供的先验信息来学习LR和HR图像/斑点之间的映射函数。与基于重建的方法相比，基于学习的SR算法可以获得更好的主观和客观重建性能，因为外部训练数据库提供了大量的先验信息。从先验训练样本的使用情况来看，基于学习的SR算法可以分为三类，即基于回归、表征和深度学习的算法。一些有代表性的基于回归的[10,11,12]和基于表征的SR算法[13,14,15]产生了不错的主观和客观性能。这些方法效率高，使用正则化项的框架灵活。

基于深度学习的方法为学习复杂的映射函数提供了端到端解决方案，并迅速成功地应用于SR任务。考虑到卷积神经网络（CNN）出色的学习能力，通过卷积神经网络（CNN）[16,17]学习LR和HR补丁之间复杂的非线性映射关系。Shi等[18]构建了一种亚像素CNN，提供了一种直接高效学习LR到HR图像的映射函数的新型方式，效率进一步提高。Kim等[19]指出，深度网络的构建可以有效缓解深度残差学习的训练难度。Lai等[20]构建了一个金字塔网络，用于融合特征域中的多尺度残差。由生成器和判别网络组成的生成式对抗网络（GAN）[21,22]用于生成假细节，以模拟良好的视觉输出。对于卫星图像，Luo等[23]用自相似性代替零填充，避免添加不可用信息，取得了良好的效果。Wang等[24]提出了一种用于视频SR的多内存CNN，以保留帧间时间相关性。

上述SR方法主要集中在一般自然图像上。而对于卫星图像，由于广域成像，图像中的物体尺度相对不同，在视觉任务中具有重要作用，如分割、特征提取、物体跟踪等。一些针对普通图像设计的深度学习算法，由于没有特别考虑卫星图像的多尺度特性，无法高效处理卫星图像。此外，足够的高频信息，如边缘和纹理，对于卫星图像检测[25]和物体识别[26,27,28,29,30]至关重要。在预测和重建物体时，如果不考虑物体的不同尺度，使用单一的结构网络会导致重建性能不佳。一个切实可行的解决方案是将多尺度信息探索到深度神经网络中。Zhang等[31]利用多尺度空间结构自相似性来学习多尺度字典。Fu等[32]利用图像的多尺度区域来训练循环注意网络，进行细粒度识别。Liu等[33]利用多尺度和多层次网络整体地获取层次化的边缘信息。与初始网络[34]类似，Du等[35]将三种不同尺度的滤波器的不同尺度特征进行融合。

上述基于CNN的SR模型构建了精细网络，并在学习重要的局部细节信息上推进了最先进的性能。[36]中的方法指出，过小的感受野导致缺乏足够的全局信息，无法产生良好的视觉效果。为了获得精细的局部细节信息，他们经常使用小的图像补丁进行训练（如SRCNN[17]、VDSR[19]、LapSRN[20]、SRResnet/SRGAN[21]）。在SR任务中，小的感受野只考虑有限的信息范围。这种模型缺乏获取SR的全局和上下文信息的能力。相反，Zeiler等人[37]可视化卷积网络表明，不同的网络层在表示模拟腹侧通路（ventral pathway）的特征以提高其性能方面具有不同的作用[38,39,40,41,42]。他们表示，不同尺度的分层特征能有效提高获取全局信息的能力。

受 “近看更好”[32]的启发，我们提出了一种灵活多用的卫星图像SR多尺度残差深度神经网络，命名为MRNN，用于卫星图像HR细节信息的分层重建。在该网络中，多尺度的感受野类似于人眼从不同距离的观察。我们对图像进行

1. 大尺度(大核大小的网络，用于全局信息)、
2. 中尺度(中核大小的网络，用于上下文信息)和
3. 小尺度(小核大小的网络，用于细微的局部信息)三个尺度的特征提取，
   以表示图像的多尺度信息。与传统的神经网络相比，MRNN融合的是残差信息而不是中间特征。因此，融合网络融合了所有尺度的残差信息，提高了高频细节。

本研究的贡献突出表现在以下几个方面。(一)提出了MRNN在卫星图像SR中的应用。提出的网络包含三个部分，即多尺度特征提取；并行的小尺度、中尺度和大尺度；残差融合网络。提出的多尺度神经网络在 "在多尺度中寻找更好的东西 "的基础上，充分利用了SR性能。(二)提出的残差增强网络和融合网络在SR任务中有效增强了卫星图像的高频信息。融合网络可以细化精细的边缘/细节纹理，从而改善卫星图像的细节。

本论文的其余部分组织如下。在第2节中，我们描述了所提出的方法的框架。在第三节中，我们对所提出的方法和一些有代表性的SR方法进行了比较。本研究的讨论和结论分别在第四节和第五节中给出。

2. 基于多尺度残余神经网络的卫星图像SR

我们利用图像显著性来显示不同尺寸图像之间的差异，强调多尺度图像的作用。**图像显著性[43]是图像中重要的视觉特征，强调人眼感知的区域的重要程度。**显著性图的亮度代表了物体部分的重要性。显著性地图S的公式为：

Iµ为平均图像特征向量， Iωhc (x, y)是原始图像的高斯模糊版（使用5 × 5 可分离二项式内核)中，在(x, y) 位置上对应的图像像素向量值。

图1显示了三种尺寸的图像补丁，即大尺寸-（91×91）、中尺寸-（61×61）和小尺寸-（41×41）图像补丁。在91×91图像补丁中，显著性地图(the saliency map)关注的是图像中的全局信息，如建筑物的轮廓。61×61图像补丁，其中包含了更多的上下文信息，显著性地图关注的是建筑部分和街道线条。对于41×41图像补丁，它的接受场很小，只观察局部信息，全局信息被忽略。在这里，可以回顾一下远距离的观测经验；当我们距离观测对象较远时，可以观测到全局的配置信息，如位置和外貌，而不包括细节信息。对于更多的细节，我们在接近时重点关注局部信息，如建筑物的装饰和颜色。这种观察方式很好地说明了多尺度信息在视觉观察中的作用。因此，仅在单尺度图像块（patch）上进行图像重建，不能同时有效地恢复物体的全局和局部信息。

图1.多尺寸图像补丁的显著性地图 多尺寸图像补丁的显著性地图。
(A)大尺度关注全局配置，如边缘位置；
(B)中尺度关注作为上下文信息的主体部分，如建筑部分；
©小尺度关注细节边缘和纹理。
显著性地图揭示了不同尺度的图像斑点在SR重建中的作用。不同大小的图像补丁有不同的特征表示方式。本实验符合人类的视觉经验(“多尺度看才能看得更清楚”)。大、中、小尺度网络用于模拟不同大小的感受野，以获取相对的全局、上下文和局部信息进行事先表示。

我们提出了一种新型的多尺度残差网络，其结构如图2所示。我们建立了三个具有不同尺度特征的自适应网络来预测其在不同尺度的卫星图像的高频残差信息。因此，我们利用残差融合网络，将不同尺度的残差图像合并其高频。由于残差图像中的像素值较小，我们利用Python Imaging Library的ImageEnhance模块https://github.com/python-pillow/Pillow，对图像进行增强对比度处理。增强后的图像blend_img由以下方式给出。

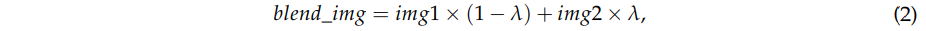
其中，img1 为原始图像，增强因子λ = 10 代表图像混合的权重。img2为生成图像，其像素值为0.5加上img1的平均值。λ越大，图像的对比度越大。

图2.MRNN的网络架构。MRNN的网络架构。该网络包括三个SR子网络和一个残差融合网络（k为卷积核大小；n表示卷积核数量；s表示步长大小）。残差块配置为两个多尺度内核的卷积层，然后是ReLU，以及一个跳转连接。. p = b(D − 2)/2c，其中|_|是x向下取整函数。当D为奇数时，我们在残差结构后面增加一个卷积层+ReLU。合并是指将图像补丁转换为图像。

对于一对训练数据集，其中LR图像（公式）和HR图像（公式），t为放大系数，i表示样本指数，M指训练样本数。将LR图像（公式）以双立方核插值到HR图像大小（公式），将训练数据集的张量版本重写为（公式）。上标代表网络类型，下标表示层数。上标K3、K5、K7、C、F分别代表K3-网络、K5-网络、K7-网络、Concat操作和残差融合网络。对不同大小的补丁进行抽样，导致每个规模的补丁数量不同。但是，所有的训练样本集都共享同一个训练集（公式）。图像补丁的数量计算如下。

其中*（公式） * 为底层函数，（公式） * 表示D层网络的接受场大小。图像补丁（公式） * 和*（公式） * 是根据*（公式） * 图像补丁的中心点获取的(详见图2)。将不同比例的LR和HR图像补丁对定义为*（公式） * 、（公式） * 和（公式） * ，它们的补丁尺寸分别为*（公式） * 、（公式） * 和（公式） * 像素，j为图像补丁的索引，（公式） * 、（公式） * 和*（公式） * 表示补丁的数量。考虑到残差融合，我们用补丁中心点来锚定三个不同大小的补丁，因此，（公式）。

2.1. 多尺度SR

我们使用三种不同尺度的网络来模拟不同深度的SR。网络深度分别为Dk3、Dk5和Dk7。参数D根据第3节的方法进行微调。在K3网络中，卷积滤波器定义为k=3。K3网络在补丁级的残差图定义如下。

其中fK3(xK3j)为预测的残差补丁，大小为41×41；WK320表示权重矩阵，大小为64×3×3×1；bK320表示偏置，大小为1×1；HK319表示通过激活ReLU生成的第19层的特征图，由64个特征图组成；j指图像补丁的索引。
对于K5-网络，其卷积核的大小为5×5像素。对于K7-网络，其滤波核大小为7×7像素。我们用同样的方法来计算输入图像补丁的大小。它们的残差图计算如下。

其中WK515的大小为64×5×5×1；WK715的大小为64×7×7×1；bK715和bK515的大小为1×1；j表示图像补丁的索引。HK514和HK714分别代表第14层的特征图，由K5-和K7-网络表示。

2.2. 剩余融合网络

为了实现不同尺度信息的互补，用大尺度信息描述对象的全局信息，而且，越看越近，层次细节越好。我们采用融合网络进行多尺度残差融合。

其中fK3(xK3j)r、fK5(xK5j)r和fK7(xK7j)r是三个不同尺度网络输出中去掉边界的残差图，fC(x)代表三层残差图的组合。Concat函数将多尺度残差图在第三维度上进行级联（连接三个时序）。无论输入x是否相同，K3-、K5-和K7-网络的输出都是不同的，因为它们通过自己的尺度重建残差信息。为了融合不同尺度的残差信息，我们使用一个简单的两层网络来融合三个通道信息。1×1卷积核是不同通道上每个像素的线性组合。1×1卷积核用于融合残差特征图。不同尺度的信息之间的跨通道信息交互，符合视觉认知的分层机制。我们可以得到最终的融合残差如下。

其中WF2为第二层权重矩阵，bF2表示其偏置，fC(x)表示输入的多尺度残差图，RF(x)表示最终融合的输出残差图。因此，最终的HR图像yˆ如下。

2.3. 损失功能

我们定义了以均方误差（MSE）为目标函数的损失函数。在MRNN中，我们将总体损失函数表述如下。

其中前三个项是多尺度残差网络(K3-、K5-和K7-网络)的损失。最后一项代表残差融合损失。我们简单设置α=β=χ=δ=1。我们使用两步法来训练网络。最初，我们用不同比例的补丁并行训练三个SR网络。然后，我们根据接触到的残图确定第二次的融合损失。
采用梯度下降法通过反向传播来优化网络参数。卷积操作可以减小特征图的大小。我们通过垫零（padding zero）的方式保持许多边缘像素，以准确推断中心像素，并保证所有特征图的大小相同，以保留图像补丁边缘的信息。

3. 实验

3.1. 实验数据

基于学习的超分辨率方法从训练数据提供的先验信息中学习LR图像的缺失高频信息。一般来说，训练数据越多，SR方法可以获得的重建效果越好。此外，SR重建方法的性能还与测试图像与训练图像的相似度有关。如果测试图像与训练图像的统计特征接近，则更容易获得良好的重建效果。此时，为了得到好的结果，可能会减少训练样本的数量。相反，当测试图像和训练图像的统计特征相差很大时，即使使用大规模的训练集也很难得到满意的结果。为了验证MRNN的性能，我们在SpaceNet图像和NWPU-RESISC45这两个卫星图像数据集上进行了实验，以保证所有算法使用相同数量的训练数据。SpaceNet卫星图像数据集https://spacenetchallenge.github.io/AOI_Lists/AOI_1_Rio.html，包括里约热内卢、巴黎、拉斯维加斯、上海和喀土穆五个地区，这些数据集是从DigitalGlobe的WorldView-2卫星上采集的，并在亚马逊公开发布。里约热内卢完整的卫星影像（空间分辨率为0.5米），影像分辨率最高，为2.8M×2.6M像素，分为6540个不重叠的HR影像斑块， 436 × 404像素，影像中感兴趣的主要内容为建筑物和道路。从这些图像补丁中随机选取建筑物图像共2080张，其中2000张、40张、40张图像分别作为训练集、验证集和测试样本。

NWPU-RESISC45数据集http://pan.baidu.com/s/1mifR6tU[44]是西北工业大学(NWPU)创建的一个公开的遥感图像场景分类(RESISC)基准。这个数据集涵盖了45个类，每个类中有700张图像。我们从每个类中随机选取52张图像，其中50张用于训练，其余用于测试。HR图像大小为 256 × 256 像素。NWPU-RESISC45的空间分辨率从大约30米到0.2米不等[44]。与SpaceNet数据集相比，NWPU-RESISC45数据集中的图像具有复杂和不稳定的成像条件，包括各种天气、季节和照明条件。这些因素给SR方法带来了巨大的困难。

图像退化是一个非常复杂的过程，需要通过一些滤波器和下采样算子来建模。在目前的工作中(例如我们工作中的所有对比方法[17,20,21,23,45])，最常用的图像退化是双立方体下采样。由于基于学习的超分辨率算法会学习低分辨率和高分辨率图像之间的映射关系，所以双立方降维是最公平的比较方法。复杂的成像退化模型将在未来的研究中进行研究。在测试过程中，图像不需要进行分割。

峰值信噪比(PSNR)和结构相似度(SSIM)描述了重建图像和原始图像之间的相似度。最近的研究表明，特征相似度（FSIM）和**视觉信息保真度（VIF）**与主观结果进一步一致。矩形归一化超像素熵指数(RSEI)https://github.com/jiaming-wang/RSEI，通过引入图像的空间结构，获得进一步准确的图像评价结果。互信息(MI)可以用信息来表示图像之间的信息依赖程度。MI分值越高，依赖度越大，图像之间的相似度越高。补丁y和yˆ之间的相互信息定义如下。

其中q和g代表灰度值，P(g)表示灰度值为g的像素数与增加图像的比值，P(q,g)是q和g的联合分布函数。
我们将SR图像yˆ和LR图像x相对于HR图像y之间的信息增益定义如下。

所有的图像质量评估指标只考虑YCbCr色彩空间的Y分量。

3.2. 训练参数

所提出的网络是一个端到端网络，每个子网络必须训练80个epochs作为前期训练网络。整个网络的训练时间为10个epochs。

考虑到深度网络层，算法采用了学习率衰减的方法。我们遵循Kim等人[19]设置超参数：学习率初始化为0.1，学习率每20个纪元降低1/10，网络的动量为0.9。为了避免过度拟合，我们使用了正则化的ℓ2-norm，其权重衰减为0.0001。对于K3-残差学习网络，我们将步长设置为1，填充大小为1；对于K5-网络，步长等于1，填充大小为2；对于K7-网络，我们将步长设置为1，填充大小为3。我们应用MSRA方法[50]来初始化权重，即满足均值为0的高斯分布，利用方差为√2/n (n is the batch size)（n为批次大小），并利用一个常数来初始化偏置项，初始值为0。我们最初将RGB图像转换为YCbCr颜色空间，然后重建Y通道。重建后，将Y通道图像恢复到RGB色彩空间。我们使用Caffe库[51]实现了MRNN模型。用4个1080Ti GPU训练MRNN大概需要10小时。

3.3. 多尺度残差的互补性分析

如果不同尺度残差信息之间的重合度较低，则意味着不同尺度之间残差信息的互补性较好[52]。因此，在本节中，我们展示了不同尺度上残差信息的分布情况。我们从SpaceNet图像数据集中选取了15幅具有代表性的LR图像{xi}(i=1,…,15)和相应的HR图像{yi}，配置与3.6节相同。多尺度网络的重建残差图为{fj(xi)}(j=K3,K5,K7)，共45幅残差图像。估计残差误差图定义为ermji=fj(xi)-(yi-xi)(i=1,…,15andj=K3,K5,K7)，我们通过主成分分析(PCA)将其投影到3D和2D残差特征空间中，如图3所示。2D和3D特征空间的分布图显示，多尺度网络提供的估计残差误差不同。这一观察也证明了它们是互补的。图3B中观察到的重叠覆盖了一个足够大的特征空间，即使只使用三个平行网络。因此，额外的并行网络只会增加重叠度。

图3. (A,B)分别是3D和2D特征空间中估计残差误差图分布的可视化。蓝色点代表来自K3网络的残差，绿色和红色点分别代表K5-和K7-网络。

图3中的分布图无法清晰描述多尺度残差的互补模式。因此，我们通过k-means对数据实施聚类，得到它们在二维特征空间的分布，如图4所示。我们将这四种模式命名为 “s+m+l”、“s+m/l”、"m+s/l "和 “l+s/m”。模式 "s+m+l "代表了最好的情况，即三个尺度的高频信息在任意两个尺度之间是互补的。后三种模式可分为：两个尺度的信息相当共同，但也存在互补关系，而另一个尺度则对它们进行互补。这种行为有效地证明了多尺度残差之间的互补性。

图4.多尺度残图的互补模式。多尺度残图的互补模式。(A) "s+m+l "表示 “s+m+l”。小-中-大面积残差互为补充；（B）"s+m/l "代表的是 表示小尺度的残余信息与中尺度和大尺度的残余信息都是互补的。© "m+s/l "是指中尺度残余信息与小尺度和大尺度残余信息互补； (D) "m+s/l "是指中尺度残余信息与小尺度和大尺度残余信息互补。(D) "l+s/m "代表了大尺度残余信息的模式。与中小规模的相辅相成。

定量验证如下所示：

其中abs(.)以元素的方式表示矩阵的绝对值。函数card(.)可以统计矩阵中非零元素的个数。Cermj表示数值大于阈值t的元素数，Coverlap表示三个误差残差图中相同位置的上述元素数。我们参考Wang等[52]，设t=9代表高值分量（高频信息信号）。图5绘制了柱状图。蓝色条形图代表只来自K3-网络的误差，绿色和红色条形图分别代表只来自K5-和K7-网络的误差。Coverlap为紫色条形。∀j∈{K3,k5,k7},Coverlap<Cermj,不同尺度的网络在所提出的方法中发挥着不同的作用。

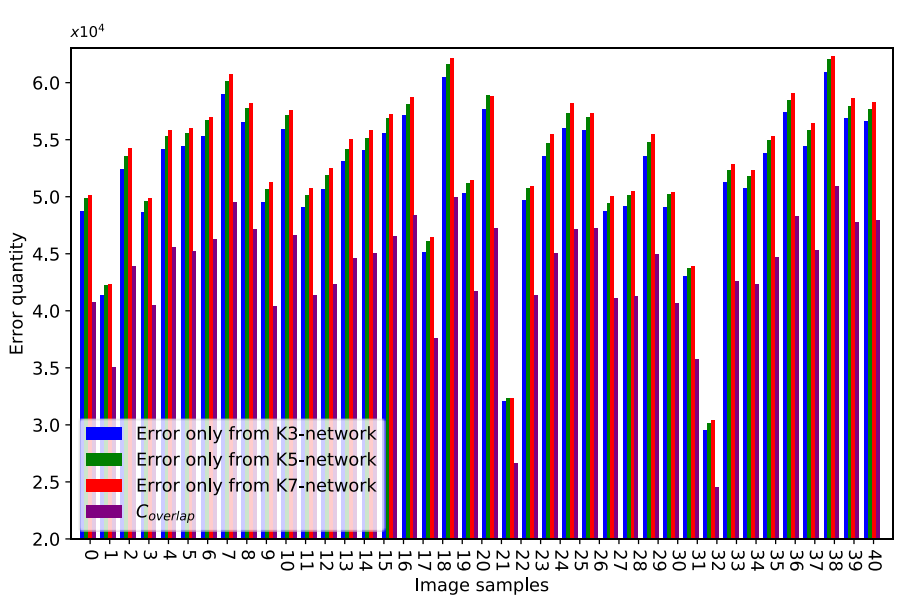
图5.来自多尺度残差的估计误差量。来自多尺度的估计误差数量多于重叠。请放大以查看差异

统计数据和定性评估证明，多尺度网络学习的高频信息是互补的。这种情况是我们融合多尺度残差图以提高重建性能的原因。

3.4. 性能和模型权衡

我们将多尺度残差网络配置成不同的深度，并对其性能进行比较。我们将D设置为5、10、15、20和25来测试网络性能。当网络深度发生变化时，输入图像补丁大小发生变化。我们使用PSNR来衡量网络性能，如图6所示。对于K3-网络，当D为20时，性能最佳。对于K5-和K7-网络，当D为15时，网络的性能为最佳。D层网络的接受场SD×SD定义为SD=(k-1)×D+1，k为内核大小。

3.5. 可视化学习的过滤器和特征图

上一节介绍的实验表明，三种不同深度的未知节点类型：字体网络可以替代MRNN。结果证明，在某些低级视觉任务中，“更深并不是更好”。我们希望K5-和K7-网络能够学习上下文和全局信息，以弥补K3-网络中信息的不足。因此，我们将网络可视化，以考虑本节中不同规模网络的作用。
在识别任务中，网络学习到的特征呈现出层次化的特征。深层特征比浅层特征，如颜色和边缘，更有辨别力。因此，水平可视化适合描述从低到高的识别过程。图像还原与识别任务不同。为了探索不同尺度网络的作用，我们对MRNN进行纵向可视化，即不同尺度网络倒数第二层的滤波器和特征图。
从过滤器中观察到模式的复杂性有很大的差异。图7表示了特征图。滤波器越大，特征图中表示的局部细节信息越少。滤波器越小，特征图中的细节信息越明显。

图7.最后一层但比例系数为4的特征图的可视化。最后一层特征图的可视化，比例系数为4。 K3-（前两行）、K5-（第三和第四行）和K7-网络（最后两行）的特征图。小尺寸的过滤器从特征图中传输了相当多的局部细节信息。此外，第一行比第二行和第三行有更丰富的细节，这可以看作是SR的细粒度网络。第三行边缘模糊，包含粗粒度的全局信息。第二行是上下文信息的中粒网络。

3.6. 与最先进的SR算法的性能比较

我们使用PSNR、SSIM、FSIM、VIF、RSEI和GMI对重建的图像进行了主观的定性和定量分析。
为了验证我们算法的有效性，我们将MRNN与以下最先进的SR算法进行了比较。

• SelfExSR[45]是基于自相似性的SR，是性能最好的算法。
• SRCNN[17]是一种经典的基于深度学习的方法，它首先使用CNN进行SR任务。
• LapSRN[20]是最著名的基于深度学习的多尺度SR算法。
• VISR[23]是通过CNN实现卫星图像SR算法中性能最好的一种。
• SRResnet[21]是一种计算效率高、视觉保真度高的优秀深度网络算法。

这些算法都是使用它们的公共源代码和作者提供的可用参数来实现的，所有图像都是通过使用MATLAB相同的双立方核进行下采样的。为了公平的比较，我们训练所有这些算法与相同的数据库配置，并评估了相同的卫星图像与建议的网络。
图8显示了所有40幅测试图像的PSNR，SSIM，FSIM，VIF，RSEI和GMI。MRNN获得了改进的重建结果。对应的显著性水平分别为100%、100%、97.5%、100%、100%和95%。MRNN与其他方法的得分差异有统计学意义。表1和表2显示，与基于深度学习的前沿算法相比，所提出的方法在数量上具有相当大的优势。这一发现表明，残差多尺度网络在学习不同尺度的内容和结构方面是比较有效的，它们通过使用比竞争算法所使用的更深、更扁平的网络来恢复图像信息的有效性。

图8.SR算法在SpaceNet卫星图像上的客观结果。SR算法在SpaceNet卫星图像上的客观结果。X轴表示测试样本的指数。Y轴表示评价指数。PSNR、SSIM、FSIM、VIF、RSEI和GMI。

表1. PSNR、SSIM、MI和GMI在SpaceNet数据集上的平均结果，比例因子为4，粗体表示性能最好。

表2. NWPU-RESISC45数据集上PSNR、SSIM、MI和GMI的平均结果，比例因子为4，粗体表示性能最好。

为了进行简单的观察，我们在随机选取的重建图像中放大了具有代表性的尺度对象进行对比。如图9所示，我们选择了屋顶（小尺度物体）、建筑物（中尺度物体）和街角（大尺度物体）来展示SR的性能。对于图9中所示的例子，我们的方法比其他方法在所有物体尺度上都能产生更锐利的边缘和更精细的细节。此外，我们的方法比LapSRN在所有物体尺度上都产生了更锐利的边缘和更精细的细节。这个条件证实了MRNN融合了多尺度的残差信息来提升视觉性能。图10显示了另一个直观的结果，即只有我们的方法可以恢复清晰的轮廓。

图9.不同SR算法在SpaceNet卫星图像上的主观性能。不同SR算法在SpaceNet卫星图像上的主观性能。我们选取了三个具有代表性尺度的物体，即屋顶(小尺度物体)、建筑物(中尺度物体)和街角(大尺度物体)，MRNN恢复的纹理信息更多。

图10.NWPU-RESISC45的图像，比例系数为4×。来自NWPU-RESISC45的图像，比例系数为4×。只有MRNN成功恢复了飞机头部的边缘。在MRNN的结果中，图像中的轮廓很清晰。

3.7. 时间复杂度

图11显示了所有算法的运行时间。传统算法的运行时间比深度学习算法的运行时间长，而且没有训练阶段。MRNN是一个具有三种不同尺度的并行网络，不会增加网络的时间复杂度，特别是当网络复杂时。虽然LapSRN具有更好的运行时间性能，但其PSNR低于MRNN。我们的方法在运行时间上比VISR稍慢。然而，MRNN的PSNR、SSIM、FSIM、VIF、RSEI和GMI都有所提高。我们在实验中，在相同的硬件配置下实现了所有算法。Intel Core i7-6700 K CPU @4.00 GHz, NVIDIA GTX1080 8 GB RAM.

4. 讨论情况

4.1. 多尺度事先信息

Lai等人[20]提出了一种渐进式SR方法，逐步实现图像的超分辨率。在SR的生成网络中采用了Laplacian金字塔。采用残差递归网络来预测每个金字塔级别的输出信息。在这里，LapSRN设计了一种多尺度的训练策略，将多尺度的组合训练成2×、4×、8×在一张网中。这个过程涉及到增加多尺度训练对以覆盖不同尺度的样本。在LapSRN和MRNN之间存在许多差异。首先，LapSRN直接在特征域进行多尺度信息融合，而**MRNN构建多尺度并行网络，在残差域进行多尺度信息融合。**残差图与图像的高频信息密切相关，这正是SR的目的。其次，LapSRN可以执行不同尺度因子一射的SR任务，但它忽略了输入图像中的多尺度信息。MRNN在固定尺度因子下的SR中完全考察了输入图像的多尺度信息。根据实验结果，在尺度因子为4时，多尺度残差信息的融合性能优于LapSRN。

4.2. 残差学习与像素学习的比较

VISR[23]使用自相似填充代替零填充，以避免增加不必要的信息。因此，VISR是在像素域进行的，如SRCNN。在像素域中的重建主要关注图像中的中低频信息。但是，SR可以推导出缺失的高频信息。此外，图像的残差值经常很小或为零，残差网络的计算负担始终低于像素学习。恢复卫星图像的高频信息可以提高识别性能。在这一点上，残差学习进一步适用于卫星图像SR场景。此外，实验结果也从主观和客观图像质量方面证实了这一推论。

4.3. 子像素网络与像素网络的对比

SRResnet[21]直接将LR图像划分为小的图像斑块。与LapSRN和ESPNN[18]类似，这些网络直接使用LR输入（子像素）来学习映射函数。子像素网络模拟了退化过程，比基于像素的网络效率更高。相比之下，像素网络将LR输入插值到相同大小的HR样本中，并使用网络中的残差信息。残差递归网络被认为可以克服消失问题，以提高网络性能。因此，子像素和像素网络有各自的优势。根据SpaceNet数据库中的实验数据，像素网络的性能优于子像素竞争对手。

4.4. 所提方法的适用性

我们在吉林一号卫星图像上进行了实验，以进一步说明所提出算法的适用性。测试图像的成像环境和分辨率与训练数据集（NWPU-RESISC45）不同。LR吉林一号卫星影像的大小为408×204像素。图12显示了我们提出的方法和对比方法得到的重建结果。考虑到没有地面真像，我们引入平均梯度（MG）来计算SR图像的清晰度。MG的定义如下。

其中，grdx(y) and grdy(y) 分别是图像y在x轴和y轴上的梯度。所提出的MRNN能够恢复锐利的边缘，并享有第一的MG分数。真实视频卫星图像的对比结果表明了所提出方法的适用性。考虑到卫星之间的图像特征，我们引入GAN来学习跨域退化模型，用于解决未来的实际SR问题。

5. 结论

本文根据卫星图像的特点，提出了一种多尺度残差CNN，即MRNN，用于提高SR性能。它首先从LR卫星图像中提取不同大小的块patch，然后应用多尺度的深度残差神经网络模拟不同大小的接收点，以提高SR性能。本文根据卫星图像的特点，首先从LR卫星图像中提取不同大小的斑点，然后应用多尺度深度残差神经网络模拟不同大小的接收场，以获取不同层次的信息。然后，采用融合网络对多尺度特征进行细化。基于所提出的新型网络，通过补充不同尺度的残差信息，可以得到合理准确的高频信息，如边缘和纹理等。在SpaceNet数据库上的实验结果表明，提出的MRNN有效地增强了重建图像中的高频信息。MRNN还表现出比几种最先进的基于深度学习的卫星图像SR算法更好的主观和客观图像质量。MRNN主要是针对真彩色卫星图像SR设计的。众所周知，多光谱图像具有较高的光谱分辨率，但空间分辨率较低。在所提出的框架中研究多光谱图像和真彩色图像的融合，以提高未来多光谱图像的可视化质量，将是非常有趣的。