Compressor aerodynamics, by Cumpsty学习笔记，第一章

觅°

已于 2023-06-18 09:48:51 修改

阅读量940

点赞数 1

文章标签：学习笔记

于 2023-06-11 20:35:50 首次发布

本文链接：https://blog.csdn.net/qq_41817886/article/details/131028941

版权

1 Useful basic ideas

1.1 简介：本章将介绍一些基本思想

1.2 叶片与流动

在叶轮机械领域，流动是所有叶片排共同作用的结果，任何一个叶片本身的影响是比较小的。设计叶片或叶片排可以视为选择一个与所需要流动相匹配的结构。

落后角的定义：叶片出口气流角（flow angle）与叶片出口金属角（blade angle）之间的差称为落后角

$\delta =\alpha _{2}-\chi _{2}$

落后角主要受无粘效应影响，边界层流动对其影响是相对较小的。对于轴流式压气机而言，落后角大约为

$\delta =0.3\theta \sqrt{s/c}$

其中 $\theta$ 为弯角（camber angle），s是叶片周向间距，c是弦长，因此落后角主要与弯角以及稠度相关。出口流动角主要与叶片安装角（stagger angle）相关，而受弯角影响相对较小，然而在高马赫数来流情况下，这一结论不再正确。尽管如此，叶片安装角在高马赫数来流情况下仍然是一个重要影响因素，因为其对叶片通流面积和通流能力有着直接的影响。

由于压气机内存在转子和静子，二者的相对运动导致流动是非定常的，这使得流动变得极为复杂。为简化流动，通常假设流动定常，在静子处采用绝对静止坐标系，在转子处采用相对旋转坐标系。流动参考坐标系的转换可用速度三角形来描述

通常进口轴向速度并不等于出口轴向速度，但二者一般相差不大，因此作等于的简化并不影响分析速度变化趋势。

1.3 做功

如下图所示，流体以 $V_{\theta 1}$ 在r1处流入，以 $V_{\theta2}$ 在r2处流出

若质量流量为m kg/s，则产生此变化所需要的扭矩为

$T=m(r_{2}V_{\theta2}-r_1V_{\theta1})$

对单位质量流体所做功为

$W=\omega (r_2V_{\theta2}-r_1V_{\theta1})$

此即为欧拉功

$W=U_2V_{\theta2}-U_1V_{\theta1}$

在一些特殊情况下，如存在机匣处理时，端壁处会产生不可忽视的切应力，此时欧拉公式可能误差过大。在这种情况下，扭矩可由局部叶片力和半径计算

$rF_{\theta}=m\delta (rV_{\theta})$

$rF_{\theta}=\rho VA\frac{\partial rV_{\theta}}{\partial s} \delta s$

$rf_{\theta}=V \frac{\partial rV_{\theta}}{\partial s}$

在定常情况下

$rf_{\theta}=\frac{D(rV_{\theta})}{Dt}$

其中 $f_{\theta}$ 是单位质量流体的的切向受力。

从能量方程出发

$h_{02}-h_{01}=Q+W$

绝热时Q=0，上式可以写作

$h_2+\frac{V_2^2}{2}-U_2V_{\theta2}=h_1+\frac{V_1^2}{2}-U_1V_{\theta1}$

等价为

$h_2+\frac{W_2^2}{2}-\frac{U_2^2}{2}=h_1+\frac{W_1^2}{2}-\frac{U_1^2}{2}$

定义转子焓为 $I=h+\frac{V^2}{2}-\frac{U^2}{2}$ ，因此有

$I_2=I_1$

在相对旋转坐标系下，转焓守恒的条件是

1）在相对旋转坐标系下流动定常；

2）在相对旋转坐标系下对流体无做功；

3）流动绝热。

相对旋转坐标系下转焓的概念可以类比绝对静止坐标系下滞止焓的概念。

压气机的目标是提升气体的静压，按照热力学关系式 $dh=dp/ \rho +Tds$ ，静压提升静焓会提升，其中s表示熵值。当流动熵增为0，也就是无损失时，压缩过程为等熵压缩，如下图所示，出口静压为p2s，若存在损失，则出口压强p2会低于等熵压缩出口压强p2s。

损失主要与剪切力（也就是粘性耗散）以及流动掺混相关。静焓变化为

$h_2-h_1=\frac{1}{2}(W_1^2-W_2^2)+\frac{1}{2}(U_2^2-U_1^2)$

损失倾向于与相对流动的减速相关，也就是与右式第一项 $\frac{1}{2}(W_1^2-W_2^2)$ 相关，而不是与静焓总体变化h2-h1相关。因此由右式第二项 $\frac{1}{2}(U_2^2-U_1^2)$ 所导致的静焓升（也就是压升）是等熵的，也就是无损失的。在气动上，通过提升 $\frac{1}{2}(U_2^2-U_1^2)$ 来提高压升是无限制的，但是通过降低相对速度是有限制的——相对速度下降过度，会发生流动分离。事实上，提高叶片速度也是有限制的，但限制在于叶片材料强度上，而非气动上。

流动径向位置的变化（也就是 $\frac{1}{2}(U_2^2-U_1^2)$ 的提高）在轴流式压气机里也有着显著影响。利用流动径向位置提升来提高压升在轴流压气机叶根处尤为明显，如下图所示，图（a）的结构就很好的利用了这一无损失增压原理，而图（b）则没有发挥这一优势。

经推导可以获得

$\frac{Dh_0}{Dt}=\frac{1}{\rho}\frac{\partial p}{\partial t}$

一个流体质点沿流线的滞止焓的变化率等于该流体质点静压的瞬时变化率。因此只有在非定常情况下滞止焓才会发生变化。该公式表示叶轮机械内的流动不可能是定常的。即便如此，欧拉公式，以及采用静止和相对旋转坐标系分别作为静子和转子的参考坐标系，以将流动假设为定常的方法，依旧得到了广泛应用。

1.4 Dynamic scaling

1）几何

最常见的无量纲几何因子包括稠度（弦长/周向间距）、展弦比（平均叶片长度/平均叶片弦长）、轮毂轮盖半径比。

采用什么参数对几何进行缩放一直没有定论，如对叶顶间隙，当采用不同流动模型时利用叶高、弦长、周向间距、安装间距或叶顶截面叶片最大厚度对叶顶间隙进行缩放的结果不同。

2）总体气动参数

用户对压气机最关心的参数包括质量流量、压比、转速和效率。

对压力，可采用进口总压p01作为分母，选择出口静压p2作为分子，当压气机出口气流流入另一个压气机，或者直接用于产生推力时，也可选用出口总压p02作为分子。

$\frac{p_2}{p_{01}} or \frac{p_{02}}{p_{01}}$

3 ）压气机速度

$\frac{U}{\sqrt{\gamma RT_{01}}}$

其中U为叶尖速度，T01为压气机进口总温。对同一台机器（rtip不变），并假设气体 $\gamma R$ 为常数，也可以采用以下无量纲量表示压气机速度

$N_{corr}=\frac{N}{\sqrt{T_{01}/T_{0ref}}}$

其中N为转速， $T_{0ref}$ 为参考总温。

4 ）质量流量

$\frac{m}{m_{stall}}$

mstall为失速时的质量流量，上式与以下因子成比例

$\frac{m\sqrt{RT_{01}}}{Ap_{01}} or \frac{m\sqrt{Cp T_{01}}}{Ap_{01}}$

A为通流面积，当A与R不变时

$m_{corr}=m\frac{\sqrt{\theta}}{\delta}, \theta=\frac{T_{01}}{T_{0ref}}, \delta=\frac{p_{01}}{p_{0ref}}$

对于一个结构固定（如无可调静叶）的压气机，其总体性能参数可以写作

$\frac{p_{02}}{p_{01}}=f(\frac{m\sqrt{T_0}}{p_0}, \frac{N}{\sqrt{T_0}})$

气动参数

1）级和叶片负荷

负荷系数 $\psi =\frac{\Delta h}{U^2}$

压升系数 $\psi =\frac{\Delta p}{\rho U^2}$

2）流量系数

$\phi =\frac{V_x}{U}$

轴向速度Vx可以取当地值，也可以取通流截面的平均值。流量系数决定了流入角（incidence），因此对压气机性能有着重要影响。对于轴流压气机，流量系数通常在0.3-0.9.

3）雷诺数

$Re=\frac{VL}{\nu }$

在叶轮机械中，雷诺数通常为 $10^5$ 或更大的数量级。对轴流压气机，可选择叶片弦长作为特征长度，进口相对速度作为特征速度，并选择叶片上游粘度作为特征粘度。当Re低于一定数值时，损失随着Re的降低而迅速增加。对于粗糙叶片而言，当Re达到一定数值时，损失与Re的相关性变差，此时损失主要由叶片表面粗糙度决定。

1.5 损失

采用质量平均总压来描述损失

$\bar{p_0}=\frac{\int p_0 \rho Vdy}{\int \rho V dy}$

损失来源：

a. 固体表面的摩擦力

只考虑摩擦力对损失的影响，最好的方法时考虑不可压缩气体通过平直叶栅时所产生的损失，如下图所示

来流V1, p1均匀，出口速度v2不均匀，在下游V3再次均匀。由于流动是不可压缩的，因此V1=V3，且

$V_1s=V_3s=\int v_2dy=V_2(s-\delta^*), \delta^*=\int_0^s(1-\frac{v}{V})dy$

$\delta^*$ 为每个通道叶栅表面的流动总位移厚度。在平面1和3处应用动量守恒定律

$\left [ F+(p_3-p_1)s \right ]\Delta t=mV_3-mV_1$

F是叶栅表面的摩擦力。由于mV3=mV1，因此

$Fs=p_1-p_3$

静压和总压存在一定关系，因此Fs与总压降成正比。通过以上分析可知，获得叶片表面摩擦力，即可获得摩擦总压损失，这一结论可以拓展至可压缩流动。但不要被上述例子误导，动量位移厚度并不是与损失最相关的变量。

b. 掺混损失

掺混的本质特征是流动的非均匀性。需要注意区分会导致掺混损失的流动非均匀性和不会导致掺混损失的流动分均匀性，如，叶片导致的非均匀流以产生升力，如果叶片设计良好，则不太会导致掺混损失，而如果叶片设计不好或出于非设计流动状态，流动存在大规模分离区，则会导致不可忽略的掺混损失。

随着马赫数的增大，叶片远下游的掺混损失/叶片出口损失逐渐增大。

c. 激波损失

当流动通过单个正激波减速时损失最大，如果可以通过一系列斜激波减速，则该过程可接近可逆过程。压气机进口马赫数大于1.4的情况是很少见的，在这种情况下，通过一个正激波所产生的总压降仅占进口总压的4.2%，其产生的静压升为2.1，因此通过正激波增压是非常有效的。设计超音速叶片的一个目标是保证叶片进口下游的马赫数不至于过高。在一些情况下，进口下游的马赫数可升至1.6。激波损失与(M-1)^3成正比，因此M的稍微增加都会导致损失的急速上升。

激波会导致边界层分离。如果边界层可以再附着，那么损失还不至于过大，但如果导致了大范围分离区，那么损失将是十分可观的。

d. 剪切力做功损耗

速度梯度很大时需要考虑剪切力做功损失，包括在边界层，尾迹，分离区以及regions dividing fast(?)。如下图所示，考虑一个边界层内流动，法向剪切力远远小于流向剪切力，因此动量方程可写为

$\rho V\frac{\partial V}{\partial x}=\frac{\partial \tau }{\partial y}-\frac{\partial p}{\partial x}$

能量方程可以写作

$\rho V\frac{\partial h_0}{\partial x}=\frac{\mu}{Pr}\frac{\partial ^2}{\partial y^2}(h_0+(Pr-1)\frac{V^2}{2})$

一般情况下，Pr可取为1，且进口总焓均匀，因此在绝热端壁上，沿边界层总焓守恒。考虑热力学关系式 $Tds=dh-dp/\rho$ ，与上面两式联立可得

$T\frac{\partial s}{\partial x}=-\frac{1}{\rho}\frac{\partial \tau }{\partial y}$

在定常情况下写为物质导数形式

$T\frac{Ds}{Dt}=-\frac{V\partial \tau }{\rho\partial y}$

扩展为三维形式

$T\frac{\partial s}{\partial t}=-\frac{V_i}{\rho} \frac{\partial \tau _{ij}}{\partial x_j}$

剪切力不是完全有害的，例如，边界层外侧的剪切力是为边界层内流动提供动量以克服逆压梯度的来源。

e. 宏观损失

考虑一个二维叶栅

对总压损失进行积分

$\int _{area}\rho v_2(p_{01}-p_{02})dA$

定义能量位移厚度

$\delta_3=\int_0^s\frac{v_2}{V_2}[(1-(\frac{v_2}{V_2})^2)]dy$

动量厚度

$\theta =\int v/V(1-v/V)dy$

形状因子

$H=\frac{\delta^*}{\theta}$

$\delta^*$ 为位移厚度。Lieblein测量了叶栅下游形状因子变化，如下图所示

测量损失至少要在叶栅下游三分之一弦长位置处测量。在叶轮机械内损失测量通常十分靠近叶片尾缘。Lieblein推荐采用以下公式计算非失速状态下叶栅的质量平均总压损失

$\omega_1=2\frac{\theta}{c}\frac{\sigma}{cos\alpha_2}[\frac{cos\alpha_1}{cos\alpha_2}]^2$

1.6 效率

当理想压气机的压升和真实压气机的压升相等时，定义效率为

$\eta =$ (work into ideal compressor)/(work into actual compressor)

对于出口气流直接用于推动、加热或燃烧的情况，理想压气机内流动为绝热和可逆的，此时为等熵压缩，等熵效率为

$\eta_{isen}=\frac{W_{s-constant}}{W_{actual}}$

绝热意味着输入的功等于滞止焓升 $W=h_{02}-h_{01}$ ，忽视滞止焓和静焓的差别，W=h2-h1，因此

$\eta_{is}=\frac{h_{2s}-h_1}{h_2-h_1}$

对于理想（ideal）气体而言

$h=CpT$

$\frac{p}{\rho}=RT$

当气体为完全（perfect）气体时，Cp为常数。当气体压强较低时，理想气体假设满足，但在许多压气机内部气体严重偏离理想状态。衡量气体偏离理想状态的程度可以用压缩因子

$Z=\frac{pv}{RT}$

实际气体通用压缩因子图

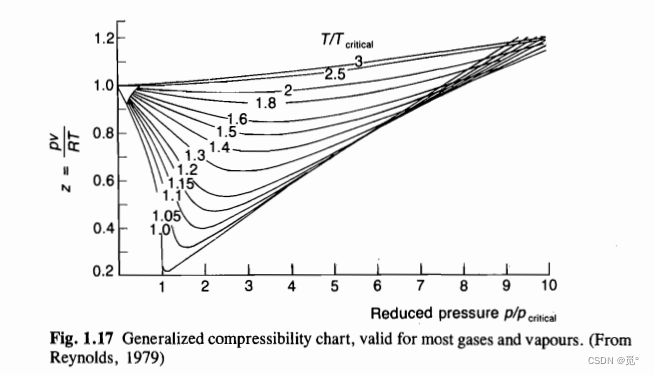
理想气体压缩因子图应为一条z=1的水平直线。幸运的是通常气体压缩都处于T/Tcri=2~5之间，因此做理想气体的假设不会偏离实际过多。在此范围内空气的cp=1.003~1.066kJ/(kgK), $\gamma$ =1.401~1.368，变化小，可以做常数假设。然而，对于总压比在40：1附近的压气机，有必要考虑cp和 $\gamma$ 的变化。对于制冷剂、碳氢化合物等，也需要考虑cp和 $\gamma$ 的变化。在压气机气动设计领域，通常基于理想气体假设，而在整机领域，则需要考虑实际气体偏差。

对于理想气体

$\frac{T_{2s}}{T_1}=(\frac{p_2}{p_1})^{\frac{\gamma -1}{\gamma}}$

因此

$\eta_{is} =\frac{(p_2/p_1)^{(\gamma-1)/\gamma}-1}{T_2/T_1-1}$

下图展示了一个等熵可逆压缩和不可逆压缩的T-s图

在T-s图上，等压线的斜率等于温度，因此当初始温度越高，产生一定压升的所需温升越高。在多级压气机内，后面级要产生和前面级同样的压升，所需做功更多。

多变效率：假设在一个有限压升过程中多变效率是常数

$\frac{T_2}{T_1}=(\frac{p_2}{p_1})^{(\gamma-1)/(\eta_p\gamma)}$

$\eta_p=\frac{\gamma-1}{\gamma}\frac{ln(p_2/p_1)}{ln(T_2/T_1)}$

可得

$\eta_{is}=\frac{(p_2/p_1)^{(\gamma-1)/\gamma}-1}{(p_2/p_1)^{(\gamma-1)/(\eta_p\gamma)}-1}$

当压升p2/p1增大时，等熵效率和绝热效率之间的差值会增大。当压升增大时，理想气体与实际气体之间的差异也会增大。

多级压气机的每一级对整机压比和整机效率的贡献不同。提高后面级的级多变效率对整机压比和整机等熵效率的提升程度大于提高前面级的级多变效率。

觅°

关注

1
点赞
踩
6

收藏

觉得还不错? 一键收藏
0
评论
Compressor aerodynamics, by Cumpsty学习笔记，第一章

压气机进口马赫数大于1.4的情况是很少见的，在这种情况下，通过一个正激波所产生的总压降仅占进口总压的4.2%，其产生的静压升为2.1，因此通过正激波增压是非常有效的。需要注意区分会导致掺混损失的流动非均匀性和不会导致掺混损失的流动分均匀性，如，叶片导致的非均匀流以产生升力，如果叶片设计良好，则不太会导致掺混损失，而如果叶片设计不好或出于非设计流动状态，流动存在大规模分离区，则会导致不可忽略的掺混损失。在叶轮机械领域，流动是所有叶片排共同作用的结果，任何一个叶片本身的影响是比较小的。激波会导致边界层分离。
复制链接

扫一扫