机器人运动学---可操作性

机器人运动学—可操作性

1. 引言

1.1 伪逆应用

对于操作空间维度是6的机器人而言，其求雅克比逆矩阵方法如下：

• 无冗余的情况：机器人操作空间维度 = 机器人关节数，此时雅克比矩阵是 6×6 ，求关节角速度方法如下：
  $$\dot{q}=J^{-1}(q)v_e$$

• 冗余的情况：机器人操作空间维度 < 机器人关节数，比如7自由度机械臂雅克比矩阵是 6×7 的，此时应该用右伪逆来计算关节角速度：
  $$\dot{q}=J^T(J{J}^T{)}^{-1}{v}_e$$

• 欠驱动情况：机器人操作空间维度 > 机器人关节数，比如一个4自由度的SCARA机械臂雅克比矩阵是 6×4 的。此时应该用左伪逆来计算关节角速度：
  $$\dot{q}=(J^{T}J{)}^{-1}{J}^T{v}_e$$

• SVD奇异值分解求逆 - 涉及阻尼最小二乘法

• Modern Robotics逆运动学数值解法及SVD算法

• 矩阵奇异值分解（SVD）

2 可操作性

2.1 奇异位形

当机器人处于某种状态时会造成机器人末端执行器丧失若干个运动自由度，如下图，当两个连杆都伸直时，机器人都是沿 x 轴方向上的自由度。

2.2 可操作性的表达

在机器人接近奇异位形时也同样会存在关节速度突增等种种我们不希望出现的情况。因此很多时候我们不只需要关心机器人是否奇异还希望定量的去判断机器人当前距离奇异位形究竟有多远。可操作性就是衡量机器人与奇异位形的距离的一种度量方式。
为了衡量在某个位形下机器人末端在各个自由度方向可以有多大的运动能力，我们取一个单位角速度向量作为关节速度的输入，即：
$${\dot{q}}^T\dot{q}=1$$

从几何上说，上述方程描述的是高维空间中的球面。把伪逆代入，得到：
$$v_e^T(J^{†T}(q)J^{†}(q))v_e=1$$

对于冗余机械臂也就是：
$$v_e^T(J(q)J^T(q){)}^{-1}{v}_e=1$$

可以看到这个方程描述的是高维空间的椭球面，椭球面（二维情况下是椭圆）的形状和方向由其二次型的核（也就是 $(J(q)J^T(q){)}^{-1}$） 决定，等价于考察$J{J}^T$。椭球体的主轴方向由矩阵$J{J}^T$的特征向量$u_i,i=1,\dots ,r$确定，而轴的尺度由$J$的奇异值${\sigma }_i=\sqrt{{\lambda }_i(J{J}^T)}(i=1,\dots ,r)$给出。

为了能够更直观的度量机器人与奇异位形之间的距离，可以使用$J{J}^T$的行列式（与椭球体容积成比例）来作为机械手运动能力的度量。
$$\omega (q)=\sqrt{det(J{J}^T)}$$

当机械臂处于奇异位形时，$J{J}^T$不是满秩的，必然存在零特征值，因此$\omega =0$。在非奇异位置$\omega >0$。因此称为机械臂可操作性度量。它描述了机械臂与奇异位形之间的距离。

关节角速度取的是单位值，那么如果它引起的末端某个自由度方向比较大的速度，说明机器人在当前位形下在这个自由度方向上具有很大的运动能力。相反当它引起的末端某个自由度方向极小的速度，说明机器人在这个方向上具备很低的运动能力，如果需要机器人在这个自由度方向产生比较大的速度那么必定导致非常大的关节角速度。

对于二连杆平面臂而言$v_e=\left(\begin{array}{cc}\dot{x}& \dot{y}\end{array}\right)$，$(J(q)J^T(q){)}^{-1}=\left(\begin{array}{cc}{k}_1& k_2\\ k_3& k_4\end{array}\right)$，那么$v_e^T(J(q)J^T(q){)}^{-1}{v}_e=1$可以展开成：
$k_1{\dot{x}}^2+(k_2+k_3)\dot{x}\dot{y}+k_4{\dot{y}}^2=1$

这是一个典型的半正定二次型，对应的几何形状是椭圆。由于雅克比矩阵与机器人当前构型相关，因此椭圆的形状在不同的关节角度处是不一样的，而从椭圆中心到椭圆边界的向量长度描述的则是机器人在这个自由度方向的运动能力。如下图所示。

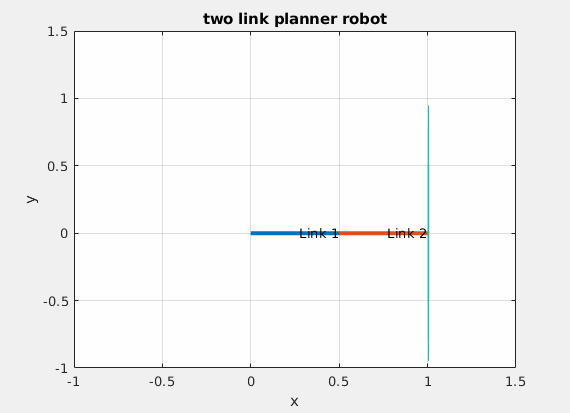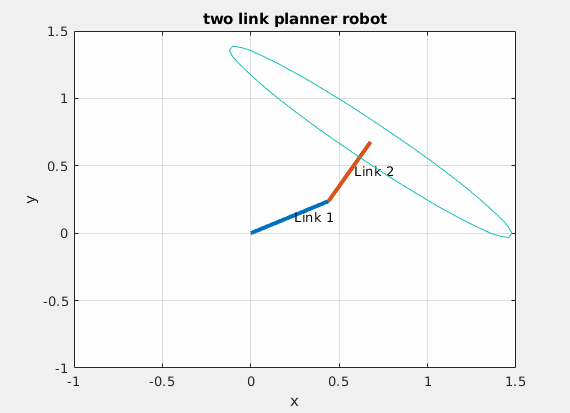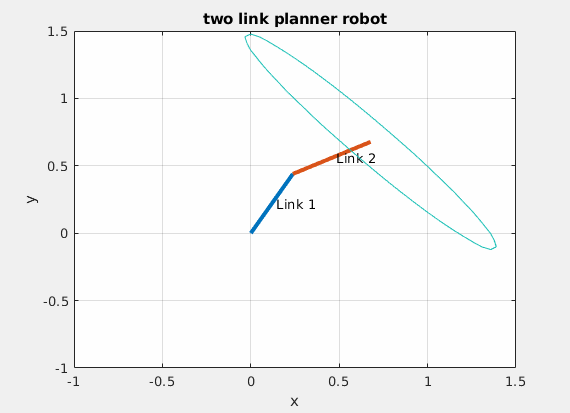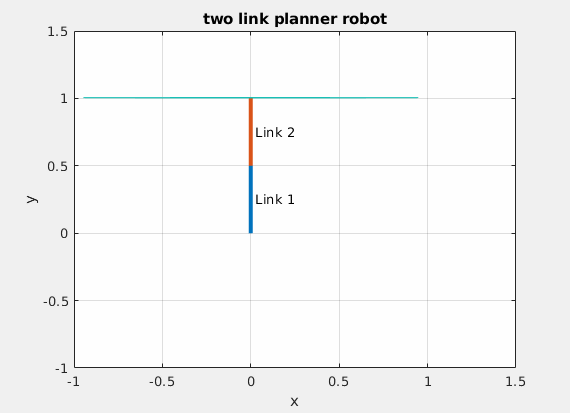
可操作性椭球

椭圆越扁说明在其短轴方向机器人的运动能力越差，在奇异位置处可操作性椭球收缩为一条直线。
二连杆平面臂的可操作性求解与可视化相关代码见github: https://github.com/hitgavin/simmechanics/tree/master/two_link_planner_robot

3 不可逆矩阵的求逆

比较经典的解决方案是所谓的渐消最小二乘方法（阻尼最小二乘法）即将伪逆表达为以下等式：
　　$$J^{\ast }=J^T(J{J}^T+\lambda I{)}^{-1}$$
其中$\lambda$是大于零的一个渐消因子，它通常比较小。比如在进行二连杆平面臂可操作性仿真编程时有如下代码：

% jacobian matrix
J = [-y1, y1 - y2; 
     x1 , x2 - x1];
J = inv(J*J' + eye(2)*0.0001);

你可以看一下最后一行的求逆过程，eye(2)*0.0001对应的就是$\lambda I$。

本文参考文档均以超链接形式在文中给出。
以上内容根据自己理解和实践所写，如有错误，请批评指正。