算法设计 第十一章 近似算法

---

1 近似算法

存在一些难解的问题，不能有效的找到最优解，如何做？降低标准，寻找足够优的解。
优化中的常见现象，将问题松弛或者将非凸问题转为凸问题，等等。降低求解复杂度，找到一个最够优的解。

1.1 近似率：

X是一个极大化问题，A是求解X的算法。$x_A$是算法A求出的解，$x_{\ast }$是最优解。
如果A的解至少是$\frac{1}{a}$的最优解，$x_A\ge \frac{1}{\alpha }{x}_{\ast }$，则A是$\alpha$-近似算法。
对于极小化问题，$x_A\le \alpha x_{\ast }$。

2例子

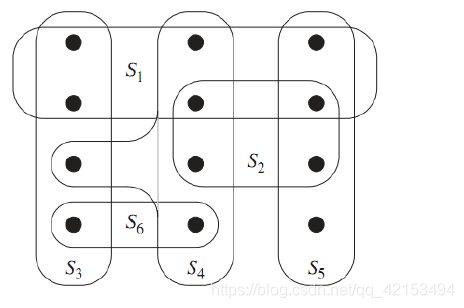
2.1集合覆盖 set cover

给定集合的集合 F = { S 1 , . . . , S n } F=\{S_1,...,S_n\} F={S1​,...,Sn​}，$\cup S_i=X$，每个集合$S_i$有对应的成本，我们希望找到$F$的子集，覆盖所有元素。每个$S_i$的成本相同，本质希望找到最少的子集来覆盖所有元素。

2.1.1 贪婪近似算法

当我们选择一个集合之后，删除已经被覆盖的元素。然后我们选择每个单位成本最小的集合直到覆盖所有元素。本质上每次选择覆盖未覆盖元素最多的集合。

• $U=X$
• $C=$
• whille U$\ne$ {}
  – $S\in F-C$ with min $cost(S)/|S\cap U|$
  – $C=C\cup S$
  – $U=U-S$
• output $C$

2.1.2 计算近似率

选择的集合按照先后顺序为$S_1,S_2,\dots ,S_m$。
$n_i$是选择$S_i$时，其覆盖的新元素个数。
元素被覆盖的顺序$e_1,e_2,\dots ,e_n$。
设$S_j$第一次覆盖新元素$e_k$。
$C_1,...$是最优覆盖中的部分集合，覆盖了$e_k,\dots ,e_n$。$n_i^{\prime }$是其覆盖的对应元素个数。不仅仅是$e_k,\dots ,e_n$中的元素。

• 1 ${\sum }_i{n}_i^{\prime }\ge n-k+1$, ${\sum }_{i}cost(C_i)\le OPT$因为$C_i,...$也可能覆盖了其他元素，是从最优覆盖中选择的部分集合。
• 2 $C_1,....$没有与$S_1,...S_{j-1}$重复的。假设某个$C_i$在$S_1,...S_{j-1}$中，则$e_k$之后的元素会被某个$S_i（i\in [1,j-1]）$覆盖，矛盾。
• 3 ${\sum }_{i}cost(C_i)/{\sum }_i{n}_i^{\prime }\le OPT/(n-k+1)$==>存在某个$cost(C_i)/n_i^{\prime }\le OPT/(n-k+1)$。
• 4 $cost(S_j)/n_j$贪婪算法选出的，所以$cost(S_j)/n_j\le cost(C_i)/n_i^{\prime }$(有个问题这里的$n^{\prime }$不是覆盖的新元素个数,$\le$未必成立啊？？)
• 对于每个k都存在满足3和4的$C_i$
• ${\sum }_{k}cost(e_k)\le {\sum }_{k}cost(C_i)/n_i^{\prime }\le {\sum }_{k}OPT/(n-k+1)\sim ln(n)\ast opt$。

2.2 时序问题 scheduling

n个独立的工作，m个处理器，给每个处理器分配任务，使得完成时间最早。

2.2.1 近似算法一

将工作任意排序，然后分配任务给每个处理器，优先分配给该时刻没有任务的处理器。

2.2.2 近似率

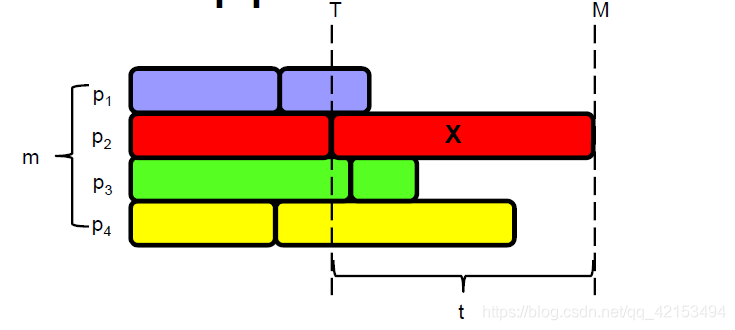
假设最优的makespan的$M^{\ast }$。

• $M^{\ast }\ge t$ 因为要完成工作$X$
• $M^{\ast }>T$ 因为T时刻之前的工作是满的。
• $M^{\ast }>max(T,t)$
• $M=T+t\le 2M^{\ast }$

2.2.3 近似算法二

按照工作时间长短排序，工作时间长则优先处理。makespan 是$M$

2.2.4 近似率二

$M=t+T\le t+M^{\ast }$

• if $t\le M^{\ast }/3$,==>$M\le 4M^{\ast }/3$
• if $t>M^{\ast }/3$则所有任务的尺寸不小于$M^{\ast }/3$,最优算法时每个处理器最多处理两个任务，此时该算法返回最优解。

算法一是online 可以实时操作，算法二需要知道所有任务的尺寸。

2.3背包问题 knapsack

2.4 点集覆盖 vertex cover

G(V,E) 找到一个V的子集覆盖所有边E。尽可能选择最少的点。

2.4.1 近似算法

思路：找到一个最优的边集覆盖。

• 选择E中的任意一边$(u,v)$
• $u,v$是我们选择的边。
• 移除所有与$u,v$连接的点。如下图所示：
  

2.4.2近似率

该算法是2-近似，设$C^{\ast }$是最优解。$A$是近似算法选出的边。注意这里是边，不是点。
$C=2\ast |A|\le 2\ast |C^{\ast }|$

2.5 旅行商问题 TSP

• 输入一个完全图
• 输出最小的距离的环，经过所有的点。
• 假设符合三角不等式。

2.5.1 近似算法1

• 最小生出树$T$
• 访问树中所有节点，允许重复$T^{\prime }$
• 跳过重复的节点$H$
• 

2.5.2 近似率

设最优解为$H^{\ast }$
因为$T$是最小生成树,$c(T)\le C(H^{\ast })$。
T经过所有点两次$c(T^{\ast })=2c(T)$。
因为$H$是$T^{\ast }$经过shortcut之后的,$c(H)\le c(T^{\ast })$。
总是$c(H)\le c(T^{\prime })=2c(T)\le 2c(H^{\ast })$。

2.5.3 近似算法2

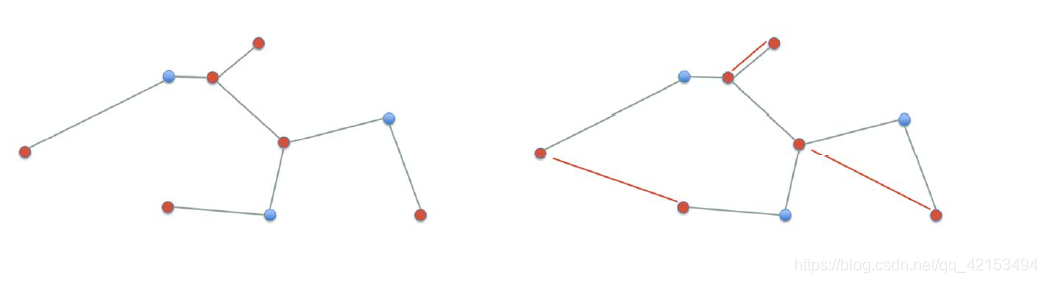
Euler tour：访问图中的所有边一次，当且仅当所有的点有偶数度。

• 最小生成树T

• 找到奇数度的点V’

• 构造最小的，完美匹配（一个点只与一个点相连）M

• 

• 将M添加到T中获得T’,所有的点都是偶数度。

• 得到T’的 Euler tour T’’

• shortcut T’’ 去获得H

2.5.4

H’是V’(奇数度点)的最优TSP
最小完美匹配M，因为每个点只有一个match，而且是最小的，$H^{\prime }$有两个match，$c(M)\le c(H^{\prime })/2\le c(H^{\ast })/2$
$c(H)\le c(T^{\ast })=c(M)+c(T)\le c(H^{\ast })/2+c(H^{\ast })$

2.6k-center 问题

n个sites 我们想建立k个中心来服务他们，每个site选择离它最近的中心。
我们想要极小化最大的服务距离。

2.6.1算法

选择site作为中心
每次选择里中心最远的site作为中心。

2.6.2 近似率

$r=ma{x}_{S}mi{n}_{C}d(s,c)$
这里有k+1个点距离不小于$r$，k个中心，以及剩下一个到中心最大距离的site。
假设$r>2r^{\ast }$

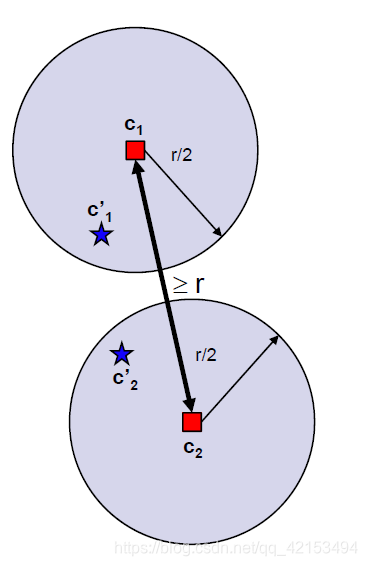
每个圆需要一个中心来服务圆心的site，导致第$k+1$个无法被服务。因此$r\le 2r^{\ast }$

2.7加权点集覆盖weighted vertex cover

建模为整数规划问题

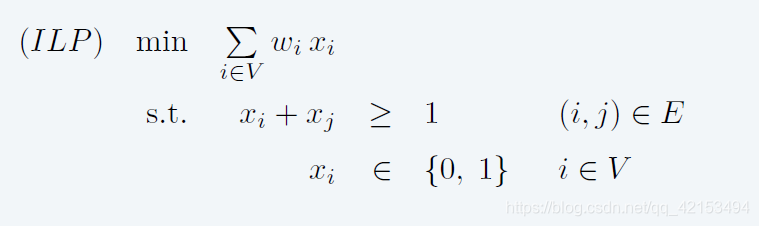
松弛为线性规划

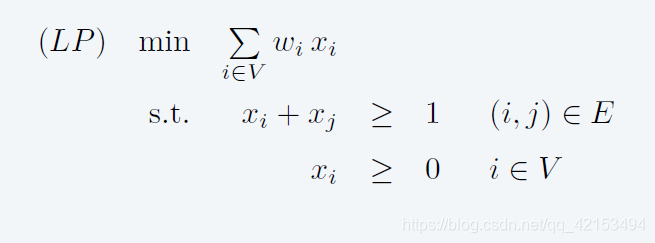
3 复杂度总结