MAML：Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks

Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks

Paper:https://arxiv.org/pdf/1703.03400.pdf
Code:https://github.com/cbfinn/maml
Tips：ICML的一篇Meta-learning相关的paper，可参考李宏毅的公开课。
（阅读笔记）

1.Main idea

• $\mathcal{A}:$We propose an algorithm for meta-learning that is model-agnostic.
• $\mathcal{B}:$给出了一个Meta-learning的解释：The goal of meta-learning is to train a model on a variety of learning tasks, such that it can solve new learning tasks using only a small number of training samples.
• $\mathcal{C}:$本文方法可以，较少的训练步骤（一般就是仅仅几步），较少的训练样本（few-shot），得到很好的效果。In our approach, the parameters of the model are explicitly trained such that a small number of gradient steps with a small amount of training data from a new task will produce good generalization performance on that task.
• $\mathcal{D}:$实验部分主要有分类，回归，强化学习。

2.Intro

• $\mathcal{A}:$又要学得快，又要学得有泛化性，那么meta-learning就是很重要的一个方法。
• $\mathcal{B}:$The key idea underlying our method is to train the model’s initial parameters such that the model has maximal performance on a new task after the parameters have been updated through one or more gradient steps computed with a small amount of data from that new task.
• $\mathcal{C}:$从特征学习的角度：can be viewed from a feature learning standpoint as building an internal representation that is broadly suitable for many tasks.
• $\mathcal{D}:$From a dynamical systems standpoint, our learning process can be viewed as maximizing the sensitivity of the loss functions of new tasks with respect to the parameters.

3.Notation

每个模型就是找到$f_{\theta }$来使输入$x_t$映射到输出$a_t$；每个任务${\mathcal{T}}_i$有如下定义： T i : { H ; q i ; L T i } \mathcal{T_i}:\{H; q_i; \mathcal{L_{\mathcal{T_i}}}\} Ti​:{H;qi​;LTi​​}

• $H$可以理解为任务的长度，对于独立同分布（i.i.d.）的分类任务来说，做一次决策即可($H=1$)；而对于一些下棋游戏等强化学习，需要有很多次的决策，则$H$值会增加。
• $q_i$表示分布。
  $Case(H=1)$:$q(x_1)$表示初始样本的分布；
  $Case(H>1)$:$q(x_{t+1}|x_t,a_t)$，每一次的决策都是上一次决策下的一个条件分布，其中第$t$次的输出即是$a_t$。
• ${\mathcal{L}}_{{\mathcal{T}}_i}$表示损失函数，就是输入$x_t$与输出$a_t$的差距，一般均方差，交叉熵损失函数。同样的，若仅仅是分类任务，仅只有$x_1$与$a_1$。

4.Details

• 有一个有很多不同任务的分布$p(\mathcal{T})$，如Omniglot就可以自由选择得到自己想要的$N-ways;K-shot$的任务，而目标是让MAML模型尽可能的适应于这个多样的任务。新的任务${\mathcal{T}}_i$通过简单的几个step，甚至是一个step，就能解决问题。
• 如果整体训练的话，可能是整体的好，可能并不会单独的某个任务好。For example, a neural network might learn internal features that are broadly applicable to all tasks in $p(\mathcal{T})$, rather than a single individual task.
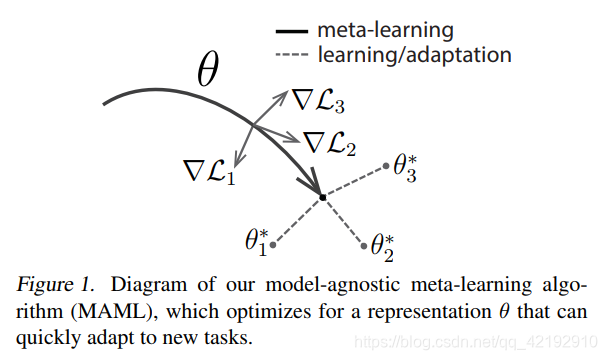
  如：mnist分成两个任务：识别1-5和识别6-10。如果整体一起训练1-10，那么模型虽然能够分别处理1-5和6-10这两个任务，不过有可能每个数字的分类不一定是其当前任务的梯度降低最优的情况。
• 如下图所示，梯度的方向。其中$\theta$是模型已经训练好了的参数，而当我们再次遇到新的Task任务${\mathcal{T}}_i$时候（图示是${\mathcal{T}}_{1，2，3}$），那么我们只需要进行梯度下降算法步骤，算出损失函数的梯度方向$▽{\mathcal{L}}_i$，那我们参数$\theta$更新的方向也为其梯度的方向，最后得到${\theta }_{1,2,3}^{\ast }$。若是对新任务仅更新参数一次即有如下式：
  $${\theta }_i^{\ast }=\theta -\alpha {▽}_{\theta }{\mathcal{L}}_{{\mathcal{T}}_i}(f_{\theta })$$
  新更新的参数${\theta }_i^{\ast }$是第$i$个新任务${\mathcal{T}}_i$在训练好的模型参数$\theta$，减去在原始$\theta$的函数$f_{\theta }$映射下的新任务的损失${\mathcal{L}}_{{\mathcal{T}}_i}$的梯度乘上$\alpha$学习率的值。（仅一次梯度更新）
  
• $\theta$这个开始训练得到的参数怎么来的呢？就是通过那一堆任务分布$p(\mathcal{T})$中抽样再训练得到的。注意到更新参数时候并不是$f_{\theta }$而是$f_{\theta }^{\ast }$，最后优化。
  $$\begin{gathered} \underset{\theta }{\min }\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{\mathcal{L}}_{{\mathcal{T}}_i}(f_{{\theta }_i^{\ast }})=\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{\mathcal{L}}_{{\mathcal{T}}_i}(f_{\theta -\alpha {▽}_{\theta }{\mathcal{L}}_{{\mathcal{T}}_i}(f_{\theta })}) \\ \theta \leftarrow \theta -\beta {▽}_{\theta }\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{\mathcal{L}}_{{\mathcal{T}}_i}(f_{{\theta }_i^{\ast }}) \end{gathered}$$
• First-order approximation：每一次优化都是对损失函数${\mathcal{L}}_{{\mathcal{T}}_i}$进行优化，那么每一次，参数$\theta$都会得到有一个${\theta }_i^{\ast }$，这么多Task${\mathcal{T}}_i$任务的影响得到最后的$\theta$。那么可以首先改写下求和顺序：
  $${▽}_{\theta }\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{\mathcal{L}}_{{\mathcal{T}}_i}(f_{{\theta }_i^{\ast }})=\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{▽}_{\theta }{\mathcal{L}}_{{\mathcal{T}}_i}(f_{{\theta }_i^{\ast }})$$
  先拿掉每个任务Task的求和符号，单独讨论一个任务的情况，对$\theta$的每一个参数（假设数目为$j$）进行微分偏导，那么最后则有下式。${\theta }_k^{\ast }$是每一个参数最后造成对${\theta }^{\ast }$的影响。$i$是初始设置的参数，而$k$是最后模型的一次梯度下降的参数。
  $${▽}_{\theta }{\mathcal{L}}_{{\mathcal{T}}_i}=\frac{\partial \mathcal{L}({\theta }^{\ast })}{\partial {\theta }_j}\to \sum _k\frac{\partial \mathcal{L}({\theta }^{\ast })}{\partial {\theta }_k^{\ast }}\times \frac{\partial {\theta }_k^{\ast }}{\partial {\theta }_j}$$
  代入${\theta }^{\ast }$与$\theta$关系则有：
  $$\frac{\partial {\theta }_k^{\ast }}{\partial {\theta }_j}=\frac{\partial ({\theta }_k-\alpha \times \frac{\partial \mathcal{L}(\theta )}{\partial {\theta }_k})}{\partial {\theta }_j}$$
  若$k$与$j$不相等，$\frac{\partial {\theta }_k}{\partial {\theta }_j}$就没有了，仅有$-\alpha \times \frac{{\partial }^2\mathcal{L}(\theta )}{\partial {\theta }_j\partial {\theta }_k}$；若$k$与$j$相等，则是$1-\alpha \times \frac{{\partial }^2\mathcal{L}(\theta )}{\partial {\theta }_j\partial {\theta }_k}$。若为了简便不想算二阶偏导，即让第一项为0，第二项为1，即是First-order approximation。
• benchmark一般用的数据集是Omniglot和mini-ImageNet。
  更具体地：MAML与迁移学习相关的pre-training是有区别的：
  • MAML是对很多组support/query set不同的task进行训练，所以模型在每一组任务的表现都会是同等条件下训练的最好结果，但是其得到的$\varphi$并不一定是（通常是）最优的解，更需要一定的小步数特定任务的训练才能达到对该任务的优秀能力，得到其参数${\hat{\theta }}^n$。可以理解为更看重这个model的潜力怎么样。
  • Pre-training是很多种不同的数据一同收敛到最优的地方，但不一定是每个具体某一类数据最优的地方，所以其处理的参数一直都是整体的参数$\varphi$。可以理解为当前这个模型一步一步训练是怎么样，结果就怎么样。
    $$\begin{gathered} \mathcal{L}(\varphi )=\sum _{n=1}^N{L}^n({\hat{\theta }}^n) \\ \mathcal{L}(\varphi )=\sum _{n=1}^N{L}^n(\varphi ) \end{gathered}$$

参考

https://danieltakeshi.github.io/2018/04/01/maml/