CS231n-Lecture3:损失函数和优化（Loss Functions and Optimization）

线性分类（Linear classification）

从图像到标签分数的参数化映射

假设图像的训练数据集$x_i\in R^D$，每个都与一个标签$y_i$相关联。我们有N个示例（每个都是D维）和K个不同的类别。例如，在CIFAR-10中，我们有一组$N$ = 50,000张图像的训练集，每个图像的$D$ = 32 x 32 x 3 = 3072像素，$K$ = 10，因为有10种不同的类别（狗，猫，汽车等）。定义得分函数$f:R^D\mapsto R^K$，将原始图像像素映射到类分数：
$$f(x_i,W,b)=W{x}_i+b$$
上式中各参数含义：

名称	大小	意义
$x_i$	D x 1	图像所有像素展平为D x 1单列矢量
$W$	K x D	权重
$b$	K x 1	偏差矢量

线性分类器的理解

1. 类比图像为高维点
   由于图像被拉伸为高维列向量，因此我们可以将每个图像解释为该空间中的单个点（例如，CIFAR-10中的每个图像都是3072维空间中32x32x3像素中的一个点）。类似地，整个数据集是一组（标记的）点。
   我们无法可视化3072维空间，想象将所有维压缩为仅二维：

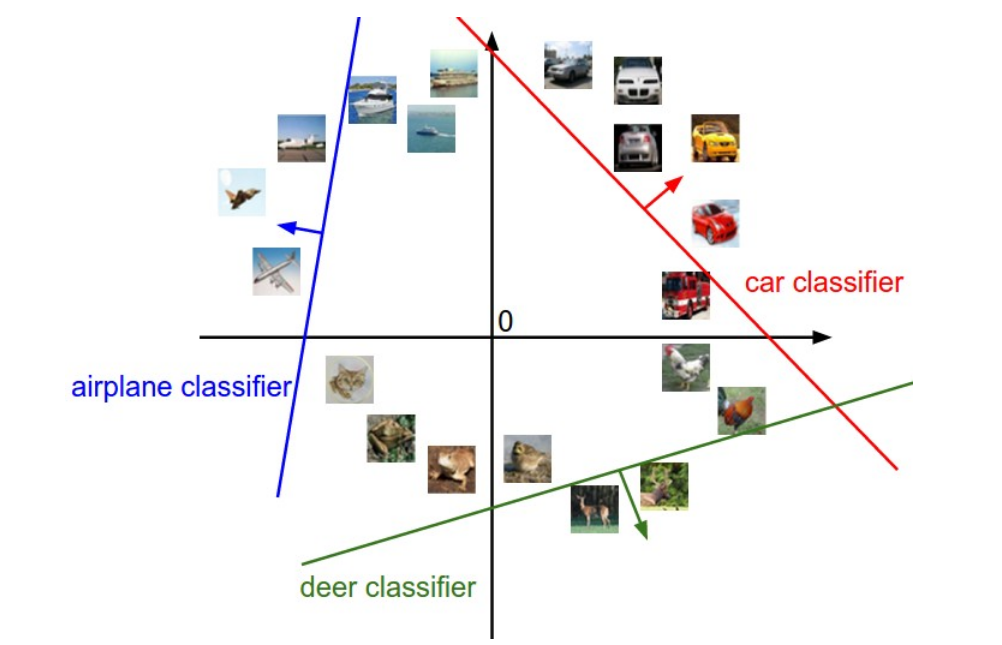
2. 将线性分类器看作模板匹配
   权重$W$的另一种解释是 $W$的每一行对应于其中一个类的模板（有时也称为原型）。然后，通过使用内积（或点积）将每个模板与图像进行比较，来获得图像的每个类别的分数。

略过一步：在学习CIFAR-10结束时，示例学习了权重。例如，ship模板按预期包含许多蓝色像素。因此，一旦该模板与海洋上的船舶图像相匹配，通过内积运算，它将获得很高的分数。

3. Bias trick
   
4. 图像数据预处理：特征缩放 / 均值归一化

损失函数

多类支持向量机（Multiclass SVM）

多类别SVM是在处理多分类问题时的对二元SVM的一种推广。在二元SVM中，只有两个类，每个样本x要么被分类成正例，要么被分类成负例；现在如果有10个类别了，就需要将二元的思想推广到多分类中。
$$L_i=\sum _{j\ne y_i}\max (0,s_j-s_{y_i}+\Delta )$$

若$\Delta =1$，则：

其中，$y_i$ 表示训练集的第i个样本的真实分类的分数，所以 $s_{y_i}$ 表示训练集的第i个样本的真实分类的分数。

上述公式的理解：

• 如果真实分类的分数比其他分数高很多，这是正确的情况，那要高出多少呢？高出一个安全的边距（这里默认为1）

• 如果真实分类的分数不能够比其他分类高出那么多，那就会得到损失，这是不好的情况。

正则化

$$L=\underset{\text{data loss}}{\underbrace{\frac{1}{N}\sum _i{L}_i}}+\underset{\text{regularization loss}}{\underbrace{\lambda R(W)}}$$
完整形式：
$$L=\frac{1}{N}\sum _i\sum _{j\ne y_i}\left[\max (0,f(x_i;W{)}_j-f(x_i;W{)}_{y_i}+\Delta )\right]+\lambda \sum _k\sum _l{W}_{k,l}^2$$

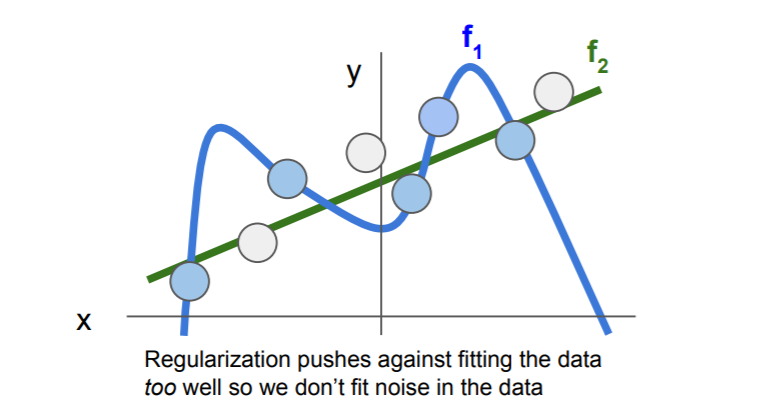
加入正则化项后，决策边界由 $f_1$变为$f_2$，惩罚项可以有效防止数据在训练集上过拟合，即趋向“更简单”的模型。

实现过程

def L_i(x, y, W):
  """
  unvectorized version. Compute the multiclass svm loss for a single example (x,y)
  - x is a column vector representing an image (e.g. 3073 x 1 in CIFAR-10)
    with an appended bias dimension in the 3073-rd position (i.e. bias trick)
  - y is an integer giving index of correct class (e.g. between 0 and 9 in CIFAR-10)
  - W is the weight matrix (e.g. 10 x 3073 in CIFAR-10)
  """
  delta = 1.0 # see notes about delta later in this section
  scores = W.dot(x) # scores becomes of size 10 x 1, the scores for each class
  correct_class_score = scores[y]
  D = W.shape[0] # number of classes, e.g. 10
  loss_i = 0.0
  for j in range(D): # iterate over all wrong classes
    if j == y:
      # skip for the true class to only loop over incorrect classes
      continue
    # accumulate loss for the i-th example
    loss_i += max(0, scores[j] - correct_class_score + delta)
  return loss_i

def L_i_vectorized(x, y, W):
  """
  A faster half-vectorized implementation. half-vectorized
  refers to the fact that for a single example the implementation contains
  no for loops, but there is still one loop over the examples (outside this function)
  """
  delta = 1.0
  scores = W.dot(x)
  # compute the margins for all classes in one vector operation
  margins = np.maximum(0, scores - scores[y] + delta)
  # on y-th position scores[y] - scores[y] canceled and gave delta. We want
  # to ignore the y-th position and only consider margin on max wrong class
  margins[y] = 0
  loss_i = np.sum(margins)
  return loss_i

def L(X, y, W):
  """
  fully-vectorized implementation :
  - X holds all the training examples as columns (e.g. 3073 x 50,000 in CIFAR-10)
  - y is array of integers specifying correct class (e.g. 50,000-D array)
  - W are weights (e.g. 10 x 3073)
  """
  # evaluate loss over all examples in X without using any for loops
  # left as exercise to reader in the assignment

Softmax分类器

SVM将输出$f(x_i,W)$作为每个类别的分数（未校准且难以解释），而Softmax分类器给出的输出更为直观（标准化的概率）。
首先给出Softmax函数
$$P(y_i\mid x_i;W)=\frac{e^{f_{y_i}}}{{\sum }_j{e}^{f_j}}$$

在Softmax中，用交叉熵损失（cross-entropy loss） 代替合页损失（hinge loss）：
$$L_i=-\log \left(\frac{e^{f_{y_i}}}{{\sum }_j{e}^{f_j}}\right)\text{or equivalently}{L}_i=-f_{y_i}+\log \sum _j{e}^{f_j}$$

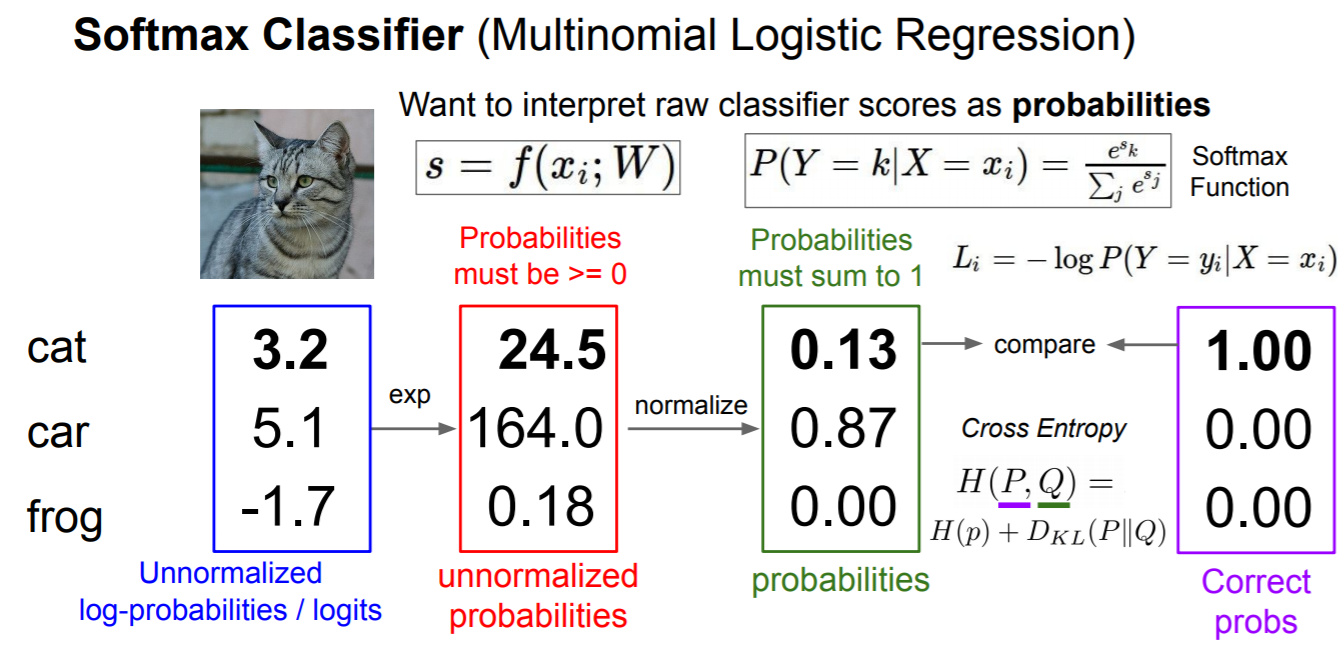
SVM与Softmax

在这两种情况下，我们都计算相同的分数矢量f。区别在于对f分数的解释：

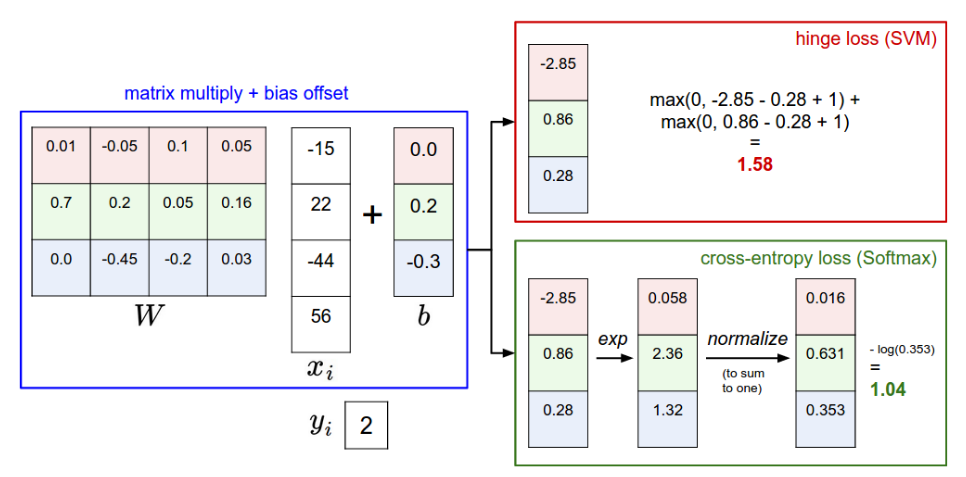
• SVM将这些解释为类别得分，其损失函数鼓励正确的类别（蓝色的class 2）的得分比其他班级的得分高一点。
• Softmax分类器将分数解释为每个类别的（未归一化）对数概率，然后鼓励正确类别的（归一化）对数概率较高（等效地，错误类别较低）。

SVM和Softmax通常是可比较的：

• SVM不在乎单个分数的细节：如果它们分别是[10，-100，-100]或[10，9，9]，则由于满足1的裕度，因此SVM不会造成任何损失是零。一旦满足边距，SVM就会很高兴，并且不会对超出这一限制的确切分数进行微管理。
• 但是，对于Softmax分类器，后者会为得分[10，9，9]累积比[10，-100，-100]高得多的损失。换句话说，Softmax分类器对它产生的分数永远不会完全满意：正确的分类总是有较高的概率，而错误的分类总是有较低的概率，损失总是会更好。

优化（Optimization）

计算梯度

有两种计算梯度的方法：一种缓慢，近似但简单的方法（数值梯度），以及一种快速，精确但更容易出错的方法，需要进行演算（解析梯度）。

"""
function : f(x,y,z) = (x+y)z
"""

1. 用有限差分数值计算梯度（数值梯度）

# second method  数值法
# increment by epi
def grad2(x,y,z,epi): 
    # dx
    fx1 = (x+epi+y)*z
    fx2 = (x-epi+y)*z
    dx = (fx1-fx2)/(2*epi)
    # dy
    fy1 = (x+y+epi)*z
    fy2 = (x+y-epi)*z
    dy = (fy1-fy2)/(2*epi)
    # dz
    fz1 = (x+y)*(z+epi)
    fz2 = (x+y)*(z-epi)
    dz = (fz1-fz2)/(2*epi)
    return (dx,dy,dz)

2. 用微积分分析计算梯度（解析梯度）

# first method   解析法
def grad1(x,y,z):
    dx = z
    dy = z
    dz = (x+y)
    return (dx,dy,dz)

梯度下降

重复评估梯度然后执行参数更新的过程称为梯度下降：

# Vanilla Gradient Descent

while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # perform parameter update

小批量梯度下降（Mini-batch gradient descent / MBGD），是对批量梯度下降（BGD）以及随机梯度下降（SGD）的一个折中办法。其具体思路是：每次迭代使用 $batc{h}_{size}$个样本来对参数进行更新。
这里我们假设 $batc{h}_{size}$=10 ，样本数 m=1000 。

  伪代码形式为：
  repeat{
    for i=1,11,21,31,…,991{
      ${\theta }_j:={\theta }_j-\alpha \frac{1}{10}{\sum }_{k=i}^{(i+9)}(h_{\theta }(x^{(k)})-y^{(k)})x_j^{(k)}$
      (for j =0,1)
     }
   }

例如，在当前最先进的ConvNets中，一个典型的批次包含120万个整个训练集中的256个示例。然后使用该批处理执行参数更新：

# Vanilla Minibatch Gradient Descent

while True:
  data_batch = sample_training_data(data, 256) # sample 256 examples
  weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
  weights += - step_size * weights_grad # perform parameter update

reference

[1]计算梯度的三种方法： 数值法，解析法，反向传播法
[2]批量梯度下降(BGD)、随机梯度下降(SGD)以及小批量梯度下降(MBGD)的理解