【Games101】Lecture04 变换-续 笔记

视频&图片来源：【B站】GAMES101-现代计算机图形学入门-闫令琪

1. 三维变换

1.1 仿射变换

齐次坐标下的仿射变换：$\left(\begin{array}{c}{x}^{{}^{\prime }}\\ y^{{}^{\prime }}\\ z^{{}^{\prime }}\\ 1\end{array}\right)=\left(\begin{array}{cccc}a& b& c& t_x\\ d& e& f& t_y\\ g& h& i& t_z\\ 0& 0& 0& 1\end{array}\right)\cdot \left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)$
先线性变换，再平移：

• 缩放矩阵：$S(s_x,s_y,s_z)=\left(\begin{array}{cccc}{s}_x& 0& 0& 0\\ 0& s_y& 0& 0\\ 0& 0& s_z& 0\\ 0& 0& 0& 1\end{array}\right)$
• 平移矩阵：$T(t_x,t_y,t_z)=\left(\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right)$
• 绕轴旋转：
  沿X轴：$R_x(\alpha )=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \alpha & -\sin \alpha & 0\\ 0& \sin \alpha & \cos \alpha & 0\\ 0& 0& 0& 1\end{array}\right)$
  沿Y轴：$R_y(\alpha )=\left(\begin{array}{cccc}\cos \alpha & 0& \sin \alpha & 0\\ 0& 1& 0& 0\\ -\sin \alpha & 0& \cos \alpha & 0\\ 0& 0& 0& 1\end{array}\right)$ 循环对称性
  沿Z轴：$R_z(\alpha )=\left(\begin{array}{cccc}\cos \alpha & -\sin \alpha & 0& 0\\ \sin \alpha & \cos \alpha & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$

1.2 任意的旋转

3D下任意的旋转，都可以分解成绕X轴、绕Y轴、绕Z轴的旋转。
即：$R_{xyz}(\alpha ,\beta ,\gamma )=R_x(\alpha )R_y(\beta )R_z(\gamma )$，其中$\alpha ，\beta ，\gamma$称为欧拉角

• 罗德里格斯旋转公式：绕轴n旋转$\alpha$度
  $R(n,\alpha )=\cos (\alpha )I+(1-\cos (\alpha ))n{n}^T+\sin (\alpha )\left(\begin{array}{ccc}0& -n_z& n_y\\ n_z& 0& -n_x\\ -n_y& n_x& 0\end{array}\right)$
  这里的轴n默认过原点，否则会出现方向上的问题

• 推广：如果绕任意点/任意轴旋转，基本思路是把这个点平移到原点/使轴过原点，旋转完再平移回之前的位置

2. 观测变换 Viewing transformation

一个引入例子：拍照

1. 找一堆人来拍👉模型变换（Model）
2. 找一个拍照角度，改变相机位置👉视图变换（View）
3. 拍照！👉投影变换（Projection）

2.1 视图（View）/ 相机变换

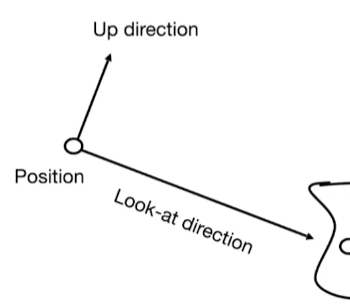
如何确定相机的位置：

• 放置相机的位置：$\overrightarrow{e}$
• 视线方向，朝哪看（Look-at/gaze direction）：$\hat{g}$
• 朝向上的方向：$\hat{t}$

一个特性：当相机和物体之间保持相对静止，即相机和被拍摄物之间的位置关系不发生改变，则移动相机或被拍摄物，拍摄结果也不会发生改变。


基于该特性，一般默认：相机永远固定在原点位置上，看向$-Z$轴方向，以$Y$轴为向上方向。


从上图到下图的基本思想：

• $\overrightarrow{e}$作平移，移动到原点
• $\hat{g}$移动到$-Z$方向上
• $\hat{t}$旋转到$Y$方向上
• $\hat{g}\times \hat{t}$得到的向量旋转到$X$方向上

用矩阵形式表示：$M_{view}=R_{view}{T}_{view}$，$T_{view}=\left[\begin{array}{cccc}1& 0& 0& -x_e\\ 0& 1& 0& -y_e\\ 0& 0& 1& -z_e\\ 0& 0& 0& 1\end{array}\right]$
关于$R_{view}$，直接求不好求，可以用$R_{view}^{-1}$（逆变换，相当于世界坐标系变为相机的坐标系）求：
$R_{view}^{-1}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& x_t& x_{-g}& 0\\ y_{\hat{g}\times \hat{t}}& y_t& y_{-g}& 0\\ z_{\hat{g}\times \hat{t}}& z_t& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]\Rightarrow R_{view}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& y_{\hat{g}\times \hat{t}}& z_{\hat{g}\times \hat{t}}& 0\\ x_t& y_t& z_t& 0\\ x_{-g}& y_{-g}& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]$

2.2 投影变换

2.2.1 正交投影

一个简单的正交投影做法：

• 相机放在原点，看向$-Z$方向，向上为$Y$方向（通用的摆放方式）
• 扔掉$Z$的坐标，只剩下$X和Y$得到的结果直接是平面上的图像
• 不管原始的$x和y$有多大，经过平移和缩放，使图像落在$[-1,1{]}^2$的范围内（约定俗成的做法）
  
  图形学上的变化方法：
• 定义空间中的立方体，左右在$X$轴作用，下上在$Y$轴上作用，远近在$Z$轴上作用（Z值近大远小）
• 把该立方体映射到标准立方体$[-1,1{]}^3$上（先平移再缩放）
  矩阵形式：
  $M_{ortho}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right]$
  注：$n-near;f-far;t-top;b-bottom;l-left;r-right$
  再注：完成投影变换后，无论原始物体的长宽比如何，经过缩放后长宽比会发生改变，精度也可能有问题，后续还有其他处理。

2.2.2 透视投影

带来的一个结果：平行线不再平行（指透视延伸）

齐次坐标的性质：$(x,y,z,1)；(kx,ky,kz,k)，k\ne 0；(xz,yz,z^2,z)，z\ne 0$，表示的都是同一个点$(x,y,z)$。

规定：

• 近平面永远不变（四个点固定，平面上的任何一个点同理）
• 远平面$Z$值/轴 不变（平面向内收缩）
• 远平面中心点不变

思考：远平面向内压缩时，平面上的点的深度值如何变大？（点往近了跑还是往远了跑？）

• 盲猜变远…压缩会把多出来的点压到靠后的位置…