Games101学习笔记-Lecture3~4

一、2D线性变化

我们将如下图所示的简单矩阵乘法定义为对向量( x , y ) T 的线性变换。

1.缩放(scaling)

缩放变换是一种沿着坐标轴作用的变换，即除了( 0 , 0 ) T保持不变之外，所有的点变为( s x , s y )T，缩放矩阵：

2.反射(reflection)

反射矩阵

3.错切(shear)

shear变换直观理解就是把物体一边固定，然后拉另外一边，错切矩阵：

 以下分别对应拉伸x轴和拉伸y轴,s为斜率的倒数（由y = 1/sx得来，即x的偏移量为sy）。

4.旋转(rotation)

①旋转矩阵：

②推导方法：

记向量长度为r，则得出

向量b得坐标：

则得出

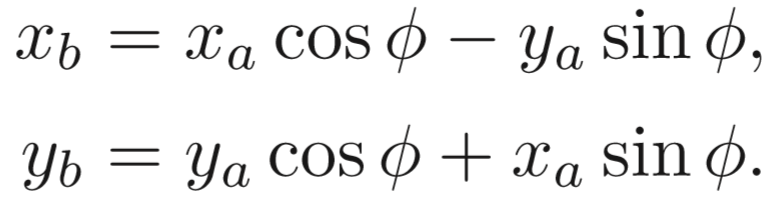
最后得旋转矩阵为（注意该式为逆时针旋转，且原点为旋转中心）

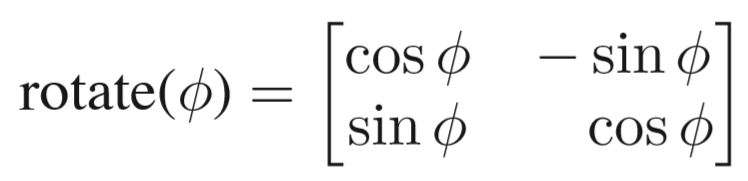
二、齐次坐标

用于更好得将位移与旋转、缩放结合在一起。（把平移操作变成线性关系）

注:向量具有平移不变性，不管向量如何平移都不应该发生变换。

•  向量+向量，三角形法则，得到另外一条向量（首位相接）

• 点-点，得到ponit右直向point左的向量

• 点+向量，点沿着向量得方向移动，得到新的点

• 点+点，会得到两个点的中点（两点相加w会变成2，要转化成point则要处于2）

1.仿射变换

2.逆变换

逆变换相当于再乘以一个原先变换的逆矩阵；

 

 注:有正交性的矩阵的逆矩阵为其转置矩阵。

三、合成变换

从右到左进行应用，可以先计算所有变换矩阵的乘积，再与变换的数据相乘

围绕任意一个点进行旋转的操作

四、3D变化

三维空间引入齐次坐标

 三维空间进行仿射变换

1.缩放

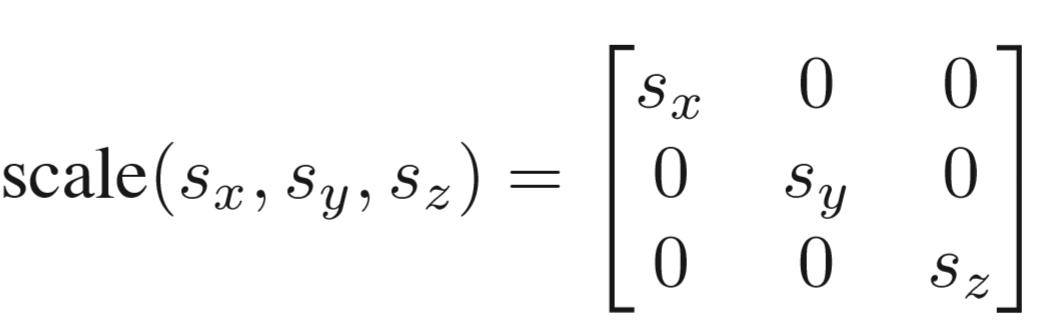
2.剪切

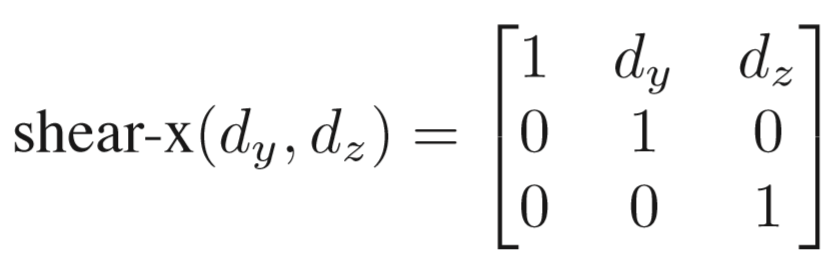
3.旋转

三维维旋转有3个矩阵，分别对应绕x轴，y轴，z轴旋转，同时有很关键的一点要注意！我们所采用的是右手系，因此旋转是有定向(orientation)正如在二维，是x轴向y轴旋转，对应到三维便是绕z轴旋转(x轴转向y轴)，不难推出绕x轴旋转(y转向z)，绕y轴旋转(z转向x)。

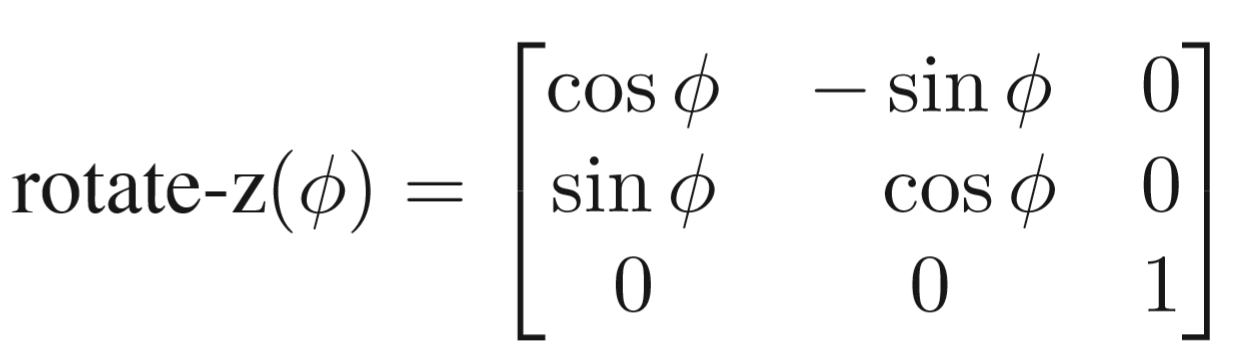
绕z轴，所有z不变，x转向y。

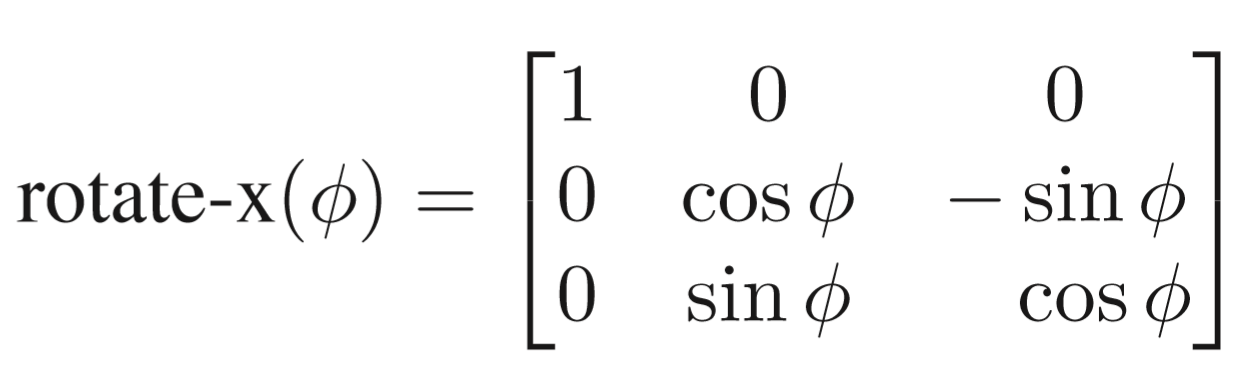
绕x轴，所有x不变，y转向z。

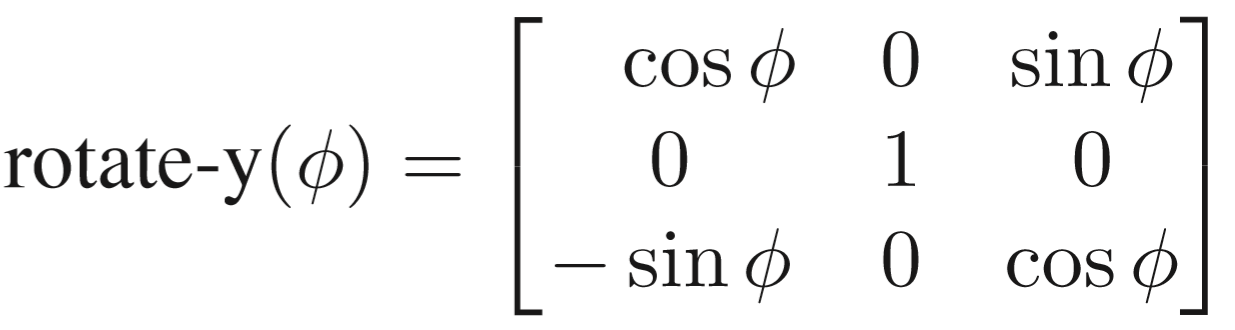
绕y轴，y不变，z转向x。因为计算顺序为XZ，而XZ在右手定律中为顺时针，顺时针旋转了了Φ，相当于逆时针旋转了-Φ，等于说要对顺时针旋转Φ的旋转矩阵求转置矩阵。

4.绕任意轴旋转

任意的一个旋转都可以被分解成由绕x，y，z轴的三个旋转组成的一个旋转。

这三个角被称为欧拉角，常用于飞行模拟器：滚转、俯仰、偏航

①罗德里格斯旋转公式：

其中I为单位矩阵，为旋转轴基向量的模长，N为叉积的矩阵表示

②推导过程：

罗德里格斯公式一般可以表示为：

其中代表新得到的向量，代表原向量，代表所旋转的向量分解得到旋转轴的平行部分（v到n轴的投影）。

(1)向量在与n轴垂直的平面内旋转

要将转化为已知向量，可以通过合成的方法，利用叉积解决。

垂直n轴的平面如图：

由于以n为基向量，可知的模长与和原向量一致，所以可以利用向量加法合成：

(2)考虑一般情况下的旋转

对进行分解，可以分解为和，如图：

根据上图的分解，我们可知，同时

根据第一步求出的公式，可得到：

即。

因为代表在n轴上的投影，所以。

又因为叉积满足结合律，所以可知，

由于n轴和共线，所以，即。

将以上结论代入公式，可得：

令，则得到

N为由n得到的反对称矩阵，推导过程为如下：

5.平移

五、观察变化

1.视图变换(摆放相机)

(1) 模型变换(modeling tranformation)：这一步的目的是将虚拟世界中或者更具体点，游戏场景中的物体调整至他们应该在的位置，利用基础的变换矩阵将世界当中的物体调整至我们想要的地方(旋转，平移，缩放)

(2) 摄像机变换(camera tranformation)：在游戏中我们真正在乎的是摄像机(或者说眼睛)所看到的东西，也就是需要得到物体与摄像机的相对位置

①变换过程

如何将camera的坐标系与原世界坐标系重合呢？我们先定义3个东西：

相机或眼睛位置 (eye postion) e
观察方向 (gaze postion) g
视点正上方向 (view-up vector ) t

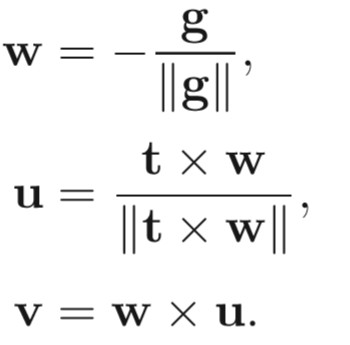
其中u，v，w分别对于标准坐标系下的x，y，z，示意图如下：

然后把摄像机平移到原点并通过旋转将摄像机坐标与世界坐标重合。

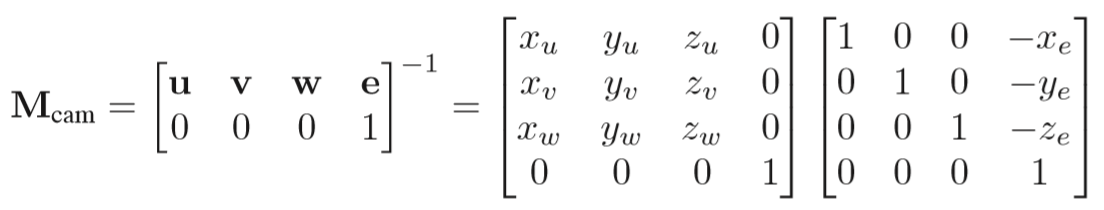
②Games101：

(3) 投影变换(projection tranformation)：根据摄像机变换得到了所有可视范围内的物体对于摄像机的相对位置坐标(x,y,z)之后，便是根据是平行投影还是透视投影，将三维空间投影至标准二维平面([-1,1]^2)之上 （tips：这里的z并没有丢掉，为了之后的遮挡关系检测）

①正交投影

数学的矩阵表示
立方体t代表top，b是bottom，lr是左和右，nf分别是near和far

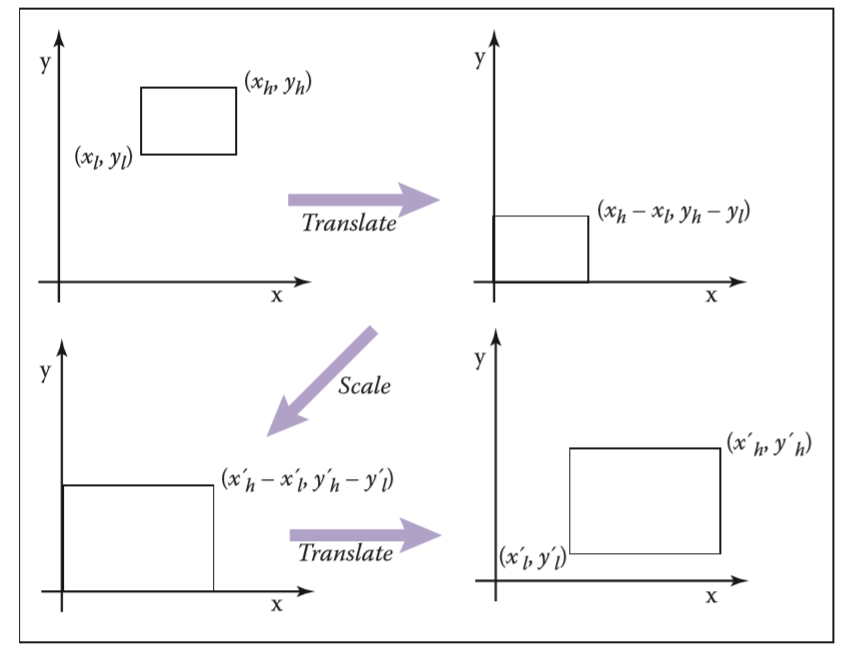
Ⅰ 将原空间范围的左下角移至原点
Ⅱ 放大给定倍数
Ⅲ 将缩放后的空间范围移至新空间范围

再带入数据，缩放到一个边长为2的正方体:，则得到的正交变换矩阵如下：

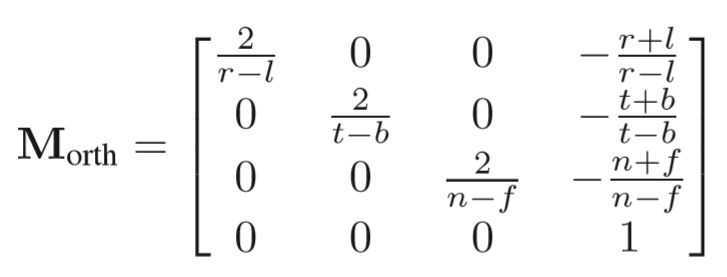
②透视投影

将(x,y,z)一点投影到投影屏幕之后，坐标变为(x’,y’,z’)

其中，z=-n代表投影平面，利用齐次坐标的性质，可以得到如下矩阵变换：

如果形象化的描述一下的话，就是利用这个变换矩阵将整个空间压缩了一下，使其对应了真正透视投影的坐标，最后不要忘了要利用正交转换到[ − 1 , 1 ] 3的空间之内，根据齐次坐标可得：

运用透视投影的一个性质，可视空间前后变换之后z坐标不变则可设第三行为(0,0,A,B)，

并带入远近平面任意两点就可以列出等式：

这是由于 y’ = ny/z不好做线性变换，所以放大z倍，求解时代入了z=n，z=f

可得矩阵：

最后将被压缩过的空间重新正交投影为标准小立方体，故定义透视投影变换为：

计算结果如下：

(4) 视口变换(viewport transformation)：将处于标准平面映射到屏幕分辨率范围之内，即[-1,1]2→ rightarrow→[0,width]*[0,height], 其中width和height指屏幕分辨率大小