SD3的采样下篇——Rectified Flow

李歘歘

已于 2024-12-11 00:03:16 修改

阅读量1.9k

点赞数 34

分类专栏：人工智能 # AIGC # SD 文章标签： SD 人工智能深度学习 transformer DiT stable diffusion RF

于 2024-11-27 16:25:54 首次发布

本文链接：https://blog.csdn.net/qq_42410605/article/details/144068472

版权

人工智能同时被 3 个专栏收录

56 篇文章

订阅专栏

AIGC

25 篇文章

订阅专栏

17 篇文章

订阅专栏

在这里插入图片描述

🌺系列文章推荐🌺
扩散模型系列文章正在持续的更新，更新节奏如下，先更新SD模型讲解，再更新相关的微调方法文章，敬请期待！！！（本文及其之前的文章均已更新）
扩散模型相关知识点参考：小白也能读懂的AIGC扩散（Diffusion）模型系列讲解

文章目录

RF的扩散

论文

SD3论文：Scaling Rectified Flow Transformers for High-Resolution Image Synthesis
FLUX.1论文：未公开
Flow Matching论文：FLOW MATCHING FOR GENERATIVE MODELING
Rectified Flow论文：Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow 和 Rectified Flow: A Marginal Preserving Approach to Optimal Transport

前系列扩散回顾（DDPM）

关于之前SD系列扩散模型的扩散核心采样使用DDPM、DDIM等。扩散过程本质上是多次对原始图像前向扩散（加噪），之后在训练过程中学习如何准确的预测加入的真实噪声。进而在推理过程中，对初始的随机噪声进行预测噪声，进而反向扩散（去噪），得到想要图像的过程。可以看作是一种迂回方式。扩散过程如下：
在这里插入图片描述
借用某乎上大佬的图(来源)来描述整个扩散过程如下：
前向传播：这里的每一个点（注意，是点，不是整个框），其实就对应于图像空间的一张图（上图中的小猫），蓝色箭头就是在不断加噪的过程，每次随机加入一定强度的噪声。一个前向传播如下：
在这里插入图片描述

反向传播：依据训练过程中学到的预测噪声能力，把预测出来的噪声去除，逐步恢复图像。蓝色箭头就是在不预测并去除噪声的过程。2个反向传播过程如下：

不是严格的从某个点映射到某个点了。而是从高斯噪声空间随机采样一个点，然后依次往回映射。假设模型已经训练好了，这时候其实靠的就是模型的泛化能力了。假如在高斯噪声空间，你采样了个红点附近的噪声，那么模型只能保证你映射回图像的时候也在红点附近。

在这里插入图片描述
详细的扩散过程可以参考：
Diffusion Model
Stable Diffusion的加噪和去噪详解

写在开头

SD3是基于 RF（Rectified Flow）做的改进的采样方法，而RF（Rectified Flow）是在Flow Matching（FM）的基础上改进的，我们是按照逆序进行讲解，即先讲FM，再讲RF和SD3在其基础上做的优化。

RF（Rectified Flow）是在Flow Matching（FM）的基础上改进的，不了解Flow Matching（FM）的请先阅读SD3的采样上篇——Flow Matching。RF和SD3在其基础上做的优化放在后篇。下面正式开始介绍RF和SD3在RF基础上做的优化！！！

Rectified Flow（RF）详细介绍

Rectified Flow (RF) 是一种基于 Flow Matching (FM) 的改进技术，通过简化流动路径和优化采样过程，显著提升了生成模型的效率和稳定性。Rectified Flow 的核心是利用 直线路径或者分段线性变换 和 梯度修正，为复杂的高分辨率数据生成任务提供高效、稳定的解法。

Rectified Flow (RF) 是对 Flow Matching 的简化和优化，通过假设起始分布到目标分布的流动路径为 直线路径或分段线性路径（当直线路径无法很好地描述复杂分布之间的流动时，RF 支持将路径划分为多个时间段），并引入梯度修正项 $r (x, t)$ ，显著降低了计算复杂度并提升数值稳定性。在 RF 中，数据沿着直线路径流动，同时修正项对路径的偏差进行调整，使得生成结果更接近目标分布。RF 的这一改进减少了采样步数需求，并且在混合精度训练中表现更稳定。与 FM 相比，RF 更适用于高分辨率生成任务和复杂模态的联合建模，如 SD 3 和 FLUX 系列模型，均采用 RF 来优化其扩散过程。

1. 背景与核心思想

Flow Matching (FM):
FM 是一种通过定义概率流动（probability flow）来训练生成模型的方法。目标是构造一个向量场，使得样本从初始分布到目标分布的变换遵循光滑的连续路径。但在实际应用中，存在以下问题：
1. 路径复杂性：学习到的流动路径通常是非线性的连续曲线，导致建模难和增加计算开销。
2. 采样效率低：生成过程中需要高频采样，计算代价较高。
3. 数值不稳定性：流动路径复杂时，可能导致数值精度问题，特别是在高分辨率数据中。
Rectified Flow（RF）的改进:
FM 的直接应用在处理高分辨率复杂数据时可能会遇到路径优化困难、采样效率低等问题。RF 针对这些问题进行了改进，通过分段线性变换和梯度修正来简化路径并增强稳定性。
- 简化流动路径：假设起始分布和目标分布之间的流动路径为 直线路径 或 分段线性路径，简化了学习过程。
- 引入梯度修正：在简化路径的基础上，通过梯度流修正优化生成质量和准确性。
- 提升采样效率：结合分段线性变换，减少生成所需的步数，从而提升采样速度。

总结：

FM 的路径是曲线，由速度场控制，灵活但计算成本较高。
RF 的路径默认是直线，这是其原始定义中的核心假设，主要目的是简化流动建模过程。SD3论文中使用的就是直线，详情查看下面的直线路径相关内容。
RF的路径可以扩展到分段线性路径，在处理非常复杂的分布（如多模态分布或高维稀疏数据）时，直线路径无法很好地描述复杂分布之间的流动时，RF 支持将路径划分为多个时间段。【这里不详细展开此方法】

2. Rectified Flow 的关键组成

直线变换和分段线性变换
- RF 采用了一种分段线性或者直线直线变换的方法来优化从初始分布到目标分布的路径。
- 这通过将路径划分为多个线性段或者直线变换，每段都经过特定优化，以确保过渡的平滑性和一致性。
- 优势：
  - 降低复杂性：分段线性变换/直线变换比传统的非线性路径计算更简单。
  - 提高效率：分段变换/直线变换允许快速近似复杂的流动路径。
梯度修正
- 传统 FM 方法中，直接拟合流动向量场可能会因目标分布的高维复杂性导致误差累积。
- RF 引入梯度修正（Gradient Rectification），即在流动过程中动态调整路径，使其更接近目标分布的梯度信息。
- 梯度修正通过优化目标分布的近似梯度，引导生成路径避免偏离。

路径修正

这里的路径是正向过程中的定义，这类似于扩散模型中的正向扩散（加噪）过程。下面介绍的是直线路径

RF 的核心假设确实是从起始分布（通常是数据分布 $p_0$ ）到目标分布（通常是标准正态分布 $p_1$ ）的流动路径为 直线路径。
这条路径的表达为：
$z_t = (1-t)x_0 + t\epsilon,$
其中 $\in [0, 1]$ 是时间步， $x_0 \sim p_0$ ， $\epsilon \sim \mathcal{N}(0, I)$ 。

在SD3论文中使用的就是直线路径，还有一些额外的解释如下：
公式中 $x_0$ 是数据分布的样本， $\epsilon$ 是标准正态噪声， $\in [0, 1]$ 是时间步。

使用的损失是 $\mathcal{L}_{CFM}$ ，其权重为 $w_t^{RF} = \frac{t}{1-t}$ 。
网络的输出直接拟合向量场 $\mathbf{v}_\Theta$ 。
矫正流RF是一种通过直线插值的方式来链接数据分布和高斯分布的方法。
权重 $w_t^{RF}$ 表示时间步 $t$ 的加权程度，权重随着 $t$ 的增大而线性增加，使得模型更关注晚期的转换。

梯度修正

上述直线路径的梯度是对路径公式对时间 $t$ 求导，得到路径的基本梯度：
$\frac{\partial z_t}{\partial t} = \epsilon - x_0.$
在直线路径上，引入梯度修正项 $r (x, t)$ ，用于调整数据点在流动过程中的偏差：
$\frac{\partial z_t}{\partial t} = (\epsilon - x_0) + r(z_t, t)$
- $(\epsilon - x_0)$ ：是直线路径的基本梯度；
- $r(z_t, t)$ ：梯度修正项，由模型动态学习，用于调整路径流动，使其更符合概率流动的真实梯度。
- 修正后的流动路径能够更精确地拟合从 $p_0(x)$ 到 $p_1(x)$ 的真实概率流。

$\frac{\partial z_t}{\partial t}$ 在 Flow Matching 和 Continuous Flow Matching 中被隐式包含在目标向量场 $u_t(z \mid \epsilon)$ 中。

修正项目标：
修正项 $r(z_t, t)$ 的目标是学习真实概率流的梯度：
$r(z_t, t) \approx \nabla_{z_t} \log p(z_t, t),$
即数据分布 $p(z_t, t)$ 在时间 $t$ 下的梯度。

3.RF的训练和推理

在计算 Flow Matching (FM) 或 Continuous Flow Matching (CFM) 的过程中，如果将 直线路径修正 和 梯度修正 的思想合并进去，就可以得到 Rectified Flow (RF) 的完整流程。这两个修正过程本质上是 RF 的核心特征，它们增强了模型对数据分布与目标分布之间流动过程的描述能力。FM的训练和生成流程参考：Rectified Flow采样方法的训练与生成过程

4. Rectified Flow 的优点

(1) 路径简化

假设分布之间的流动路径为直线路径，大幅简化了流场的建模。
消除了非线性路径带来的计算复杂性。

(2) 生成质量提升

梯度修正项 (r(x, t)) 的引入，使得模型能够更准确地拟合真实概率流。
即使路径被简化为线性，修正项仍能捕捉细粒度特征，保证生成质量。

(3) 高效采样

分段线性路径减少了生成过程的步数。
修正项进一步优化了生成过程，使得模型能够快速生成高分辨率样本。

(4) 数值稳定性

通过简化路径和分段优化，Rectified Flow 避免了数值不稳定性，特别是在混合精度训练（FP16）中效果显著。

写在结尾

在SD3的论文中，考虑了FM的不同变体，不仅仅描述了RF采样方法，还描述了EDM、Cosine、(LDM-)Linear ，如下图：
在这里插入图片描述
同时，还针对RF型号定制了SNR采样器（3.1. Tailored SNR Samplers for RF models）。
这里不做过多的描述了，感兴趣的同学可以在原文中自行查看。

RF的扩散

这里借用某乎上大佬的图(来源)来描述整个扩散过程如下：

1. 前向扩散

如下图黑色箭头：

在这里插入图片描述

样本 $z_t$ 是从数据分布 $p_0$ 到噪声分布 $p_1$ 的路径 $p_t$ ，路径通常是直线，一步到位，由时间 $\in [0, 1]$ 和插值参数 $a_t, b_t$ 控制的。这个过程是基于公式：
$z_t = (1-t)x_0 + t\epsilon,$
其中 $\in [0, 1]$ 是时间步， $x_0 \sim p_0$ ，即从目标数据分布中采样的样本。， $\epsilon \sim \mathcal{N}(0, I)$ 。

黑色箭头表示的直线路径确实符合 $z_t$ 的概率流从 $p_0$ 到 $p_1$ 的行为。
“一步到位” 在这里是指，整个前向扩散路径是连续的，不需要离散的逐步加噪（比如 DDPM 中的逐步噪声添加）。

补充说明
前向扩散是一个固定的物理过程，其核心目标是生成一个平滑的理论路径 $p_t(z_t)$ ，这个路径并不直接参与优化，而是为训练模型的向量场 $v_\Theta$ 提供参考。

2. 反向扩散

如下图黑色箭头：
在这里插入图片描述

学到的向量场 $v_\Theta(z, t)$ 控制从噪声分布 $p_1$ 到数据分布 $p_0$ 的概率路径。
通过 ODE 反向积分，可以沿着学到的路径一步到位恢复图像。

补充：

反向过程并非真的“一步完成”，而是利用连续的微分方程描述路径，并通过 ODE 解算器逐步逼近生成结果。
ODE 解算器（如 Runge-Kutta 方法）会在离散的时间步中计算积分，但相比 DDPM 的数百步去噪，FM 的反向过程所需的离散步数远少得多。

反向扩散公式为：
$\frac{\partial z_t}{\partial t} = \epsilon - x_0.$
在直线路径上，引入梯度修正项 $r (x, t)$ ，用于调整数据点在流动过程中的偏差：
$\frac{\partial z_t}{\partial t} = (\epsilon - x_0) + r(z_t, t)$

$(\epsilon - x_0)$ ：是直线路径的基本梯度；
$r(z_t, t)$ ：梯度修正项，由模型动态学习，用于调整路径流动，使其更符合概率流动的真实梯度。

补充

在此文中，博主提到：

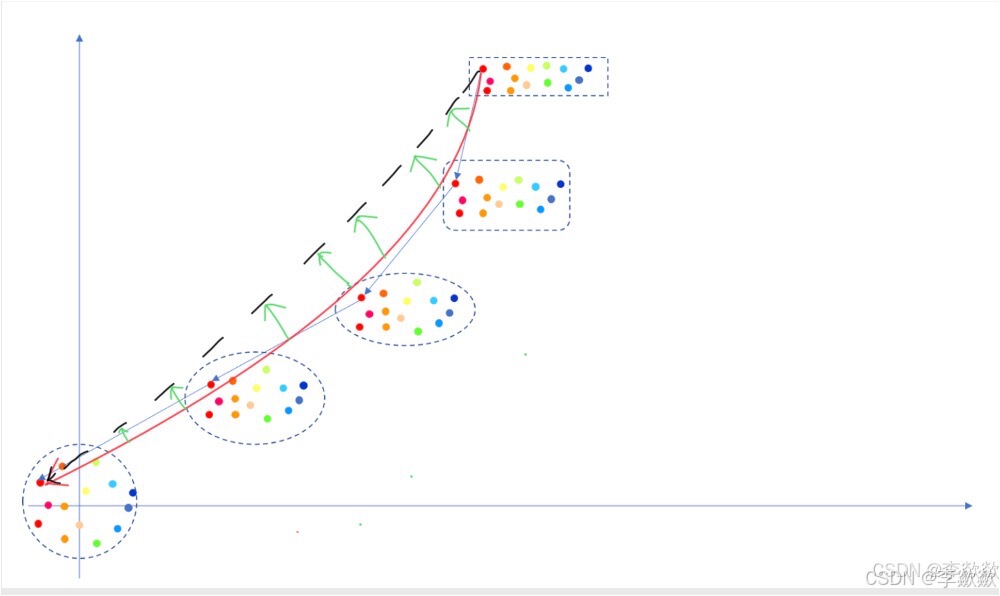
RF方法和蒸馏对比着看更容易理解。Rectified flow就是把之前画的那条蓝色箭头线，一点一点的拉着它让他跟黑色线去靠近，靠的越近不就越直了嘛，如果说蓝色箭头组成的线叫一个流，那这个方法就叫整流。如下图：

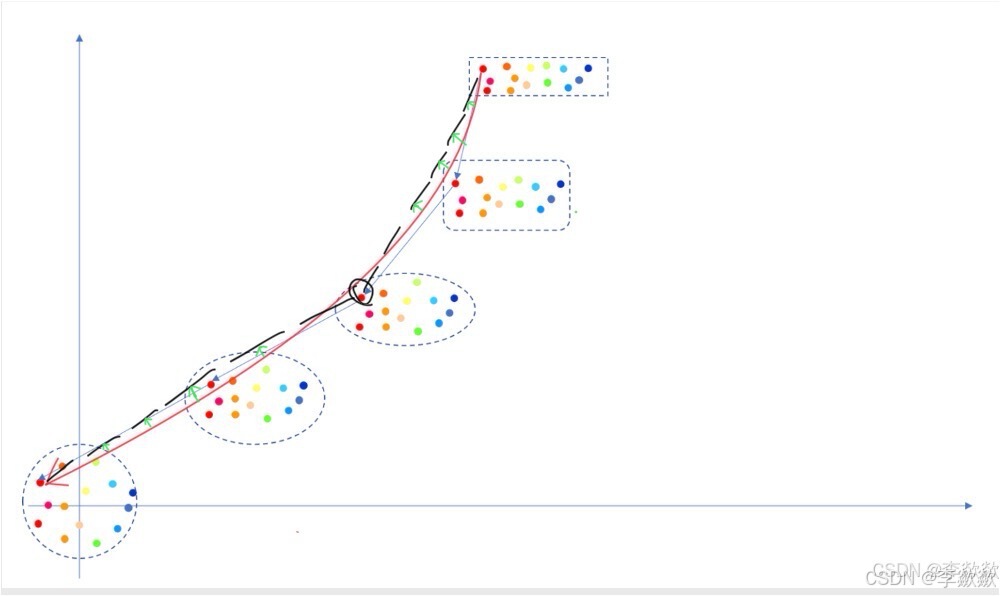
本人认为，不应该拉蓝色箭头线，蓝色箭头是传统使用DDPM的扩散模型的扩散过程，拉FM的红色箭头更合适一点（FM的箭头表示参考SD3的采样上篇——Flow Matching），毕竟RF是在FM的基础上优化的。如下图：
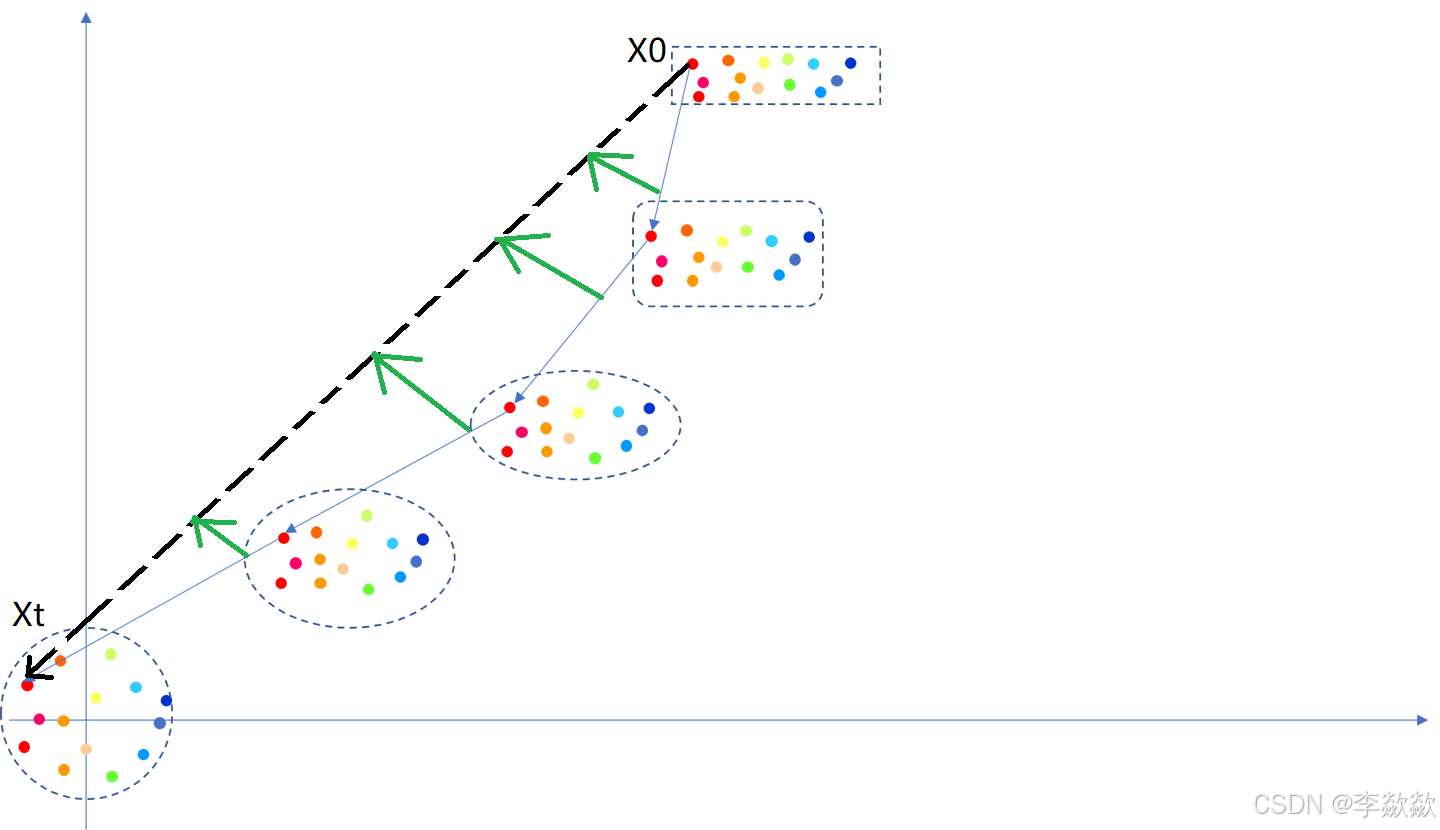
在这里插入图片描述
上面介绍的是直线路径的RF，那么分段式路径的RF只需要将直线分成多段即可，如下图：