割平面法（Cutting Planes ）

有效不等式 （Valid Inequalities）、 割平面（Cutting Plane）算法

（1）最可能的结果和理想约束都是由提供

（2）目标：通过给定的已知条件，找到有效方法来近似获得

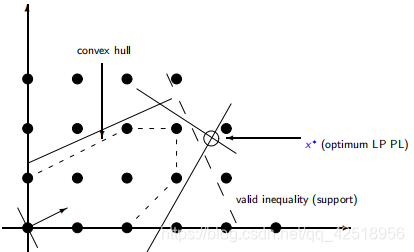
（3）通过生成线性不等式（所有整数解均满足）来加强约束，这种不等式称为有效不等式

定义6：对于所有均满足。那么对于，不等式是一个有效不等式

      其中，有效，当且仅当X落在半平面中

             

（1）0-1背包问题

                         

                （a） 如果，那么（不成立），因此

                （b） 如果，那么（x3,x5取0，x4取1）,因此（x1不大于x2,）（1,1；0,1；0,0）

（2）混合整数集

                        （x 为 连续值， y 为整数）

                    

                               其中不等式是有效的，并提供了X的凸包

（3）近似（Rounding ）

     

        （a） 对三个约束 使用进行线性组合

                      

        （b）  对一些系数进行降低（reducing），或者使用替代（substituting）

                      （将1/2 用“0” 代替，因为都为正整数，所以变为小于号）

        （c） 左端项为整数，因此右端项必然

                        每个变量均为正整数，可以将3/2 改为“1”

        （d） 最终的不等式变为：，  切掉了LP问题的最优解

生成有效不等式的方法

（1）如果是可行整数解集，并且是问题约束的线性松弛的可行域，那么除非（P为所有整数解X的凸包），那么存在有效不等式对于有效，但不满足P。（包含凸包的更小可行域）

（2）生成有效不等式的方法：

             （a）近似（rounding）

             （b）模运算（Modular arithmetic ）

             （c）混合整数近似（Mixed integer rounding）

             （d）吸取（Disjunctions）

             （e）添加（Superadditivity）

Rounding:

（1）此方法基于下面两个现象：

             （a） 如果，，那么  （x取不大于a的最大整数，向下取整）

             （b） 如果 包含X的有效不等式，且，那么对于依然有效 （等式两边同时乘以一个大于“0”的数，不等式不变号）

（2）令 为矩阵的列，且

                         

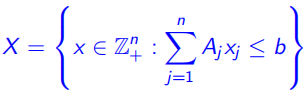
定义7（有理多面体，Rational Polyhedron）：如果存在一个带有合理系数的大小的矩阵使得，那么这个多面体是有理的（rational ）

Chv´atal-Gomory Procedure

（1）选择，并计算矩阵行的一个线性组合：

                    

（2） 将系数向下取整（Round down）：

                   

（3） 将右端项向下取整（Round down）：

                   

通过改变，我们得到第一个Chv´atal 封闭多面体  ：

               

的线性描述

定理1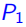：是一个多面体

给定是一个有理多面体，可以再次对使用近似（rounding）操作，从而得到

从而可以得到一系列的多面体：

     

定理2：对于每个有效不等式可以使用Chv´atal-Gomory操作在有限次后得到

定理3：令为一个有理多面体，那么我们可以得到，对于

定义8（Chv´atal 的秩）：为一个有理多面体，Chv´atal 的秩为最小整数k，使得在第k次得到凸包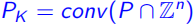

图的匹配问题

（1）对于图，匹配（matching）是不相连的边（disjoint edges）的集合，

          比如，每个子图中的节点，不出现在第二条边上