0、Abstract
主要研究问题：balanced connected k-partition problem
问题描述：给定一个图 G = (V, E)，每个节点权重均非负（nonnegative），将节点集合V划分成 k个子集，使得每个子集都是G中的连通子图，权重最小的子集权重 越大越好（with the minimum weight is as large as possible）。
贡献：对
提出三种线性规划建模
（1）只包含 0-1变量，以及大量约束
其中约束对应的线性松弛可以在多项式时间内被分解（a potentially large number of constraints that can be separated in polynomial time in the corresponding linear relaxation）
（2、3）基于arc-flow建模，并且具有多项式个数的约束条件和变量
1、Introduction
[k] 表示集合 {1, 2, . . ., k}， k>=1 表示非空集
G 的 k-partition 也就是 的集合 ，其中 所有子集的并集是 V的全集，子集间无交集，即
表示由 产生的每个子图
均是连接图
：为G中每个节点分配非负权重的函数
对于每个子集
，
对于每个子图 H 使用 
表示子图权重，而不是
对于可行解集
，使用
表示 S 的凸包（convex hull）
Problem 1. Balanced Connected k-Partition (BCPk)
与之相对的还有
，用来 minimizes 
1.1、Some known results
unweighted BCPk (1-BCPk)：每个节点都是单位重量
（1）unweighted BCPk 在二分图（bipartite graphs，节点可以分成两个不相交的集合，使得任意集合内节点不相邻）在
是 NP难问题
（2）BCP2 （节点带重量）在 grid graphs 上也是 NP难问题
（3）Chlebíková (1996) 4/3-approximation 求解 BCP 2
（4）Chen et al. (2020) 5/3-approximation 求解 BCP 3
3/2-approximation 求解min-max BCP3 on arbitrary graphs
（5）估计算法（Approximation）BCP4 on 4-connected graphs 或者 1-BCPk on special classes of graphs
（6）Wu (2012) fully polynomial-time approximation scheme (FPTAS) for BCP2 on interval graphs
（7）Borndörfer, Elijazyfer, and Schwartz (2019) 使用 △-approximation 求解 max-min and min-max 两种问题，△ 是图G 中任意至支撑树的最大度（maximum degree of an arbitrary spanning tree），特别是max-min 中，将限制最大权重在 
内，
（8）Chataigner et al.(2007) 证明 BCPk问题 不能估计比率高于 6/5的
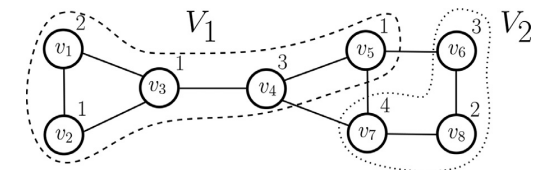
2、Cut-based formulation
使用 ILP 对BCP 建模称为 
假设 u 和 v 是两个 在图G 中不相邻的连个点，定义 
是一个 (u,v)-separator，当 u 和 v 属于 G - S的两个部分。其中 
是 (u,v)-separator 中 点数最少的集合
约束：
（1）重量升序
（2）最多只属于一个集合
（3）如果u,v在同一 集合 i 中，至少包括一个分割点
分析：
对于约束（2），可能导致部分点没有分配到任何一个集合，此时存在一个
是G的k个连接子图，并且重量递增，使用贪婪策略，将未分配的节点放入某个与它相邻且已放入非空集合的节点的集合，每次都从距离为1的节点开始放起（部分节点的相邻节点可能也未分配）
定义
，
表示节点 v已经分配给集合 i ，其对应可行域的多面体被定义为：
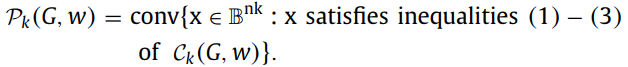
下面是对模型的加强：
Proposition 1.
证明：
考虑极点
定义节点集合
（已经分配在 集合 i 的所有 v），当满足不等式（1）、（2），那么
已经是G的子图的k个部分（可能有节点未选中，并不是全集），并且集合总重升序排列
证明 u 是一个connected k-subpartition：
反证法：假设存在一个 G[Ui]不是连接图，一定存在节点u v属于G中两个不同部分，因此存在 minimal (u,v)-separator S （没有连接的区域）使得
，这与约束3是矛盾的
正向证明：对于G中的connected k-subpartition，每个
局满足约束（1）（2），对于任意集合i 中的两个不相邻节点 u v ，一定会存在(u,v)-separator S 并存在
，从而满足不等式3。
Proposition 2.
令 S 为 minimal (u,v)-separator，
，
是G中包含点 z 使得u-v相连的最小权重路径（minimum-weight (u,v)-path）
提出以下约束：
证明：
取
，
，j 为 集合{1...k} - {1... i-1}，最终得到索引 从 i - k，于是得到：
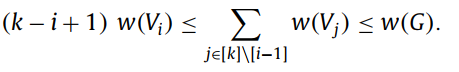
由于 集合总重递增， 集合 i 重量均小于等于 i+1 - k 集合的总重，于是得到
为集合i 总重的上界（upper bound）
因此只要存在一个
（Z是会超过上界的点需要排除），那么将满足约束（5）即形成连通图
Proposition 3.
本约束是从connected assignment problem收到启发，
定义
是一个固定整数，S为G的一个顶点子集，包括q对不相邻节点（distinct pairs）
，并且对于对之间彼此不相邻（mutually disjoint），令N(S) 为集合 V \ S 内 与S相邻的节点集合，
为一个映射函数（injective function），
如果在G[S]中没有q组不相连路径的集合，那么下面不等式成立：
证明：
反证法：如果
中存在一个极点违背了约束（6），
令
以及
由约束（2）可得
（部分点未分配集合），由于整体违背约束（6）那么
（带入约束6推出），又因为满足约束（2）使得每个节点最多分配在一个集合，因此通过上下界确定
因此得到，N（S）的点均不属于索引值为 I 的集合（相邻点均不属于相同集合，那么这些集合均将被独立），于是每一个 I 对应的集合都准确对应q对不相邻点中的一对，因此在图G【S】中存在q组不相邻点的路径集合
3. Separation algorithms
3.1. Connectivity inequalities
问题：对于约束（3）这种连接约束，其分解问题（separation problem）为：给定向量
，找到 
违背的约束，或证明这个向量满足所有约束
给定输入G = (V, E)，定义有向图
节点容量为
：使用
为每条边分配重量，将每个节点都复制一份 
，
相应弧权重更新：
， 节点之间的弧
， 节点内部的弧
为属于节点内部的弧，初始化为 变量值，
分析：
对于任意不相邻节点 u,v 如果
，将会在
中找到minimum (u1,v2)-separating cut， 如果这种cut 的总重小于
，那么将违背约束（5）
，
假设
为 S，
为 G - S 中 包含 u 的部分，下面将迭代对连接约束使用 lifting 从 S 中移除无效点：
（1）移除 S 中 那些 邻点集合与
无交集（intersect）的点，由于S 发生变化，使用 Union-Find 数据结构来更新检测点集合
（2）根据 Proposition 2.使用 Dijkstra’s algorithm 移除 S中的 Z（不在界内的路径）
时间复杂度：
分解连接约束的时间复杂度取决于查找最小割（minimum cut）的算法，本文使用 maximum flow Goldberg and Tarjan (1988)，时间复杂度为
，对于最坏情况，分解算法的时间复杂度为
实际结果中 分数解很少，因此对所有弧进行 arc contractions，即对其端点都设置为整数，比如，
收缩为：
，
收缩为：
3.2. Cross inequalities
现在在平面图（planar graphs）上对约束（6）进行分解，假设 F 为图中一个至少4个点的face，并且没有重复节点，按顺时针方向，记作
，由于图是平面的，不应该包含两个不相邻节点的路径，如
（会产生交叉！），如果此时对于约束（6），集合 S = V（不存在N（S）），那么有
，这个被称为交叉不等式（cross inequalities）
本文使用方法复杂度在
，使用方法为 Barboza (1997)
分解算法：
本节中，节点均在图F内，并且节点个数为
，假设
为一个分数解，先对于图上点按顺时针顺序从任意固定点遍历，对于每个
定义
为图中第 j 个顶点，并以 j 为中心在其左右分别对每个
统计最大量，其中：
出 j = 1外，对于每个 
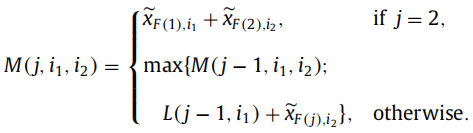
为 前 j 项中两个递增项，
，中 
的最大值。 对于
，我们将判断
， 从而判定是否有存在 交叉约束
注： 其中 M 用来找到 前 j - 1项中，可能存在的 i1,i2的最大值，第三项为 j 项 属于 i1 的取值，最优一项为 j + 1项到最后 属于 i2的值。加和起来为约束（6）判定式
4. Flow-based formulations
本节将 BCPk 的 MILP 问题 以有向图的 flow进行建模
无向→有向变换：
（1）G中的每条边，都分成相同端点的两个相反方向的弧
（2）添加集合
，用来表示不同集合的源点（source），并添加从S到G中所有节点的一条弧，
输出：节点集合： 
弧集合：
输入： 每条弧
，非负流量
，指示变量
（
）
表示 集合A’中所有选中的边数：
约束（7）：各集合总重为非降序
约束（8）：流平衡约束，对于每个点，输入流的和 - 节点v 消耗量 = 输出流量
约束（9）：弧 a 是否被选中
约束（10）：每个源点 s 只能流向一个节点
约束（11）：每个节点只能流向 一个节点
注：如果节点中包含重量为“0”的节点，可能会不接收到流量，这种情况归并到距离为“1”且已经归类的集合中，此时并且不会影响任何集合的总重。
总结：本方法共使用2nk + 4m（一半为0-1变量）个变量，对于 n 各节点，m条边，k个集合 复杂度为
缺点：存在大量对称结，并依赖约束（9）对节点分配权重
改进方法：该模型考虑顶点的总顺序，以避免对称，并将分配给顶点的权重从有向图中循环的流（flow circulating）中解耦（uncouples）。
4.1 Asymmetric flflow-based formulation
定义：使用单个源点 s
使用 顺序符号
定义顺序
定义每个集合 i 通过边 a 的量
为 集合 i 包括的节点，其子树为
，具体为：
（1）其根节点为 从 s传递过来的
个流
（2）根节点将消耗一个流后 继续向后传递 
（3）最终叶节点 接收一个单位流后 结束
（4）通过定义 root 为最小顺序，来打破对称性（breaking symmetries）
、
同样定义
，表示fa,i非空，
表示 集合 A'内所有选中点的个数 
令 
为 G中的 k个连接部分，可以得到
对于根节点在
的子树
，已知 总流量
，并且
即，根节点重量（顺序）最小
对于赋值函数
，如果
，证明 v是叶节点（末尾），其余的为 
，并且从源点s分到的 总量是
现定义两变量 指示变量 
，重量变量 
Proposition 4. 多面体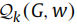
就是原问题解空间
：v是G的k个连接部分
证明：
令(y, f) 为
的一个极点，令
，约束（15）保证每个集合 i 中，最多只有一条弧能离开源点s，因此每个
都是 G的k个连接部分。
约束（16）保证每个节点v只能被输入一条弧，约束（18）表示只能从有弧的变量选择
约束（19、20）保证输入输出流来自同一集合 并且 只消耗一个单位流
反推：
已知 
是 G中的 k 个连接部分，且重量递增
令
表示 
，
，对于每个集合
，
的入度最多为“1”，其根节点
为子树中的最小节点（对于顺序
），
约束（16、17） 保证对于其中的最小 u ， 更高顺序的节点v 不会是 承接 s的节点。
因此，满足约束（15）即每个节点 发出一条弧。
5237
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
