TPAMI 2024 | MoIL: 基于动量模仿学习的视觉-语言高效适应方法

论文信息

题目：MoIL: Momentum Imitation Learning for Efficient Vision-Language Adaptation

MoIL: 基于动量模仿学习的视觉-语言高效适应方法

作者：Gen Luo, Yiyi Zhou, Minglang Huang, Tianhe Ren, Xiaoshuai Sun, Rongrong Ji

源码链接：https://github.com/luogen1996/MoIL

论文创新点

1. 动量模仿学习：提出动量模仿学习方法，直接优化低秩适应的近似误差，显著提高VLP模型的优化效率。
2. 混合近似函数：引入混合近似函数，结合线性适配器和LoRA，进一步降低低秩适应的学习难度。
3. 高效参数更新：通过仅更新少量参数，MoIL在多个VLP模型和任务上实现了与全微调相当的性能，同时保持高效推理和泛化能力。

摘要

预训练和微调已成为视觉-语言领域的标准范式。随着模型规模的快速增长，完全微调这些大规模视觉-语言预训练（VLP）模型需要极高的存储成本。为了解决这一问题，自然语言处理（NLP）领域的最新进展提供了一种有前景且高效的适应方法，称为LoRA，旨在通过更新低秩参数来近似大规模预训练模型的微调。尽管LoRA有效，但作者发现其在VLP模型上存在较大的近似误差，且优化效率较低，这大大限制了其性能上限。在本文中，作者通过数学证明，低秩适应的近似误差可以通过一个新的优化目标进行优化，即LoRA与微调之间的权重距离。基于这一发现，作者提出了一种新的VLP模型PETL方法，称为动量模仿学习（MoIL）。具体来说，MoIL将PETL视为一个权重模仿学习过程，并直接优化低秩适应的近似误差边界。基于这一训练方案，作者还探索了一种新的混合近似函数，以降低低秩适应的学习难度。通过这两个新颖的设计，MoIL可以显著提高VLP模型上低秩参数的优化效率。作者在三个VLP模型上验证了MoIL，并在四个VL任务上进行了广泛的实验。实验结果表明，MoIL在性能和优化效率上均优于现有的PETL方法。例如，通过仅更新6.23%的参数，MoIL在图像-文本匹配任务上甚至可以比全微调高出+2.3%。同时，其推理效率和泛化能力也在多个VLP模型（如VLMO和VinVL）上得到了验证。作者的源代码可在以下网址获取：https://github.com/luogen1996/MoIL。

关键字

• 参数高效迁移学习
• 视觉-语言预训练

1 引言

近年来，基于数百万图像-文本数据的预训练已成为视觉-语言学习的标准范式。借助大规模预训练知识，基于Transformer的视觉-语言预训练（VLP）模型可以获得优于定制模型的多模态表示和对齐，从而在视觉问答（VQA）、图像描述生成（IC）和图像-文本匹配（ITM）等任务中占据主导地位。作为对比，这些VLP模型通常需要大量的参数来适应庞大的预训练数据，这使得它们在下游任务中的适应成本极高。例如，完全微调VLMO-large在4个VL任务上消耗了超过20亿个参数。

NLP领域的最新进展提供了一种潜在的解决方案，即参数高效迁移学习（PETL）。PETL方法的主要原理是仅更新或插入少量可训练参数以适应下游任务，从而避免昂贵的全局参数更新。尽管现有的PETL方法在NLP任务中表现出竞争力的迁移学习性能和显著的参数效率，但大多数方法在推理过程中仍会产生不可忽视的计算开销。例如，适配器会使得ViLT的推理速度降低高达35.1%。

目前，一个可行的解决方案是Hu等人提出的重参数化方法，称为低秩适应（LoRA）。LoRA的假设是，大规模预训练模型的微调通常具有较低的内在维度。在这种情况下，LoRA可以使用低秩分解矩阵来近似预训练模型的密集层参数更新。理想情况下，如果LoRA的近似误差较小，它可以达到与全微调相当的性能。同时，LoRA的低秩权重可以在训练后重新参数化到模型中，从而在推理过程中不产生额外成本。尽管LoRA保持了高计算效率，并在各种NLP任务中获得了与许多PETL方法相当的性能，但作者发现LoRA在VLP模型上会遭受较大的近似误差，且其优化效率较低。

具体来说，VLP模型的预训练目标（如掩码语言建模）通常与下游任务（如VQA）存在较大差距。这种差距会大大增加LoRA的近似难度。在实践中，作者发现LoRA与微调之间的权重距离可以衡量其近似误差，这在VQA任务上实际上很大。同时，LoRA的训练目标是最小化预测与真实标签之间的差异，这对于优化近似误差来说是间接且低效的。因此，LoRA的训练曲线始终不如微调，如图1所示。

在本文中，作者发现低秩适应的近似误差可以通过一个新的优化目标进行优化，即LoRA与微调之间的权重距离。基于这一发现，作者提出了一种新的VLP模型PETL方案，称为动量模仿学习（MoIL）。如图1所示，MoIL通过模仿微调权重直接优化权重距离。在实践中，作者直接微调预训练模型中的一小部分权重，并最小化适应权重与微调权重之间的l2距离。同时，作者进一步提出了一种动量更新策略，以提高模仿学习的稳定性，该策略采用微调权重的指数移动平均作为模仿目标。除了这一训练方案外，作者还提出了一种新的混合近似函数，以进一步降低低秩适应的学习难度。通过这些新颖的设计，MoIL可以显著提高下游VL任务的优化效率。

为了验证MoIL，作者将其应用于三个VLP模型（ViLT、VLMO和VinVL），并在四个VL任务的六个基准数据集上进行了广泛的实验。实验结果表明，MoIL在三个VLP模型上均优于现有的PETL方法，例如在ViLT上平均提升+1.0%，同时在推理过程中保持高效。同时，作者进行了一系列消融研究和泛化实验，验证了MoIL的有效性和效率。总结来说，作者的贡献有三点：

1. 作者发现了将LoRA应用于VLP模型时存在较大的近似误差问题，并提出了一种新的PETL框架。据作者所知，这是第一个用于适应常见VLP模型的PETL方法。
2. 为了解决这一问题，作者提出了一种新的PETL方法，称为动量模仿学习（MoIL），并结合了混合近似函数，可以显著提高优化效率。
3. MoIL在四个VLP模型和六个VL任务上优于现有的PETL方法。此外，MoIL在推理和优化效率上也优于现有的PETL方法。

3 方法

3.1 预备知识

作者首先回顾了流行的PETL方法LoRA，然后分析了LoRA的近似误差。

LoRA
LoRA旨在在VLP模型中插入并更新低秩参数$\delta$以适应下游任务。LoRA的动机是，大规模预训练模型的微调具有较低的内在维度，因此更新少量低秩参数可以近似全微调的性能。具体来说，给定VLP模型的预训练权重$W_0\in {\mathbb{R}}^{d\times d}$，LoRA可以表示为：

$$\varphi (\delta )=W_0+\delta =W_0+AB$$

其中，$A\in {\mathbb{R}}^{d\times r}$和$B\in {\mathbb{R}}^{r\times d}$是两个低秩权重。在训练过程中，$W_0$被冻结，仅更新$AB$。训练后，$AB$可以重新参数化到$W_0$中，从而在推理过程中不产生额外成本。在实践中，LoRA仅部署在多头注意力层的投影权重中，即$W_Q$、$W_K$和$W_V$。对于不同的下游任务，作者仅存储低秩权重$AB$，从而大大减少了存储成本。

尽管LoRA有诸多优点，但作者关注的是LoRA是否能实际近似全微调。为了回答这个问题，作者回顾了LoRA和全微调的优化过程。作者首先定义了Lipschitz连续性，这将在证明中使用。

定理1（Lipschitz连续性）：给定一个函数$f:{\mathbb{R}}^n\to {\mathbb{R}}^m$，如果存在一个常数$L>0$，使得

$$\Vert f(x)-f(y){\Vert }_p\le L\Vert x-y{\Vert }_p$$

则称$f$是Lipschitz连续的，其中$L$是Lipschitz常数，$p$表示$p$-范数，通常设置为2。

设$\tilde{L}(\theta ,\delta )$和$\mathcal{L}(\theta )$分别表示PETL和全微调的目标函数。这里，$\theta$和$\delta$分别是VLP模型和LoRA的参数。训练从${\theta }_0$和${\delta }_0$开始，其中${\theta }_0$和${\delta }_0$分别表示预训练权重和$\delta$的初始化。${\delta }_0$可以初始化为零，例如LoRA，因此可以得到：

$$\underset{\theta ,\delta }{\min }\tilde{L}(\theta ,\delta )\le \underset{\theta }{\min }\tilde{L}(\theta ,{\delta }_0)=\underset{\theta }{\min }\mathcal{L}(\theta )$$

$$\underset{\theta ,\delta }{\min }\tilde{L}(\theta ,\delta )\le \underset{\delta }{\min }\tilde{L}({\theta }_0,\delta )$$

从公式3可以看出，联合微调预训练VLP模型和PETL方法的参数将达到最佳结果。然而，作者只对PETL和全微调之间的差距感兴趣，即$|\tilde{L}({\theta }^{+},{\delta }_0)-\tilde{L}({\theta }_0,{\delta }^{+})|$。设${\theta }^{+}=\arg {\min }_{\theta }\tilde{L}(\theta ,{\delta }_0)$和${\delta }^{+}=\arg {\min }_{\delta }\tilde{L}({\theta }_0,\delta )$，并假设$\tilde{L}$是二次Lipschitz连续可微函数，可以证明：

$$|\tilde{L}({\theta }^{+},{\delta }_0)-\tilde{L}({\theta }_0,{\delta }^{+})|=\mathcal{O}(||{\theta }^{+}-{\theta }_0|{|}_2^2+||{\delta }^{+}-{\delta }_0|{|}_2^2)$$

公式4描述了PETL和全微调之间存在差距，这也意味着LoRA与全微调之间仍然存在近似误差。接下来，作者给出了近似误差的边界分析，这决定了LoRA的有效性。

LoRA的近似误差
具体来说，Aghajanyan等人发现$\theta$的优化近似于一个流形。基于LoRA的假设，隐藏流形可以通过$\theta =\varphi (\delta )+ϵ$嵌入到低维空间中，其中$ϵ$是误差项，$\varphi$是LoRA的近似函数。然后，LoRA的优化目标可以写为：

$$\tilde{L}({\theta }_0,\delta )=\mathcal{L}(\varphi (\delta ))$$

这里，${\theta }_0$表示预训练权重。作者的目标是找到LoRA的近似误差边界，即$|\mathcal{L}({\theta }^{+})-\mathcal{L}(\varphi ({\delta }^{+}))|$，其中${\delta }^{+}=\arg {\min }_{\delta }\mathcal{L}(\varphi (\delta ))$和${\theta }^{+}=\varphi ({\delta }^{\prime })+{ϵ}^{\prime }$。假设$\mathcal{L}$和$\mathcal{L}\circ \varphi$是Lipschitz连续的，且Lipschitz常数分别为$L_1$和$L_2$，则近似误差的边界可以写为：

$$|L({\theta }^{+})-L(\varphi ({\delta }^{+}))|\le L_1\Vert {ϵ}^{\prime }{\Vert }_2+L_2\Vert {\delta }^{\prime }-{\delta }^{+}{\Vert }_2$$

这里，${ϵ}^{\prime }$是误差项，其实际上非常小。因此，LoRA的有效性依赖于$\Vert {\delta }^{\prime }-{\delta }^{+}{\Vert }_2$，即LoRA与全微调在低秩空间中的权重距离。这意味着如果${\delta }^{\prime }-{\delta }^{+}$的幅度较小，LoRA可以获得良好的近似结果。然而，由于预训练目标与下游任务之间的差距较大，VLP模型上的近似误差实际上很大。尽管如此，LoRA的训练目标是最小化预测与真实标签之间的差异，这对于优化近似误差来说是间接且低效的。如图1所示，训练过程中$\Vert {\delta }^{\prime }-{\delta }^{+}{\Vert }_2$的值并未有效减少，表明直接用LoRA近似全微调在VLP模型上仍然困难。

3.2 MoIL

3.2.1 动量模仿学习

权重模仿学习：如上所述，由于较大的近似误差，LoRA在VLP模型上的性能会落后于全微调。为了找到最优的${\delta }^{+}$，一个自然的解决方案是最小化$\Vert {\delta }^{\prime }-\delta {\Vert }_2$，即${\delta }^{+}=\arg {\min }_{\delta }\Vert {\delta }^{\prime }-\delta {\Vert }_2$，从而得到权重模仿学习的优化目标。具体来说，优化目标可以写为：

$$L_{imi}=\Vert {\delta }^{\prime }-\delta {\Vert }_2=\Vert {\theta }^{\prime }-(\delta +{\theta }_0){\Vert }_2=\Vert {\theta }^{\prime }-\varphi (\delta ){\Vert }_2$$

在公式7中，$L_{imi}$旨在最小化适应权重与微调权重之间的距离。为了确保在训练过程中可以优化，作者需要通过下游任务目标$L_{task}$来更新${\theta }^{\prime }$。因此，模仿学习的总体目标可以定义为：

$$L=L_{task}+\lambda L_{imi}$$

这里，$\lambda$是调整$L_{imi}$权重的超参数。在训练过程中，${\theta }^{\prime }$和${\delta }^{\prime }$的优化是并行且独立的，具体过程如算法1所示。在实践中，作者仅选择VLP模型中的一小部分参数进行模仿学习，这不会显著增加训练成本。在开发过程中，作者仅存储轻量级的适应权重${\delta }^{+}$，以保持参数高效。与直接采用微调参数相比，这些轻量级的适应权重将大大减少存储成本。在这种情况下，权重模仿学习可以在性能和效率之间实现良好的平衡。

如图2所示，作者在MSA层中采用了模仿学习。具体来说，作者使用重新参数化的权重$\varphi ({\delta }_Q^{\prime })$、$\varphi ({\delta }_K^{\prime })$和$\varphi ({\delta }_V^{\prime })$来模仿注意力权重的更新，即$W_Q^{\prime }$、$W_K^{\prime }$和$W_V^{\prime }$。在这种情况下，VLP模型的模仿学习损失定义为：

$$L_{imi}=\Vert W_Q^{\prime }-\varphi ({\delta }_Q^{\prime }){\Vert }_2+\Vert W_K^{\prime }-\varphi ({\delta }_K^{\prime }){\Vert }_2+\Vert W_V^{\prime }-\varphi ({\delta }_V^{\prime }){\Vert }_2$$

在实践中，作者观察到不同训练步骤中的微调权重（如$W_Q^{\prime }$）变化迅速，这会损害学习的稳定性。为了解决这个问题，作者进一步提出了一种动量更新策略。

动量更新：动量更新旨在使用不同训练步骤的平均权重作为模仿目标，从而提高学习的稳定性。具体来说，给定第$k$个训练步骤的参数$\theta$，其动量更新可以表示为：

$${\hat{\theta }}_k\leftarrow \alpha {\hat{\theta }}_{(k-1)}+(1-\alpha ){\theta }_k^{\prime }$$

其中，$\alpha$是动量系数。动量更新使得权重变化更加平滑。在这种情况下，不同步骤的模仿目标将相对相似，从而大大降低了学习难度。如目标检测中所述，这种动量学习可以帮助缓解过拟合问题，这对于VL适应也非常重要。通过动量更新，VLP模型的模仿学习损失可以重写为：

$$L_{imi}=\Vert {\hat{W}}_Q^i-\varphi ({\delta }_Q){\Vert }_2+\Vert {\hat{W}}_K^i-\varphi ({\delta }_K){\Vert }_2+\Vert {\hat{W}}_V^i-\varphi ({\delta }_V){\Vert }_2$$

值得注意的是，尽管动量模仿学习需要微调部分模型参数，但它仍然可以保持与LoRA相似的训练效率。原因有三点：首先，MoIL仅微调少量模型参数，其计算成本已经比全微调便宜得多。其次，作者的动量模仿学习每五次迭代进行一次，进一步减少了训练时间。其次，模仿学习的成本在理论上也很低，梯度可以直接从更新的模型权重中获得，因此不需要额外的深度反向传播。第三，作者的混合适应结构轻量且高效，将在第3.2.2节中描述。

3.2.2 混合近似函数

作者接下来介绍混合近似函数，以提高优化效率。LoRA的近似函数定义为$\varphi (\Delta W)=W_0+\Delta W$。Ding等人认为，对$W_0$应用适当的变换$S$可以降低优化难度。受此启发，作者提出了一种混合近似函数，表示为${\varphi }_h(S,\Delta W)=S{W}_0+\Delta W$，由一个变换项和一个偏置项组成。与LoRA类似，混合近似函数也通过适应模块的重新参数化获得。为此，作者首先介绍其结构，然后描述其重新参数化。

混合适应结构：如图2所示，给定输入特征$X\in {\mathbb{R}}^{1\times d}$，变换适应模块定义为：

$$f_t(X)=X+(X{A}_d+a_d)B_d+b_d$$

其中，$A_d\in {\mathbb{R}}^{d\times d}$和$B_d\in {\mathbb{R}}^{d\times d}$是投影权重，$a_d\in {\mathbb{R}}^d$和$b_d\in {\mathbb{R}}^d$是偏置项。变换适应模块的公式接近适配器，但去除了非线性。偏置适应模块可以写为：

$$f_b(X)=X{W}_0+X{A}_b{B}_b$$

这里，$W_0\in {\mathbb{R}}^{d\times d}$是预训练模型中的冻结权重。作者在偏置适应模块之前插入变换适应模块。在这种情况下，整个结构可以最终重新参数化为$W_0$。具体来说，混合适应结构可以表示为：

$$f_h(X)=f_b(f_t(X))$$

混合适应结构可以看作是线性适配器和LoRA的组合，可以在优化中提供正交的改进。如图2所示，混合适应结构也部署在MSA层中。

重新参数化：作者接下来通过重新参数化获得近似函数，如图3所示。具体来说，适应结构的定义可以重写为：

$$f_h(X)=f_a(f_t(X))=X(W_0+A_d{B}_d{W}_0+A_b{B}_b)+a_d{B}_d{W}_0+b_d{W}_0$$

为了简化，作者忽略偏置项$a_d{B}_d{W}_0+b_d{W}_0$，新的近似函数定义为：

$${\varphi }_h(S,\Delta W)=(I+A_d{B}_d)W_0+A_b{B}_b=S{W}_0+\Delta W$$

这里，$I$表示单位矩阵。在推理过程中，重新参数化也可以将适应模块合并到冻结权重中，从而在推理过程中不产生额外成本。因此，作者的方法比大多数现有的PETL方法更高效。

4 实验

4.1 数据集和指标

视觉问答（VQA）：作者在三个数据集上评估VQA任务，分别是VQA2.0、NLVR2和GQA。具体来说，VQA2.0包含1.1M人类标注的QA对，用于200k MS-COCO图像，分为训练、验证和测试集，分别包含80k、40k和80k图像。与VQA2.0相比，NLVR2旨在对语言偏差具有鲁棒性，包含107k QA对用于214k图像。NLVR2的训练、验证和测试集分别包含86k、7k和7k样本。GQA包含113k图像和22M QA对，其中70%、10%和10%的样本分别划分为训练、验证和测试集。作者在实验中报告VQA分数、GQA分数和NLVR分数。

图像-文本匹配（ITM）和图像描述生成（IC）：作者在Flickr30k和MS-COCO上进行ITM实验，并在MS-COCO上评估IC。具体来说，Flickr30k包含31k图像和155k文本描述，分为训练、验证和测试集，分别包含29k、1k和1k图像。MS-COCO包含8k、5k和5k图像，分别用于训练、验证和测试集。对于每个图像，有五个文本描述。对于图像-文本匹配，作者报告图像检索和文本检索的top-1召回率，分别表示为IR@1和TR@1。对于图像描述生成，作者报告CIDEr分数。

4.2 VLP模型

ViLT：ViLT是第一个没有大型视觉骨干网络和语言编码器的统一VLP模型。输入图像和文本通过补丁投影和BERT分词器直接处理，并输入到12层Transformer中进行多模态交互。ViLT的模型维度为768。

VLMO：VLMO也遵循统一结构。与ViLT不同，它引入了多模态专家Transformer，可以有效处理不同模态。得益于该结构，VLMO可以在图像数据、文本数据和图像-文本数据上进行预训练。在执行图像-文本匹配任务时，它也可以像CLIP一样作为双流模型。在本文中，作者在VLMO-B上验证了方法，其中层数和维度分别为12和768。

VinVL：VinVL遵循两阶段流水线，其中视觉特征和文本特征分别由Faster-RCNN和BERT提取。作者在VinVL-B上进行实验，该模型包含12层Transformer，维度为768。

4.3 实现细节

VLP模型的微调超参数遵循其论文中的默认设置。默认情况下，作者仅将适应模块应用于多模态融合网络。对于Prompt tuning、Adapter和LoRA，作者冻结所有参数，除了分类器和适应模块。对于MoIL，MSA的投影权重也进行微调以进行模仿学习。同时，作者在微调中移除了数据增强，这会损害模仿学习的过程。其余超参数保持不变。为了更好地适应现有的PETL方法到VLP模型，作者还进行了一些修改。

MoIL：作者将MoIL应用于MSA的三个投影权重，即$W_Q$、$W_K$和$W_V$。MoIL的适应模块维度设置为96。$A_d$和$A_b$初始化为均匀分布，其余权重初始化为零。

4.4 实验结果

4.4.1 性能比较

ViLT上的性能比较：在表1和图4中，作者展示了不同微调方法和现有PETL方法的性能。从表中可以看出，仅微调头部（Head Only）在四个VL任务上的性能较差，并且在VQA和NLVR2上导致更明显的性能下降，例如在NLVR2上下降了-11.9%。通过微调LayerNorm，下游任务的性能显著提高，但仍落后于全微调。这些结果表明，除了数据分布外，预训练和微调之间存在较大的任务特定差距。在这种情况下，直接微调MSA层可以更好地适应下游数据分布和任务目标，从而在所有微调方法中实现最佳性能。令人惊讶的是，仅微调MSA层在ITM任务上甚至可以优于全微调，例如在COCO上的IR@1提高了+2.5%。与仅微调MSA层相比，仅微调FFN层使用了更多的参数，但性能较差，例如平均性能下降了-0.5%。这些结果很好地支持了作者关于适应VLP模型挑战的动机。

与这些微调方法相比，现有的PETL方法更具参数效率。具体来说，Prompt tuning显著提高了仅微调头部的平均性能，例如在VQA上提高了+7.5%。与Prompt tuning相比，Adapter和LoRA展示了更强的适应能力。例如，Adapter在ITM任务上可以实现与全微调非常接近的性能，例如在COCO上的IR@1为45.0，而LoRA的平均性能略优于Adapter，即+0.2%。然而，作者也观察到，与全微调相比，这些方法在VQA任务上仍存在较大的性能差距，例如Adapter在NLVR2上下降了-3.7%。相比之下，MoIL在VQA任务上展示了更强的适应能力，并实现了与全微调接近的性能，例如在VQA上的70.9 vs 71.2。在两个ITM任务上，MoIL也显著优于全微调，例如在COCO上的IR@1提高了+2.3%。这些结果很好地验证了MoIL的有效性。

在图4和表7中，作者比较了MoIL和现有PETL方法在不同参数规模（秩）下的性能。从图4中可以看出，随着更新参数的增加，所有方法在四个数据集上的性能都有所提高。这一结果也反映了适应VLP模型的挑战，通常需要比语言预训练模型更多的适应参数。与其他PETL方法相比，MoIL可以在性能和参数之间实现更好的权衡。例如，MoIL在较小的秩（3.5M参数）下可以优于LoRA在较大秩（14M参数）下的性能。类似的结果也可以在表7中看到，MoIL在秩从8到96的范围内均优于LoRA。从表中还可以注意到，在预训练目标与下游任务差距较大的任务（如VQA）中，LoRA和MoIL需要更大的秩才能达到与全微调相当的性能。这是因为较小的秩在最小化这些任务中的近似误差方面能力有限。在实践中，秩为96提供了所有任务中性能和效率的最佳权衡。这些结果不仅展示了秩对MoIL和LoRA的影响，还确认了MoIL比LoRA具有更优越的参数效率。

4.4.2 与微调基线的比较

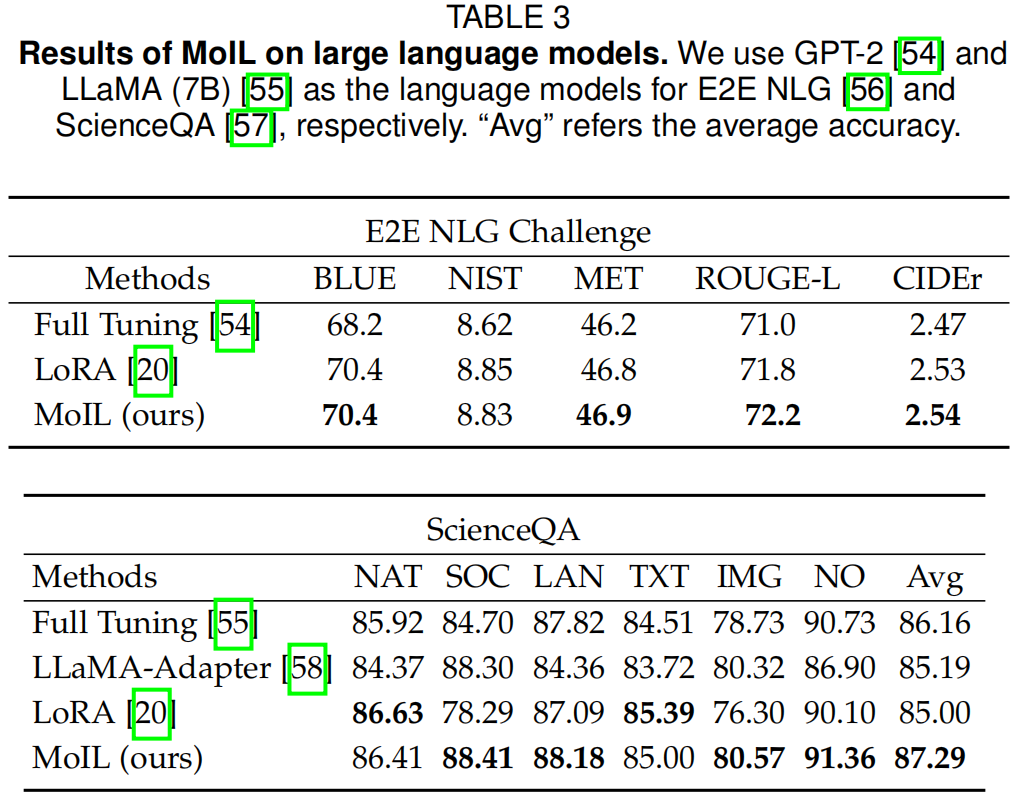
在表3、4、9、8和10中，作者全面比较了MoIL与微调基线（部分微调和全微调）。特别是，作者观察到MoIL在大模型上相对于这些基线具有明显的优势。如表3所示，MoIL在大型语言模型上表现优于QKV-Tuning，例如在LLaMA-7B的ScienceQA任务上提高了+0.74%。在表4中，作者观察到在视觉-语言指令微调后，全微调和QKV-Tuning会显著损害NLP能力。相比之下，MoIL可以在保持NLP能力的同时提高多模态性能。从表9和10中，作者发现MoIL的训练成本远低于全微调，且接近QKV-Tuning。然而，与这些微调基线相比，MoIL的参数效率明显更高，例如在LLaMA-7B上，MoIL的参数为64.3M，而QKV-Tuning为1.6B。总体而言，这些结果进一步确认了MoIL的性能、泛化能力和参数效率。

4.4.3 消融研究

为了深入了解MoIL，作者在VQA和ITM上进行了广泛的实验，结果如表5和6所示。

累积消融：在表5中，作者首先验证了MoIL中每个设计的有效性。从表中可以看出，动量模仿学习方案和混合近似函数都提供了明显的性能提升，例如动量模仿学习方案在VQA上提高了+0.7%。与混合近似函数相比，模仿学习方案的性能提升更为显著，表明它可以更好地解决优化难题。同时，作者还观察到，在没有动量更新策略的情况下，模仿学习在VQA上的表现较差，即下降了-0.6%。通过结合所有设计，ViLT的性能可以显著提升，例如在VQA上提高了+1.2%。这些结果很好地确认了MoIL的每个设计。

维度大小的影响：在表6中，作者进一步验证了MoIL中不同维度设置的影响。从表中可以看出，MoIL的维度大小会显著影响微调性能。较小的维度通常会导致较大的误差$ϵ$。在实践中，MoIL在维度为96时几乎可以在所有下游任务上达到全微调的性能。同时，作者还发现不同任务对维度大小有不同的要求。对于ITM任务，维度为32时已经可以实现与全微调相当的性能，而对于VQA任务，则需要进一步增加到96。这意味着与预训练目标差距较大的下游任务通常需要更多的适应参数，这与作者的假设一致。

插入位置的影响：在表6的第二列中，作者还研究了MoIL在MSA中的插入位置。从表中可以看出，仅将MoIL部署到查询（Q）时，在ITM任务上已经可以实现与全微调相当的性能，即64.4%的IR@1，但其在VQA上的性能仍然较差。进一步将MoIL部署到值（V）后，VQA的性能从69.7提升到70.6。同时，“Q+K+V”的设置在VQA和ITM任务上均实现了最佳性能。

4.4.4 效率分析

在表9-10和图5-6中，作者比较了MoIL和现有方法的优化和推理效率。

训练效率：在表10中，作者比较了MoIL和现有方法的训练成本。特别是，MoIL的实际支出远低于全微调。原因在于，在模仿学习过程中，MoIL仅根据实现更新模型的一小部分，例如MSA中的Q、K、V投影。因此，即使与QKV-Tuning相比，其训练成本也没有显著增加，例如每次迭代增加+0.06秒。此外，作者还观察到MoIL比一些参数高效的方法（如Prompt tuning）更高效。例如，与Prompt tuning相比，MoIL可以节省高达82.6%的GPU内存和75.1%的训练时间。此外，MoIL的训练成本也与LoRA和Adapter相当。特别是，MoIL每次迭代的训练时间为1.41秒，与LoRA和Adapter的1.38秒非常接近。MoIL、LoRA和Adapter的内存占用也相似，即在ViLT上批量大小为64时约为9~10 GB。

图5展示了MoIL、LoRA和直接微调在VQA上的训练曲线。直接微调模型（即QKV-Tuning）是VL适应的最有效方法，但其缺点也很明显，即存储成本高。作者还看到，LoRA的优化效率始终低于MoIL和QKV-Tuning。尽管LoRA和MoIL的训练轮数相似，但MoIL可以显著提高VL任务的性能上限，已经接近QKV-Tuning。在图6中，作者比较了LoRA和MoIL在不同Transformer层上的近似误差。作者发现，MoIL可以显著减少近似误差，特别是在中间的Transformer层上，近似误差较大，表明这些层的权重在下游任务中变化更显著。总体而言，这些结果进一步确认了MoIL的训练效率。

推理效率：在表9中，作者比较了Prompt tuning、Adapter和LoRA的推理成本。表9的第一个观察结果是，Prompt tuning和Adapter在推理过程中会引入额外成本。特别是，Prompt tuning容易减慢大批量推理的速度，而Adapter会降低小批量推理的速度。相比之下，MoIL将适应模块重新参数化到VLP模型中，在推理过程中不会引入额外成本。这些结果很好地确认了MoIL的效率。

4.4.5 定性分析

为了进一步了解MoIL，作者可视化了其注意力图，并与LoRA和全微调进行了比较，结果如图7所示。从图中可以看出，全微调和MoIL都可以关注到正确的视觉区域。同时，MoIL的注意力与全微调非常接近，例如Exp-1和Exp-5，表明MoIL可以帮助模型在下游任务上有效学习注意力模式。与MoIL和全微调相比，LoRA的注意力更为分散，例如Exp-1和Exp-3。在某些示例中，它无法聚焦于正确的视觉区域，例如Exp-2和Exp-5。这些可视化结果也验证了MoIL的有效性。

5 结论

在本文中，作者专注于视觉-语言预训练（VLP）模型的参数高效迁移学习（PETL），并提出了一种新的PETL方法，称为MoIL。MoIL遵循低秩适应的原则，旨在通过动量模仿学习直接优化低秩适应的近似误差。同时，作者还提出了一种新的混合近似函数，以进一步降低学习难度。通过这些设计，MoIL显著提高了VLP模型的优化效率。为了验证MoIL，作者将其应用于一系列VLP模型，并在六个VL任务的八个基准数据集上进行了广泛的实验。实验结果表明，MoIL不仅在三个VLP模型上优于现有的PETL方法，还在推理过程中展示了卓越的效率。

声明

本文内容为论文学习收获分享，受限于知识能力，本文对原文的理解可能存在偏差，最终内容以原论文为准。本文信息旨在传播和学术交流，其内容由作者负责，不代表本号观点。文中作品文字、图片等如涉及内容、版权和其他问题，请及时与我们联系，我们将在第一时间回复并处理。