假设有一组有m个样本的集合 ,由未知的真实数据分布
生成。而我们的模型可以表述为
,
为我们模型的参数。
估计真实的概率分布
。
1. 最大似然估计
最大似然估计(Maximum Likelihood Estimation,MLE),又叫极大似然估计,是统计学中应用最广泛的一种未知参数估计方法。 它可以在已知随机变量属于哪种概率分布的前提下, 利用随机变量的一些观测值估计出分布的一些参数值。 所谓观测值,就是随机变量的采样值,也就是这个随机变量试验的真实结果值, 因为是我们能”看到”的值,所以称为观测值。
似然函数是一种关于统计模型中的参数的函数,表示模型参数的似然性。似然函数是给定联合样本值 x 下关于(未知)参数 θ 的函数:
使模型预测的分布可以和数据真实分布一致,就是要确定当前模型参数
使模型可以解释真实分布样本集
,问题转换成了一个已知样本集估计参数
的问题,参数
的最大似然估计为:
为了便于计算进行对数化,
对上述公式我们可以除以 m 求平均,m趋于无穷大时,此时该式子变为将数据经验分布 作为概率密度,求
的期望,并最大化。
,通过负对数似然就可以将这个问题转化为最小化问题。
当对数似然函数取得了最大值,我们认为预测模型趋近于真实模型,预测分布趋近于真实分布。
2. KL散度估计
最大似然的另一种观点为最小化训练集上的经验分布和模型分布之间的差异,这个差异我们通常使用KL散度进行描述:
为数据的经验分布,和模型无关,所以要最小化散度,我们只需要最小化:
显然最小化KL散度就是在最小化分布之间的交叉摘。(KL散度 - 目标分布熵 = 交叉熵)
所以给定样本集,用最大似然和最小化KL散度优化模型参数是等价的(都要假设模型输出的分
布,用样本集计算或代替真实分布)。
3. MSE
针对Z=X-Y,
,如果两随机变量独立则有:
假设预测分布和真实分布相互独立,且给定真实值分布条件下,模型预测值与真实值之间的误差服从标准高斯分布, ,
令,
已知真实分布样本时,求得了预测模型应该的目标分布。
将预测出的样本视为参数估计中采集的真实样本,添加最大似然约束,“让最优预测模型接近预测模型”,即让预测模型达到理论上能做到的最优预测模型,从而预测真实分布。最大化似然函数,
该式子的对比均方误差,两者显然等价,最小化均方差和最大化似然函数会得到相同的最优参数
。从概率的角度来说MSE是基于预测分布和真实分布相互独立,且给定真实值分布条件下,模型预测值与真实值之间的误差服从标准高斯分布假设的最大似然。
4. MASTERING ATARI WITH DISCRETE WORLD MODELS论文
4.1 Gaussian Likelihood
用高斯模型生成数据,就是假设模型输出的数据分布 为高斯分布,
应用最大似然估计,,使模型输出的数据分布接近真实分布。
论文中Gaussian Likelihood定义的image log loss和如下,

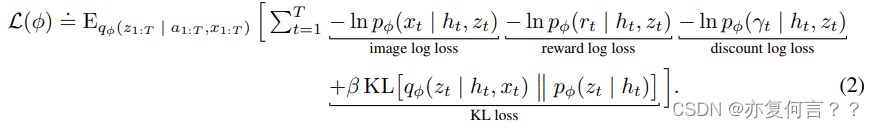
class LossModel(nn.Module):
def __init__(self, nx=1/64/64/3, nr=1, ng=1, nt=0.08, nq=0.1):
super(LossModel, self).__init__()
self.nx = nx
self.nr = nr
self.ng = ng
self.nt = nt
self.nq = nq
def forward(self, x, r, gamma, z_logits, z_sample, x_hat, r_hat, gamma_hat, z_hat_logits):
x_dist = torch.distributions.normal.Normal(
loc=x_hat,
scale=1.0
)
r_dist = torch.distributions.normal.Normal(
loc=r_hat,
scale=1.0
)
gamma_dist = torch.distributions.bernoulli.Bernoulli(
logits=gamma_hat
)
z_hat_dist = torch.distributions.one_hot_categorical.OneHotCategorical(
logits=z_hat_logits.reshape(-1, 32, 32)
)
z_dist = torch.distributions.one_hot_categorical.OneHotCategorical(
logits=z_logits.reshape(-1, 32, 32).detach()
)
z_sample = z_sample.reshape(-1, 32, 32)
loss = -self.nx*x_dist.log_prob(x).mean()\ # 计算x在正态分布中对应的概率的对数
-self.nr*r_dist.log_prob(r).mean()\
-self.ng*gamma_dist.log_prob(gamma.round()).mean()\
-self.nt*z_hat_dist.log_prob(z_sample.detach()).mean()\
+self.nq*z_dist.log_prob(z_sample).mean()
return loss根据公布的源码,image log loss计算步骤是:
1. 图像预测器输出具有单位方差的对角高斯似然的均值,即的高维均值,方差为1,这样可以构成重构image数据的分布
。
2. 将作为损失函数,计算梯度更新image predictor,更新image predictor网络的参数,更新网络的输出(即image predictor高斯模型的均值参数),从而使高斯模型输出分布
向着真实分布逼近。
4.2 类别分布隐变量的KL散度
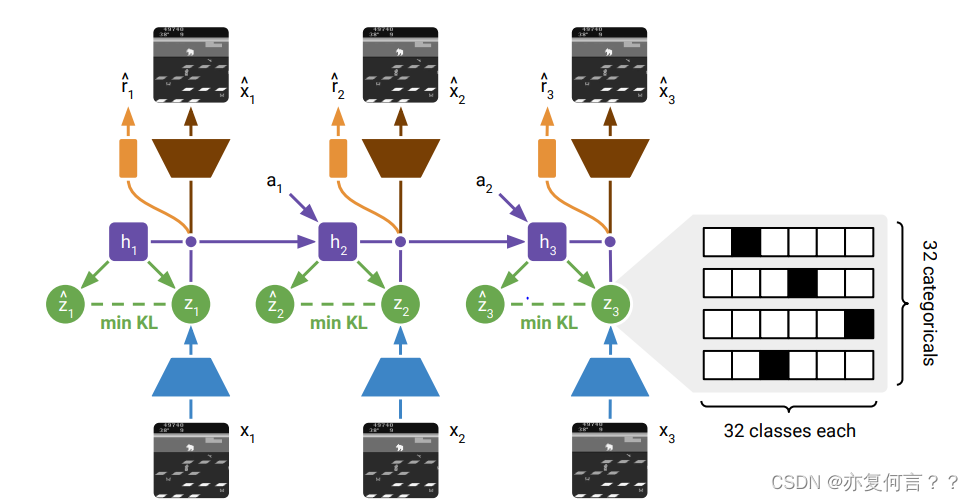
为使 分布和
分布接近,使用 KL 散度作为损失。在计算
和
的 KL 散度时,首先需要将它们的概率分布转换为概率密度函数。在代码中,使用了
torch.distributions.one_hot_categorical.OneHotCategorical 来表示这些离散分布,然后通过 sample() 方法获得了样本,再利用 torch.softmax 转换为概率分布。
在计算 KL 散度时,需要对概率分布取对数。然后,对于每个类别的概率,计算其与 $z$ 和 $z_{\text{hat}}$ 分布的比值,并乘以 $z$ 分布的概率。最后对所有类别进行求和,得到 KL 散度的值。
具体来说,对于 和
,它们的 KL 散度计算步骤如下:
- self.representation_model_mlp和self.transition_predictor网络分别输出
和
的event log probabilities (unnormalized),z_logits和z_hat_logits。
- 将
和
的 logits 利用
torch.distributions.one_hot_categorical.OneHotCategorical转换为概率分布,z_dist和z_hat_dist。 - 计算 KL 散度时,
,分成两部分似然进行计算,使用
分布采样出样本z_sample,当成似然函数的样本代入分布计算。
- 为了保持采样z_sample时梯度的连续性,需要使用 straight-through estimator 的技巧,即
z_sample = torch.distributions.one_hot_categorical.OneHotCategorical( logits=z_logits.reshape(-1, 32, 32)).sample() z_probs = torch.softmax(z_logits.reshape(-1, 32, 32), dim=-1) z_sample = z_sample + z_probs - z_probs.detach() 通过将
通过将 的采样样本和概率相加,然后减去概率的 detach 值来实现。
- 计算 KL 散度。在代码中,KL 散度的计算实际上是计算了两个分布之间的交叉熵(cross entropy),再加上一些系数项,因为 KL 散度可以被定义为两个分布之间的交叉熵减去一个熵项。(代码简化了原文中的kl balancing,直接使用了 log likelihood代替了)
KL_loss = -self.nt*z_hat_dist.log_prob(z_sample.detach()).mean()\ +self.nq*z_dist.log_prob(z_sample).mean()
4.3 一些思考
1. 为什么用高斯似然损失,不用KL散度,也不用MSE描述image和重构的image损失?
(1)KL散度与似然函数等价,因为world model将image predictor建模为高斯分布,没有网络将原始image样本解码高斯分布的参数,所以没法计算KL散度;
(2)将image predictor建模为高斯分布后,如果直接用image和重构image的MSE,则相当于没有用到这个假设。
2. 为什么类别隐变量之间用KL散度,不用类别隐变量之间直接做MSE?
因为直接用MSE的话,没有用到类别分布的假设。
3. 当模型输出建模为类别分布时,最大化类别似然函数是否等价于最小化交叉熵损失?
最大化似然等价于最小化KL散度,即,网络的输出为类别分布的概率参数,以此构造类别分布,再结合真实样本标签计算似然函数
x_dist = torch.distributions.one_hot_categorical.OneHotCategorical(
logits=x_logits.detach()
)
loss = -x_dist.log_prob(x).mean()只计算对应标签处的log probability,和cross entropy计算是等价的。
理论推导:
当是one-hot编码时,
,K为类别数
与交叉熵一致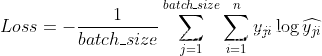
Reference






















 429
429











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








