机器学习课程期末综合测评

最新推荐文章于 2024-01-25 17:09:56 发布
最新推荐文章于 2024-01-25 17:09:56 发布
阅读量1.1k 收藏 16
点赞数 1
分类专栏： 机器学习 文章标签： 机器学习 人工智能 回归
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_42818403/article/details/122320059
版权

机器学习课程期末综合测评

文章目录


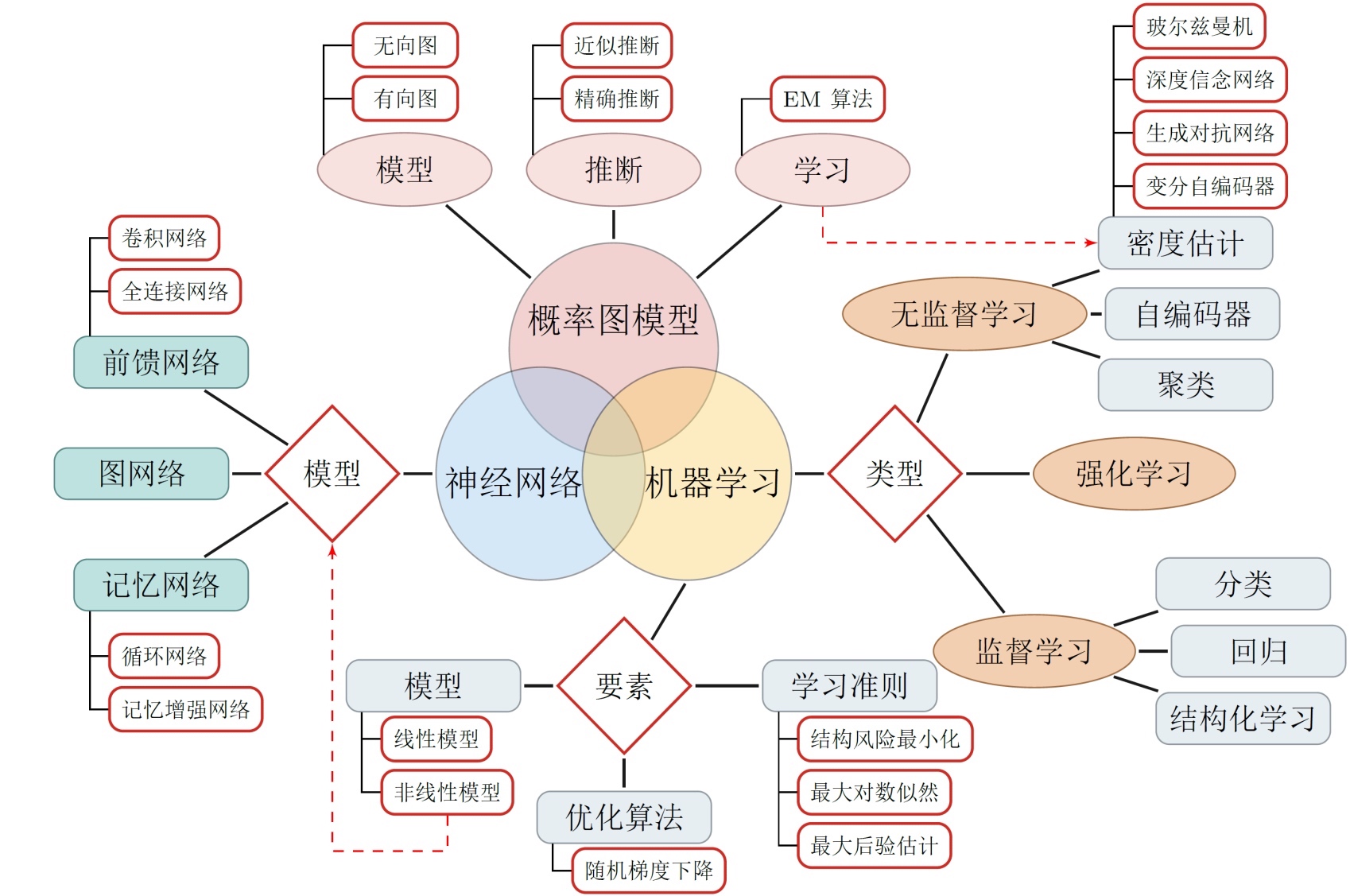
问题一: 机器学习的基本流程

要求: 结合线性回归在机器学习中的应用及原理,阐述从样本数据到应用预测的数学基本思想方法,并以视图的形式展示机器学习的基本流程,加以文字描述.

机器学习概览(基本流程)


机器学习的三要素

模型

  • 线性方法: f ( x , θ ) = w T x + b f(\mathbf{x}, \theta)=\mathbf{w}^{\mathrm{T}} \mathbf{x}+b f(x,θ)=wTx+b
  • 广义线性方法: f ( x , θ ) = w T ϕ ( x ) + b f(\mathbf{x}, \theta)=\mathbf{w}^{\mathrm{T}} \boldsymbol{\phi}(\mathbf{x})+b f(x,θ)=wTϕ(x)+b

如果 ϕ ( x ) \phi(x) ϕ(x) 为可学习的非线性基函数, f ( x , θ ) f(x, \theta) f(x,θ) 就等价于神经网络。

学习准则

  • 期望风险
    R ( f ) = E ( x , y ) ∼ p ( x , y ) [ L ( f ( x ) , y ) ] \mathcal{R}(f)=\mathbb{E}_{(\mathbf{x}, y) \sim p(\mathbf{x}, y)}[\mathcal{L}(f(\mathbf{x}), y)] R(f)=E(x,y)∼p(x,y)​[L(f(x),y)]
    优化
  • 梯度下降

常见的机器学习类型

线性模型

线性回归是解决回归类问题最常使用的算法模型，其算法思想和基本原理都是由多元统计分析发展而来，但在数据挖掘和机器学习领域中，也是不可多得的行之有效的算法模型。一方面，线性回归蕴藏的机器学习思想非常值得借鉴和学习，并且随着时间发展，在线性回归的基础上还诞生了许多功能强大的非线性模型。

可见，学习线性回归确实非常重要。

我们在进行机器学习算法学习过程中，仍然需要对线性回归这个统计分析算法进行系统深入的学习。但这里需要说明的是，线性回归的建模思想有很多理解的角度，此处我们并不需要从统计学的角度来理解、掌握和应用线性回归算法，很多时候，利用机器学习的思维来理解线性回归，会是一种更好的理解方法，这也将是我们这部分内容讲解线性回归的切入角度。

线性回归的机器学习表示方法

  • 核心逻辑

任何机器学习算法首先都有一个最底层的核心逻辑, 当我们在利用机器学习思维理解线性回归的时候, 首先也是要探究其底层逻辑。 值得庆辛的是, 虽然线性回归源于统计分析, 但其算法底层逻辑和机器学习算法高度契合。

在给定 n \mathrm{n} n 个属性描绘的客观事物 z = ( x 1 , x 2 , … , x n ) z=\left(x_{1}, x_{2}, \ldots, x_{n}\right) z=(x1​,x2​,…,xn​) 中, 每个都用于描绘某一次观测时事物在某个维度表现出来的数值属性值。当我 们在建立机器学习模型捕捉事物运行的客观规律时, 本质上是希望能够综合这些维度的属性值来描绘事物最终运行结果, 而最简单的 综合这些属性的方法就是对其进行加权求和汇总，这即是线性回归的方程式表达形式:
y ^ = w 0 + w 1 x i 1 + w 2 x i 2 + … + + w n x i n \hat{y}=w_{0}+w_{1} x_{i 1}+w_{2} x_{i 2}+\ldots++w_{n} x_{i n} y^​=w0​+w1​xi1​+w2​xi2​+…++wn​xin​

w w w被统称为模型的参数, 其中 w 0 w_{0} w0​被称为截距(intercept),$ w_{1} \sim w_{n} 被 称 为 回 归 系 数 ( r e g r e s s i o n c o e f f i f f i f f i c i e n t ) , 有 时 也 是 使 用 被称为回归系数(regression coeffiffifficient), 有时也是使用 被称为回归系数(regressioncoeffiffifficient),有时也是使用\beta 或 者 或者 或者\theta$来表示。这个表达式, 其实就和我们小学时就无比熟悉的 y = a x + b y=a x+b y=ax+b 是同样的性质。其中 x i 1 x_{i 1} xi1​ 是我们的目标变量, 也就是标签。是样本 i i i 上的特征不同特征。如果考虑我们有 m m m个样本, 则回归结果可以被写作:
y ^ = w 0 + w 1 x 1 + w 2 x 2 + … + + w n x n \hat{y}=w_{0}+w_{1} x_{1}+w_{2} x_{2}+\ldots++w_{n} x_{n} y^​=w0​+w1​x1​+w2​x2​+…++wn​xn​
其中 y y y 是包含了 m \mathrm{m} m 个全部的样本的回归结果的列向量 (结构为 ( m , 1 ) (\mathrm{m}, 1) (m,1), 由于只有一列, 以列的形式表示, 所以叫做列向量) 。注意, 我们 通常使用粗体的小写字母来表示列向量, 粗体的大写字母表示矩阵或者行列式。我们可以使用矩阵来表示这个方程, 其中可以被看做 是一个结构为 ( n + 1 , 1 ) (n+1,1) (n+1,1) 的列矩阵, 是一个结构为 ( m , n + 1 ) (m, n+1) (m,n+1) 的特征矩阵, 则有:
[ y ^ 1 y ^ 2 y ^ 3 … y ^ m ] = [ 1 x 11 x 12 x 13 … x 1 n 1 x 21 x 22 x 23 … x 2 n 1 x 31 x 32 x 33 … x 3 n … 1 x m 1 x m 2 x m 3 … x m n ] ∗ [ w ^ 1 w ^ 2 w ^ 3 … w ^ n ] \begin{gathered} {\left[\begin{array}{c} \hat{y}_{1} \\ \hat{y}_{2} \\ \hat{y}_{3} \\ \ldots \\ \hat{y}_{m} \end{array}\right]=\left[\begin{array}{cccccc} 1 & x_{11} & x_{12} & x_{13} & \ldots & x_{1 n} \\ 1 & x_{21} & x_{22} & x_{23} & \ldots & x_{2 n} \\ 1 & x_{31} & x_{32} & x_{33} & \ldots & x_{3 n} \\ \ldots & & & & & \\ 1 & x_{m 1} & x_{m 2} & x_{m 3} & \ldots & x_{m n} \end{array}\right] *\left[\begin{array}{c} \hat{w}_{1} \\ \hat{w}_{2} \\ \hat{w}_{3} \\ \ldots \\ \hat{w}_{n} \end{array}\right]} \\ \end{gathered} ⎣⎢⎢⎢⎢⎡​y^​1​y^​2​y^​3​…y^​m​​⎦⎥⎥⎥⎥⎤​=⎣⎢⎢⎢⎢⎡​111…1​x11​x21​x31​xm1​​x12​x22​x32​xm2​​x13​x23​x33​xm3​​…………​x1n​x2n​x3n​xmn​​⎦⎥⎥⎥⎥⎤​∗⎣⎢⎢⎢⎢⎡​w^1​w^2​w^3​…w^n​​⎦⎥⎥⎥⎥⎤​​
y ^ = X w \hat{y}=X w y^​=Xw

线性回归的任务, 就是构造一个预测函数来映射输入的特征矩阵和标签值的线性关系, 这个预测函数在不同的教材上写法不同, 可能写作 f ( x ) , y w ( x ) f(x), y_{w}(x) f(x),yw​(x), 或者 h ( x ) h(x) h(x) 等等形式, 但无论如何, 这个预测函数的本质就是我们需要构建的模型。

  • 优化目标

对于线性回归而言, 预测函数 y ^ = X w \hat{y}=X w y^​=Xw 就是我们的模型, 在机器学习我们也称作 “决策数”。其中只有 w w w 是末知的, 所以线性回归原理的核心就是找出模型的参数向量 w w w 。但我们怎样才能栘求解出参数向量呢? 我们需要依赖一个重要概念: 损失函数。

在之前的算法学习中，我们提到过两种模型表现：在训练集上的表现，和在测试集上的表现。我们建模，是追求模型在测试集上的表现最优，因此模型的评估指标往往是⽤来衡量模型在测试集上的表现的。然而，线性回归有着基于训练数据求解参数的需求，并且希望训练出来的模型能够尽可能地拟合训练数据，即模型在训练集上的预测准确率越靠近100%越好。

因此，我们使用损失函数这个评估指标，来衡量系数为 w w w 的模型拟合训练集时产生的信息损失的大小，并以此衡量参数 w w w 的优劣。如果用一组参数建模后，模型在训练集上表现良好，那我们就说模型拟合过程中的损失很小，损失函数的值很小，这一组参数就优秀；相反，如果模型在训练集上表现糟糕，损失函数就会很大，模型就训练不足，效果较差，这一组参数也就比较差。即是说，我们在求解参数 w w w 时，追求损失函数最小，让模型在训练数据上的拟合效果最优，即预测准确率尽量靠近100%。

（注意：对于非参数模型没有损失函数，比如KNN、决策树）

对于有监督学习算法而言，建模都是依据有标签的数据集，回归类问题则是对客观事物的⼀个定量判别。这里以 $ y_i$ 作为第 i i i 行数据的标签，且 y i y_i yi​ 为连续变量， x i x_i xi​ 为第 i i i 行特征值所组成的向量，则线性回归建模优化方向就是希望模型判别的 y ^ i \hat y_i y^​i​ 尽可能地接近实际的 y i y_i yi​ 。而对于连续型变量而言，邻近度度量方法可采用 S S E SSE SSE 来进行计算， S S E SSE SSE 称作「残差平方和」，也称作「误差平方和」或者「离差平方和」。

因此我们的优化目标可用下述方程来进行表示：

min ⁡ w ∑ i = 1 m ( y i − y ^ i ) 2 = min ⁡ w ∑ i = 1 m ( y i − X i w ) 2 \min _{w} \sum_{i=1}^{m}\left(y_{i}-\hat{y}_{i}\right)^{2}=\min _{w} \sum_{i=1}^{m}\left(y_{i}-X_{i} w\right)^{2} wmin​i=1∑m​(yi​−y^​i​)2=wmin​i=1∑m​(yi​−Xi​w)2
来看一个简单的小例子。假设现在 w w w 为 [ 1 , 2 ] [1,2] [1,2] 这样一个向量, 求解出的模型为 y = x 1 + 2 x 2 y=x_{1}+2 x_{2} y=x1​+2x2​ 。

样本特征 1特征 2真实标签
010.53
1-10.52

则我们的损失函数的值就是:
( 3 − ( 1 ∗ 1 + 2 ∗ 0.5 ) ) 2 + ( 2 − ( 1 ∗ ( − 1 ) + 2 ∗ 0.5 ) ) 2 ( y 1 − y ^ 1 ) 2 + ( y 2 − y ^ 2 ) 2 \begin{gathered} (3-(1 * 1+2 * 0.5))^{2}+(2-(1 *(-1)+2 * 0.5))^{2} \\ \left(y_{1}-\hat{y}_{1}\right)^{2}+\left(y_{2}-\hat{y}_{2}\right)^{2} \end{gathered} (3−(1∗1+2∗0.5))2+(2−(1∗(−1)+2∗0.5))2(y1​−y^​1​)2+(y2​−y^​2​)2​

  • 最小二乘法

现在问题转换成了求解 S S E SSE SSE 最小化的参数向量 w w w ，这种通过最小化真实值和预测值之间的 S S E SSE SSE 来求解参数的方法叫做最小二乘法。

下面我们来用代码尝试一下。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#生成横坐标   范围 0 -10
np.random.seed(420)
x = np.random.rand(50) * 10 #50个点
x

# y = 2x - 5
#添加扰动项
np.random.seed(420)
y = 2 * x - 5 + np.random.randn(50) #正太分布下的随机数

plt.plot(x,y,'o')

生成样本点

Figure_1

现在对上图数据进行拟合：

from sklearn.linear_model import LinearRegression

#实例化
lr = LinearRegression(fit_intercept=True)

x2 = x.reshape(-1,1)

# 训练模型
lr.fit(x2, y)

# 生成绘制直线的横坐标
xfit = np.linspace(0,10,100) #从0到10  生成100个

xfit2 = xfit.reshape(-1,1)

yfit = lr.predict(xfit2) #预测

#画出点的直线
plt.plot(xfit,yfit)
#画出原来训练集的点
plt.plot(x,y,'o')

拟合结果:

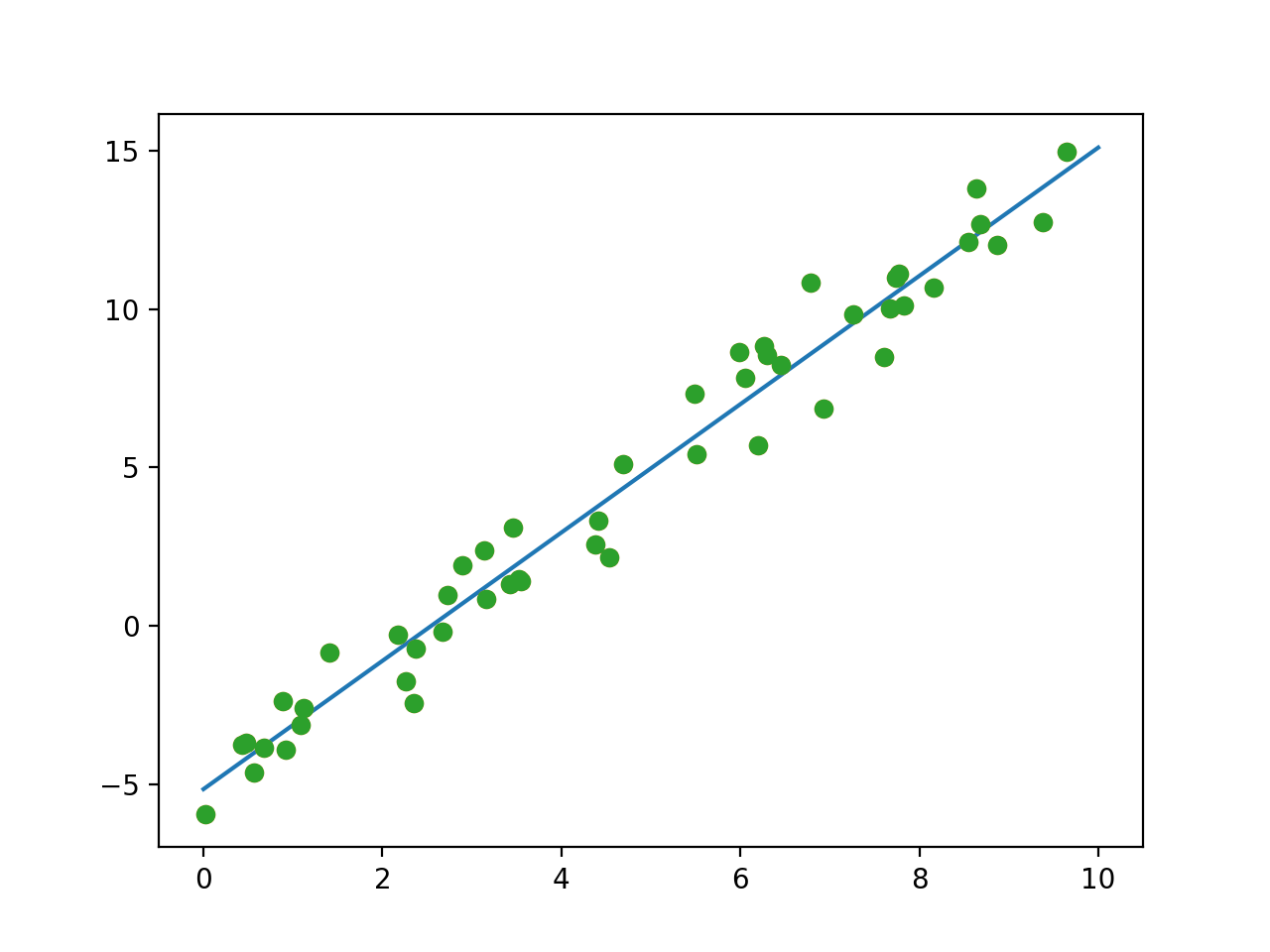
Figure_1

看上去效果还是不错的。
假设该拟合直线为 y ^ = w 0 + w 1 x \hat{y}=w_{0}+w_{1} x y^​=w0​+w1​x 。现在我们的目标是使得该拟合直线的总的残差和达到最小, 也就是最小化 S S E S S E SSE 。 我们令该直线是以均值为核心的「均值回归 ┘ \lrcorner ┘, 即散点的 x ˉ \bar{x} xˉ 和 y ˉ \bar{y} yˉ​ 必经过这条直线:
y ˉ = w 0 + w 1 x ˉ \bar{y}=w_{0}+w_{1} \bar{x} yˉ​=w0​+w1​xˉ
对于真实值y来说, 我们可以得到:
y = w 0 + w 1 x + ϵ y=w_{0}+w_{1} x+\epsilon y=w0​+w1​x+ϵ
这里的 ϵ \epsilon ϵ 即为 「 「 「 残差 ┘ \lrcorner ┘, 对其进行变形, 则残差平方和 S S E S S E SSE 就为:
∑ ϵ 2 = ∑ ( y − w 0 − w 1 x ) 2 \sum \epsilon^{2}=\sum\left(y-w_{0}-w_{1} x\right)^{2} ∑ϵ2=∑(y−w0​−w1​x)2
要求得残差平方和最小值, 我们通过微积分求偏导算其极值来解决。这里我们计算残差最小对应的参数 w 1 w_{1} w1​ :

∂ ∂ w 1 = 2 ∑ ( y − w 0 − w 1 x ) ( − x ) = 0  一阶导数  ∵ w 0 = y ˉ − w 1 x ˉ ∴ ∑ ( y − y ˉ + w 1 x ˉ − w 1 x ) ( x ) = 0 ∑ ( y x − y ˉ x + w 1 x ˉ x − w 1 x 2 ) = 0 ∑ ( y x − y ˉ x ) + ∑ ( w 1 x ˉ x − w 1 x 2 ) = 0 ∑ ( y x − y ˉ x ) = ∑ ( w 1 x 2 − w 1 x ˉ x ) ∑ ( y − y ˉ ) x = w 1 ∑ ( x − x ˉ ) x ∑ w 1 = ∑ ( y − y ˉ ) x ∑ ( x − x ˉ ) x \begin{aligned} \frac{\partial}{\partial w_{1}} &=2 \sum\left(y-w_{0}-w_{1} x\right)(-x)=0 \quad \text { 一阶导数 } \\ & \because w_{0}=\bar{y}-w_{1} \bar{x} \\ & \therefore \sum\left(y-\bar{y}+w_{1} \bar{x}-w_{1} x\right)(x)=0 \\ & \sum\left(y x-\bar{y} x+w_{1} \bar{x} x-w_{1} x^{2}\right)=0 \\ & \sum(y x-\bar{y} x)+\sum\left(w_{1} \bar{x} x-w_{1} x^{2}\right)=0 \\ & \sum(y x-\bar{y} x)=\sum\left(w_{1} x^{2}-w_{1} \bar{x} x\right) \\ & \sum(y-\bar{y}) x=w_{1} \sum(x-\bar{x}) x \\ & \sum w_{1}=\frac{\sum(y-\bar{y}) x}{\sum(x-\bar{x}) x} \end{aligned} ∂w1​∂​​=2∑(y−w0​−w1​x)(−x)=0 一阶导数 ∵w0​=yˉ​−w1​xˉ∴∑(y−yˉ​+w1​xˉ−w1​x)(x)=0∑(yx−yˉ​x+w1​xˉx−w1​x2)=0∑(yx−yˉ​x)+∑(w1​xˉx−w1​x2)=0∑(yx−yˉ​x)=∑(w1​x2−w1​xˉx)∑(y−yˉ​)x=w1​∑(x−xˉ)x∑w1​=∑(x−xˉ)x∑(y−yˉ​)x​​
根䝻协方差和方差的猚㝵公式，我们将分子分母同时除以 n − 1 n-1 n−1, 则可以得到：
w ^ 1 = ∑ ( y − y ˉ ) ( x − x ˉ ) ∑ ( x − x ˉ ) 2 \hat{w}_{1}=\frac{\sum(y-\bar{y})(x-\bar{x})}{\sum(x-\bar{x})^{2}} w^1​=∑(x−xˉ)2∑(y−yˉ​)(x−xˉ)​
同理，可知：
w ^ 0 = y ˉ − w ^ 1 x ˉ \hat{w}_{0}=\bar{y}-\hat{w}_{1} \bar{x} w^0​=yˉ​−w^1​xˉ

此时, 使得 S S E S S E SSE 最小的量 w ^ 0 , w ^ 1 \hat{w}_{0}, \hat{w}_{1} w^0​,w^1​ 称为总体参数 w 0 , w 1 w_{0}, w_{1} w0​,w1​ 的最小二乘估计值, 预测方程 y ^ = w ^ 0 + w ^ 1 x \hat{y}=\hat{w}_{0}+\hat{w}_{1} x y^​=w^0​+w^1​x 称为最小二乘直线。

问题二: 决策树

要求: 利用决策树应用划分

  1. 在构建决策树过程中有哪些优化方法

  2. 举例说明信息增益原理及其改进途径

  3. 试用类C语言(或Python)写出剪枝算法.

决策树是一种自上而下，对样本数据进行树形分类的过程，由结点和有向边 组成.结点分为内部结点和叶结点，其中每个内部结点表示一个特征或属性，叶 结点表示类别.从顶部根结点开始，所有样本聚在一起.经过根结点的划分，样 本被分到不同的子结点中.再根据子结点的特征进一步划分，直至所有样本都被 归到某一个类别（即叶结点）中.

决策树作为最基础、最常见的有监督学习模型，常被用于分类问题和回归问 题，在市场营销和生物医药等领域尤其受欢迎，主要因为树形结构与销售、诊断 等场景下的决策过程十分相似.将决策树应用集成学习的思想可以得到随机森 林、梯度提升决策树等模型，这些将在第12章中详细介绍.完全生长的决策树模 型具有简单直观、解释性强的特点，值得读者认真理解，这也是为融会贯通集成 学习相关内容所做的铺垫.

一般而言，决策树的生成包含了特征选择、树的构造、树的剪枝三个过程， 本节将在第一个问题中对几种常用的决策树进行对比，在第二个问题中探讨决策 树不同剪枝方法之间的区别与联系.

问题1 在构建决策树过程中有哪些优化方法

我们知道，决策树的目标是从一组样本数据中，根据不同的特征和属性，建 立一棵树形的分类结构.我们既希望它能拟合训练数据，达到良好的分类效果， 同时又希望控制其复杂度，使得模型具有一定的泛化能力.对于一个特定的问 题，决策树的选择可能有很多种.

从若干不同的决策树中选取最优的决策树是一个NP完全问题，在实际中我们 通常会采用启发式学习的方法去构建一棵满足启发式条件的决策树.

常用的决策树算法有ID3、C4.5、CART，它们构建树所使用的启发式函数各 是什么？除了构建准则之外，它们之间的区别与联系是什么？

分析与解答

首先，我们回顾一下这几种决策树构造时使用的准则.

■ ID3—— 最大信息增益

对于样本集合 D D D, 类别数为 K K K, 数据集 D D D 的经验熵表示为
H ( D ) = − ∑ k = 1 K ∣ C k ∣ ∣ D ∣ log ⁡ 2 ∣ C k ∣ ∣ D ∣ H(D)=-\sum_{k=1}^{K} \frac{\left|C_{k}\right|}{|D|} \log _{2} \frac{\left|C_{k}\right|}{|D|} H(D)=−k=1∑K​∣D∣∣Ck​∣​log2​∣D∣∣Ck​∣​

其中 C k C_{k} Ck​ 是样本集合 D D D 中属于第 k k k 类的样本子集, ∣ C k ∣ \mid C_{k}\mid ∣Ck​∣ 表示该子集的元素个数, ∣ D ∣ \mid D \mid ∣D∣ 表示 样本集合的元素个数.

然后计算某个特征 A A A 对于数据集 D D D 的经验条件樀 H ( D ∣ A ) H(D \mid A) H(D∣A) 为
H ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ( − ∑ k = 1 k ∣ ∣ D i k ∣ ∣ D i ∣ log ⁡ 2 ∣ D i k ∣ ∣ D i ∣ ) , H(D \mid A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|}\left(-\sum_{k=1}^{k} \mid \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \log _{2} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|}\right), H(D∣A)=i=1∑n​∣D∣∣Di​∣​H(Di​)=i=1∑n​∣D∣∣Di​∣​(−k=1∑k​∣∣Di​∣∣Dik​∣​log2​∣Di​∣∣Dik​∣​),
其中, D i D_{i} Di​ 表示 D D D 中特征 A A A 取第 i i i 个值的样本子集, D i k D_{i k} Dik​ 表示 D i D_{i} Di​ 中属于第 k k k 类的样本子集.

于是信息增益 g ( D , A ) g(D, A) g(D,A) 可以表示为二者之差, 可得
g ( D , A ) = H ( D ) − H ( D ∣ A ) . g(D, A)=H(D)-H(D \mid A) . g(D,A)=H(D)−H(D∣A).

■ C4.5——最大信息增益比

特征 A A A 对于数据集 D D D 的信息增益比定义为
g R ( D , A ) = g ( D , A ) H A ( D ) , g_{R}(D, A)=\frac{g(D, A)}{H_{A}(D)}, gR​(D,A)=HA​(D)g(D,A)​,
其中
H A ( D ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ log ⁡ 2 ∣ D i ∣ ∣ D ∣ H_{A}(D)=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \log _{2} \frac{\left|D_{i}\right|}{|D|} HA​(D)=−i=1∑n​∣D∣∣Di​∣​log2​∣D∣∣Di​∣​

称为数据集 D D D 关于 A A A 的取值熵.

■ CART——最大基尼指数（Gini）

Gini描述的是数据的纯度, 与信息熵含义类似.
Gini ⁡ ( D ) = 1 − ∑ k = 1 n ( ∣ C k ∣ ∣ D ∣ ) 2 . \operatorname{Gini}(D)=1-\sum_{k=1}^{n}\left(\frac{\left|C_{k}\right|}{|D|}\right)^{2} . Gini(D)=1−k=1∑n​(∣D∣∣Ck​∣​)2.
CART在每一次迭代中选择基尼指数最小的特征及其对应的切分点进行分类. 但与ID3、C4.5不同的是, CART是一颗二叉树, 采用二元切割法, 每一步将数据 按特征 A A A 的取值切成两份, 分别进入左右子树.特征 A A A 的 Gini指数定义为
Gini ⁡ ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ Gini ⁡ ( D i ) .  \operatorname{Gini}(D \mid A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \operatorname{Gini}\left(D_{i}\right) \text {. } Gini(D∣A)=i=1∑n​∣D∣∣Di​∣​Gini(Di​). 

问题2 举例说明信息增益原理及其改进途径

上面这些定义听起来有点像绕口令，不妨我们用一个例子来简单说明下信息增益原理计算过程.假设共有5个人追求场景中的女孩，年龄有两个属性（老，年轻），长相有三个属性（帅，一般，丑），工资有三个属性（高，中等，低），会写代码有两个属性（会，不会），最终分类结果有两类（见，不见）.我们根据女孩有监督的主观意愿可以得到下表.

年龄长相工资写代码类别
小A老帅高不会不见
小B年轻一般中等会见
小C年轻丑高不会不见
小D年轻一般高会见
小L年轻一般低不会不见

在这个问题中,
H ( D ) = − 3 5 log ⁡ 2 3 5 − 2 5 log ⁡ 2 2 5 = 0.971 H(D)=-\frac{3}{5} \log _{2} \frac{3}{5}-\frac{2}{5} \log _{2} \frac{2}{5}=0.971 H(D)=−53​log2​53​−52​log2​52​=0.971

根据式
H ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ( − ∑ k = 1 k ∣ ∣ D i k ∣ ∣ D i ∣ log ⁡ 2 ∣ D i k ∣ ∣ D i ∣ ) , H(D \mid A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|}\left(-\sum_{k=1}^{k} \mid \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \log _{2} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|}\right), H(D∣A)=i=1∑n​∣D∣∣Di​∣​H(Di​)=i=1∑n​∣D∣∣Di​∣​(−k=1∑k​∣∣Di​∣∣Dik​∣​log2​∣Di​∣∣Dik​∣​),
可计算出4个分支结点的信息熵为
H ( D ∣  年龄  ) = 1 5 H (  老  ) + 4 5 H (  年轻  ) = 1 5 ( − 0 ) + 4 5 ( − 2 4 log ⁡ 2 2 4 − 2 4 log ⁡ 2 2 4 ) = 0.8 , H ( D ∣  长相  ) = 1 5 H (  帅  ) + 3 5 H ( −  般  ) + 1 5 H (  丑  ) = 0 + 3 5 ( − 2 3 log ⁡ 2 2 3 − 1 3 log ⁡ 2 1 3 ) + 0 = 0.551 , H ( D ∣  工资  ) = 3 5 H (  高  ) + 1 5 H (  中等  ) + 1 5 H (  低  ) = 3 5 ( − 2 3 log ⁡ 2 2 3 − 1 3 log ⁡ 2 1 3 ) + 0 + 0 = 0.551 , H ( D ∣  写代码  ) = 3 5 H (  不会  ) + 2 5 H (  会  ) = 3 5 ( 0 ) + 2 5 ( 0 ) = 0 \begin{aligned} H(D \mid \text { 年龄 }) &=\frac{1}{5} H(\text { 老 })+\frac{4}{5} H(\text { 年轻 }) \\ &=\frac{1}{5}(-0)+\frac{4}{5}\left(-\frac{2}{4} \log _{2} \frac{2}{4}-\frac{2}{4} \log _{2} \frac{2}{4}\right)=0.8, \\ H(D \mid \text { 长相 }) &=\frac{1}{5} H(\text { 帅 })+\frac{3}{5} H(-\text { 般 })+\frac{1}{5} H(\text { 丑 }) \\ &=0+\frac{3}{5}\left(-\frac{2}{3} \log _{2} \frac{2}{3}-\frac{1}{3} \log _{2} \frac{1}{3}\right)+0=0.551, \\ H(D \mid \text { 工资 }) &=\frac{3}{5} H(\text { 高 })+\frac{1}{5} H(\text { 中等 })+\frac{1}{5} H(\text { 低 }) \\ &=\frac{3}{5}\left(-\frac{2}{3} \log _{2} \frac{2}{3}-\frac{1}{3} \log _{2} \frac{1}{3}\right)+0+0=0.551, \\ H(D \mid \text { 写代码 })=\frac{3}{5} H(\text { 不会 })+\frac{2}{5} H(\text { 会 }) \\ =\frac{3}{5}(0)+\frac{2}{5}(0)=0 \end{aligned} H(D∣ 年龄 )H(D∣ 长相 )H(D∣ 工资 )H(D∣ 写代码 )=53​H( 不会 )+52​H( 会 )=53​(0)+52​(0)=0​=51​H( 老 )+54​H( 年轻 )=51​(−0)+54​(−42​log2​42​−42​log2​42​)=0.8,=51​H( 帅 )+53​H(− 般 )+51​H( 丑 )=0+53​(−32​log2​32​−31​log2​31​)+0=0.551,=53​H( 高 )+51​H( 中等 )+51​H( 低 )=53​(−32​log2​32​−31​log2​31​)+0+0=0.551,​
于是, 根据式
g ( D , A ) = H ( D ) − H ( D ∣ A ) . g(D, A)=H(D)-H(D \mid A) . g(D,A)=H(D)−H(D∣A).
可计算出各个特征的信息增益为
g ( D , 年龄  ) = 0.171 , g ( D , 长相  ) = 0.42 , g ( D ,工资  ) = 0.42 , g ( D , 写代码  ) = 0.971. \begin{gathered} g(D \text {, 年龄 })=0.171, g(D \text {, 长相 })=0.42, \\ g(D \text {,工资 })=0.42, g(D \text {, 写代码 })=0.971 . \end{gathered} g(D, 年龄 )=0.171,g(D, 长相 )=0.42,g(D,工资 )=0.42,g(D, 写代码 )=0.971.​
显然, 特征“写代码”的信息增益最大, 所有的样本根据此特征, 可以直接被分到叶结点（即见或不见）中, 完成决策树生长.当然, 在实际应用中, 决策树往往不能通过一个特征就完成构建, 需要在经验熵非 0 的类别中继续生长.

通过对比三种决策树的构造准则，以及在同一例子上的不同表现，我们不难 总结三者之间的差异.

首先，ID3是采用信息增益作为评价标准，除了“会写代码”这一逆天特征外， 会倾向于取值较多的特征.因为，信息增益反映的是给定条件以后不确定性减少 的程度，特征取值越多就意味着确定性更高，也就是条件熵越小，信息增益越 大.这在实际应用中是一个缺陷.比如，我们引入特征“DNA”，每个人的DNA都 不同，如果ID3按照“DNA”特征进行划分一定是最优的（条件熵为0），但这种分 类的泛化能力是非常弱的.因此，C4.5实际上是对ID3进行优化，通过引入信息增 益比，一定程度上对取值比较多的特征进行惩罚，避免ID3出现过拟合的特性，提 升决策树的泛化能力.

其次，从样本类型的角度，ID3只能处理离散型变量，而C4.5和CART都可以 处理连续型变量.C4.5处理连续型变量时，通过对数据排序之后找到类别不同的 分割线作为切分点，根据切分点把连续属性转换为布尔型，从而将连续型变量转 换多个取值区间的离散型变量.而对于CART，由于其构建时每次都会对特征进行 二值划分，因此可以很好地适用于连续性变量.

从应用角度，ID3和C4.5只能用于分类任务，而CART（Classification and Regression Tree，分类回归树）从名字就可以看出其不仅可以用于分类，也可以应 用于回归任务（回归树使用最小平方误差准则）.

此外，从实现细节、优化过程等角度，这三种决策树还有一些不同.比如， ID3对样本特征缺失值比较敏感，而C4.5和CART可以对缺失值进行不同方式的处 理；ID3和C4.5可以在每个结点上产生出多叉分支，且每个特征在层级之间不会复 用，而CART每个结点只会产生两个分支，因此最后会形成一颗二叉树，且每个特 征可以被重复使用；ID3和C4.5通过剪枝来权衡树的准确性与泛化能力，而CART 直接利用全部数据发现所有可能的树结构进行对比.

问题3 试用类C语言(或Python)写出剪枝算法.

一棵完全生长的决策树会面临一个很严重的问题，即过拟合.假设我们真的需要考虑DNA特征，由于每个人的DNA都不同，完全生长的决策树所对应的每个叶结点中只会包含一个样本，这就导致决策树是过拟合的.用它进行预测时，在测试集上的效果将会很差.因此我们需要对决策树进行剪枝，剪掉一些枝叶，提 升模型的泛化能力.

决策树的剪枝通常有两种方法，预剪枝（Pre-Pruning）和后剪枝（PostPruning）.那么这两种方法是如何进行的呢？它们又各有什么优缺点？

分析与解答

预剪枝，即在生成决策树的过程中提前停止树的增长.而后剪枝，是在已生成的过拟合决策树上进行剪枝，得到简化版的剪枝决策树.

■ 预剪枝

预剪枝的核心思想是在树中结点进行扩展之前，先计算当前的划分是否能带来模型泛化能力的提升，如果不能，则不再继续生长子树.此时可能存在不同类 别的样本同时存于结点中，按照多数投票的原则判断该结点所属类别.预剪枝对于何时停止决策树的生长有以下几种方法.

（1）当树到达一定深度的时候，停止树的生长.

（2）当到达当前结点的样本数量小于某个阈值的时候，停止树的生长.

（3）计算每次分裂对测试集的准确度提升，当小于某个阈值的时候，不再继 续扩展.

预剪枝具有思想直接、算法简单、效率高等特点，适合解决大规模问题.但如何准确地估计何时停止树的生长（即上述方法中的深度或阈值），针对不同问题会有很大差别，需要一定经验判断.且预剪枝存在一定局限性，有欠拟合的风险，虽然当前的划分会导致测试集准确率降低，但在之后的划分中，准确率可能 会有显著上升.

■ 后剪枝

后剪枝的核心思想是让算法生成一棵完全生长的决策树，然后从最底层向上计算是否剪枝.剪枝过程将子树删除，用一个叶子结点替代，该结点的类别同样按照多数投票的原则进行判断.同样地，后剪枝也可以通过在测试集上的准确率进行判断，如果剪枝过后准确率有所提升，则进行剪枝.相比于预剪枝，后剪枝方法通常可以得到泛化能力更强的决策树，但时间开销会更大.

常见的后剪枝方法包括错误率降低剪枝（Reduced Error Pruning，REP）、悲观剪枝（Pessimistic Error Pruning，PEP）、代价复杂度剪枝（Cost Complexity Pruning，CCP）、最小误差剪枝（Minimum Error Pruning，MEP）、CVP（Critical Value Pruning）、OPP（Optimal Pruning）等方法.

下面通过决策树一回归举例

核心: 划分点选择 + 输出值确定.

一、概述

决策树是一种基本的分类与回归方法, 本文叙述的是回归部分.回归决策树主要指 CART (classification and regression tree)算法, 内部结点特征的取值为 “是”和“否”, 为二叉树 结构.

所谓回归, 就是根据特征向量来决定对应的输出值.回归树就是将特征空间划分成若干 单元, 每一个划分单元有一个特定的输出.因为每个结点都是“是”和“否”的判断, 所以划分 的边界是平行于坐标轴的.对于测试数据, 我们只要按照特征将其归到某个单元, 便得到对 应的输出值.

【例】左边为对二维平面划分的决策树, 右边为对应的划分示意图, 其中 c 1 , c 2 , c 3 , c 4 , c 5 c_{1}, c_{2}, c_{3}, c_{4}, c_{5} c1​,c2​,c3​,c4​,c5​ 是对应每个划分单元的输出.

截屏2021-11-23 下午12.44.37

比如现在对一个新的向量 ( 6 , 6 ) (6,6) (6,6) 决定它对应的输出.第一维分量 6 介于 5 和 8 之间, 第二 维分量 6 小于 8 , 根据此决策树很容易判断 ( 6 , 6 ) (6,6) (6,6) 所在的划分单元, 其对应的输出值为 c 3 c_{3} c3​.

划分的过程也就是建立树的过程, 每划分一次, 随即确定划分单元对应的输出, 也就多 了一个结点.当根据停止条件划分终止的时候, 最终每个单元的输出也就确定了, 也就是叶 结点.

二、回归树建立

既然要划分, 切分点怎么找? 输出值又怎么确定? 这两个问题也就是回归决策树的核心.

[切分点选择: 最小二乘法]; [输出值: 单元内均值].

1. 原理

假设 X \mathrm{X} X 和 Y \mathrm{Y} Y 分别为输入和输出变量, 并且 Y \mathrm{Y} Y 是连续变量, 给定训练数据集为 D = \mathrm{D}= D= { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } \left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{N}, y_{N}\right)\right\} {(x1​,y1​),(x2​,y2​),…,(xN​,yN​)}, 其中 x i = ( x i ( 1 ) , x i ( 2 ) , … , x i ( n ) ) x_{i}=\left(x_{i}^{(1)}, x_{i}^{(2)}, \ldots, x_{i}^{(n)}\right) xi​=(xi(1)​,xi(2)​,…,xi(n)​) 为输入实例(特征向量), n \mathrm{n} n 为特 征个数, i = 1 , 2 , … , N , N \mathrm{i}=1,2, \ldots, \mathrm{N}, \mathrm{N} i=1,2,…,N,N 为样本容量.

对特征空间的划分采用启发式方法, 每次划分逐一考察当前集合中所有特征的所有取值, 根据平方误差最小化准则选择其中最优的一个作为切分点.如对训练集中第 j j j 个特征变量 x ( j ) x^{(j)} x(j) 和它的取值 s s s, 作为切分变量和切分点, 并定义两个区域 R 1 ( j , s ) = { x ∣ x ( j ) ≤ s } R_{1}(j, s)=\left\{x \mid x^{(j)} \leq s\right\} R1​(j,s)={x∣x(j)≤s} 和 R 2 ( j , s ) = R_{2}(j, s)= R2​(j,s)= { x ∣ x ( j ) > s } \left\{x \mid x^{(j)}>s\right\} {x∣x(j)>s}, 为找出最优的 j \mathrm{j} j 和 s \mathrm{s} s, 对下式求解

min ⁡ j , s [ min ⁡ c 1 ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ) 2 + min ⁡ c 2 ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ) 2 ] \min _{j, s}\left[\min _{c_{1}} \sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-c_{2}\right)^{2}\right] j,smin​⎣⎡​c1​min​xi​∈R1​(j,s)∑​(yi​−c1​)2+c2​min​xi​∈R2​(j,s)∑​(yi​−c2​)2⎦⎤​

也就是找出使要划分的两个区域平方误差和最小的 j j j 和 s s s.

其中, c 1 , c 2 c_{1}, c_{2} c1​,c2​ 为划分后两个区域内固定的输出值, 方括号内的两个 min ⁡ \min min 意为使用的是最 优的 c 1 c_{1} c1​ 和 c 2 c_{2} c2​, 也就是使各自区域内平方误差最小的 c 1 c_{1} c1​ 和 c 2 c_{2} c2​, 易知这两个最优的输出值就是各 自对应区域内 Y Y Y 的均值, 所以上式可写为

min ⁡ j , s [ ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ^ ) 2 + ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ^ ) 2 ] \min _{j, s}\left[\sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-\widehat{c_{1}}\right)^{2}+\sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-\widehat{c_{2}}\right)^{2}\right] j,smin​⎣⎡​xi​∈R1​(j,s)∑​(yi​−c1​ ​)2+xi​∈R2​(j,s)∑​(yi​−c2​ ​)2⎦⎤​

其中 C 1 ^ = 1 N 1 ∑ x i ∈ R 1 ( j , s ) y i , c 2 ^ = 1 N 2 ∑ x i ∈ R 2 ( j , s ) y i \widehat{C_{1}}=\frac{1}{N_{1}} \sum_{x_{i} \in R_{1}(j, s)} y_{i}, \widehat{c_{2}}=\frac{1}{N_{2}} \sum_{x_{i} \in R_{2}(j, s)} y_{i} C1​ ​=N1​1​∑xi​∈R1​(j,s)​yi​,c2​ ​=N2​1​∑xi​∈R2​(j,s)​yi​.

现证明一维空间中样本均值是最优的输出值 (平方误差最小):

给定一个随机数列 { x 1 , x 2 , … , x n } \left\{x_{1}, x_{2}, \ldots, x_{n}\right\} {x1​,x2​,…,xn​}, 设该空间中最优的输出值为 a a a, 根据最小平方误差准则, 构造 a a a 的函数如下:

F ( a ) = ( x 1 − a ) 2 + ( x 2 − a ) 2 + ⋯ + ( x n − a ) 2 \mathrm{F}(\mathrm{a})=\left(x_{1}-a\right)^{2}+\left(x_{2}-a\right)^{2}+\cdots+\left(x_{n}-a\right)^{2} F(a)=(x1​−a)2+(x2​−a)2+⋯+(xn​−a)2

考察其单调性,

F ′ ( a ) = − 2 ( x 1 − a ) − 2 ( x 2 − a ) + ⋯ − 2 ( x n − a ) = 2 n a − 2 ∑ i = 1 n x i F^{\prime}(a)=-2\left(x_{1}-a\right)-2\left(x_{2}-a\right)+\cdots-2\left(x_{n}-a\right)=2 n a-2 \sum_{i=1}^{n} x_{i} F′(a)=−2(x1​−a)−2(x2​−a)+⋯−2(xn​−a)=2na−2i=1∑n​xi​

令 F ′ ( a ) = 0 F^{\prime}(a)=0 F′(a)=0 得, a = 1 n ∑ i = 1 n x i a=\frac{1}{n} \sum_{i=1}^{n} x_{i} a=n1​∑i=1n​xi​

根据其单调性, 易知 a ^ = 1 n ∑ i = 1 n x i \hat{a}=\frac{1}{n} \sum_{i=1}^{n} x_{i} a^=n1​∑i=1n​xi​ 为最小值点.证毕.

找到最优的切分点 ( j , s ) (j, s) (j,s) 后, 依次将输入空间划分为两个区域, 接着对每个区域重复上述 划分过程, 直到满足停止条件为止.这样就生成 了一棵回归树, 这样的回归树通常称为最 小二乘回归树.

2. 算法叙述

输入: 训练数据集 D;

输出: 回归树 f ( x ) f(x) f(x).

在训练数据集所在的输入空间中, 递归地将每个区域划分为两个子区域并决定每个子区域上 的输出值, 构建二叉决策树:

(1) 选择最优切分变量 j \mathrm{j} j 与切分点 s \mathrm{s} s, 求解

min ⁡ j , s [ min ⁡ c 1 ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ) 2 + min ⁡ c 2 ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ) 2 ] \min _{j, s}\left[\min _{c_{1}} \sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-c_{2}\right)^{2}\right] j,smin​⎣⎡​c1​min​xi​∈R1​(j,s)∑​(yi​−c1​)2+c2​min​xi​∈R2​(j,s)∑​(yi​−c2​)2⎦⎤​

遍历变量 j \mathrm{j} j, 对固定的切分变量 j \mathrm{j} j 扫描切分点 s \mathrm{s} s, 选择使上式达到最小值的对 ( j , s ) (j, s) (j,s).

(2) 用选定的对 ( j , s ) (j, s) (j,s) 划分区域并决定相应的输出值:

c m ^ = 1 N m ∑ x i ∈ R m ( j , s ) y i , x ∈ R m ,   m = 1 , 2 \widehat{c_{m}}=\frac{1}{N_{m}} \sum_{x_{i} \in R_{m}(j, s)} y_{i}, \quad \mathrm{x} \in R_{m}, \mathrm{~m}=1,2 cm​ ​=Nm​1​xi​∈Rm​(j,s)∑​yi​,x∈Rm​, m=1,2

其中, R 1 ( j , s ) = { x ∣ x ( j ) ≤ s } , R 2 ( j , s ) = { x ∣ x ( j ) > s } R_{1}(j, s)=\left\{x \mid x^{(j)} \leq s\right\}, R_{2}(j, s)=\left\{x \mid x^{(j)}>s\right\} R1​(j,s)={x∣x(j)≤s},R2​(j,s)={x∣x(j)>s}.

(3) 继续对两个子区域调用步骤(1),(2), 直至满足停止条件.

(4) 将输入空间划分为 M M M 个区域 R 1 , R 1 , … , R M R_{1}, R_{1}, \ldots, R_{M} R1​,R1​,…,RM​, 生成决策树:

f ( x ) = ∑ m = 1 M c m ^ I ( x ∈ R m ) \mathrm{f}(\mathrm{x})=\sum_{m=1}^{M} \widehat{c_{m}} I\left(x \in R_{m}\right) f(x)=m=1∑M​cm​ ​I(x∈Rm​)

其中 I I I 为指示函数, I = { 1  if  ( x ∈ R m ) 0  if  ( x ∉ R m ) \mathrm{I}=\left\{\begin{array}{l}1 \text { if }\left(x \in R_{m}\right) \\ 0 \text { if }\left(x \notin R_{m}\right)\end{array}\right. I={1 if (x∈Rm​)0 if (x∈/​Rm​)​

三、示例

下表为训练数据集, 特征向量只有一维, 根据此数据表建立回归决策树.

x12345678910
y5.565.75.916.46.87.058.98.799.05

(1) 选择最优切分变量 j \mathrm{j} j 与最优切分点 s \mathrm{s} s : 在本数据集中, 只有一个特征变量, 最优切分变量自然是 x \mathrm{x} x .接下来考虑 9 个切分点 { 1.5 , 2.5 , 3.5 , 4.5 , 5.5 , 6.5 , 7.5 , 8.5 , 9.5 } \{1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5\} {1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5} (切分变量两个相邻取值区间 [ a i , a i + 1 \left[a^{i}, a^{i+1}\right. [ai,ai+1 ) 内任一点均可), 根据式计算每个待切分点的损失函数值:

损失函数为

L ( j , s ) = ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ^ ) 2 + ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ^ ) 2 L(j, s)=\sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-\widehat{c_{1}}\right)^{2}+\sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-\widehat{c_{2}}\right)^{2} L(j,s)=xi​∈R1​(j,s)∑​(yi​−c1​ ​)2+xi​∈R2​(j,s)∑​(yi​−c2​ ​)2

其中 c 1 ^ = 1 N 1 ∑ x i ∈ R 1 ( j , s ) y i , c 2 ^ = 1 N 2 ∑ x i ∈ R 2 ( j , s ) y i \widehat{c_{1}}=\frac{1}{N_{1}} \sum_{x_{i} \in R_{1}(j, s)} y_{i}, \widehat{c_{2}}=\frac{1}{N_{2}} \sum_{x_{i} \in R_{2}(j, s)} y_{i} c1​ ​=N1​1​∑xi​∈R1​(j,s)​yi​,c2​ ​=N2​1​∑xi​∈R2​(j,s)​yi​.

a. 计算子区域输出值

当 s = 1.5 \mathrm{s}=1.5 s=1.5 时, 两个子区域 R 1 = { 1 } , R 2 = { 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 } , c 1 = 5.56 \mathrm{R} 1=\{1\}, \mathrm{R} 2=\{2,3,4,5,6,7,8,9,10\}, c_{1}=5.56 R1={1},R2={2,3,4,5,6,7,8,9,10},c1​=5.56,

c 2 = 1 9 ( 5.7 + 5.91 + 6.4 + 6.8 + 7.05 + 8.9 + 8.7 + 9 + 9.05 ) = 7.5 c_{2}=\frac{1}{9}(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)=7.5 c2​=91​(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)=7.5

同理, 得到其他各切分点的子区域输出值, 列表如下

s1.52.53.54.55.56.57.58.59.5
c_(1)5.565.635.725.896.076.246.626.887.11
c_(2)7.57.737.998.258.548.918.929.039.05

b. 计算损失函数值, 找到最优切分点

当 s = 1.5 \mathrm{s}=1.5 s=1.5 时,

L ( 1.5 ) = ( 5.56 − 5.56 ) 2 + [ ( 5.7 − 7.5 ) 2 + ( 5.91 − 7.5 ) 2 + ⋯ + ( 9.05 − 7.5 ) 2 ] = 0 + 15.72 = 15.72 \begin{aligned} \mathrm{L}(1.5) &=(5.56-5.56)^{2}+\left[(5.7-7.5)^{2}+(5.91-7.5)^{2}+\cdots+(9.05-7.5)^{2}\right] \\ &=0+15.72 \\ &=15.72 \end{aligned} L(1.5)​=(5.56−5.56)2+[(5.7−7.5)2+(5.91−7.5)2+⋯+(9.05−7.5)2]=0+15.72=15.72​

同理, 计算得到其他各切分点的损失函数值, 列表如下

s1.52.53.54.55.56.57.58.59.5
L(s)15.7212.078.365.783.911.938.0111.7315.74

易知, 取 s = 6.5 s=6.5 s=6.5 时, 损失函数值最小.因此, 第一个划分点为 ( j = x , s = 6.5 ) (j=x, s=6.5) (j=x,s=6.5).

(2) 用选定的对 ( j , s ) (j, s) (j,s) 划分区域并决定相应的输出值:

划分区域为: R 1 = { 1 , 2 , 3 , 4 , 5 , 6 } , R 2 = { 7 , 8 , 9 , 10 } R_{1}=\{1,2,3,4,5,6\}, R_{2}=\{7,8,9,10\} R1​={1,2,3,4,5,6},R2​={7,8,9,10}

对应输出值: c 1 = 6.24 , c 2 = 8.91 c_{1}=6.24, c_{2}=8.91 c1​=6.24,c2​=8.91

(3) 调用步骤(1),(2), 继续划分:

 对  R 1 , 取切分点  { 1.5 , 2.5 , 3.5 , 4.5 , 5.5 } , 计算得到单元输出值为  \text { 对 } R_{1} \text {, 取切分点 }\{1.5,2.5,3.5,4.5,5.5\} \text {, 计算得到单元输出值为 }  对 R1​, 取切分点 {1.5,2.5,3.5,4.5,5.5}, 计算得到单元输出值为 

s1.52.53.54.55.5
c_(1)5.565.635.725.896.07
c_(2)6.376.546.756.937.05

损失函数值为

s1.52.53.54.55.5
L(s)1.30870.7540.27710.43681.0644

L ( 3.5 ) L(3.5) L(3.5) 最小, 取 s = 3.5 s=3.5 s=3.5 为划分点.

后面同理.

(4) 生成回归树:

假设两次划分后即停止, 则最终生成的回归树为:

T = { 5.72 , x ≤ 3.5 6.75 , 3.5 < x ≤ 6.5 8.91 , x > 6.5 \mathrm{T}=\left\{\begin{array}{cc} 5.72, & x \leq 3.5 \\ 6.75, & 3.5<x \leq 6.5 \\ 8.91, & x>6.5 \end{array}\right. T=⎩⎨⎧​5.72,6.75,8.91,​x≤3.53.5<x≤6.5x>6.5​

四. Python 实现

对第三部分例子的 python 实现及与线性回归对比.
程序源代码

# 开发者:    Leo 刘
# 开发环境: macOs Big Sur
# 开发时间: 2021/11/23 12:48 下午
# 邮箱  : 517093978@qq.com
# @Software: PyCharm
# ----------------------------------------------------------------------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn import linear_model

# Data set
x = np.array(list(range(1, 11))).reshape(-1, 1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05]).ravel()

# Fit regression model
model1 = DecisionTreeRegressor(max_depth=1)
model2 = DecisionTreeRegressor(max_depth=3)
model3 = linear_model.LinearRegression()
model1.fit(x, y)
model2.fit(x, y)
model3.fit(x, y)

# Predict
X_test = np.arange(0.0, 10.0, 0.01)[:, np.newaxis]
y_1 = model1.predict(X_test)
y_2 = model2.predict(X_test)
y_3 = model3.predict(X_test)

# Plot the results
plt.figure()
plt.scatter(x, y, s=20, edgecolor="black",
            c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue",
         label="max_depth=1", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=3", linewidth=2)
plt.plot(X_test, y_3, color='red', label='liner regression', linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()

运行结果:

Decision Tree Regression

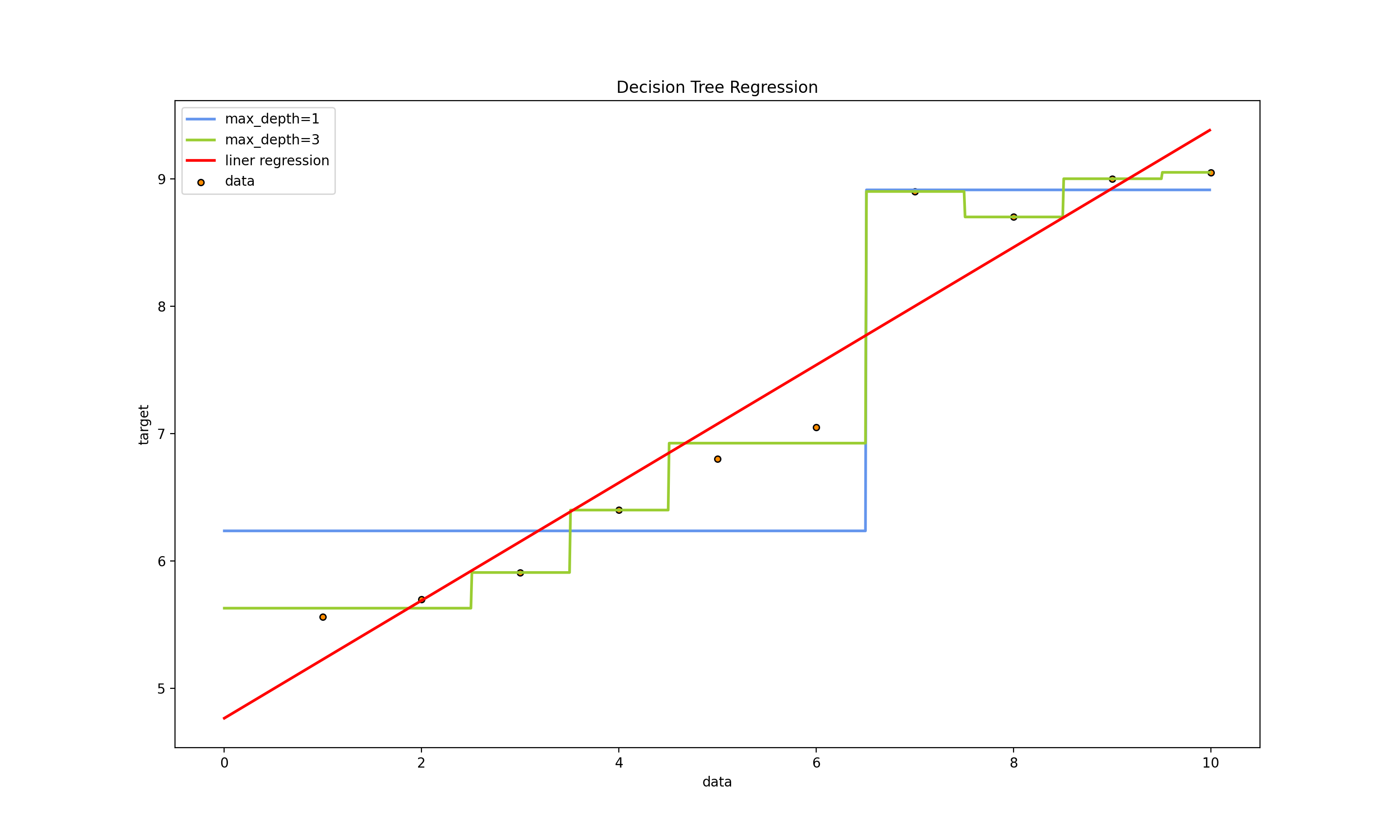
Figure_1

问题三: 模型评估方法

要求: 常见模型评估方法有哪些,对比说明这些方法的基本原理,并举例说明应用范畴及其特点.

没有测量，就没有科学.”这是科学家门捷列夫的名言.在计算机科学特别 是机器学习领域中，对模型的评估同样至关重要.只有选择与问题相匹配的评估方法，才能快速地发现模型选择或训练过程中出现的问题，迭代地对模型进行优化.模型评估主要分为离线评估和在线评估两个阶段.针对分类、排序、回归、 序列预测等不同类型的机器学习问题，评估指标的选择也有所不同.知道每种评 估指标的精确定义、有针对性地选择合适的评估指标、根据评估指标的反馈进行模型调整，这些都是机器学习在模型评估阶段的关键问题，也是一名合格的算法工程师应当具备的基本功.

问题1　准确率的局限性.

京东的奢侈品广告主们希望把广告定向投放给奢侈品用户.京东通过第三方的数据管理平台（Data Management Platform，DMP）拿到了一部分奢侈品用户的数据，并以此为训练集和测试集，训练和测试奢侈品用户的分类模型.该模型的 分类准确率超过了95%，但在实际广告投放过程中，该模型还是把大部分广告投给 了非奢侈品用户，这可能是什么原因造成的？
分析与解答

在解答该问题之前，我们先回顾一下分类准确率的定义.准确率是指分类正 确的样本占总样本个数的比例，即

A c c u r a c y = n correct  n total  Accuracy =\frac{n_{\text {correct }}}{n_{\text {total }}} Accuracy=ntotal ​ncorrect ​​

其中 n correct  n_{\text {correct }} ncorrect ​ 为被正确分类的样本个数, n total  n_{\text {total }} ntotal ​ 为总样本的个数.

准确率是分类问题中最简单也是最直观的评价指标, 但存在明显的缺陷.比如, 当负样本占 99 % 99 \% 99% 时, 分类器把所有样本都预测为负样本也可以获得 99 % 99 \% 99% 的准确率.所以, 当不同类别的样本比例非常不均衡时, 占比大的类别往往成为影响准确率的最主要因素.
明确了这一点, 这个问题也就迎刃而解了.显然, 奢侈品用户只占京东全体用户的一小部分, 虽然模型的整体分类准确率高, 但是不代表对奢侈品用户的分类准确率也很高.在线上投放过程中, 我们只会对模型判定的“奢侈品用户”进行投放, 因此, 对 “奢侈品用户” 判定的准确率不够高的问题就被放大了.为了解决 这个问题, 可以使用更为有效的平均准确率 (每个类别下的样本准确率的算术平 均) 作为模型评估的指标.
事实上, 这是一道比较开放的问题, 面试者可以根据遇到的问题一步步地排 查原因.标准答案其实也不限于指标的选择, 即使评估指标选择对了, 仍会存在 模型过拟合或欠拟合、测试集和训练集划分不合理、线下评估与线上测试的样本 分布存在差异等一系列问题, 但评估指标的选择是最容易被发现, 也是最可能影响评估结果的因素.

问题2　精确率与召回率的权衡.

京东提供视频的模糊搜索功能，搜索排序模型返回的Top 5的精确率非常高， 但在实际使用过程中，用户还是经常找不到想要的视频，特别是一些比较冷门的剧集，这可能是哪个环节出了问题呢？

分析与解答

要回答这个问题，首先要明确两个概念，精确率和召回率.精确率是指分类 正确的正样本个数占分类器判定为正样本的样本个数的比例.召回率是指分类正 确的正样本个数占真正的正样本个数的比例.

在排序问题中，通常没有一个确定的阈值把得到的结果直接判定为正样本或 负样本，而是采用Top N返回结果的Precision值和Recall值来衡量排序模型的性 能，即认为模型返回的Top N的结果就是模型判定的正样本，然后计算前N个位置 上的准确率Precision@N和前N个位置上的召回率Recall@N.

Precision值和Recall值是既矛盾又统一的两个指标，为了提高Precision值，分类器需要尽量在“更有把握”时才把样本预测为正样本，但此时往往会因为过于保守而漏掉很多“没有把握”的正样本，导致Recall值降低.

问题3　ROC曲线

ROC曲线是Receiver Operating Characteristic Curve的简称, 中文名为“受试者工 作特征曲线”.ROC曲线源于军事领域, 而后在医学领域应用甚广, “受试者工作特征曲线”这一名称也正是来自于医学领域.

ROC曲线的横坐标为假阳性率 (False Positive Rate, FPR); 纵坐标为真阳性率 (True Positive Rate, TPR).FPR和TPR的计算方法分别为
F P R = F P N , F P R=\frac{F P}{N}, FPR=NFP​,
T P R = T P P . T P R=\frac{T P}{P} . TPR=PTP​.

上式中, P P P 是真实的正样本的数量, N N N 是真实的负样本的数量, T P T P TP 是 P P P 个正样本中 被分类器预测为正样本的个数, F P F P FP 是 N N N 个负样本中被分类器预测为正样本的个 数.
只看定义确实有点绕, 为了更直观地说明这个问题, 我们举一个医院诊断病 人的例子.假设有 10 位疑似癌症患者, 其中有 3 位很不幸确实患了癌症 ( P = 3 ) (P=3) (P=3), 另外7位不是癌症患者 ( N = 7 ) (N=7) (N=7) .医院对这 10 位疑似患者做了诊断, 诊断出 3 位癌症 患者, 其中有 2 位确实是真正的患者 ( T P = 2 ) (T P=2) (TP=2) .那么真阳性率 T P R = T P / P = 2 / 3 T P R=T P / P=2 / 3 TPR=TP/P=2/3 .对 于 7 位非癌症患者来说, 有一位很不幸被误诊为癌症患者 （ F P = 1 ） （ F P=1 ） （FP=1）, 那么假阳性率 F P R = F P / N = 1 / 7 F P R=F P / N=1 / 7 FPR=FP/N=1/7 .对于“该医院”这个分类器来说, 这组分类结果就对应ROC曲线上 的一个点 ( 1 / 7 , 2 / 3 ) (1 / 7,2 / 3) (1/7,2/3) .

事实上，ROC曲线是通过不断移动分类器的“截断点”来生成曲线上的一组关键点的，通过下面的例子进一步来解释“截断点”的概念.

在二值分类问题中，模型的输出一般都是预测样本为正例的概率.假设测试集中有20个样本，表2.1是模型的输出结果.样本按照预测概率从高到低排序.在输出最终的正例、负例之前，我们需要指定一个阈值，预测概率大于该阈值的样本会被判为正例，小于该阈值的样本则会被判为负例.比如，指定阈值为0.9，那 么只有第一个样本会被预测为正例，其他全部都是负例.上面所说的“截断点”指 的就是区分正负预测结果的阈值.

通过动态地调整截断点，从最高的得分开始（实际上是从正无穷开始，对应着ROC曲线的零点），逐渐调整到最低得分，每一个截断点都会对应一个FPR和 TPR，在ROC图上绘制出每个截断点对应的位置，再连接所有点就得到最终的ROC曲线.

问题4　ROC曲线相比P-R曲线有什么特点？

相比 P-R曲线，ROC曲线有一个特点，当正负样本的分布发生变化时，ROC曲线的形状 能够基本保持不变，而P-R曲线的形状一般会发生较剧烈的变化.

这个特点 让ROC曲线能够尽量降低不同测试集带来的干扰，更加客观地衡量模型本身的性 能.这有什么实际意义呢？在很多实际问题中，正负样本数量往往很不均衡.比如，计算广告领域经常涉及转化率模型，正样本的数量往往是负样本数量的1/1000 甚至1/10000.若选择不同的测试集，P-R曲线的变化就会非常大，而ROC曲线则能够更加稳定地反映模型本身的好坏.所以，ROC曲线的适用场景更多，被广泛用于排序、推荐、广告等领域.但需要注意的是，选择P-R曲线还是ROC曲线是因实际问题而异的，如果研究者希望更多地看到模型在特定数据集上的表现，P-R曲线则能够更直观地反映其性能.

问题5　在对模型进行过充分的离线评估之后，为什么还要进行在线A/B测试？

分析与解答

需要进行在线A/B测试的原因如下.

（1）离线评估无法完全消除模型过拟合的影响，因此，得出的离线评估结果 无法完全替代线上评估结果.

（2）离线评估无法完全还原线上的工程环境.一般来讲，离线评估往往不会 考虑线上环境的延迟、数据丢失、标签数据缺失等情况.因此，离线评估的结果 是理想工程环境下的结果.

（3）线上系统的某些商业指标在离线评估中无法计算.离线评估一般是针对 模型本身进行评估，而与模型相关的其他指标，特别是商业指标，往往无法直接 获得.比如，上线了新的推荐算法，离线评估往往关注的是ROC曲线、P-R曲线等 的改进，而线上评估可以全面了解该推荐算法带来的用户点击率、留存时长、PV 访问量等的变化.这些都要由A/B测试来进行全面的评估.

问题6　在模型评估过程中，有哪些主要的验证方法，它们的优缺点是什么?

场景描述

在机器学习中，我们通常把样本分为训练集和测试集，训练集用于训练模型，测试集用于评估模型.在样本划分和模型验证的过程中，存在着不同的抽样 方法和验证方法.本小节主要考察面试者是否熟知这些方法及其优缺点、是否能 够在不同问题中挑选合适的评估方法.

■ Holdout检验

Holdout 检验是最简单也是最直接的验证方法，它将原始的样本集合随机划分 成训练集和验证集两部分.比方说，对于一个点击率预测模型，我们把样本按照 70%～30% 的比例分成两部分，70% 的样本用于模型训练；30% 的样本用于模型 验证，包括绘制ROC曲线、计算精确率和召回率等指标来评估模型性能.

Holdout 检验的缺点很明显，即在验证集上计算出来的最后评估指标与原始分 组有很大关系.为了消除随机性，研究者们引入了“交叉检验”的思想.

■ 交叉检验

k-fold交叉验证：首先将全部样本划分成k个大小相等的样本子集；依次遍历 这k个子集，每次把当前子集作为验证集，其余所有子集作为训练集，进行模型的 训练和评估；最后把k次评估指标的平均值作为最终的评估指标.在实际实验 中，k经常取10.

留一验证：每次留下1个样本作为验证集，其余所有样本作为测试集.样本总数为n，依次对n个样本进行遍历，进行n次验证，再将评估指标求平均值得到最终 的评估指标.在样本总数较多的情况下，留一验证法的时间开销极大.事实上， 留一验证是留p验证的特例.留p验证是每次留下p个样本作为验证集，而从n个元 素中选择p个元素有 种可能，因此它的时间开销更是远远高于留一验证，故而很 少在实际工程中被应用.

■ 自助法

不管是Holdout检验还是交叉检验，都是基于划分训练集和测试集的方法进行 模型评估的.然而，当样本规模比较小时，将样本集进行划分会让训练集进一步 减小，这可能会影响模型训练效果.有没有能维持训练集样本规模的验证方法 呢？自助法可以比较好地解决这个问题.

自助法是基于自助采样法的检验方法.对于总数为n的样本集合，进行n次有 放回的随机抽样，得到大小为n的训练集.n次采样过程中，有的样本会被重复采 样，有的样本没有被抽出过，将这些没有被抽出的样本作为验证集，进行模型验 证，这就是自助法的验证过程.

问题四: 神经网络

要求: 构建神经网络,实现“与”“或”“非”“异或”运算,系统阐述BP神经网络结构原理,用类C语言(或Python)写出误差传播算法.

问题1 构建神经网络,实现“与”“或”“非”“异或”运算

计算机通常使用数字 1 表示真，使用数字 0 表示假.下列的表格使用 这种相对简洁的表示方法， 基于输入值 A 和输入值 B 的所有组合， 表示 了逻辑 AND 和 OR 函数.

输入值 A输入值 B逻辑 AND逻辑 OR
0000
0101
1001
1111

你可以很清楚地看到， 只有 A 和 B 同时为真时，AND 函数才为真. 同样，你也可以看到，只要 A 和 B 有一个为真时，OR 就为真.

在计算机科学中，布尔逻辑函数非常重要.事实上，最早的电子计算 机就是使用执行这些逻辑函数的微电路构造的.即使是算术，也是使用这 些本身很简单的布尔逻辑函数的电路组合来完成的.

想象一下，不论数据是否由布尔逻辑函数控制，使用简单的线性分类 器就可以从训练数据中学习.对于试图在一些观察和另一些观察之间找到 因果关系或相关关系的科学家而言，这是很自然也是很有用的一种工具. 例如，在下雨时 AND（并且）温度高于 35 摄氏度时，有更多疟疾病人吗？ 当这两个条件（布尔 OR）有任何一个条件为真时，有更多疟疾病人吗？

请看下图， 这幅图在坐标系中显示了两个输入值 A 和 B 与逻辑函数 的关系.这幅图显示，只有当两个输入均为真时，即具有值 1 时，输出才 为真，使用绿色表示.否则输出为假，显示为红色.


你还可以看到一条直线， 将绿色区域和红色区域划分开来. 正如 我们先前完成的演示， 这条直线是线性分类器可以学习到的一个线性 函数.

在这个例子中，数字计算没有本质上的不同，因此我们就不像先前一 样进行数字计算了.

事实上，有许多不同的分界线，也可以很好地对区域进行划分，但是，主 要的一点是，对于形如 y = ax + b 的简单的线性分类器，确实可以学习到布尔 AND 函数.

现在，观察使用类似的方式绘制出的布尔 OR 函数：


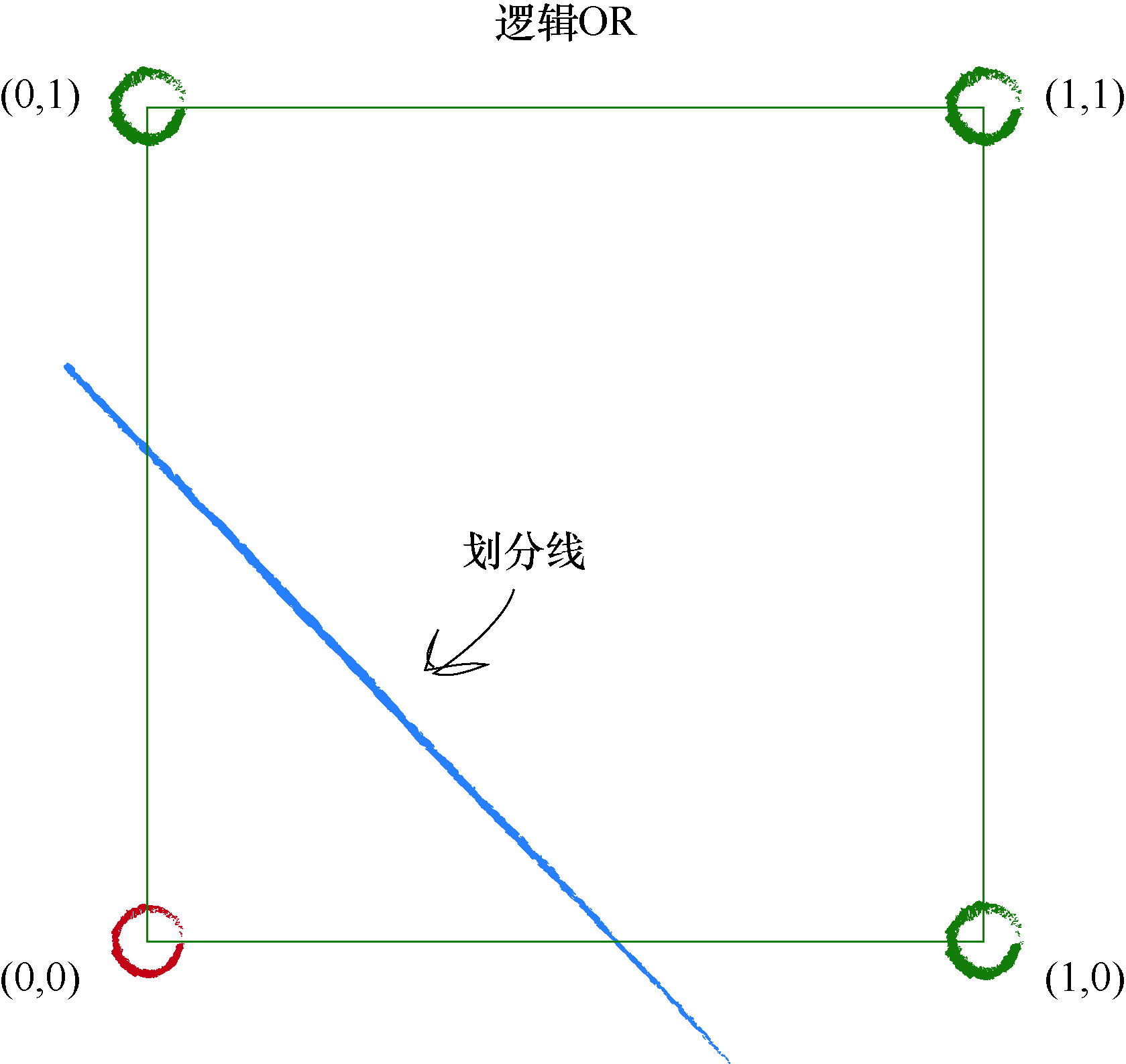
此时，由于仅有点（0,0）对应于输入 A 和 B 同时为假的情况，因此只有这个点是红色的.

所有其他的组合， 至少有一个 A 或 B 为真， 因此输出为真. 这幅图的妙处在于，它清楚地表明了线性分类器也可以学习到布尔 OR 函数.

还有另一种布尔函数称为 XOR，这是 eXclusive OR（异或）的缩写，这种函数只有在 A 或 B 仅有一个为真但两个输入不同时为真的情况下，才输出为真.也就是说，当两个输入都为假或都为真时，输出为假.下表总结了这一点.

输入 A输入 B逻辑 XOR
000
011
101
110

现在，观察这个函数的图，其中网格节点上的输出已经画上颜色了.

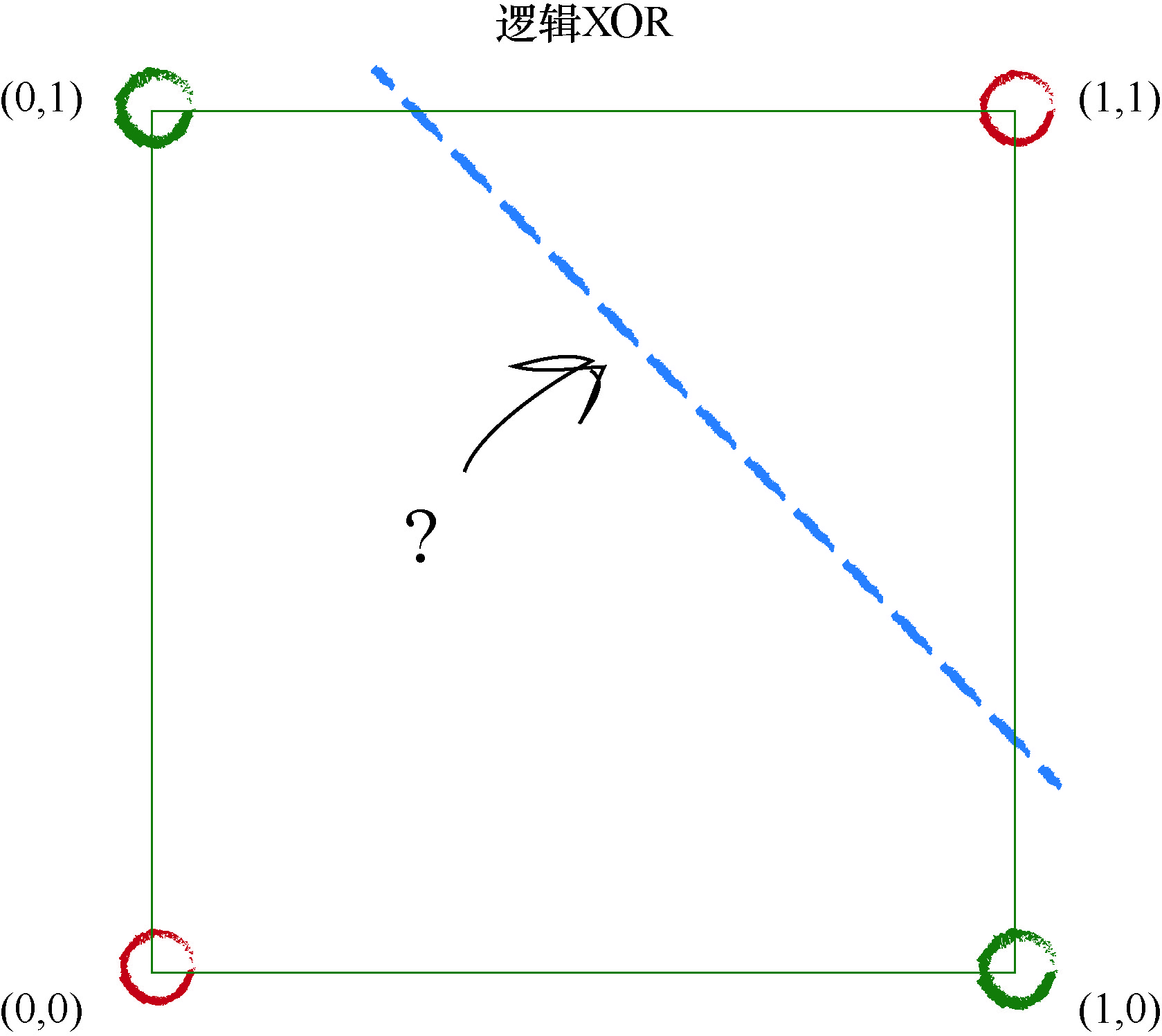
这是一个挑战！我们似乎不能只用一条单一的直线将红色区域和蓝 色区域划分开来.

事实上，对于布尔 XOR 函数而言，不可能使用一条单一的直线成功 地将红色区域和蓝色区域划分开来. 也就是说， 如果出现的是由 XOR 函数支配的训练数据，那么一个简单的线性分类器无法学习到布尔 XOR 函数.

我们已经说明了简单的线性分类器的一个主要限制.如果不能用一条 直线把根本性的问题划分开来，那么简单的线性分类器是没有用处的.

在一些任务中，根本性问题不是线性可分的，也就是说单一的一条直 线于事无补，而我们希望神经网络能够解决此类的任务.

因此，我们需要一种解决的办法.

好在解决的办法很容易，下图使用两条直线对不同的区域进行划分. 这暗示了一种解决的办法， 也就是说， 我们可以使用多个分类器一起工 作.这是神经网络的核心思想.你可以想象，多条直线可以分离出异常形 状的区域，对各个区域进行分类.


关键点

如果数据本身不是由单一线性过程支配，那么一个简单的线性分类器不能对数据进行划分.例如，由逻辑XOR运算符支配的数据说 明了这一点. 但是解决方案很容易，你只需要使用多个线性分类器来划分由单一直线无法分离的数据.

问题2 系统阐述BP神经网络结构原理,用类C语言(或Python)写出误差传播算法.

下图显示了具有 2 个输入节点和 2 个输出节点的简单网络.

两个输出节点都有误差一一事实上, 在末受过训练的神经网络中, 这是极有可能发生的情况.你会发现, 在网络中, 我们需要使用这两个误差 值来告知如何调整内部链接权重.我们可以使用与先前一样的方法, 也就 是跨越造成误差的多条链接, 按照权重比例, 分割输出节点的误差.

我们拥有多个节点这一事实并没有改变任何事情.对于第二个输出节点, 我们只是简单地重复第一个节点所做的事情.为什么如此简单呢? 这 是由于进入输出节点的链接不依赖于到另一个输出节点的链接, 因此事情 就变得非常简单, 在两组的链接之间也不存在依赖关系.

让我们再次观察此图, 我们将第一个输出节点的误差标记为 e 1 \mathrm{e}_{1} e1​ .请记 住, 这个值等于由训练数据提供的所期望的输出值 t 1 \mathrm{t}_{1} t1​ 与实际输出值 o 1 \mathrm{o}_{1} o1​ 之 间的差.也就是, e 1 = ( t 1 − o 1 ) e_{1}=\left(t_{1}-o_{1}\right) e1​=(t1​−o1​) .我们将第二个输出节点的误差标记为 e 2 e_{2} e2​ .

从图中, 你可以发现, 按照所连接链接的比例, 也就是权重 w 1 , 1 \mathrm{w}_{1,1} w1,1​ 和 w 2 , 1 \mathrm{w}_{2,1} w2,1​, 我 们对误差 e 1 e_{1} e1​ 进行了分割.类似地, 我们按照权重 w 1 , 2 w_{1,2} w1,2​ 和 w 2 , 2 w_{2,2} w2,2​ 的比例分割了 e 2 e_{2} e2​ .

让我们写出这些分割值, 这样我们就不会有任何疑问了.我们使用误差 e 1 e_{1} e1​ 的信息, 来调整权重 w 1 , 1 w_{1,1} w1,1​ 和 w 2 , 1 w_{2,1} w2,1​ .通过这种分割方式, 我们使用 e 1 e_{1} e1​ 的一部分来更新 w 1 , 1 w_{1,1} w1,1​ :
w 2 , 1 w 1 , 1 + w 2 , 1 \frac{w_{2,1}}{w_{1,1}+w_{2,1}} w1,1​+w2,1​w2,1​​
类似地, 用来调整 w 2 , 1 \mathrm{w}_{2,1} w2,1​ 的 e 1 \mathrm{e}_{1} e1​ 部分为:
w 1 , 1 w 1 , 1 + w 2 , 1 \frac{w_{1,1}}{w_{1,1}+w_{2,1}} w1,1​+w2,1​w1,1​​
这些分数看起来可能令人有点费解, 让我们详细阐释这些分数.在所有这些符号背后, 思想非常简单, 也就是误差 e 1 e_{1} e1​ 要分割更大的值给较大的 权重, 分割较小的值给较小的权重.

如果 w 1 , 1 \mathrm{w}_{1,1} w1,1​ 是 w 2 , 1 \mathrm{w}_{2,1} w2,1​ 的 2 倍, 比如说, w 1 , 1 = 6 , w 2 , 1 = 3 \mathrm{w}_{1,1}=6, \mathrm{w}_{2,1}=3 w1,1​=6,w2,1​=3, 那么用于更新 w 1 , 1 \mathrm{w}_{1,1} w1,1​ 的 e 1 e_{1} e1​ 的部分就是 6 / ( 6 + 3 ) = 6 / 9 = 2 / 3 6 /(6+3)=6 / 9=2 / 3 6/(6+3)=6/9=2/3 . 同时, 这留下了 1 / 3 1 / 3 1/3 的 e 1 e_{1} e1​ 给较小的 权重 w 2 , 1 \mathrm{w}_{2,1} w2,1​, 我们可以通过表达式 3 / ( 6 + 3 ) = 3 / 9 3 /(6+3)=3 / 9 3/(6+3)=3/9 确认这确实是 1 / 3 1 / 3 1/3 .

如果权重相等, 正如你所期望的, 各分一半.让我们确定一下, 假设 w 1 , 1 = \mathrm{w}_{1,1}= w1,1​= 4 和 w 2 , 1 = 4 \mathrm{w}_{2,1}=4 w2,1​=4, 那么针对这种情况, e 1 \mathrm{e}_{1} e1​ 所分割的比例都等于 4 / ( 4 + 4 ) = 4 / 8 = 1 / 2 4 /(4+4)=4 / 8=1 / 2 4/(4+4)=4/8=1/2 .

在更加深入理解之前, 让我们先暂停一下, 退后一步, 从一个较远的 距离观察我们已经做的事情.我们知道需要使用误差来指导在网络内部如 何调整一些参数, 在这里也就是链接权重.我们明白了如何调整链接权 重, 并且我们使用链接权重来调节进入神经网络最终输出层的信号.在存 在多个输出节点的情况下, 我们也看到了这种调整过程没有变得复杂, 只 是对每个输出节点都进行相同的操作.然后就搞定了!

接下来我们要问的问题是, 当神经网络多于 2 层时, 会发生什么事情 呢? 在离最终输出层相对较远的层中, 我们如何更新链接权重呢?

下图显示了具有 3 层的简单神经网络，一个输入层、一个隐藏层和一个最终输出层.


从右手边的最终输出层开始，往回工作，我们可以看到，我们使用在输出层的误差值引导调整馈送到最终层的链接权重.更一般地，我们将输出误差标记为 e o u t p u t e_{output} eoutput​ ，将在输出层和隐藏层之间的链接权重标记为 w h o w_{ho} who​ .通 过将误差值按权重的比例进行分割，我们计算出与每条链接相关的特定误差值.

通过可视化这种方法，我们可以明白，对于额外的新层所需要做的事情.简单说来，我们采用与隐藏层节点相关联的这些误差 e h i d d e n e_{hidden} ehidden​ ，再次将这些误差按照输入层和隐藏层之间的链接权重 w i h w_{ih} wih​ 进行分割.下图就显示了此逻辑.


如果神经网络具有多个层，那么我们就从最终输出层往回工作，对每 一层重复应用相同的思路.误差信息流具有直观意义.同样，你明白为什么我们称之为误差的反向传播了.如果对于输出层节点的 e o u t p u t e_{output} eoutput​ ，我们首先使用了输出误差.那么，对于隐藏层节点 e h i d d e n e_{hidden} ehidden​ ，我们使用什么误差呢？中间隐藏层节点没有明确显示的误差，因此这是一个好问题.我们知道，向前馈送输入信号，隐藏层的每个节点确实有一个单一的输出.还记得，我们在该节点经过加权求和的信号上应用激活函数，才得到了这个输出.但是，我们如何才能计算出误差呢？

对于隐藏层的节点，我们没有目标值或所希望的输出值.我们只有最 终输出层节点的目标值，这个目标值来自于训练样本数据.让我们再次观察上图，寻找一些灵感！隐藏层第一个节点具有两个链接，这两个链接将这个节点连接到两个输出层节点.我们知道，沿着各个链接可以分割输出 误差， 就像我们先前所做的一样.这意味着，对于中间层节点的每个链接，我们得到了某种误差值.我们可以重组这两个链接的误差，形成这个节点的误差.实际上我们没有中间层节点的目标值，因此这种方法算得上第二最佳方法.下图就可视化了这种想法.


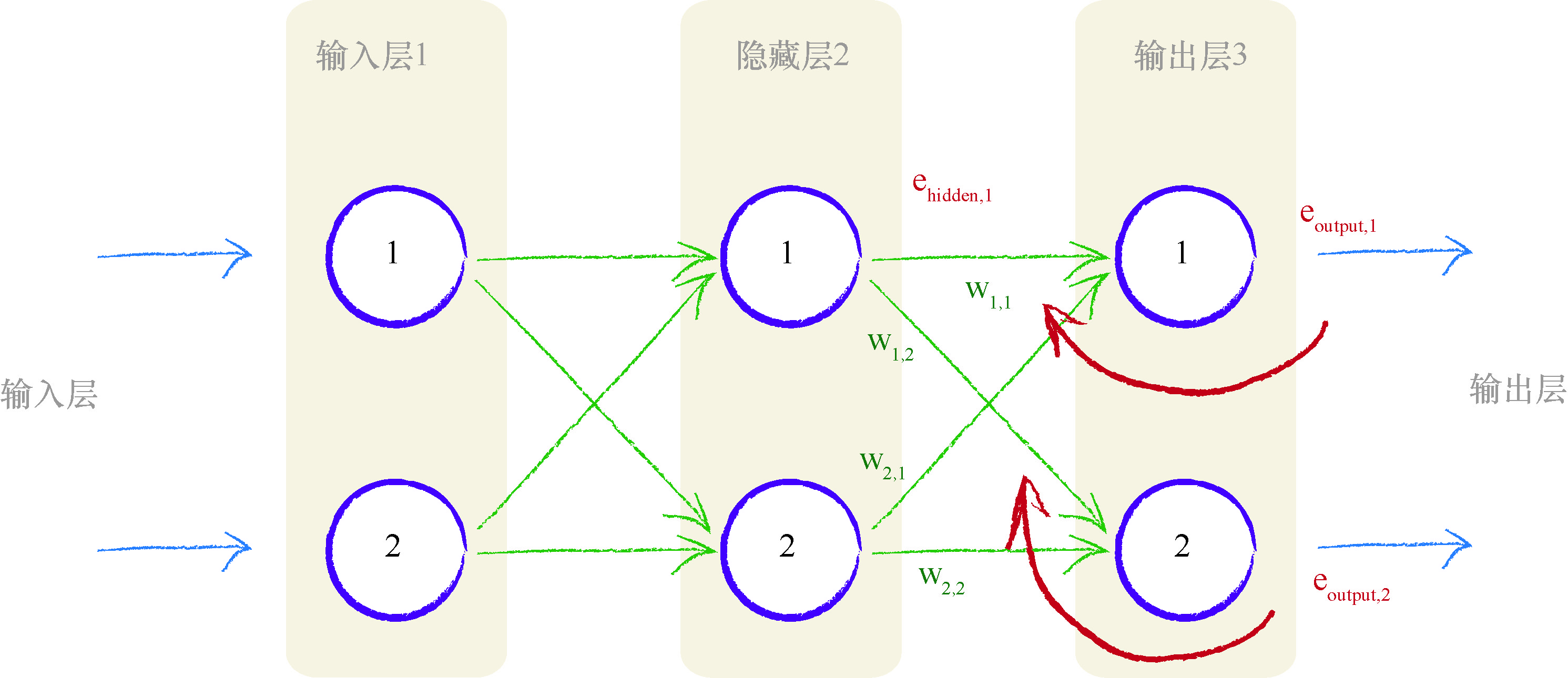
虽然你可以相对清楚地观察到发生的事情，但是我们还是要再次演示， 确认一下.我们需要隐藏层节点的误差，这样我们就可以使用这个误差更新 前一层中的权重.我们称这个误差为 $e_{hidden} .但是，我们不需要明确地回答这 些误差是什么.我们的训练样本数据只给出了最终输出节点的目标值，因此 不能说这个误差等于中间层节点所需目标输出值与实际输出值之间的差.

训练样本数据只告诉我们最终输出节点的输出应该为多少，而没有告诉我们任何其他层节点的输出应该是多少.这是这道谜题的核心. 我们可以使用先前所看到的误差反向传播，为链接重组分割的误差. 因此，第一个隐藏层节点的误差是与这个节点前向连接所有链接中分割误差的和.在上图中，我们得到了在权重为 w 1 , 1 w_{1,1} w1,1​ 的链接上的输出误差 e o u t p u t , 1 e_{output,1} eoutput,1​ 的一部分，同时也得到了在权重为 w 1 , 2 w_{1,2} w1,2​ 的链接上第二个输出节点的输出误差 e o u t p u t , 2 e_{output,2} eoutput,2​ 的一部分.

让我们将这些值写下来.

e hidden,  1 = e_{\text {hidden, } 1}= ehidden, 1​= 链接 w 1 , 1 w_{1,1} w1,1​ 和链接 w 1 , 2 w_{1,2} w1,2​ 上的分割误差之和
= e output,  , ∗ w 1 , 1 w 1 , 1 + w 2 , 1 + e output,  2 ∗ w 1 , 2 w 1 , 2 + w 2 , 2 =e_{\text {output, },} * \frac{w_{1,1}}{w_{1,1}+w_{2,1}}+\quad e_{\text {output, } 2} * \frac{w_{1,2}}{w_{1,2}+w_{2,2}} =eoutput, ,​∗w1,1​+w2,1​w1,1​​+eoutput, 2​∗w1,2​+w2,2​w1,2​​
这有助于我们看到这个理论的实际作用, 下图详细阐释了在一个简单 的具有实际数字的 3 层网络中, 误差如何向后传播.


让我们演示一下反向传播的误差.你可以观察到，第二个输出层节点 的误差 0.5，在具有权重 1.0 和 4.0 的两个链接之间，根据比例被分割成了 0.1 和 0.4.你也可以观察到，在隐藏层的第二个节点处的重组误差等于连 接的分割误差之和，也就是 0.48 与 0.4 的和，等于 0.88.

如下图所示，我们进一步向后工作，在前一层中应用相同的思路.

关键点

神经网络通过调整链接权重进行学习.这种方法由误差引导，误差就是训练数据所给出正确答案和实际输出之间的差值. 简单地说，在输出节点处的误差等于所需值与实际值之间的差值. 然而，与内部节点相关联的误差并不显而易见.一种方法是按照链接权重的比例来分割输出层的误差，然后在每个内部节点处重组这些误差.

到此为止,已经生动的介绍了神经网络中误差反向传播的BP算法的基本思想,下面结合本人的主要研究方向-‘机器学习求解PDE’,通过Pytorch框架演示神经网络求解微分方程及数值插值和拟合问题.

数学是这样一步步“沦陷”的

引言

近年来，深度学习由于神经网络强大的表示能力在计算机视觉、语音识别和自然语言处理等方面取得了巨大的成功.利用人工神经网络(ANN)进行数值计算来解决各种数学问题引起了大家的广泛研究.例如:

  • 插值、拟合
  • 求解常微分方程(ODE)
  • 求解偏微分非常(PDE)

一、插值
问题描述
在函数 f ( x ) = s i n ( x ) − 0.5 f(x)=sin(x)-0.5 f(x)=sin(x)−0.5, x ∈ ( − 2 π , 2 π ) x\in(-2\pi,2\pi) x∈(−2π,2π)上均匀采样20个点作为插值点,使用 ANN 进行插值的数值计算结果如下:
Interpolation

程序源代码

# 开发者:    Leo 刘
# 开发环境: macOs Big Sur
# 开发时间: 2021/8/1 11:43 上午
# 邮箱  : 517093978@qq.com
# @Software: PyCharm

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from Dynamic_drawing import image2gif

# 构建输入集
x_data = np.linspace(-2 * np.pi, 2 * np.pi, 300)[:, np.newaxis]
x_data = torch.tensor(x_data).float()
y_data = np.sin(x_data) - 0.5
# y_data = np.sin(x_data)*x_data**2 - 0.5
y_data = torch.tensor(y_data).float()


# 定义神经网络
class Net(torch.nn.Module):
    # 初始化数组，参数分别是初始化信息，特征数，隐藏单元数，输出单元数
    def __init__(self, n_feature, n_hidden, n_output):
        # 此步骤是官方要求
        super(Net, self).__init__()
        # 设置输入层到隐藏层的函数
        self.input = torch.nn.Linear(n_feature, n_hidden)
        # 设置隐藏层到隐藏层的函数
        self.hidden = torch.nn.Linear(n_hidden, n_hidden)
        # 设置隐藏层到输出层的函数
        self.predict = torch.nn.Linear(n_hidden, n_output)

        # 定义向前传播函数

    def forward(self, input):
        # 给x加权成为a，用激活函数将a变成特征b
        # input = torch.relu(self.hidden(input))  # 线性插值
        input = torch.tanh(self.input(input))  # 非线性插值
        # 给a加权成为b，用激活函数将b变成特征c
        input = torch.tanh(self.hidden(input))
        # 给c加权，预测最终结果
        input = self.predict(input)
        return input


def interpolation_node(x_inter_data, y_inter_data, N):
    data_size, w = x_data.size()
    b = np.array(range(N))
    a = 1 + data_size / N * b
    x_inter_node = x_inter_data[a]
    y_inter_node = y_inter_data[a]
    return x_inter_node, y_inter_node


# 初始化网络
print('神经网络结构：')
myNet = Net(1, 10, 1)
print(myNet)

# 设置优化器
# optimizer = torch.optim.SGD(myNet.parameters(), lr=0.05)
optimizer = torch.optim.Adam(myNet.parameters(), lr=0.05)
loss_func = nn.MSELoss()

best_loss, best_epoch = 1000, 0
epochs = 2000  # 训练次数
x_inter_node, y_inter_node = interpolation_node(x_data,y_data, 20)  # 获取插值节点
input = x_inter_node
label = y_inter_node
Loss_list = []
print('开始学习：')
for epoch in range(epochs + 1):
    output = myNet(input)
    loss = loss_func(output, label)  # 计算误差
    Loss_list.append(loss / (len(x_data)))
    optimizer.zero_grad()  # 清除梯度
    loss.backward()  # 误差反向传播
    optimizer.step()  # 梯度更新
    torch.save(myNet.state_dict(), 'new_best_interpolation.mdl')
    # 记录误差
    if epoch % 100 == 0:
        print('epoch:', epoch, 'loss:', loss.item(), )
        # 记录最佳训练次数
        if epoch > int(4 * epochs / 5):
            if torch.abs(loss) < best_loss:
                best_loss = torch.abs(loss).item()
                best_epoch = epoch
                torch.save(myNet.state_dict(), 'new_best_interpolation.mdl')

    # 连续绘图
    if epoch % 10 == 0:
        plt.ion()  # 打开交互模式
        plt.close('all')
        myNet.load_state_dict(torch.load('new_best_interpolation.mdl'))
        with torch.no_grad():
            pred = myNet(x_data)
        plt.plot(x_data, y_data, label='real')
        plt.plot(x_data, pred, label='predict')
        plt.title("Training times:" + str(epoch))
        # 画散点图
        colors1 = '#00CED1'  # 点的颜色
        colors2 = '#DC143C'
        area = np.pi * 2 ** 2  # 点面积
        plt.scatter(input, label, s=area, c=colors2, alpha=0.9, label='node')
        plt.legend(loc="upper right")
        plt.savefig('./Training_process/Interpolation_'+str(epoch)+'.png')
        if epoch == best_epoch:
            plt.savefig('Best_nterpolation.png')
        # plt.show()
        # plt.pause(0.01)
print('=' * 55)
print('学习结束'.center(55))
print('-' * 55)
print('最优学习批次:', best_epoch, '最优误差:', best_loss)
plt.close('all')
plt.ioff()  # 关闭交互模式
plt.title('Error curve')
plt.xlabel('loss vs. epoches')
plt.ylabel('loss')
plt.plot(range(0, epochs + 1), Loss_list, label='Loss')
plt.savefig('Error_curve_interpolation.png')
# plt.show()
print('已生成"最优插值结果图"，请打开文件"Best_interpolation.png"查看')
print('已生成"误差曲线图"，请打开文件"Error_curve_interpolation.png"查看')
print('-' * 55)
print('准备绘制训练过程动态图')
image2gif.image2gif('Interpolation')
print('=' * 55)

二、拟合
问题描述
在函数 f ( x ) = s i n ( x ) − 0.5 f(x)=sin(x)-0.5 f(x)=sin(x)−0.5, x ∈ ( − 2 π , 2 π ) x\in(-2\pi,2\pi) x∈(−2π,2π)上添加噪声后,使用 ANN 对300个点进行拟合的数值计算结果如下:

Fitting

程序源代码

# 开发者:    Leo 刘
# 开发环境: macOs Big Sur
# 开发时间: 2021/8/1 11:43 上午
# 邮箱  : 517093978@qq.com
# @Software: PyCharm

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from Dynamic_drawing import image2gif

# 构建输入集
x_data = np.linspace(-2 * np.pi, 2 * np.pi, 300)[:, np.newaxis]
x_data = torch.tensor(x_data).float()
noise = np.random.normal(0, 0.05, x_data.shape)
y_data = np.sin(x_data) - 0.5 + noise
y_data = torch.tensor(y_data).float()


# 定义神经网络
class Net(torch.nn.Module):
    # 初始化数组，参数分别是初始化信息，特征数，隐藏单元数，输出单元数
    def __init__(self, n_feature, n_hidden, n_output):
        # 此步骤是官方要求
        super(Net, self).__init__()
        # 设置输入层到隐藏层的函数
        self.input = torch.nn.Linear(n_feature, n_hidden)
        # 设置隐藏层到隐藏层的函数
        self.hidden = torch.nn.Linear(n_hidden, n_hidden)
        # 设置隐藏层到输出层的函数
        self.predict = torch.nn.Linear(n_hidden, n_output)

        # 定义向前传播函数

    def forward(self, input):
        # 给x加权成为a，用激活函数将a变成特征b
        # input = torch.relu(self.hidden(input))  # 线性插值
        input = torch.tanh(self.input(input))  # 非线性插值
        # 给a加权成为b，用激活函数将b变成特征c
        input = torch.tanh(self.hidden(input))
        # 给c加权，预测最终结果
        input = self.predict(input)
        return input


# 初始化网络
myNet = Net(1, 10, 1)
print('神经网络结构：')
print(myNet)

# 设置优化器
# optimizer = torch.optim.SGD(myNet.parameters(), lr=0.05)
optimizer = torch.optim.Adam(myNet.parameters(), lr=0.05)
loss_func = nn.MSELoss()

best_loss, best_epoch = 1000, 0
epochs = 2000  # 训练次数
input = x_data
label = y_data
Loss_list = []
print('开始学习：')
for epoch in range(epochs + 1):
    output = myNet(input)
    loss = loss_func(output, label)  # 计算误差
    Loss_list.append(loss / (len(x_data)))
    optimizer.zero_grad()  # 清除梯度
    loss.backward()  # 误差反向传播
    optimizer.step()  # 梯度更新
    torch.save(myNet.state_dict(), 'new_best_fitting.mdl')
    # 记录误差
    if epoch % 100 == 0:
        print('epoch:', epoch, 'loss:', loss.item(), )
        # 记录最佳训练次数
        if epoch > int(4 * epochs / 5):
            if torch.abs(loss) < best_loss:
                best_loss = torch.abs(loss).item()
                best_epoch = epoch
                torch.save(myNet.state_dict(), 'new_best_fitting.mdl')

    # 连续绘图
    if epoch % 10 == 0:
        plt.ion()  # 打开交互模式
        plt.close('all')
        myNet.load_state_dict(torch.load('new_best_fitting.mdl'))
        with torch.no_grad():
            pred = myNet(x_data)
        plt.plot(x_data, y_data, label='real')
        plt.plot(x_data, pred, label='predict')
        plt.title("Training times:" + str(epoch))
        plt.legend()
        plt.savefig('./Training_process/Fitting_'+str(epoch)+'.png')
        if epoch == best_epoch:
            plt.savefig('Best_fitting.png')
        # plt.show()
        # plt.pause(0.01)
print('=' * 55)
print('学习结束'.center(55))
print('-' * 55)
print('最优学习批次:', best_epoch, '最优误差:', best_loss)
plt.close('all')
plt.ioff()  # 关闭交互模式
plt.title('Error curve')
plt.xlabel('loss vs. epoches')
plt.ylabel('loss')
plt.plot(range(0, epochs + 1), Loss_list, label='Loss')
plt.savefig('Error_curve_Fitting.png')
# plt.show()
print('已生成"最优拟合结果图"，请打开文件"Best_fitting.png"查看')
print('已生成"误差曲线图"，请打开文件"Error_curve_Fitting.png"查看')
print('-' * 55)
print('准备绘制训练过程动态图')
image2gif.image2gif('Fitting')
print('=' * 55)

三、常微分方程
问题描述
考虑如下常微分方程：
f ( x ) = d ϕ d x + ( x + 1 + 3 x 2 1 + x + x 3 ) ϕ − x 3 − 2 x − x 2 1 + 3 x 2 1 + x + x 3 , x ∈ ( 0 , 2 ) f(x)=\frac{d\phi}{dx} + (x + \frac{1+3x^2}{1+x+x^3})\phi - x^3 - 2x - x^2\frac{1+3x^2}{1+x+x^3}, x\in (0,2) f(x)=dxdϕ​+(x+1+x+x31+3x2​)ϕ−x3−2x−x21+x+x31+3x2​,x∈(0,2)
f ( x ) = 0 , x = 0. f(x) = 0, x=0. f(x)=0,x=0.

ANN求解结果与真解: f ( x ) = e − 1 2 x 2 1 + x + x 3 + x 2 f(x)=\frac{e^{-\frac{1}{2}x^2}}{1+x+x^3}+x^2 f(x)=1+x+x3e−21​x2​+x2的对比如下:

ODE

程序源代码

# 开发者:    Leo 刘
# 开发环境: macOs Big Sur
# 开发时间: 2021/5/21 3:07 下午
# 邮箱  : 517093978@qq.com
# @Software: PyCharm

import matplotlib.pyplot as plt
import numpy as np
import torch
from torch import autograd
from Dynamic_drawing import image2gif

# 构建输入集
# 生成[0,2]区间100个点
x_data = np.linspace(0, 2, 100, endpoint=True)[:, np.newaxis]

x_data = torch.tensor(x_data).float()
# print(x_data.size())
# 已知解析解用于比较
y_data = np.exp(-0.5 * x_data ** 2) / (1 + x_data + x_data ** 3) + x_data ** 2
y_data = torch.tensor(y_data).float()


# 定义神经网络
class Net(torch.nn.Module):
    # 初始化数组，参数分别是初始化信息，特征数，隐藏单元数，输出单元数
    def __init__(self, n_feature, n_hidden, n_output):
        # 此步骤是官方要求
        super(Net, self).__init__()
        # 设置输入层到隐藏层的函数
        self.input = torch.nn.Linear(n_feature, n_hidden)
        # 设置隐藏层到隐藏层的函数
        self.hidden = torch.nn.Linear(n_hidden, n_hidden)
        # 设置隐藏层到输出层的函数
        self.predict = torch.nn.Linear(n_hidden, n_output)

        # 定义向前传播函数

    def forward(self, input):
        # 给x加权成为a，用激活函数将a变成特征b
        # input = torch.relu(self.hidden(input))  # 线性插值
        input = torch.tanh(self.input(input))  # 非线性插值
        # 给a加权成为b，用激活函数将b变成特征c
        input = torch.tanh(self.hidden(input))
        # 给c加权，预测最终结果
        input = self.predict(input)
        return input


# 初始化网络
print('神经网络结构：')
myNet = Net(1, 10, 1)
print(myNet)
# 设置优化器
optimizer = torch.optim.Adam(myNet.parameters(), lr=0.05)

best_loss, best_epoch = 100, 0
epochs = 2000  # 训练次数
input = x_data
# 声明：自动保存参数input的梯度
input.requires_grad_()
Loss_list = []
print('开始学习：')
for epoch in range(epochs + 1):
    output = myNet(input)
    # 梯度
    grads = autograd.grad(outputs=output, inputs=input,
                          grad_outputs=torch.ones_like(output),
                          create_graph=True, retain_graph=True, only_inputs=True)[0]
    lq = (1 + 3 * (input ** 2)) / (1 + input + input ** 3)

    t_loss = (grads + (input + lq) * output - input ** 3 - 2 * input - lq * input * input) ** 2  # 常微分方程F的平方
    loss_func = torch.mean(t_loss) + (output[0] - 1) ** 2  # 每点F平方求和后取平均再加上边界条件
    loss = loss_func  # 计算误差
    Loss_list.append(loss / (len(x_data)))
    optimizer.zero_grad()  # 清除梯度
    loss.backward()  # 误差反向传播
    optimizer.step()  # 梯度更新
    torch.save(myNet.state_dict(), 'new_best_ODE.mdl')
    # 记录误差
    if epoch % 100 == 0:
        print('epoch:', epoch, 'loss:', loss.item(), )
        # 记录最佳训练次数
        if epoch > int(4 * epochs / 5):
            if torch.abs(loss) < best_loss:
                best_loss = torch.abs(loss).item()
                best_epoch = epoch
                torch.save(myNet.state_dict(), 'new_best_ODE.mdl')
    # 连续绘图
    if epoch % 1 == 0:
        plt.ion()  # 打开交互模式
        plt.close('all')
        myNet.load_state_dict(torch.load('new_best_ODE.mdl'))
        with torch.no_grad():
            x_data = np.linspace(0, 2, 100, endpoint=True)[:, np.newaxis]
            x_data = torch.tensor(x_data).float()
            pred = myNet(x_data)
        plt.plot(x_data, y_data, label='real')
        plt.plot(x_data, pred, label='predict')
        plt.title("Training times:" + str(epoch))
        plt.legend()
        plt.savefig('./Training_process/ODE_'+str(epoch)+'.png')
        if epoch == best_epoch:
            plt.savefig('Best_ODE.png')
        # plt.show()
        # plt.pause(0.01)
print('=' * 55)
print('学习结束'.center(55))
print('-' * 55)
print('最优学习批次:', best_epoch, '最优误差:', best_loss)
plt.close('all')
plt.ioff()  # 关闭交互模式
plt.title('Error curve')
plt.xlabel('loss vs. epoches')
plt.ylabel('loss')
plt.plot(range(0, epochs + 1), Loss_list, label='Loss')
plt.savefig('Error_curve_ODE.png')
# plt.show()
print('已生成"最优求解结果图"，请打开文件"Best_ODE.png"查看')
print('已生成"误差曲线图"，请打开文件"Error_curve_ODE.png"查看')
print('-' * 55)
print('准备绘制训练过程动态图')
image2gif.image2gif('ODE')
print('=' * 55)

四、偏微分方程
问题描述
考虑泊松方程：
− Δ u ( x ) = 1 , x ∈ Ω -\Delta u(x) = 1, x\in \Omega −Δu(x)=1,x∈Ω
u ( x ) = 0 , x ∈ ∂ Ω , u(x) = 0, x\in \partial \Omega, u(x)=0,x∈∂Ω,

其中 Ω = ( − 1 , 1 ) × ( − 1 , 1 ) \ [ 0 , 1 ) × { 0 } \Omega = (-1,1) \times (-1,1) \backslash [0,1) \times \{0\} Ω=(−1,1)×(−1,1)\[0,1)×{0}.使用 DRM 算法进行求解的数值计算结果如下:

Deep_Ritz

程序源代码

# 开发者:    Leo 刘
# 开发环境: macOs Big Sur
# 开发时间: 2021/8/1 10:45 下午
# 邮箱  : 517093978@qq.com
# @Software: PyCharm
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch import optim, autograd
from matplotlib import pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
from Dynamic_drawing import image2gif

# Try to solve the poisson equation:
'''  Solve the following PDE
-\Delta u(x) = 1, x\in \Omega,
u(x) = 0, x\in \partial \Omega  
\Omega = (-1,1) * (-1,1) \ [0,1) *{0}
'''


# 定义DRM中提到的激活函数（但会出现异常值，故采用tanh激活函数）
class PowerReLU(nn.Module):
    """
    Implements simga(x)^(power)
    Applies a power of the rectified linear unit element-wise.

    NOTE: inplace may not be working.
    Can set inplace for inplace operation if desired.
    BUT I don't think it is working now.

    INPUT:
        x -- size (N,*) tensor where * is any number of additional
             dimensions
    OUTPUT:
        y -- size (N,*)
    """

    def __init__(self, inplace=False, power=3):
        super(PowerReLU, self).__init__()
        self.inplace = inplace
        self.power = power

    def forward(self, input):
        y = F.relu(input, inplace=self.inplace)
        return torch.pow(y, self.power)


# 定义一个残差块
class Block(nn.Module):
    """
    Implementation of the block used in the Deep Ritz
    Paper

    Parameters:
    in_N  -- dimension of the input
    width -- number of nodes in the interior middle layer
    out_N -- dimension of the output
    phi   -- activation function used
    """

    def __init__(self, in_N, width, out_N, phi=PowerReLU()):
        super(Block, self).__init__()
        # create the necessary linear layers
        self.L1 = nn.Linear(in_N, width)
        self.L2 = nn.Linear(width, out_N)
        # choose appropriate activation function
        self.phi = nn.Tanh()

    def forward(self, x):
        return self.phi(self.L2(self.phi(self.L1(x)))) + x


# 组装残差块，完成一个完整残差神经网络的搭建
class drrnn(nn.Module):
    """
    drrnn -- Deep Ritz Residual Neural Network

    Implements a network with the architecture used in the
    deep ritz method paper

    Parameters:
        in_N  -- input dimension
        out_N -- output dimension
        m     -- width of layers that form blocks
        depth -- number of blocks to be stacked
        phi   -- the activation function
    """

    def __init__(self, in_N, m, out_N, depth=4, phi=PowerReLU()):
        super(drrnn, self).__init__()
        # set parameters
        self.in_N = in_N
        self.m = m
        self.out_N = out_N
        self.depth = depth
        self.phi = nn.Tanh()
        # list for holding all the blocks
        self.stack = nn.ModuleList()

        # add first layer to list
        self.stack.append(nn.Linear(in_N, m))

        # add middle blocks to list
        for i in range(depth):
            self.stack.append(Block(m, m, m))

        # add output linear layer
        self.stack.append(nn.Linear(m, out_N))

    def forward(self, x):
        # first layer
        for i in range(len(self.stack)):
            x = self.stack[i](x)
        return x


# 内部采样
def get_interior_points(N=512, d=2):
    """
    randomly sample N points from interior of [-1,1]^d
    """
    return torch.rand(N, d) * 2 - 1


# 边界采样
def get_boundary_points(N=32):
    """
    randomly sample N points from boundary
    """
    index = torch.rand(N, 1)
    index1 = torch.rand(N, 1) * 2 - 1
    xb1 = torch.cat((index, torch.zeros_like(index)), dim=1)
    xb2 = torch.cat((index1, torch.ones_like(index1)), dim=1)
    xb3 = torch.cat((index1, torch.full_like(index1, -1)), dim=1)
    xb4 = torch.cat((torch.ones_like(index1), index1), dim=1)
    xb5 = torch.cat((torch.full_like(index1, -1), index1), dim=1)
    xb = torch.cat((xb1, xb2, xb3, xb4, xb5), dim=0)

    return xb


# 初始化神经网络参数
def weights_init(m):
    if isinstance(m, (nn.Conv2d, nn.Linear)):
        nn.init.xavier_normal_(m.weight)
        nn.init.constant_(m.bias, 0.0)


epochs = 50000  # 学习次数
in_N = 2
m = 10
out_N = 1

# print(torch.cuda.is_available())
# 优先选用GPU进行训练
device = torch.device('cpu' if torch.cuda.is_available() else 'cpu')
# 实例化残差神经网络模型
model = drrnn(in_N, m, out_N).to(device)
# Apply weight_init initialization method to submodels
model.apply(weights_init)
# 选择Adam优化器，初始化学习率（lr）为3e-3
optimizer = optim.Adam(model.parameters(), lr=3e-3)
print('神经网络结构：')
print(model)

best_loss, best_epoch = 1000, 0
Loss_list = []
# 开始训练
print('开始学习：')
for epoch in range(epochs + 1):

    # 产生数据集
    xr = get_interior_points()
    xb = get_boundary_points()

    xr = xr.to(device)
    xb = xb.to(device)
    # 声明：自动保存参数xr、xb_rho的梯度
    xr.requires_grad_()
    output_r = model(xr)
    output_b = model(xb)
    # 梯度
    grads = autograd.grad(outputs=output_r, inputs=xr,
                          grad_outputs=torch.ones_like(output_r),
                          create_graph=True, retain_graph=True, only_inputs=True)[0]
    # loss_r为Ritz变分格式、loss_b为边界处理、loss为损失函数
    loss_r = 0.5 * torch.sum(torch.pow(grads, 2), dim=1) - output_r
    loss_r = torch.mean(loss_r)
    loss_b = torch.mean(torch.pow(output_b, 2))
    loss = loss_r + 500 * loss_b
    Loss_list.append(loss / (len(xr) + len(xb)))
    optimizer.zero_grad()  # 优化器参数归零
    loss.backward()  # 误差反向传播
    optimizer.step()  # 神经网络参数（权重及偏置）更新
    torch.save(model.state_dict(), 'new_best_Deep_Ritz.mdl')  # 保存神经网络模型
    if epoch % 100 == 0:
        print('epoch:', epoch, 'loss:', loss.item(), 'loss_r:', (loss_r).item(), 'loss_b:',
              (500 * loss_b).item())
        if epoch > int(4 * epochs / 5):
            if torch.abs(loss) < best_loss:
                best_loss = torch.abs(loss).item()
                best_epoch = epoch
                torch.save(model.state_dict(), 'new_best_Deep_Ritz.mdl')
    # 连续绘图
    if epoch % 500 == 0:
        plt.ion()  # 打开交互模式
        plt.close('all')
        model.load_state_dict(torch.load('new_best_Deep_Ritz.mdl'))
        with torch.no_grad():
            x1 = torch.linspace(-1, 1, 1001)
            x2 = torch.linspace(-1, 1, 1001)
            X, Y = torch.meshgrid(x1, x2)
            Z = torch.cat((Y.flatten()[:, None], Y.T.flatten()[:, None]), dim=1)
            Z = Z.to(device)
            pred = model(Z)

        plt.figure()
        pred = pred.cpu().numpy()
        pred = pred.reshape(1001, 1001)
        ax = plt.subplot(1, 1, 1)
        h = plt.imshow(pred, interpolation='nearest', cmap='rainbow',
                       extent=[-1, 1, -1, 1],
                       origin='lower', aspect='auto')

        plt.title("Training times:" + str(epoch))
        divider = make_axes_locatable(ax)
        cax = divider.append_axes("right", size="5%", pad=0.05)
        plt.colorbar(h, cax=cax)
        plt.savefig('./Training_process/Deep_Ritz_' + str(epoch) + '.png')
        if epoch == best_epoch:
            plt.savefig('Best_Deep_Ritz.png')
        # plt.show()
        # plt.pause(0.02)

print('=' * 55)
print('学习结束'.center(55))
print('-' * 55)
print('最优学习批次:', best_epoch, '最优误差:', best_loss)
plt.close('all')
plt.ioff()  # 关闭交互模式
plt.title('Error curve')
plt.xlabel('loss vs. epoches')
plt.ylabel('loss')
plt.plot(range(0, epochs + 1), Loss_list, label='Loss')
plt.savefig('Error_curve_Deep_Ritz.png')
# plt.show()
print('已生成"最优拟合结果图"，请打开文件"Best_Deep_Ritz.png"查看')
print('已生成"误差曲线图"，请打开文件"Error_curve_Deep_Ritz.png"查看')
print('-' * 55)
print('准备绘制训练过程动态图')
image2gif.image2gif('Deep_Ritz')
print('=' * 55)

Open your Python!

Python

参考书籍及文献

  1. 李航.《统计学习方法》.清华大学出版社.
  2. 周志华.《机器学习》.清华大学出版社.
  3. 诸葛越.《百面机器学习算法工程师带你去面试》.人民邮电出版社
  4. (英) 塔里克 - 拉希德.《Python神经网络编程》.人民邮电出版社
  5. Physics Informed Deep Learning (Part I)
  6. Physics Informed Deep Learning (Part II)
  7. DeepXDE- A Deep Learning Library for Solving Differential Equations
  8. 文献解读-Physics Informed Deep Learning(PINN)
  9. 文献解读-物理信息深度学习(PINN)

若有侵权,请联系作者删除

由于本人水平有限，如有理解或描述错误，还请各位批评指正.

作者邮箱: 517093978@qq.com

机器学习大作业《Kaggle赛题之Kannada MNIST研究》论文和Python代码
业精于勤，荒于嬉
05-19 2265
一、赛题概述及分析 1、背景介绍 邮政系统每天都会处理大量的信件，最为要紧的一环是要根据信件上的收信人邮编进行识别和分类，以便确定信件的投送地。原本这项任务是依靠大量的人工来进行，后来人们尝试让计算机来替代人工。然而，因为多数的邮编都是手写的数字，并且样式各异，所以没有统一编制的规则可以很好地用于识别和分类。 20世纪80年代，美国国家标准与技术研究所（National Institute of Standards and Technology，即NIST）建立了经典的MNIST数据集，该数据集由250个不
自然语言处理NLP课程不会选择？这篇测评或许可以解你困惑
weixin_48649532的博客
07-23 455
引言 自然语言处理(Natural Language Processing, NLP)是计算机科学领域与人工智能领域中的一个重要方向。它研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法。自然语言处理是一门融语言学、计算机科学、数学于一体的科学。 学过NLP的都知道，学习一些基础知识和调用一些NLP的库，最后用到项目中发现效果并不好，需要你优化或者修改的时候就开始懵逼了。这是很多初学者有的一个疑问，最后决定去学习提升一下，但是目前市场上的课程杂又多，我们该如何选择一门适合自己的课程呢？ 我们如何
机器学习期末总结
qq_46618854的博客
01-04 1218
机器学习 三要素：数据，模型，策略； 计算机利用已有的数 据(经验)，得出了某种模型，并利用此模型预测未来的一种方法。 分类 监督学习 指从标注数据中学习预测模型的机器学习问题。标注数据表示输入输出的对应关系，预测模型对给定的输入产生相应的输出。监督学习的本质是学习输入到输出的映射的统计规律。 无监督学习 指从无标注数据中学习预测模型的机器学习问题。无标注数据是自然得到的数据，预测模型表示数据的类别，转换或概率。无监督学习的本质是学习数据中的统计规律或潜在结构。 聚类，降维，关联规则，推荐系统。 强化学习
机器学习评测指标概述
当赤道留住雪花
05-07 880
机器学习评测指标概述 文章目录机器学习评测指标概述1. 基本分类1.1 样本类别1.2 置信度阈值1.3 IoU阈值2. 基本指标recallprecisonaccuracy3.进阶指标3.1 F1-score3.2 pr曲线定义计算方式计算函数目标检测的pr曲线计算多分类p-r曲线计算方式3.3 mAP定义求解方式计算函数3.4 混淆矩阵定义计算函数参考文献 1. 基本分类 1.1 样本类别 机器学习评测任务的一个样本，根据预测结果和标注结果的不同，有如下所示的四个类别： 真实\预测 正类 负类
机器学习测试一总结
厄尔尼诺的博客
07-22 322
1、神经网络中权值绝对值尽可能小的原因是什么？为什么不直接设置为0？ 2、CNN（卷积神经网络）中梯度梯度不稳定是指什么？梯度消失的原因是什么？如何防止这种情况的出现？ 3、损失函数中采用交叉熵而不是均方差的原因是什么？ 4、BP反向传播的一些特点 5、监督学习、无监督学习 6、KNN、K—means 一、 关于神经网络中超参数初始化问题，详细请参考这篇博客 二、不稳定是指：梯度消失跟梯度爆炸...
人工智能考核（机器学习）
ldq_learning的博客
09-26 499
1、请简要介绍下SVM？ 答:支持向量机（SVM）是用来解决分类问题的学习模型，也称“最大间隔分类器”。把低维不可分拉伸到高维可分，所以会用到核函数，如:高斯核函数，卡方核函数，字符串核函数与直方图核函数。 使用范围：当使用核函数时，对于高维稀疏，并且样本较少的案例比较适用。 当不使用核函数时，也就是线性喽，速度快，效果也很不错。 2、简要介绍下tensorflow的计算图？ 答:在tensorf...
综述论文：机器学习中的模型评价、模型选择与算法选择！
小白学视觉
04-29 1244
点击上方“小白学视觉”，选择加"星标"或“置顶”重磅干货，第一时间送达选自 Sebastian Raschka，来源：机器之心本论文回顾了用于解决模型评估、模型选择和算法选择三项任务的不同技术，并参考理论和实证研究讨论了每一项技术的主要优势和劣势。进而，给出建议以促进机器学习研究与应用方面的最佳实践。论文链接：https://sebastianraschka.com/pdf/manuscripts...
使用机器学习技术预测糖尿病-研究论文
06-10
在本研究中，使用了六种流行的机器学习技术，即随机森林 (RF)、逻辑回归 (LR)、朴素贝叶斯 (NB)、C4.5 决策树 (DT)、K-最近邻 (KNN) 和支持向量比较机器 (SVM) 以获得出色的机器学习技术来预测糖尿病。 我们的新...
大学生综合测评管理系统.zip
09-15
此外，系统可能还会运用到数据挖掘、机器学习等技术，以提高数据分析的精准度和智能化程度。 三、系统应用价值 1. 提高工作效率：系统自动化处理大量测评数据，减轻了人工计算和统计的工作量，提高了工作效率。 2...
基于深度学习对修订版布卢姆分类法的终结性评估分类研究
最新发布
03-26
内容概要：本文研究了利用卷积神经网络（CNN）和长短期记忆网络（LSTM）这两种深度学习技术，针对修订版布卢姆分类法对软件工程课程的期末考试题进行分类。研究提出了一个模型，旨在通过自动识别认知过程与知识维度...
期末复习--机器学习总结（全）
Zsusan7的博客
12-20 5134
数据挖掘的定义？ 数据挖掘是指从大量的、随机的、不完全的、有噪声的、模糊的应用数据中，提取出潜在有价值的信息，该过程自动完成，信息的表现形式可以为规则、概念、模型、模式等。 知识发现的过程？ 确定知识发现的目标 数据采集 数据探索 数据预处理 数据挖掘 模式评估 数据挖掘任务主要集中在哪些方面（也叫数据挖掘的模式类型）？哪些是预测性任务，哪些是描述性任务？ 主要集中在回归、分类、预测、关联、聚类、异常检测6个方面，前3个是预测性，后3个是描述性 pandas两种核心数据结构 一维数据结构Series，二
机器学习期末复习总结笔记（李航统计学习方法）
半岛铁盒里
01-23 2031
机器学习（李航统计学习方法）期末总结复习
机器学习组考核分析
weixin_52356220的博客
09-11 322
1. 当数据有缺失值的时候， 你认为处理缺失值比较合理的方法(缺失值举例：泰坦尼克号幸存者数据中 有年龄 性别 职业 是否存活 四个特征 但某些样本的职业特征为空)。 (1)均值，极值，众数，中位数填补 (2)回归决策树预测，把label作为特征也加入到特征里来 3.如果缺失值占样本比例比较小的话也可以直接将缺失值删掉 2. 请简述随机梯度下降，批梯度下降的区别和各自的优点 (1) 随机就是计算一个样本的loss之后就进行梯度下降 a) 优点：迭代速度快，可以跳出局部最小(因为震荡大) b) 缺
【机器学习】【期末复习】有关机器学习的计算题可供期末复习参考（带本人手写解答与思考）
热门推荐
网瘾中心呼唤爱的博客
06-26 1万+
本文为学校课程《机器学习》的期末复习材料，主要是关于一些机器学习模型的计算题的解答过程。
机器学习测试、期末考试题（部分）
qq_62913618的博客
06-19 1762
答案解析：def compute_cost(x, y, w, b): m = x.shape[0] cost_sum = 0 for i in range(m): f_wb = w * x[i] + b cost = (f_wb - y[i]) ** 2 cost_sum = cost_sum + cost total_cost = (1 / (2 * m)) * cost_sum。逻辑回归的输入是线性回归的输出；
机器学习期末考试题库【最全考试题库】
qq_62660798的博客
01-25 7364
本文有特别详细的机器学习这门课期末考试会考到的相关的概念，并配有相关的习题，大家把这一块学明白了，考试可以有很大的助力，喜欢的朋友点一下关注吧，持续关注我，我会后面陆续更新更多的资源哟~（づ￣3￣）づ╭❤～
终于有人把机器学习中的评价指标讲清楚了
Grace_yan的博客
10-14 636
终于有人把机器学习中的评价指标讲清楚了 https://mp.weixin.qq.com/s/EZw12p5qu_yYbyHfA55sgQ 训练与识别 正例与负例 混淆矩阵，这个没有说清楚 模型性能指标 正确率（Accuracy） 错误率（Error-rate） 精度（Precision） 召回率（Recall） 精度-召回率曲线（PR曲线） AP（Average Precision）值 mAP（...
机器学习系列笔记(1)——统计机器学习基础
Ray的博客
12-11 442
统计学习概论 损失函数是指：针对单个具体样本，表示模型预测值与真实样本值之间的差距。损失函数越小，说明模型对于给样本预测越准确。常见损失函数有0-1损失函数、平方损失函数、绝对损失函数以及对数损失函数。 经验风险：对所有训练样本都求一次损失函数，再累加求平均。即，模型f(x)f(x)f(x)对训练样本中所有样本的预测能力。 Remp(f)=1N∑i=1NL(yi,f(xi))R_{emp}(f)...
学堂在线_大数据机器学习_小笔记
.
06-12 700
学堂在线大数据机器学习小笔记20220607 - https://www.xuetangx.com/learn/THU08091001026/THU08091001026/10333105/video/17653559-----------------第2章_机器学习基本概念 - 假设空间：模型函数的集合。 - 训练集越小、且模型函数越复杂时，就越容易 过拟合（测试集的损失太多（泛化误差太大））。 减小泛化误差的方法：（1）增加训练集数据量，训练集变大；（2）模型正则化，给模型函数添加 正则化项（即 罚项，
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

图灵猫

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值