浅谈电磁学——高斯定理环路定理

最新推荐文章于 2023-09-03 18:38:42 发布

IamOrthoPole

最新推荐文章于 2023-09-03 18:38:42 发布

阅读量2.3k

点赞数

分类专栏：电磁学文章标签：电磁学物理学

本文链接：https://blog.csdn.net/qq_42876636/article/details/104102192

版权

本文深入浅出地探讨了电磁学中的高斯定理和环路定理。首先介绍了电场线的概念及其意义，接着详细阐述了电通量的定义，并通过证明高斯定理展示其在静电场中的应用，如求解均匀带电球壳和球体的电场分布。此外，还解释了环路定理，说明静电场中不存在闭合电场线。最后讨论了电场线的疏密与电场强度的关系。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

系列文章：
浅谈电磁学——基本电现象
 浅谈电磁学——电场
 浅谈电磁学——高斯定理环路定理

一、电场线

为了形象地描述电场，人们引入了电场线的概念。

电场线是在电场中的曲线，它的切线处处平行于场强。

也就是说，电场线可以用来描述电场方向。

需要注意的是，电场线并不实际存在，是人为规定的。

以下是常见的一些电场线：
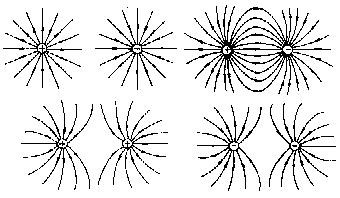
常见的电场线
第一行最后一幅图就是电偶极子产生的电场。

二、电通量

电场是矢量场，和流速场、重力场是相似的。既然流速场中有流量，那么电场中也应该有电通量。

电场虽然没有东西在流动，但是仍能够定义电通量。

设微小曲面 ${\rm d}S$ ，法向量为 $\bm n$ ，场强为 $\bm E$ ， $\bm E$ 与 $\bm n$ 的夹角为 $\theta$ ，则电通量 ${\rm d}\varPhi_\bm E$ 定义为 ${\rm d}\varPhi_\bm E=E{\rm d}S\cos\theta=\bm E\bullet\bm n{\rm d}S$ 如果定义面元 ${\rm d}\bm S=\bm n{\rm d}S$ ，那么 ${\rm d}\varPhi_\bm E=\bm E\bullet{\rm d}\bm S$ 。对于曲面 $S$ ，电通量为 $\varPhi_\bm E=\iint_S{\bm E\bullet{\rm d}\bm S}$

三、高斯定理

在静电场中，任何一闭合曲面的电通量等于其包含的电荷量的 $1/\varepsilon_0$ 倍。

这一定理被称作高斯定理。下面证明这个定理。

考虑只有一个点电荷 $q$ 的情形。
$\varPhi_\bm E=\oiint_S{\bm E\bullet{\rm d}\bm S}=\oiint_S{\frac1{4\pi\varepsilon_0}\frac{q{\rm d}S\cos\theta}{r^2}}=\frac q{4\pi\varepsilon_0}\oiint_S{\frac{ {\rm d}S\cos\theta}{r^2}}$