AI(人工智能:一种现代的方法)学习之: 对抗搜索（adversarial search）Minimax / alpha-beta pruning

博弈类型

零和博弈 zero-Sum Games

• 进行博弈的多个 agent 之间采用的 utility （values on outcomes） 是相对的，即如果当前的 agent 的 utility 是正值，那么对方就一定是负值，我们把这种博弈的状态叫做 pure competition 或者 adversarial

普通博弈 general Games

• agents 各自拥有独立的 utilities （value on outcomes）

• 存在合作、双赢、竞争等多种可能性

• 其实生活中的大多数场景都是 普通的博弈场景，但是这种场景也大都可以简化成零和博弈的场景。

• 零和博弈其实是一种理想情况，那就是假设对方的行为和当前的 agent 是纯竞争，彼此都想让对方的收益最小，自己的收益最大。

非博弈的情况

• 如果只有一个 agent，现在处在这棵搜索树边缘上的值分别是 8（第三层），2,0,2,6,4,6 （处在最后一层）：

• 因为只有一个agent ，这个时候 agent 希望自己获得的收益最大，那么只要递归地将当前节点的值等于children 节点的最大值就可以了。
  
  • 因此通过一层层地向回传递，最终可以得到 agent 可以得到的最大收益是 8
  • 整个过程中依据的公式是：
    $$V(s)=\underset{s^{{}^{\prime }}\in children(s)}{\max }V(s^{{}^{\prime }})$$
  • 就是总是从 children 里面挑选拥有最大值的节点

博弈情况（博弈树）

• 现在是有两个 agent 了，这两个 agent 进行完全的博弈，即对方都希望自己收益最大，并且敌方收益最小：

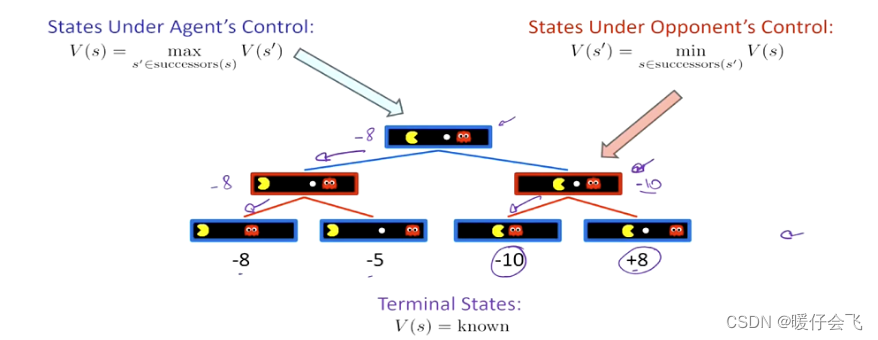
• 在当前的情况中，假设一个 agent 是吃豆人 $Y$，一个是红色的小鬼$R$，边缘（叶子结点）上所有的值如下图所示，在这种情况下，吃豆人想得到最大的收益可就没有那么简单了，因为 $R$ 总会最小化当前步骤的 $Y$ 的收益。

• $R$ 实际上掌控着下图的两个节点，因此在 $R$ 的掌控范围内，对 $Y$ 来说应该是返回最小的值 ：
  
• 所以对于 $Y$ 来说，它在 子节点 拿到的只能是 $R$ 经过严格把关后的最小值，所以应该是下面的情况：
  
• 所以作为 $Y$ 只能从 { − 8 , − 10 } \{-8,-10\} {−8,−10} 中选一个最大的，因为这就是当前在博弈的情况下 $Y$ 能够选的所有的值；所以最后 $Y$ 会选择 $-8$ 也就是说，$Y$ 最终会选择左侧的分支并且到达最终值为 $-8$ 的叶子节点状态。
• 因此用数学的形式化表示为：
  
  $$V(s)=\underset{s^{{}^{\prime }}\in successors(s)}{\max }V(s^{{}^{\prime }}),$$
  $$V(s^{{}^{\prime }})=\underset{s\in successors(s^{{}^{\prime }})}{\min }V(s)$$

• 从上面的例子可以看出，博弈搜索的时候，面对所有的值，哪怕有更好的也不一定能得到，因为还要考虑对方做出的行为。
  

最大最小算法

• 最大最小算法 top-down 的，首先由一个 root 节点开始向下遍历，直到叶子节点（terminal state）然后进行返回，返回的值会保持在它的父节点中，直到父节点遍历完了其所有的叶子节点，然后父节点会判断自己处于 MIN 层还是 MAX 层，如果是 MIN 层，那么要选择最小的值作为其结果，并向其上一层返回。

• 这本质上类似于一个深度优先遍历，会从一边一直遍历到 terminal state 然后返回
• 例如在 terminal state 的节点有三个值，3,12,8 这三个值都向上返回保存在父节点中，这里暂且用 $p$ 表示，而 $p$ 当前是一个 MIN 层，所以会选择最小的 $3$，并返回到根节点 root；root 现在有一个可选的值：3
• 接下来是同样的操作对第二个分支；当 2,4,6 将值返回到父节点，父节点处在 MIN 层，因此会选择最小的值 2， 然后将 2 返回到 root 节点，现在 root 节点有两个可选的值：{2,3} 由于root 节点是一个 MAX 层，因此它会保留 3 作为 root 的选择
  
• 然后是第三个分支：
  
• 经过第三个分支返回到 root 的值是 2，因此 root 依然保留当前的选择：3；所以最后 root 选择的值是 3；所以最终这个 agent 选择的行为是：
  

博弈树剪枝（game tree pruning）

• 在 CSP 的问题中，我们通过前向检查或者是弧相容来将一些可能出错的方式暴露出来，从而提前进行回溯，在这里也是采用相似的策略，即对于一些注定不可采用的分支，我们越早修剪掉，后面造成的计算浪费就越少。

• 在这个例子中，通过最左边的树我们可以知道在 MAX 层的一个可选值是 3，也就是说 MAX 最终做的决定一定是 $>=3$，因此当 MIN 层返回上来的值是 $<3$ 的，那么这个MIN 层的节点就没有继续探索的必要了
• 基于这个理论，我们看中间的这个分支，中间分支在遍历第一个叶子节点（值=2） 时，我们就知道根据 MIN 层的规则，MIN 最终选出的值的范围一定是 $<=2$ 的，因此它不符合继续 MAX 层的最低要求；所以当前这个 MIN 层的中间节点就没有必要再去遍历其他的子节点了。
  
• 然后继续遍历最右边分支的叶子节点，当遍历右边的第一个叶子结点之后，得到 MIN 层最右边的节点的值范围是 $<=14$
  
• 继续遍历右边的叶子结点，然后 MIN 层最右边的叶子结点值范围更新为 $<=5$:
  
• 同样的，再次遍历右边的叶子结点，将 MIN层最右边的节点值范围更新为 $<=2$，因为 MIN 层最右侧的节点的叶子结点全部遍历完成，因此最终决定了 MIN 层最右端的结点最终结果是 2；并回传到 MAX 层的节点；最终还是选择 3 这个选择：
  

Alpha-Beta Pruning（alpha-beta 剪枝）

• 处于 MIN 层的结点的值只可能不断缩小，不可能增大，而 MAX 层的结点的值只可能增大
• 针对一棵博弈树，假设有一个 MIN 层的结点 $mi$ ，它有 $n$ 个 children 节点，而且当前 MIN 的值的范围是 $value<=x$；当前 MAX 层的结点 $ma$ 最小值是 $\alpha$；
• 在这种情况下，如果 $mi$ 在搜索 $n$ 个子节点的过程中发现有一个节点导致 $x<\alpha$ 那么 $ma$ 就会忽略当前这个 $mi$ 剩下的所有子节点。

• 通过这个算法再来演示一下上面的过程：
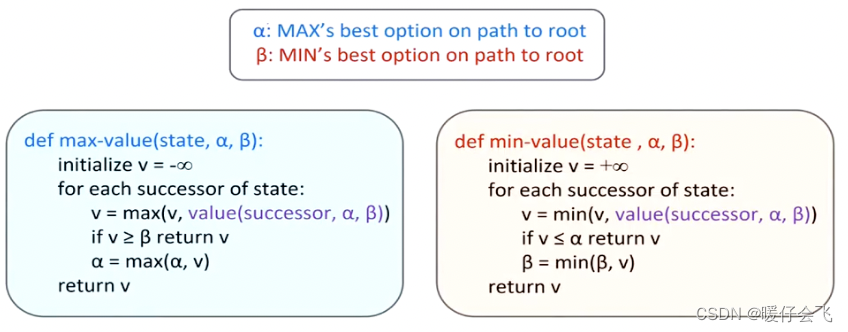
  • 首先对于 MIN 层的操作，对 MIN 进行操作的时候调用的是 min_value 这个函数，传进来的 $\alpha$ 值的作用就是比较当前 MIN 层的节点是否出现了比 $\alpha$ 更小的值，如果出现了（$v\le \alpha$）就可以直接返回，代表对这个节点后面的探索情况不关心了，因为已经没有搜索的价值了。而 $\beta$ 代表的是当前 MIN 层中的节点 $mi$ 当前采用的最小值，因此如果遇到了更小的值当然应该更新。
  • 对于 MAX 层的操作，因为它选用的值只会扩大不会减小，因此我们需要根据子节点返回的值不断更新 $\alpha$，而如果当 $v$ 的值大于 MIN 层当前可选的最小值的时候，就直接返回 $v$ 而对这个 MAX 层节点 $ma$ 后面的子节点不予关心。
• 无论是对 MAX 还是 MIN 层的节点进行操作，$\alpha ,\beta$ 的值都是从上向下传递的，而 return 的时候都只返回一个 $v$ 给上一层节点。
• 总结一下，MIN 层的节点值只会越更新越小，MAX 层的节点值只会越更新越大，因此当前如果是 MIN 层，那么如果出现了比它的上一层的 MAX 中的最大值更小的值，那么这个 MIN 层的节点就失去了继续探索的价值；同理如果当前是 MAX 层的节点，并且当前节点的值出现了比它的上一层的 MIN 中的节点的最小值更大的值，那么这个 MAX 层的节点也就失去了继续探索的意义。

• 看一个具体例子的更新过程来更加深入了解 alpha-beta pruning

• 所有向上的三角表示的是处于 MAX 层的结点，而向下的三角表示的是处于 MIN 层的结点
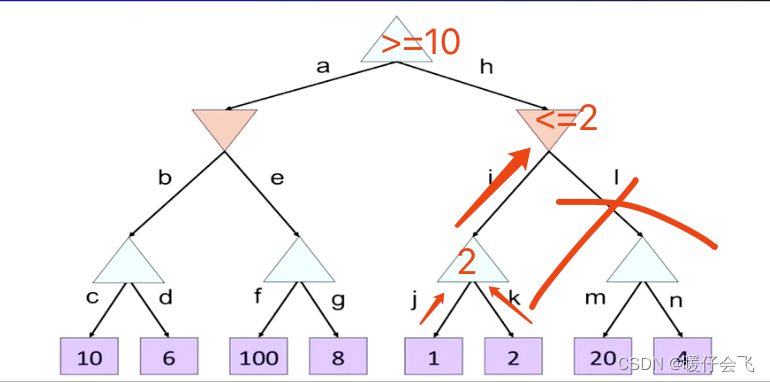
  > - 根据第一个叶子节点更新 MAX 层的值域为 $\ge 10$；然后遍历第二个叶子结点；MAX 层的节点的值域更新为 $\ge 6$ 所以最终将 $10$ 返回到上一层的 MIN 结点并更新 MIN 节点的值域为 $\le 10$
  
• 继续从 e 向下遍历子节点，通过 f 分支的叶子结点更新 MAX 的值域为 $\ge 100$，而上面的 MIN 约束是 <=10，因此再往后遍历也没意义了，所以就不遍历 g 了：
  
  然后将 100 的值传回上一层的 MIN，但并不会改变 MIN 当前 $\le 10$ 的现状
• 然后 MIN 节点的值确定了是 $10$，并将这个值传回到最上层的 MAX；最上层的 MAX 的值域更新为 $\ge 10$
  
• 然后开始遍历右边的子树：
• 遍历 j ，MAX 更新值域 $\ge 1$，遍历 k，更新 MAX 值域 $\ge 2$，然后更新 MAX 层的值为 $2$，将 $2$ 传递到 MIN 层节点，更新 MIN 结点值域为 $\le 2$；由于与最上层的 MAX 结点范围发生冲突，直接忽略 I 及以后分支
  

• 因此这个 MAX 的上一个 MIN 层的最小值