1、整数规划的分支定界法:
- 分支定界法的基本步骤:比如给出整数规划方程
,先利用单纯形法求出解看看是不是恰好为整数解,如果是那就是整数规划的最优解;如果不是则进入下面的过程:
- 解得
;明显这个最优值
是所需要值的下界(整数最优解肯定是要比这个值大一点),故将其令为
;由于两个变量的取值都不是整数,故任取一个进行“分支”;首先,我们将
分成两个最靠近的
进行考虑;
- 先考虑
的情况:即求解
这个线性规划方程,得到
,考虑到解里仍然有非整数,这里需要将
进行分支,分为
;
- 先考虑
的情况:即求解
这个线性规划方程,得到无解;
- 再考虑
的情况:即求解
这个线性规划方程,得到
;发现恰好是整数解,故无需分支,直接将其确定为最优解的上界,记作
;
- 先考虑
- 然后再考虑
的情况:即求解
这个线性规划方程,得到无解;
- 先考虑
- 综上所述,所有可能分支均已讨论完毕,因此原问题的最优解和最优值分别为
;
- 解得
- 分支定界法的注意事项:
- 一个分支被查清的标志是下面各条之一:
- 忽略整数约束后的线性规划无解;
- 忽略整数约束后的线性规划的最优解是整数解;
- 忽略整数约束后的线性规划的最优值超过原问题最优值的上界,这说明原问题的最优解肯定不在这一分支;
- 整个问题解完的标志是下面各条之一:
- 各分支均已查清,则所得整数解中最好者为最优解;
- 某分支中,得到整数解且相应目标函数值等于原问题最优值之下界,则该整数解即为原问题的最优解;
- 分支定界法也适用于混合整数规划,对于没有整数约束的变量不必进行分支,这会大大减少分支的数量;
- 一个分支被查清的标志是下面各条之一:
2、0-1规划的隐枚举法:
- 0-1规划的基本思路:设0-1规划的变量个数为
, 由于每个变量仅取0或1,因此,所有可能组合解为
个;检查每一组合解,通过比较目标函数值大小而求得最优解的方法称为全枚举法(显枚举法);当
较大时,全枚举法的计算量骤增;
- 隐枚举法的基本思路:只检查一部分变量组合, 在此过程中根据已有信息自动放弃一系列不可能成为最优解的组合而求得最优解;具体操作是:将所有变量的可能组合解按一定次序(如字典序)排列起来,依次检查是否为可行解;
- 若为可行解,则计算其目标函数值(若下面要检查的点的目标函数值不优于它,则排除此点),比较所有可行点的函数值,给出最优解和最优值;
- 若有一个约束条件不满足,则不是可行解,可排除此点;
- 隐枚举法的基本步骤:
- 已知0-1规划方程
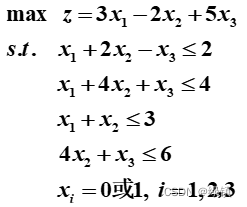 ,发现有三个变量共8个可能的组合解,列表如下:
,发现有三个变量共8个可能的组合解,列表如下: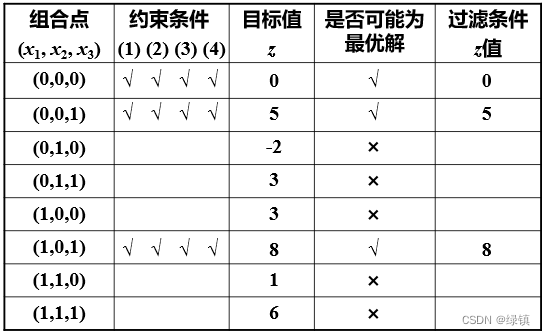 ;
; -
由此表得最优解为
,最优值为8;
- 已知0-1规划方程
- 更优化的隐枚举法:
- 对于目标函数求最大值的0-1规划:
- 作变量替换,将目标函数中变量的系数全部变为非负数;
- 将变量重新排序,使目标函数中变量的系数从大到小排列;
- 将所有新变量的一切可能组合解按照从大到小的顺序(字典序)排列,依次检查各点的可行性,第一个可行点即为最优解;
- 对于目标函数求最小值的0-1规划:
- 作变量替换,将目标函数中变量的系数全部变为非负数;
- 将变量重新排序,使目标函数中变量的系数从大到小排列;
- 将所有新变量的一切可能组合解按照从小到大的顺序(字典序)排列,依次检查各点的可行性,第一个可行点即为最优解;
- 对于目标函数求最大值的0-1规划:
- 更优化的隐枚举法的基本步骤:
- 已知0-1规划方程
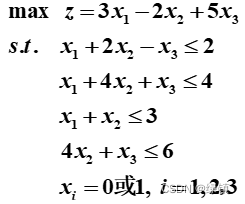 ,先令
,先令,这样就可以把方程变为:
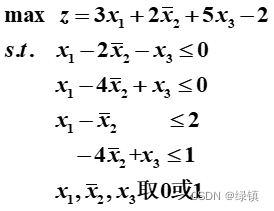 ;
; - 然后我们按照变量系数从大到小进行排列,得到:
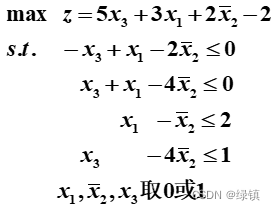 ;这样所有新变量的组合解为
;这样所有新变量的组合解为;检查8种可能性后发现只有
满足,那么最后原问题的最优解为
;最优值为
;
- 已知0-1规划方程
3、整数规划模型建立举例:
- 一项说明书要由汉语分别译成英、日、德、俄四种文字,交由甲、乙、丙、丁4个译员去完成。因各人专业不同,因此译成不同文字所需要的时间不同。假设各人完成各项工作的时间如下表,问应如何分配才能完成4项给定任务的总时间最少?
| 工作序号 | 1 | 2 | 3 | 4 | |
| 译员 | 工作名称 | 汉译英 | 汉译日 | 汉译德 | 汉译俄 |
| 甲 | 3 | 10 | 9 | 7 | |
| 乙 | 15 | 4 | 14 | 8 | |
| 丙 | 13 | 14 | 16 | 11 | |
| 丁 | 4 | 15 | 13 | 9 | |
- 考虑到译员面对这些工作可以选择做或者是不做,设0-1变量
为第
名译员是否承担第
项任务:
 ,其中
,其中,
为第
名译员承担第
项任务的工时;
- 以下则是约束条件:
- 第
项任务有且仅有一名译员完成:
;
- 第
名译员完成且仅完成一项任务:
;
- 目标函数,任务总工时:
;
- 第
- 那么该指派问题的整数规划模型为:
;
4、网络优化:
- 图与网络的基本概念:
- 图:由一组点,与点之间的连线/边所组成的总体;
- 网络:各条边上赋有权数的图;
- 路径:网络中一个前后相继并且方向相同的边序列
,像下图里如:
;
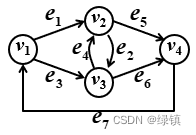
- 链:网络中一个前后相继但方向不一定相同的边序列
,像上图里如:
;
- 回路:闭合的路径,像上图里如:
;
- 圈:闭合的链;
- 连通图:任何两个节点之间都有一条链的网络;
- 树:无圈的连通图;
-
从集合的角度看,图
是由一个节点集
和一个边界
组成, 可以表示为
;在上图中,
;
-
无向图的矩阵表示:
-
关联矩阵:表示图
中顶点与边的联接关系的矩阵,记为
,其中
 ;图
;图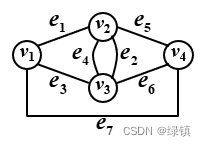 中的关联矩阵
中的关联矩阵为:
 ;
; -
邻接矩阵:表示图
的顶点之间的邻接关系的矩阵,记为
,其中
 ; 图
; 图 中的邻接矩阵
中的邻接矩阵为:
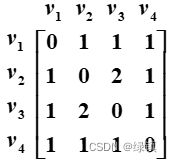 ;
;
-
-
有向图的矩阵表示:
-
关联矩阵:表示图
中顶点与边的联接关系的矩阵,记为
,其中
 ; 图
; 图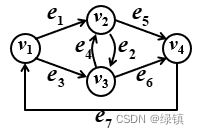 中的关联矩阵
中的关联矩阵为:
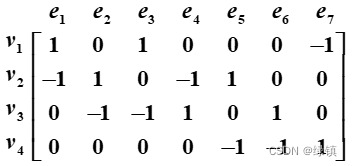 ;
; -
邻接矩阵:表示图
的顶点之间的邻接关系的矩阵,记为
,其中
为以
为起点和以
为终点的边数; 图
 中的邻接矩阵
中的邻接矩阵为:
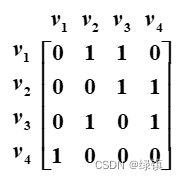 ;
;
-
- 最短路径问题举例:
- 最短路径的性质:若
是
至
的最短路径, 则
是
至
的最短路径;
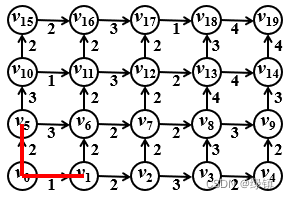
- 下图是各城市之间的交通网,求
至其它各点的最短路径:这里采用迪克斯特拉(Dijkstra)算法:
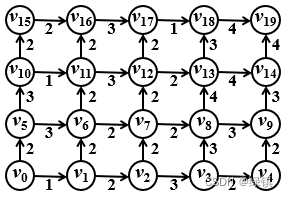
- 与
邻接的点有
,显然与
的距离近,取
;连接
, 令顶点集
;
- 然后发现与顶点集
邻接的点有
,且
;其中
,故连接
,进一步令
;这两步下来得到的图形如下:
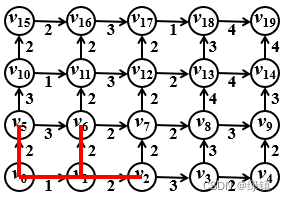
- 接着发现与顶点集
邻接的点有
,且
;其中
,连接
,进一步令
;这三步下来得到的图形如下:
- 按照这样的步骤进行下去,我们最终可以得到:
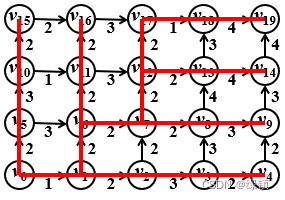
- 与
- 最短路径的性质:若
- 网络流问题/最大流问题:从一个地点输送尽可能多的物资至另一地点,具体例子如下:
- 图1
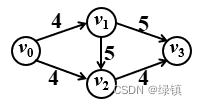 表示运输网络图,权数为该路的最大通过量/容量,求由
表示运输网络图,权数为该路的最大通过量/容量,求由至
的最大流;
- 这里采用逐步扩大法,先任作一可行的运输方案,并将运输量/流量标于图上,如图2:
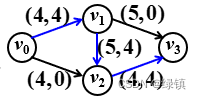 ;
; -
通过画“增广图”检查现有方案基础上能否增加运量:若否,则此方案为最大流方案;若能,修改方案,继续讨论,直到得到最大流方案为止;增广图的画法如下:
-
已分配有流量的边,均画一反向边,反向边的容量为现有方案中分配的流量数;
-
分配的流量小于容量的边照常(方向)画,但新容量改为旧容量与流量的差;
-
-
依照画增广图我们得到图3
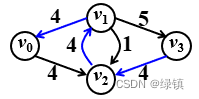 ,在该图上我们还可以找到
,在该图上我们还可以找到至
的通路,如图4所示
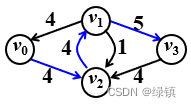 ;即流量还可扩充,于是考虑继续修改方案,得到图5:
;即流量还可扩充,于是考虑继续修改方案,得到图5: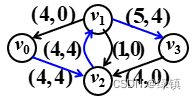 ;
; -
将图4
 中通路的流量“叠加”在图2
中通路的流量“叠加”在图2 上,得到图6:
上,得到图6: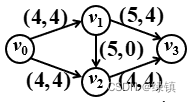 ;
; -
再作增广图(图7):
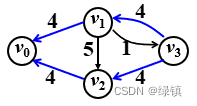 ;发现已没有
;发现已没有至
的通路,则图6
 所示的方案为最大流方案。
所示的方案为最大流方案。
- 这里采用逐步扩大法,先任作一可行的运输方案,并将运输量/流量标于图上,如图2:
- 图1






















 1180
1180











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








