KKT条件与SVM

《最优化理论》课程作业

1. SVM介绍

支持向量机SVM是一种二分类模型，其基本模型是定义在特征空间上的间隔最大的线性分类器。

设有数据集 T { ( x i , y i ) ∣ i = 1 , . . . , N } T \left \{ (x_i,y_i)|i=1,...,N \right \} T{(xi​,yi​)∣i=1,...,N}，$x_i$是第i个数据样本的特征，$x_i\in R^m$，即特征为m维，每个样本的标签类别 y i ∈ { − 1 , + 1 } y_i \in \{-1,+1\} yi​∈{−1,+1}，当$y_i=-1$时，称$x_i$为负例；当$y_i=+1$时，称$x_i$为正例。

假设数据T是线性可分的，即存在超平面S: $w^{T}x+b=0$能够将数据集T中的正实例和负实例点完全划分到超平面两侧，即对$y_i=+1$的正例，$w\cdot x_i+b>0$，对$y_i=-1$d的负例，$w\cdot x_i+b<0$。显然，这是一个二分类问题。

当数据集线性可分时，存在无穷多个分离超平面可以将两类数据正确分开。线性可分支持向量机通过（几何）间隔最大化或等价地求解相应的凸二次规划问题得到分离超平面。

2. SVM推导

2.1 函数间隔与几何间隔

超平面$(w,b)$关于某一样本点$(x_i,y_i)$的函数间隔定义为
$${\hat{\gamma }}_i=y_i\left(w\cdot x_i+b\right)$$超平面$(w,b)$关于所有样本点$(x_i,y_i)$的函数间隔定义为所有样本点函数间隔的最小值：
$$\hat{\gamma }=\underset{i=1,...,N}{\min }{\hat{\gamma }}_i$$对函数间隔进行规范化，则超平面$(w,b)$关于某一样本点$(x_i,y_i)$的几何间隔定义为
$${\gamma }_i=y_i\left(\frac{w\cdot x_i+b}{||w||}\right)$$几何间隔是实例点到超平面的带符号的距离（符号是因为$y_i$可正可负）。

超平面$(w,b)$关于所有样本点$(x_i,y_i)$的几何间隔定义为
$$\gamma =\underset{i=1,...,N}{\min }{\gamma }_i$$由上述定义，可以得出函数间隔与几何间隔间的关系：
KaTeX parse error: Unexpected end of input in a macro argument, expected '}' at position 55: …ad \gamma=\hat \̲f̲r̲a̲c̲ ̲{\gamma}{||w||}

SVM学习的基本思想是求解能够正确划分数据集并使几何间隔最大的超平面。虽然对线性可分的数据集而言，分离超平面有无穷多个，但使几何间隔最大的分离超平面是唯一的。

求几何间隔最大的分离超平面的问题，可以转换为约束最优化问题：
$$\begin{gathered} \underset{w,b}{\max }\gamma \\ s.t.y_i\left(\frac{w\cdot x_i+b}{||w||}\right)\ge \gamma ,i=1,2,...,N \end{gathered}$$即希望最大化超平面$(w,b)$关于数据集的几何间隔$\gamma$，并使超平面关于每个样本点的几何间隔至少是$\gamma$。
用函数间隔替换几何间隔，可将优问题改写为：
$$\begin{gathered} \underset{w,b}{\max }\frac{\hat{\gamma }}{||w||} \\ s.t.y_i\left(w\cdot x_i+b\right)\ge \hat{\gamma },i=1,2,...,N \end{gathered}$$函数间隔并不影响优化问题的解，故将$\hat{\gamma }$替换为1，又最大化$\frac{1}{||w||}$（另一个角度，最大化平面$wx+b=-1$与平面$wx+b=+1$的距离，即$\frac{2}{||w||}$）与最小化$\frac{1}{2}||w|{|}^2$是等价的，则得到SVM对应的优化问题的最终形式（原始最优化问题）：
$$\begin{gathered} \underset{w,b}{\min }f=\frac{1}{2}||w|{|}^2 \\ s.t.g_i=1-y_i(w\cdot x_i+b)\le 0,i=1,2,...,N \end{gathered}$$这是一个凸二次规划问题，并且没有等式约束，只有N个不等式约束。

2.2 解法一：对偶学习算法

引入拉格朗日乘子${\lambda }_i$,i=1,…,N ，构造广义拉格朗日函数：
$$L(w,b,\lambda )=\frac{1}{2}||w|{|}^2+\sum _{i=1}^N{\lambda }_i(1-y_i(w\cdot x_i+b))$$最终，将原始优化问题转化为极小极大问题：$$\begin{gathered} \underset{w,b}{\min }\underset{\lambda }{\max }L(w,b,\lambda ) \\ s.t.{\lambda }_i\ge 0 \end{gathered}$$其与上述原始最优化问题是等价的，因为当存在某个$g_i$不满足约束，即$g_i>0$时，$\underset{\lambda }{\max }L(w,b,\lambda )$将使${\lambda }_i\to +\infty$，此时$\underset{\lambda }{\max }L(w,b,\lambda )\to +\infty$；当所有$g_i$满足约束，即$g_i\le 0$时，$\underset{\lambda }{\max }L(w,b,\lambda )$将使${\lambda }_i\to 0$，此时$\underset{\lambda }{\max }L(w,b,\lambda )\to f$。

上述构造的广义拉格朗日函数是极小极大问题，其对偶问题，即极大极小问题：$$\begin{gathered} \underset{\lambda }{\max }\underset{w,b}{\min }L(w,b,\lambda ) \\ s.t.{\lambda }_i\ge 0 \end{gathered}$$

(1) 求$\underset{w,b}{\min }L(w,b,\lambda )$
拉格朗日函数关于$w,b$的偏导数等于0：
$$\begin{gathered} {\nabla }_{w}L(w,b,\lambda )=w-\sum _{i=1}^N{\lambda }_i{y}_i{x}_i=0 \\ {\nabla }_{b}L(w,b,\lambda )=\sum _{i=1}^N{\lambda }_i{y}_i=0 \end{gathered}$$将上述两式其代入拉格朗日函数：
$$L(w,b,\lambda )=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^N{\lambda }_i$$
第一阶段的结果$\underset{w,b}{\min }L(w,b,\lambda )=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^N{\lambda }_i$

(2) 求$\underset{\lambda }{\max }\underset{w,b}{\min }L(w,b,\lambda )$
$$\begin{array}{rl}& \underset{\lambda }{\max }-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^N{\lambda }_i\\ & s.t.\begin{array}{rl}& \sum _{i=1}^N{\lambda }_i{y}_i=0\\ & {\lambda }_i\ge 0,i=1,2,...,N\end{array}\end{array}$$其对偶问题为：
$$\begin{array}{rl}& \underset{\lambda }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^N{\lambda }_i\\ & s.t.\begin{array}{rl}& \sum _{i=1}^N{\lambda }_i{y}_i=0\\ & {\lambda }_i\ge 0,i=1,2,...,N\end{array}\end{array}$$记该最优解为${\lambda }^{\ast }={\lambda }_1^{\ast },{\lambda }_2^{\ast },...,{\lambda }_N^{\ast }$
有定理使该对偶问题与原始最优化问题满足：存在$a^{\ast },b^{\ast }$，使得$a^{\ast }$是原问题的解，$b^{\ast }$是对偶问题的解。这使得可以通过求解对偶问题间接求解原问题。

又有定理： 对凸规划问题，$a^{\ast }$、$b^{\ast }$分别是原问题和对偶问题的解的充要条件是该解满足KKT条件。
依此，满足KKT条件时，可以通过对偶问题的解$b^{\ast }$求得原问题的解$a^{\ast }$
当KKT条件成立时，有
$$\{\begin{array}{rl}& {\nabla }_{w}L(w^{\ast },b^{\ast },{\lambda }^{\ast })=w^{\ast }-\sum _{i=1}^N{\lambda }_i^{\ast }{y}_i{x}_i=0\\ & {\nabla }_{b}L(w^{\ast },b^{\ast },{\lambda }^{\ast })=\sum _{i=1}^N{\lambda }_i^{\ast }{y}_i=0\\ & {\lambda }_i^{\ast }(1-y_i(w^{\ast }\cdot x_i+b^{\ast }))=0,i=1,2,...,N\\ & 1-y_i(w^{\ast }\cdot x_i+b^{\ast })\le 0,i=1,2,...,N\\ & {\lambda }_i\ge 0\end{array}$$由此得
$$w^{\ast }=\sum _{i=1}^N{\lambda }_i^{\ast }{y}_i{x}_i$$由于至少有一个${\lambda }_j^{\ast }>0$，对此j，将上式$w^{\ast }$代入${\lambda }_i^{\ast }(1-y_i(w^{\ast }\cdot x_i+b^{\ast }))=0,i=j$，得
$$\begin{array}{rl}{b}^{\ast }& =\frac{1}{y_j}-w^{\ast }{x}_j\\ & =\frac{1}{y_j}-\sum _{i=1}^N{\lambda }_i^{\ast }{y}_i(x_i\cdot x_j)\\ & =y_j-\sum _{i=1}^N{\lambda }_i^{\ast }{y}_i(x_i\cdot x_j)(类别标签y_j的取值为\pm 1)\end{array}$$
至此，我们由对偶问题的解${\lambda }^{\ast }$求得了原始最优化问题的解
$$\{\begin{array}{rl}& w^{\ast }=\sum _{i=1}^N{\lambda }_i^{\ast }{y}_i{x}_i\\ & b^{\ast }=y_j-\sum _{i=1}^N{\lambda }_i^{\ast }{y}_i(x_i\cdot x_j){\lambda }_j\ge 0\end{array}$$由此我们看出，SVM超平面参数只依赖数据集中${\lambda }_i^{\ast }>0$对应的样本点$(x_i,y_i)$

最终SVM的分类决策函数为
$$f(x)=sign(w^{\ast }\cdot x+b^{\ast })$$综上，对线性可分数据集，先求对偶问题的解${\lambda }^{\ast }$；再求解原始问题的解$w^{\ast }$，并使用${\lambda }^{\ast }$的一个正分量${\lambda }_j^{\ast }$求解$b^{\ast }$；最终得到分离超平面和分类决策函数。

2.3 解法二：直接使用KKT条件

满足KKT条件的点为KKT点，在凸问题（包括凸二次规划）中KKT点就是问题的最优解。
通过求解下面的方程组（SVM不含等式约束）来得到KKT点：
$$\{\begin{array}{rl}& \nabla f+\sum _{i=1}^N\lambda \nabla g_i=0\\ & g_i\le 0,i=1,2,...,N\\ & {\lambda }_i\ge 0\\ & {\lambda }_i{h}_i=0\end{array}$$
对SVM的优化问题$$\begin{gathered} \underset{w,b}{\min }f=\frac{1}{2}||w|{|}^2 \\ s.t.g_i=1-y_i(w\cdot x_i+b)\le 0,i=1,2,...,N \end{gathered}$$其KKT条件为：
$$\{\begin{array}{rl}& w-\sum _{i=1}^N{\lambda }_i{y}_i{x}_i=0\\ & \sum _{i=1}^N{\lambda }_i{y}_i=0\\ & {\lambda }_i(1-y_i(w\cdot x_i+b))=0,i=1,2,...,N\\ & 1-y_i(w\cdot x_i+b)\le 0,i=1,2,...,N\\ & {\lambda }_i\ge 0,i=1,2,...,N\end{array}$$

3. SVM编程求解

3.1 问题样例

数据集包含三个样例，正样例点是$x_1=(3,3{)}^T$，$x_2=(4,3{)}^T$，负样例点是$x_3=(1,1{)}^T$。

3.2 KKT方程组

样本空间为三维，将超平面定义为$y=w_1{x}_1+w_2{x}_2+b$。由KKT条件，得到如下方程组：
$$\{\begin{array}{rl}& w_1=3{\lambda }_1+4{\lambda }_2-{\lambda }_3\\ & w_2=3{\lambda }_1+3{\lambda }_2-{\lambda }_3\\ & {\lambda }_1+{\lambda }_2-{\lambda }_3=0\\ & {\lambda }_1(1-(3w_1+3w_2+b))=0\\ & {\lambda }_2(1-(4w_1+3w_2+b))=0\\ & {\lambda }_3(1+(w_1+w_2+b))=0\\ & 1-(3w_1+3w_2+b)\le 0\\ & 1-(4w_1+3w_2+b)\le 0\\ & 1+(w_1+w_2+b)\le 0\\ & {\lambda }_1\ge 0\\ & {\lambda }_2\ge 0\\ & {\lambda }_3\ge 0\end{array}$$

3.3 MATLAB求解

使用MATLAB的solve函数对KKT方程组的前六个等式方程组求解，得到多个解组成的解集，然后筛选出解集中的满足所有剩余不等式约束的解，即问题的最终解。最后并绘制超平面可视化，相关代码及效果如下。

clear
close all
clc
tic

%% 样本点
% (3, 3)--(1)  (4, 3)--(1)  (1, 1)--(-1)
x1 = [3 3]; y1 = +1;
x2 = [4 3]; y2 = +1;
x3 = [1 1]; y3 = -1;

%% 对等式方程组求解
syms lambda1 lambda2 lambda3 w1 w2 b
vars = [lambda1 lambda2 lambda3 w1 w2 b];

eqn1 = lambda1*x1(1)*y1 + lambda2*x2(1)*y2 + lambda3*x3(1)*y3 == w1;  % 对w1的梯度
eqn2 = lambda1*x1(2)*y1 + lambda2*x2(2)*y2 + lambda3*x3(2)*y3 == w2;  % 对w2的梯度
eqn3 = lambda1*y1 + lambda2*y2 + lambda3*y3 == 0;                     % 对b的梯度
eqn4 = lambda1*(1-y1*(x1(1)*w1+x1(2)*w2+b)) == 0;                     % 互补松弛
eqn5 = lambda2*(1-y2*(x2(1)*w1+x2(2)*w2+b)) == 0;                     % 互补松弛
eqn6 = lambda3*(1-y3*(x3(1)*w1+x3(2)*w2+b)) == 0;                     % 互补松弛

eqns = [eqn1, eqn2, eqn3, eqn4, eqn5, eqn6];
S = solve(eqns, vars);

%% 满足剩余不等式约束
n = length(S.b);
flag = false;
for i = 1:n
    lambda1_ = S.lambda1(i);
    lambda2_ = S.lambda2(i);
    lambda3_ = S.lambda3(i);
    w1_ = S.w1(i);
    w2_ = S.w2(i);
    b_ = S.b(i);
    if (lambda1_ >= 0)...
            && (lambda2_ >= 0)...
            && (lambda3_ >= 0)...
            && ((3*w1_ + 3*w2_ + b_) >= 1)...
            && ((4*w1_ + 3*w2_ + b_) >= 1)...
            && (-(w1_ + w2_ + b_) >= 1)
        fprintf('lambda1 = %s  \nlambda2 = %s  \nlambda3 = %s  \nw1 = %s  \nw2 = %s  \nb = %s \n',...
            lambda1_, lambda2_, lambda3_, w1_, w2_, b_)
        flag = true;
        break
    end
end
if ~flag
    fprintf('无解\n')
end

%% 绘图
x_all = [x1(1), x2(1), x3(1)];
y_all = [x1(2), x2(2), x3(2)];
z_all = [y1, y2, y3];
X = linspace(min(x_all)-2, max(x_all)+2, 60);
Y = linspace(min(y_all)-2, max(y_all)+2, 60);
[X, Y] = meshgrid(X, Y);
Z = double(w1_) .* X + double(w2_) .* Y + double(b_);
figure(1)
colormap('jet')
mesh(X, Y, Z)
% view(23, -18)
view(57, 19)
hold on
plot3(x_all, y_all, z_all, 'bo', 'MarkerFaceColor', 'k', 'MarkerSize', 8) 
hold off
axis([-inf, inf, -inf, inf, -2, 2])
xlabel('x1')
ylabel('x2')
zlabel('y')

toc

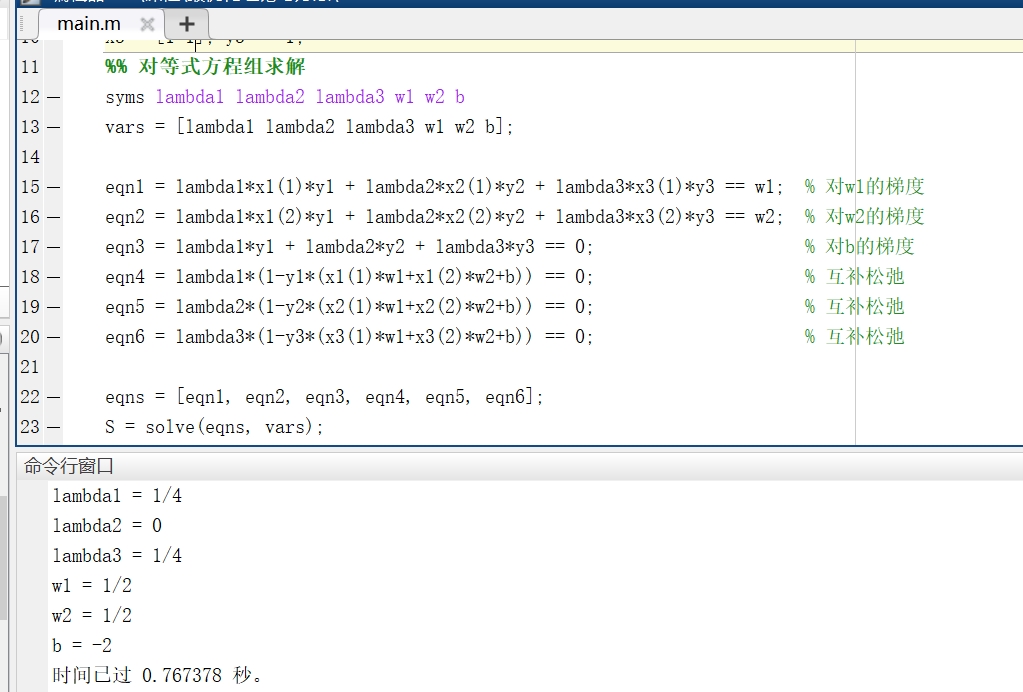
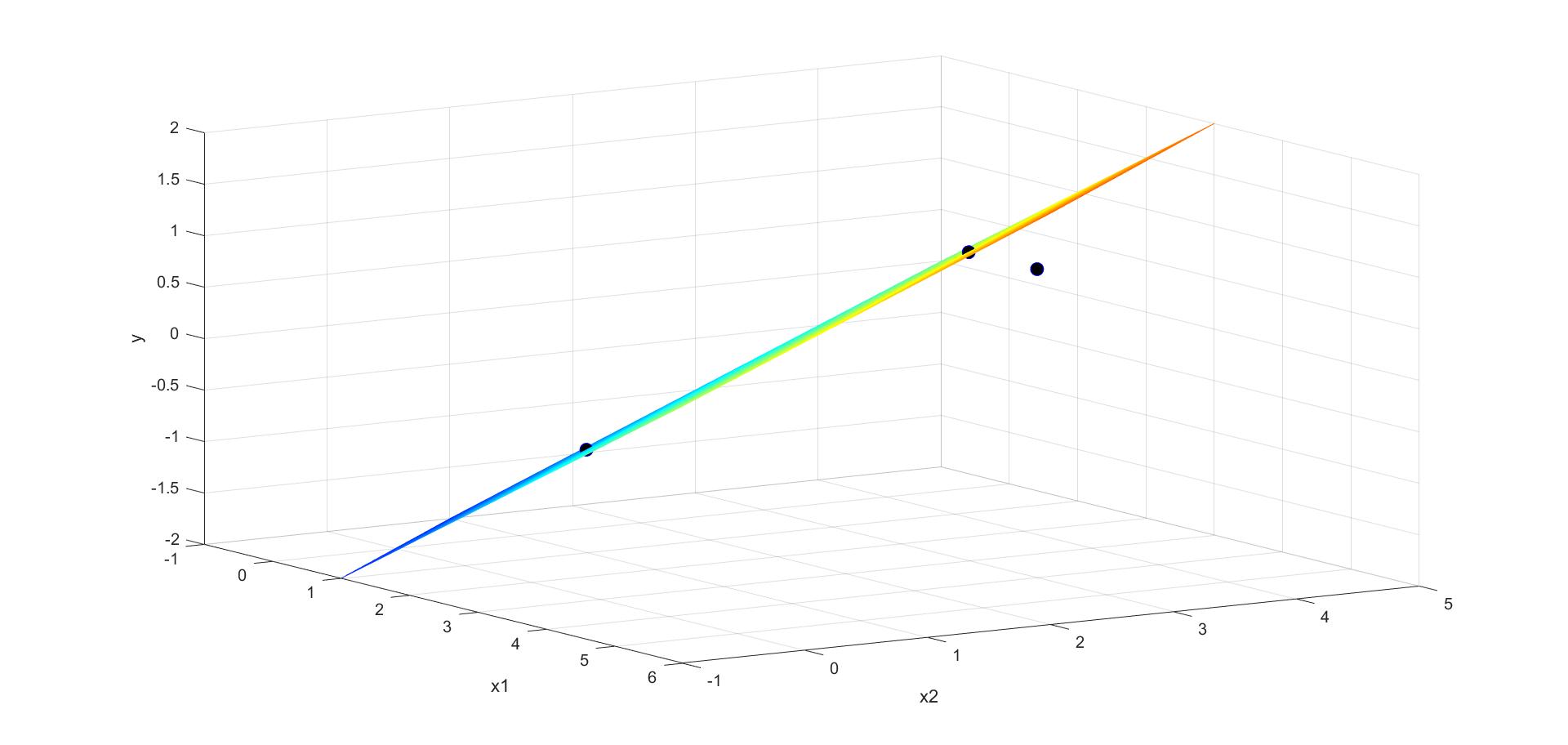
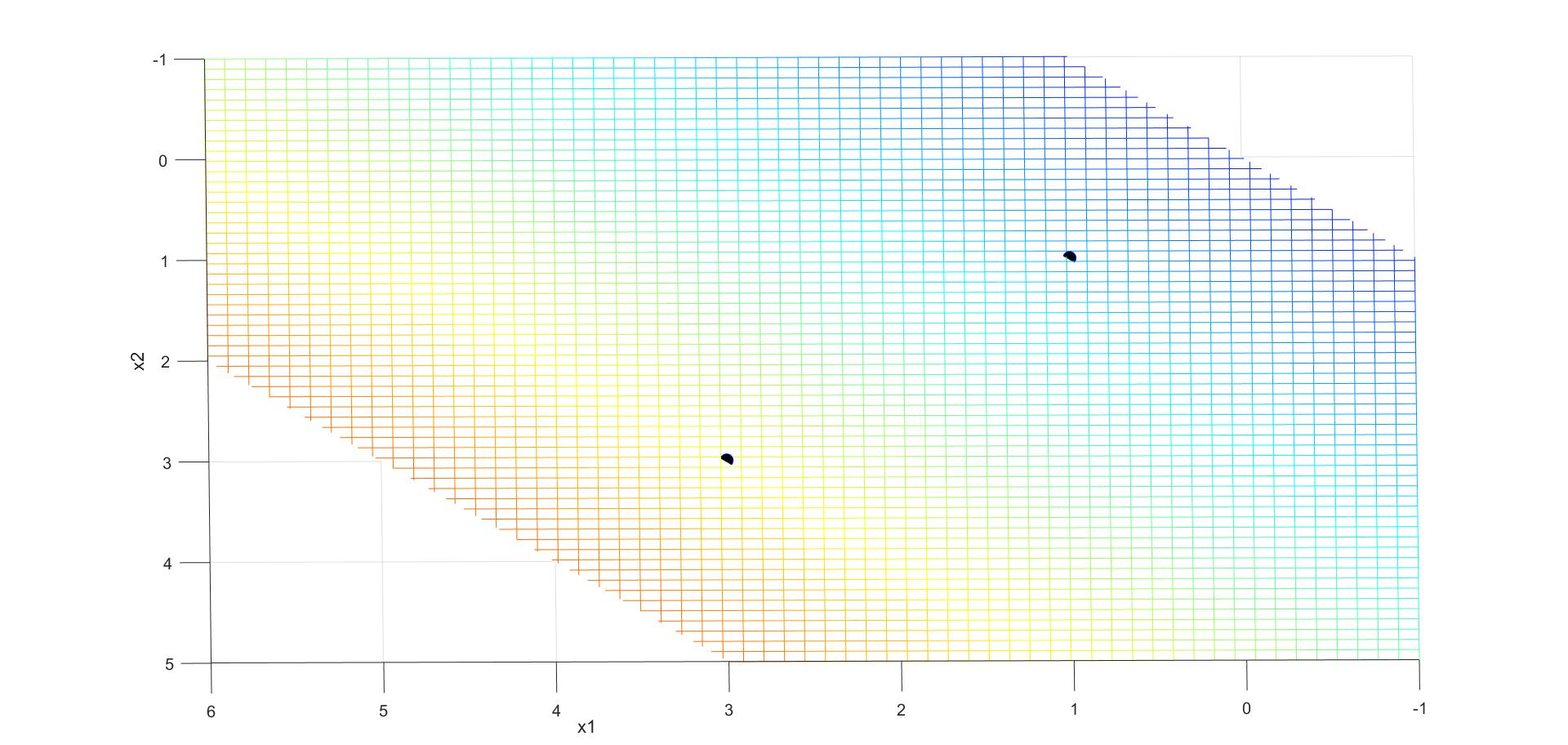
得到的分离超平面为$y=\frac{1}{2}{x}_1+\frac{1}{2}{x}_2-2$，由可视化结果可以看出，$(3,3{)}^T$和$(1,1{)}^T$为支持向量。

4. 总结

1. 以SVM为研究对象，并由最大化几何间隔，最终建立起SVM的约束最优化问题。
2. 以对偶问题、KKT条件、凸规划问题的性质等为切入点，一步步推导出SVM的最优解。
3. 设计了一个实例，建立KKT方程组，并使用MATLAB编程求解，得到分离超平面，通过可视化超平面得到支持向量。

在整个过程中，通过学习、推导与应用，加深了对线性可分支持向量机的理解，并深入理解了KKT条件的组成与背后逻辑，也了解了KKT条件的应用价值。