BP_NSGA2)BP神经网络做代理预测模型，多目标遗传NSGA2寻优求最佳因变量对应的最佳自变量组合和帕累托前沿解三个因变量：求解最大y1(最大效率) 求解最小y2(最小经济成本）最小y3最小y4

BP_NSGA2)BP神经网络做代理预测模型，多目标遗传NSGA2寻优求最佳因变量对应的最佳自变量组合和帕累托前沿解

三个因变量：求解最大y1(最大效率)

            求解最小y2(最小经济成本）

            求解最小y3(最小时间成本)

                                求最小y4

(懒人救星版)BP _NSGA2

懒人救星版：

     1.任意多输入多输出都可以用(采用四套数据集)

4输入2输出.xlsx  4输入3输出.xlsx   5输入3输出.xlsx

4输入4输出.xlsx

     2.加入数据拟合散点图

数据特点：（多元化的数据）

包含0-1数据、大于1的数据和极大的数据（10的8次方）

每个代码压缩文件包改动代码处不超过6处

如下图代码中：（改动点总计4处代码即可运行）

1. BP神经网络的算法原理及主要应用

示意图：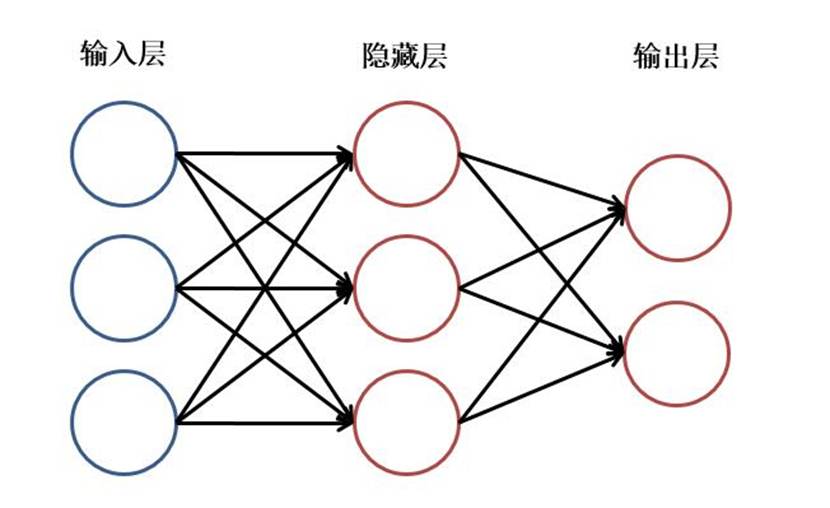

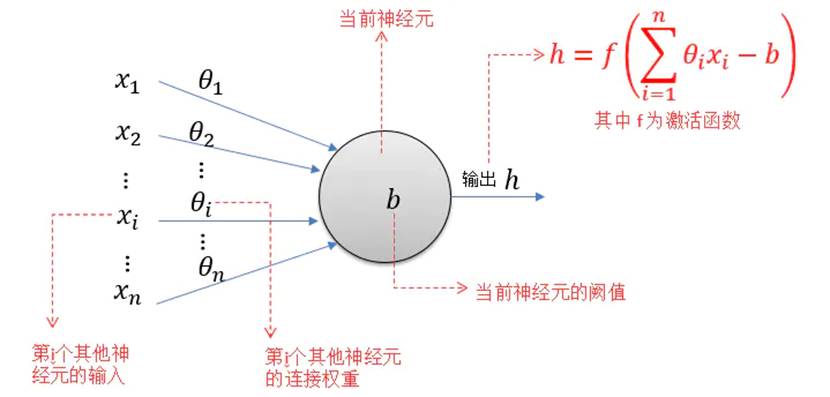
（1）信号向前传递的过程

假设隐含层的第i个神经元节点上输入neti的值，其表达式（2.1）：

                      (2.1)

隐含层的第i个神经元节点的输出，其表达式（2.2）：

                                  (2.2)

选用logsig函数作为神经网络隐含层的传递函数，其表达式 (2.3)：

                                               (2.3)

选用pureline型函数作为神经网络输出层的传递函数，其表达式(2.4)：

                                                   (2.4)

输出层第k个神经元节点的输入的值，其表达式（2.5）：

                       (2.5)

输出层第k个神经元节点的输出其表达式（2.6）：

                     (2.6)

（2）误差反向传播过程

神经网络在训练时，误差的反向传播过程，其实就是用训练模型的输出层上所有神经元的值减去实际值获得误差值，在通过反向传播来不断地调整权值和阈值。通过求得的误差，对各层神经元权值及阈值的偏导数方向和大小进行修正，一直到误差达到我们预设的条件为止，训练结束[44]。

根据总误差函数，对于数据m的误差函数，其表达式（2.7）：

                                            (2.7)

样本中有p个训练数据组，总误差函数，其表达式（2.8）：

                                       (2.8)

根据修改的连接参数值，整理获得系统输出层与隐含层之间的权值 连接参数，其表达式（2.9）：

               (2.9)

输出层神经元节点上的阈值的变化量，其表达式（2.10）：

                  (2.10)

隐含层与输入层之间的权值的变化量，其表达式（2.11）：

                 (2.11)

隐含层各神经元节点的阈值的变化量，其表达式（2.12）：

               (2.12)

其中：

                                    (2.13)

                                              (2.14)

                                                (2.15)

                                        (2.16)

                                            (2.17)

                         (2.18)

                                    (2.19)

                                 (2.20)

通过最后整理得到了输入层、输出层所对应修正后的权值和阈值：

                      (2.21)

                (2.22)

                          (2.23)

               (2.24)

式中：为输入层第j个神经元节点到隐含层第i个神经元节点之间的权值；x 、y 分别为节点的输入量和节点的输出量；为隐含层第i个神经元节点到输出层第k个神经元节点之间的权值；为输入层第j个神经元节点的输入；i为隐含层第i个神经元节点的阈值；为隐含层的传递函数；为输出层第k个神经元节点的阈值；为输出层传递函数；为输出层第k个神经元节点的输出。

PSO粒子群算法（寻优算法，寻找最优值）

·算法起源：

粒子群优化算法(PSO)是一种进化计算技术(evolutionary computation)，1995 年由Eberhart 博士和kennedy 博士提出，源于对鸟群捕食的行为研究 。该算法最初是受到飞鸟集群活动的规律性启发，进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。

·官方定义

粒子群算法，也称粒子群优化算法或鸟群觅食算法（Particle Swarm Optimization），缩写为 PSO， 是近年来由J. Kennedy和R. C. Eberhart等开发的一种新的进化算法(Evolutionary Algorithm - EA)。PSO 算法属于进化算法的一种，它从随机解出发，通过迭代寻找最优解，通过适应度来评价解的品质，它比遗传算法更为简单，它没有遗传算法的“交叉” (Crossover) 和“变异” (Mutation) 操作，它通过追随当前搜索到的最优值来寻找全局最优。这种算法以其实现容易、精度高、收敛快等优点引起了学术界的重视，并且在解决实际问题中展示了其优越性。粒子群算法是一种并行算法

·通俗定义（生物学理）

如同前面的描述，PSO模拟的是鸟群的捕食行为。设想这样一个场景：一群鸟在随机搜索食物，在这个区域里只有一块食物，所有的鸟都不知道食物在那里，但是它们知道当前位置的好坏（距离食物越近的位置就越好）。那么找到食物的最优策略是什么呢？最简单有效的就是搜寻目前离食物最近的鸟的周围区域。

鸟群在整个搜寻的过程中，通过相互传递各自的信息，让其他的鸟知道自己的位置，通过这样的协作，来判断自己找到的是不是最优解，同时也将最优解的信息传递给整个鸟群，最终，整个鸟群都能聚集在食物源周围，即找到了最优解。

在PSO中，每只鸟的位置都是优化问题解空间中的一个解。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitness value)，每个粒子还有一个速度决定它们飞翔的方向和速率。然后，粒子们就追随当前的最优粒子在解空间中搜索。

在初始化阶段，PSO生成一群随机粒子(即随机解)，然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个"极值"来更新自己。第一个极值就是粒子本身所找到的历史最优解，这个解叫做个体极值pBest。另一个极值是整个种群找到的历史最优解，这个极值是全局极值gBest。

·速度和位置的更新

    位置（）

速度（变化方向，速度）

PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次的迭代中，粒子通过跟踪两个“极值”(pbest，gbest)来更新自己。在找到这两个最优值后，粒子通过下面的公式来更新自己的速度和位置。

公式(1)的第①部分称为【记忆项】，表示上次速度大小和方向的影响；

公式(1)的第②部分称为【自身认知项】，是从当前点指向粒子自身最好点的一个矢量，表示粒子的动作来源于自己经验的部分；

公式(1)的第③部分称为【群体认知项】，是一个从当前点指向种群最好点的矢量，反映了粒子间的协同合作和知识共享。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。

以上面两个公式为基础，再来看一个公式：

·标准PSO算法的流程

1）初始化一群微粒(群体规模为N)，包括随机位置和速度；

2）评价每个微粒的适应度；

3）对每个微粒，将其适应值与其经过的最好位置pbest作比较，如果较好，则将其作为当前的最好位置pbest；

4）对每个微粒，将其适应值与其经过的最好位置gbest作比较，如果较好，则将其作为当前的最好位置gbest；

5）根据公式(2)、(3)调整微粒速度和位置；

6）未达到结束条件则转第2）步。

迭代终止条件根据具体问题一般选为最大迭代次数Gk或(和)微粒群迄今为止搜索到的最优位置满足预定最小适应阈值。

·PSO算法流程图

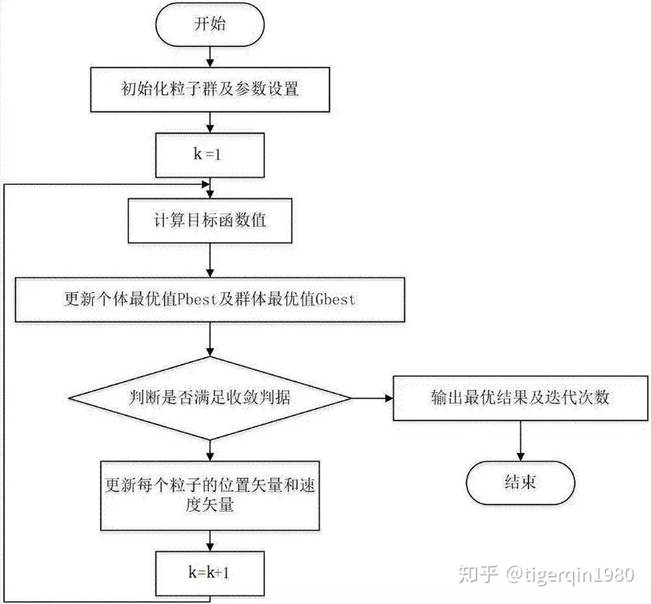
·学习因子c1、c2分析

公式(2)和(3)中pbest和gbest分别表示微粒群的局部和全局最优位置。

当c_1＝0时，则粒子没有了认知能力，变为只有社会的模型(social-only)：

称为全局PSO算法。粒子有扩展搜索空间的能力，具有较快的收敛速度，但由于缺少局部搜索，对于复杂问题比标准PSO 更易陷入局部最优。

当c_2＝0时，则粒子之间没有社会信息，模型变为只有认知(cognition-only)模型：

称为局部PSO算法。由于个体之间没有信息的交流，整个群体相当于多个粒子进行盲目的随机搜索，收敛速度慢，因而得到最优解的可能性小。

首先，Topsis，也就是逼近理想解排序法，是一种多准则决策分析方法。它的基本思想是通过计算各方案与理想解（正理想解）和负理想解之间的距离来进行排序。理想解是各指标的最优值，负理想解是各指标的最劣值。然后根据相对接近度来排序，相对接近度越高，方案越优。

然后是熵权法，这是一种客观赋权方法，用于确定各指标的权重。熵原本是热力学中的概念，后来在信息论中用于衡量信息的不确定性。熵权法通过计算各指标的熵值来判断该指标的离散程度，离散程度越大，熵值越小，信息量越大，权重也就越高。反之，离散程度越小，熵值越大，权重越低。

Topsis 熵权法是指在 Topsis 中使用熵权法来确定各指标的权重，而不是主观赋权。这样可以让权重的确定更客观，减少主观因素的影响。

Topsis 熵权法是一种结合了逼近理想解排序法（Topsis）和熵权法的多准则决策分析方法，主要用于解决多指标评价问题。其核心思想是通过熵权法客观确定指标权重，再利用 Topsis 对方案进行排序。

原理如下：

包括数据标准化、熵权计算、加权矩阵构建、理想解确定、距离计算和排序

1. 数据标准化

2. 熵权法计算指标权重

熵权法通过指标的信息量客观确定权重，步骤如下：

3. 构建加权标准化矩阵

4. 确定正理想解和负理想解

NSGA-2 和 NSGA-3 主要有以下区别：

• 提出时间与背景1
  • NSGA-2：1992 年由 Deb 等人提出，是经典多目标优化算法，旨在改进 NSGA 算法，解决其在非支配排序时间复杂度高、不支持精英策略和需指定共享参数等问题。
  • NSGA-3：2013 年由 Deb 提出，是基于 NSGA-2 针对高维多目标优化问题改进的算法。因为 NSGA-2 处理三个及以下目标问题表现良好，但处理高维问题时性能会下降。
• 非支配排序策略3
  • NSGA-2：将个体按支配关系划分到不同层级，然后按层级从前往后排序。例如，在一个双目标优化问题中，通过比较每个个体在两个目标上的表现，确定其是否被其他个体支配，从而划分层级。
  • NSGA-3：通过将个体按照参考点所在的超平面划分到不同集合中，然后按照集合的优先级从前往后排序。先寻找理想点，构建超平面并进行目标归一化，再根据个体与参考点的关系进行划分。
• 选择机制
  • NSGA-2：使用拥挤度距离作为衡量标准之一，在同一非支配等级里更倾向于边界上的样本。通过计算每个个体在目标空间中周围个体的密度，选择密度较小区域的个体，以保持种群的多样性。
  • NSGA-33：借助预先设置的一系列理想化的目标组合，即 “参考点”，引导搜索路径趋向理想的帕累托前沿形状。计算个体与参考点之间的距离来选择出最优解集，使算法更好地探索前沿解集的不同部分。
• 适用场景3
  • NSGA-2：适用于最多三个目标的多目标优化问题。在低维问题中，能够快速找到帕累托前沿，并保持较好的种群多样性。
  • NSGA-3：更适合处理高维多目标优化问题，即四个及以上目标的优化问题。在面对高维复杂环境时，能更精准地逼近真实最优解集，在解集的分布性和多样性方面表现更优。
• 种群多样性维持方式
  • NSGA - 212：在 NSGA-2 中用拥挤比较的方法替换了共享函数方法，根据每一目标函数计算个体两侧的两个点的平均距离，以最近邻居作为顶点的长方体周长的估计值作为拥挤系数，选择拥挤系数大的个体来维持多样性。
  • NSGA - 31：采用种群的自适应标准化和关联操作。通过寻找理想点、计算极值点、构建超平面找到截距并进行目标归一化，让群体中的个体分别关联到相应的参考点，从而维持种群多样性。

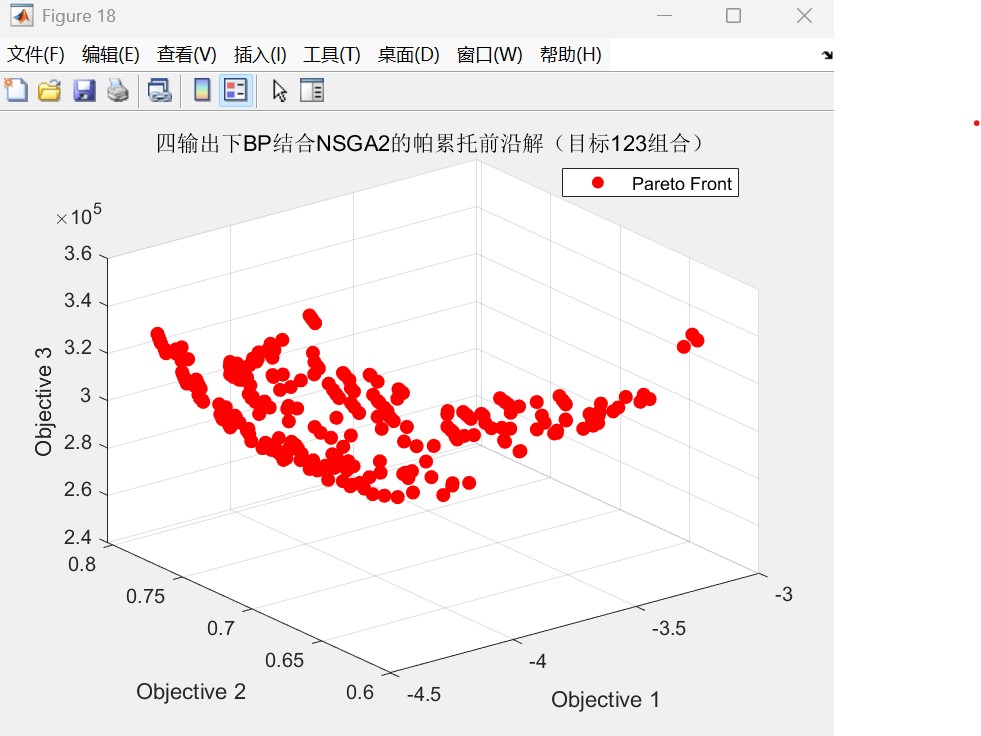
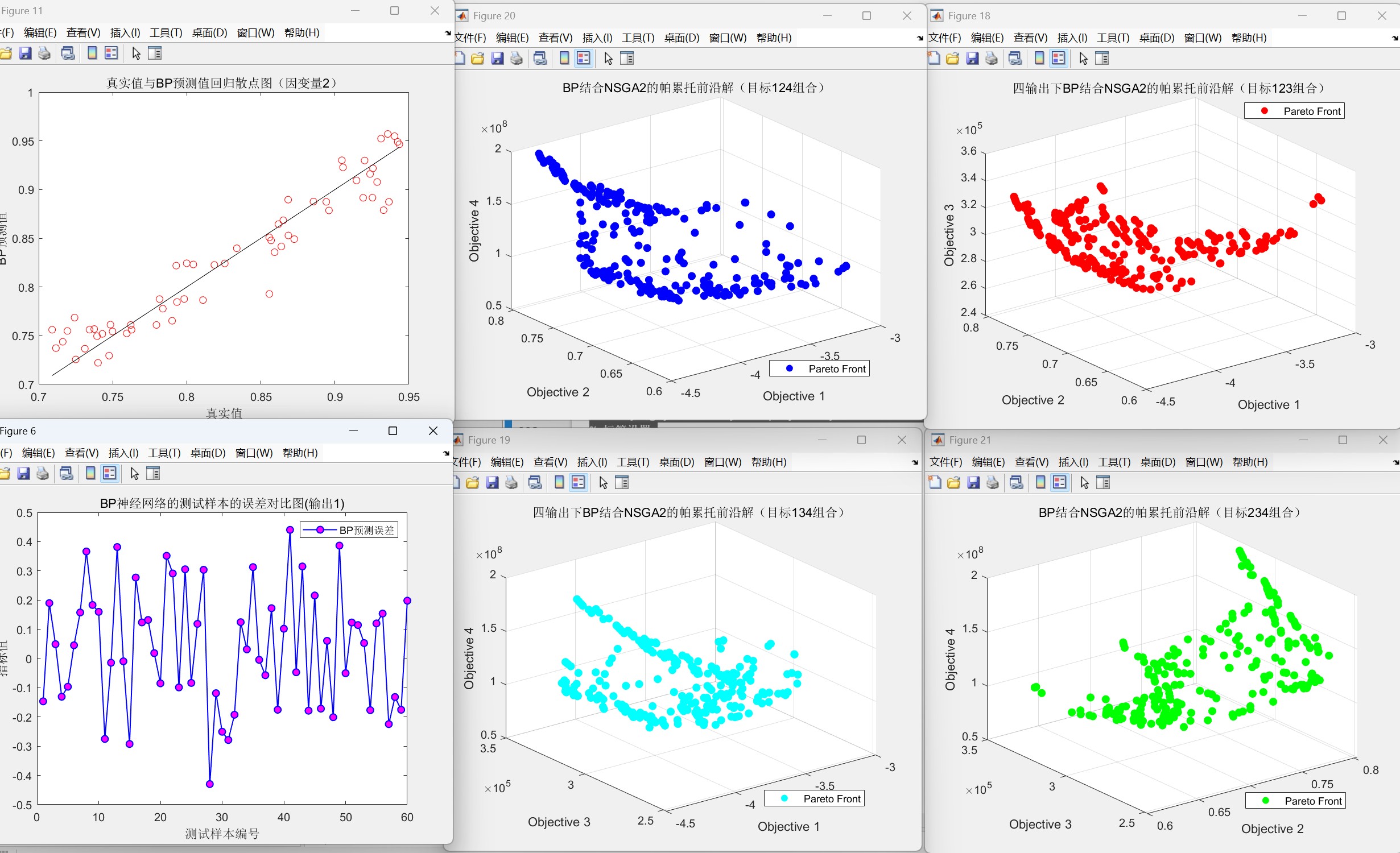
代码运行效果图（以三维三目标为例如下：）：

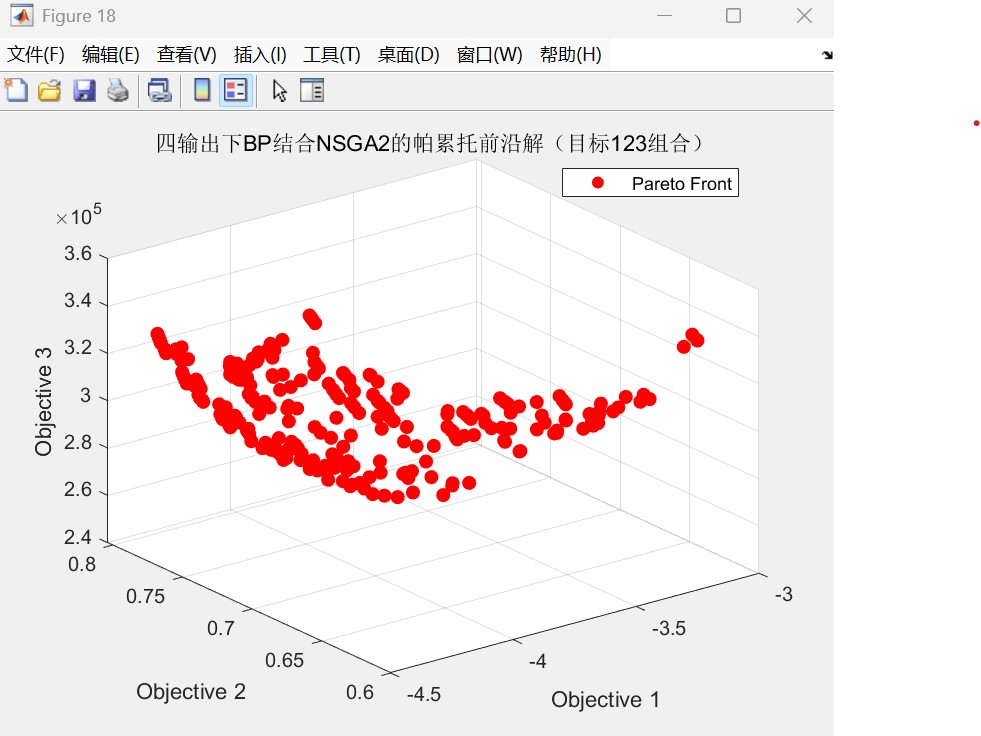
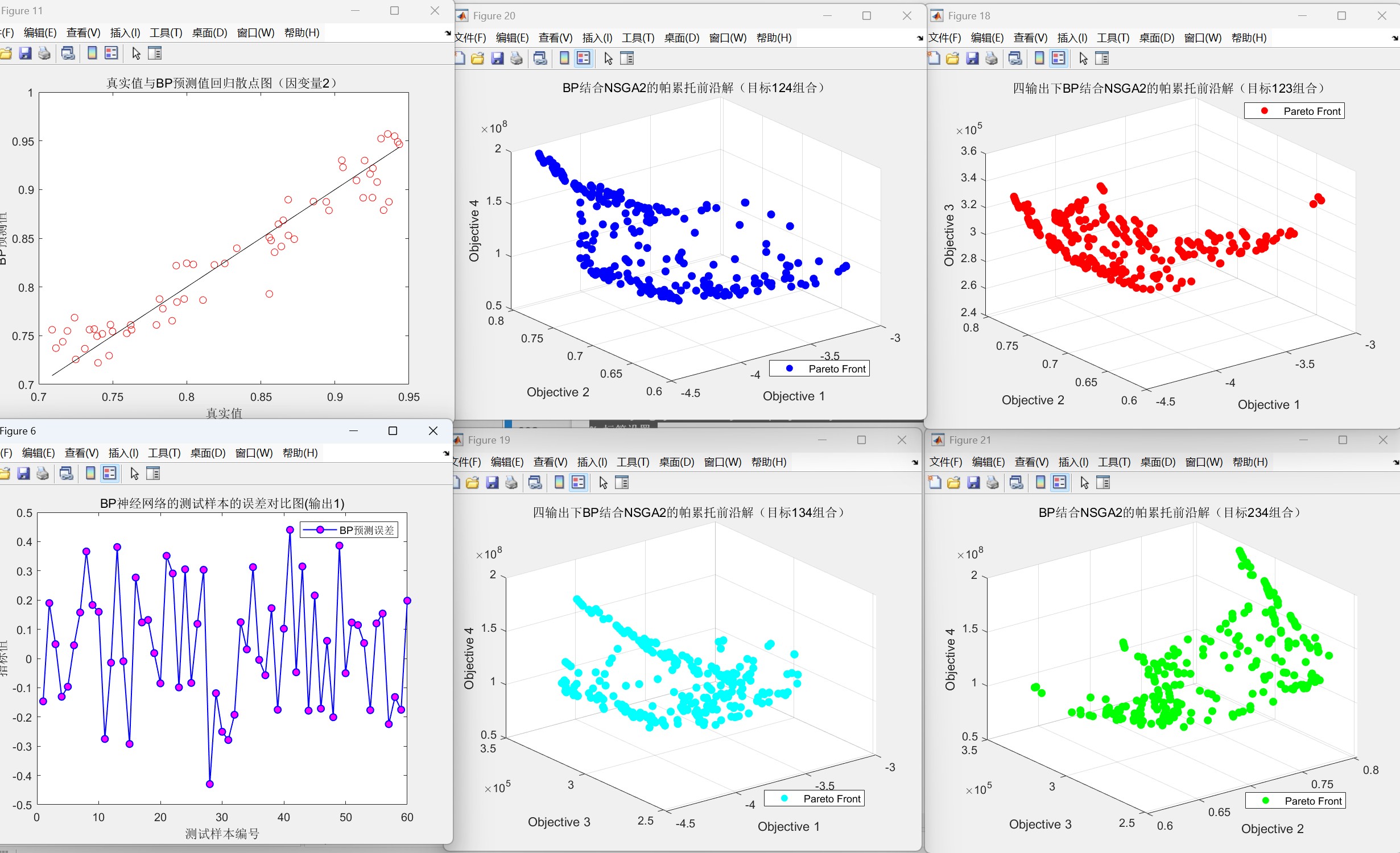
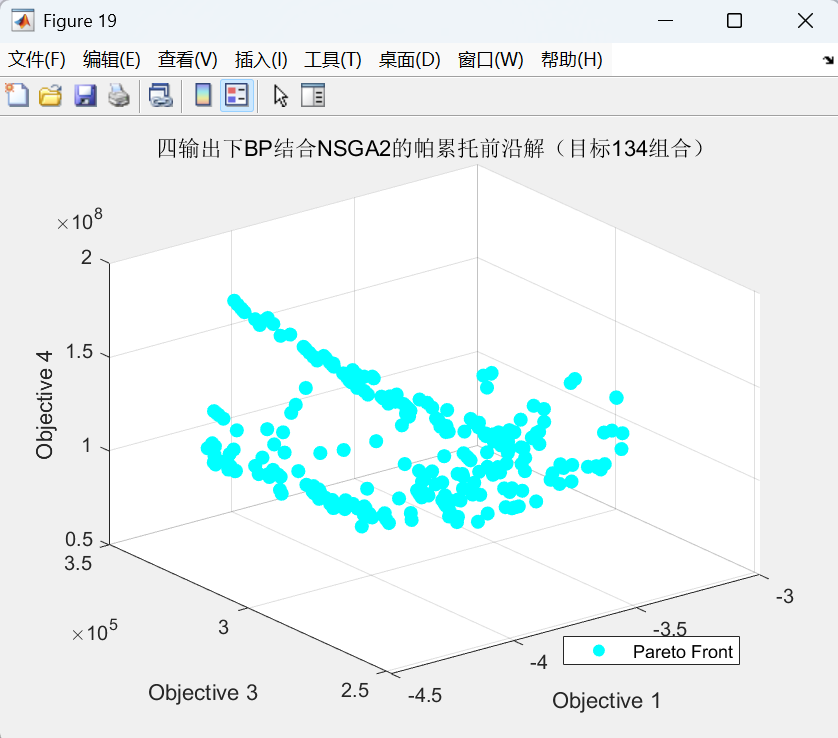
帕累托前沿图：

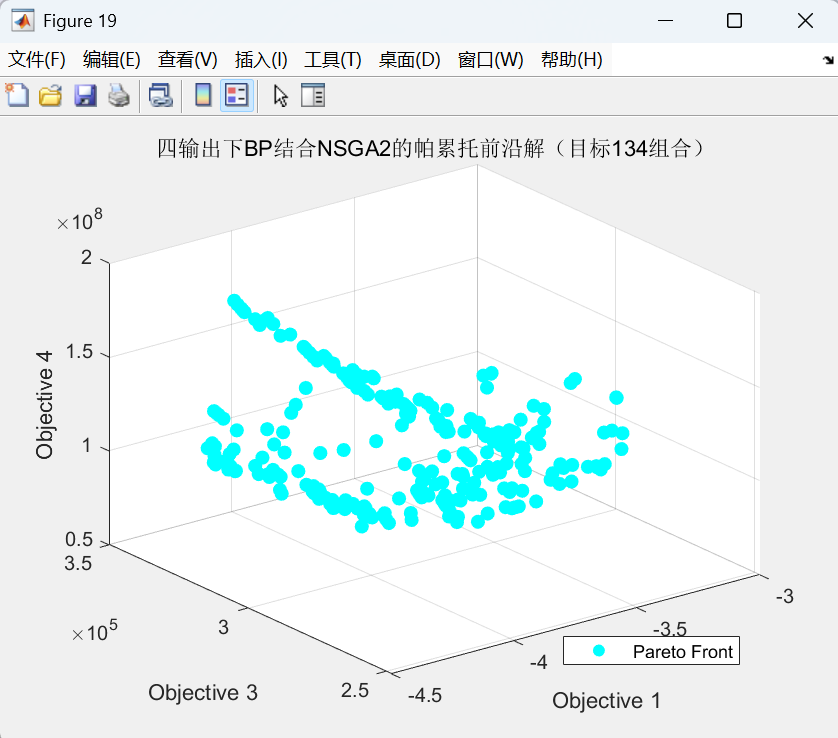
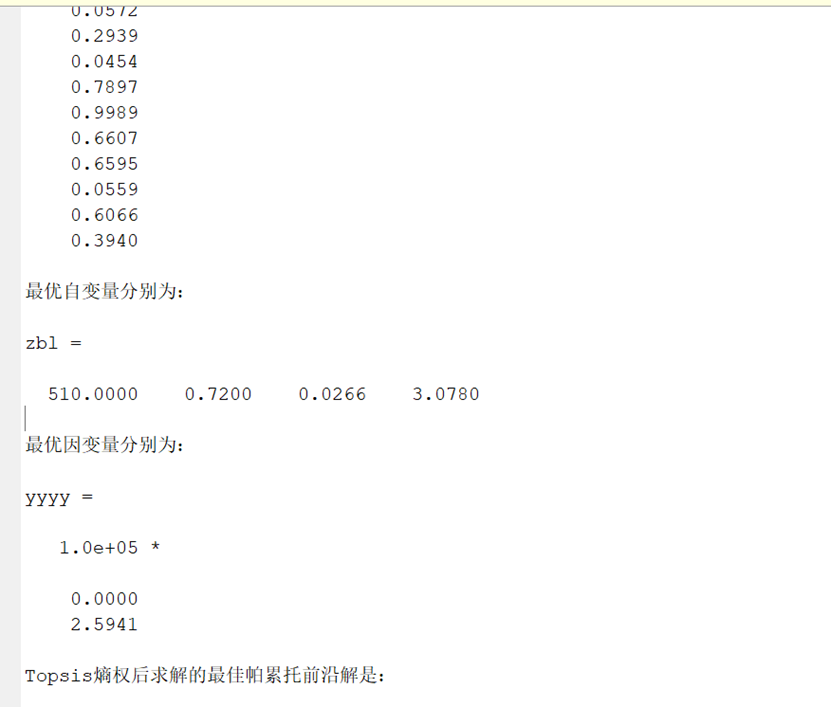
Topsis求解的各解相对接近度如下：

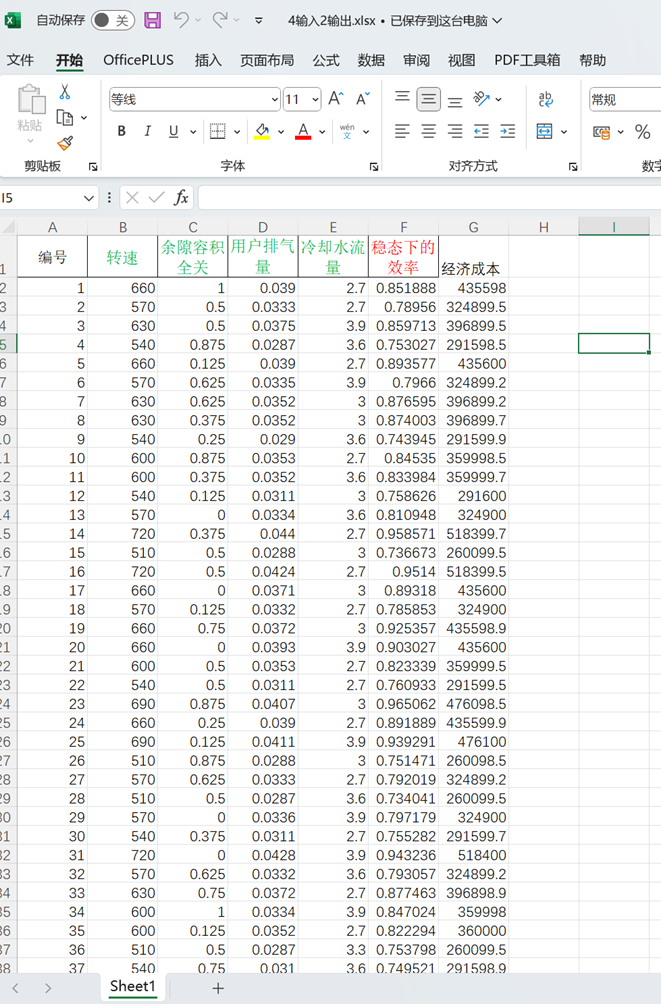
采用的数据集如下：

4输入2输出.xlsx如下：

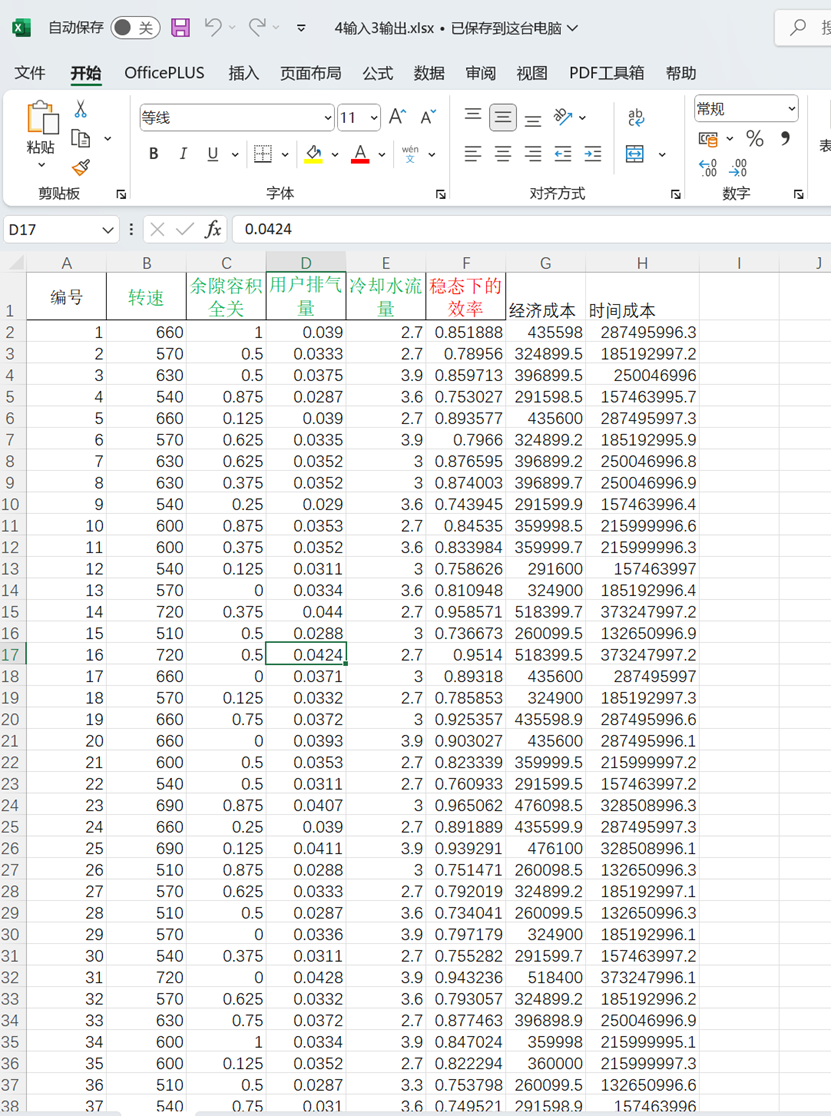
4输入3输出.xlsx如下：

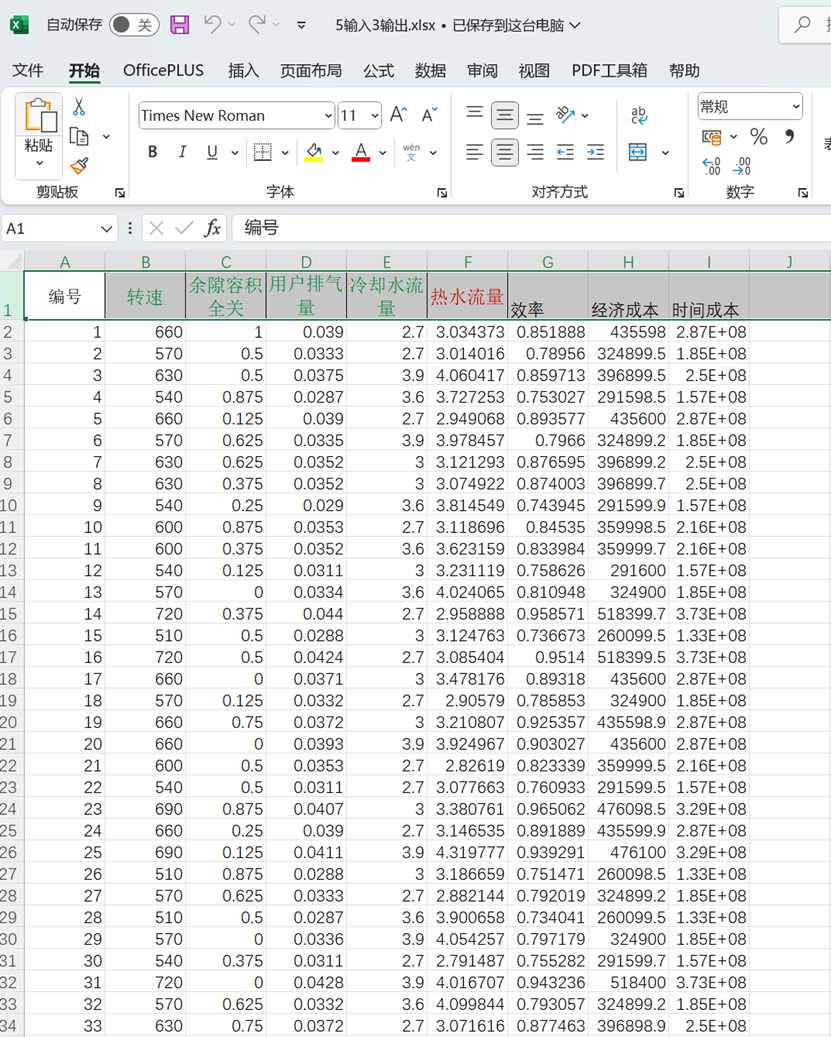
5输入3输出如下：

​​编辑​