【模型的量化 神经网络量化】对称量化与非对称量化 无符号数量化 有符号数量化

减少模型大小：通过将模型的权重和激活值从浮点数（如32位的FP32）转换为低精度的格式（如8位的INT8），可以显著减少模型的存储大小。这种压缩可以使得模型更易于在各种设备上部署，包括资源受限的环境。

降低内存带宽和存储需求：量化后的模型由于尺寸减小，对内存的依赖也随之降低，这减少了内存的访问带宽需求，提高了缓存命中率，特别是在处理内存密集型操作时效果显著。

提高计算速度：使用低精度的数据类型可以提高计算速度，因为现代处理器对低精度数据的计算支持更好，能够实现更快的处理速度。这对于实时应用和需要快速响应的场景尤其重要。

降低功耗：在移动设备上，使用8位数据而不是32位浮点数可以显著降低功耗，这对于延长电池寿命和提高设备的能效比非常关键。

提高系统吞吐量和降低延时：量化可以使芯片的计算峰值增加，因为一条指令可以同时处理更多的数据。这提高了系统的吞吐量并降低了处理延时，尤其是在使用SIMD指令集时效果显著。

适应硬件发展：随着专用深度学习加速器和支持INT8运算的硬件（如DSP、GPU）的发展，量化模型能够更好地利用这些硬件的能力，实现更高效的运算。

推动深度学习模型的商业化和普及：量化技术使得深度学习模型能够更容易地集成到商业产品中，尤其是在边缘计算和移动设备上，这推动了深度学习技术的商业化和普及。

解决部署难题：量化模型更容易在不同的硬件平台上部署，因为它们对计算资源的要求较低，这解决了将深度学习模型部署到资源受限设备上的难题。

从图中我们可以看到32bit浮点数计算，能量对比上远远高于8bit能量的计算消耗的。因此目前大模型通常8bit量化更有利于边缘设备部署。

量化方法

1.非对称量化

1.1 无符号量化（uint8)

将原始数据xf 最大值max(xf)，最小值min(xf)映射到 0-255的区间上。

公式：


随机写入一组float32的tensor:

x=torch.tensor([[ 0.9872, -1.6833], [-0.9345, 0.6531]])

这里输出的s我们自己手动计算得到s,z：

1.2 有符号量化（int8)

将原始数据xf 最大值max(xf)，最小值min(xf)映射到 -127，127的区间上。工程上常用有符号是-127-127

公式：


写入一组相同float32的tensor:

x=torch.tensor([[ 0.9872, -1.6833], [-0.9345, 0.6531]])

这里输出的s我们自己手动计算得到s,z，区别在于此时的qmax 从255变成127：

1.3 代码

import torch


#清空cuda内存
torch.cuda.empty_cache()

print("---------非对称量化----------")

x=torch.tensor([[ 0.9872, -1.6833],
         [-0.9345,  0.6531]])
print(x)
# 公式1(量化)：xq = round(x / scale + zero_point)
# 使用给定的scale和 zero_point 来把一个float tensor转化为 quantized tensor
#随机设定的scale和 zero_point
# 有符号数
xq = torch.quantize_per_tensor(x, scale=0.0104725, zero_point=33, dtype=torch.qint8)

#无符号数
xq1 =torch.quantize_per_tensor(x,scale=0.0104725,zero_point=161,dtype=torch.quint8)
print("xq",xq) #输出一个经过反量化的张量
print("xq1",xq1) #输出一个经过反量化的张量
print("xqint8",xq.int_repr())  # 给定一个量化的张量，返回一个以 uint8_t 作为数据类型的张量
print("xquint8",xq1.int_repr())

# 公式2(反量化)：xdq = (xq - zero_point) * scale
# 使用给定的scale和 zero_point 来把一个 quantized tensor 转化为 float tensor
xdq = xq.dequantize()
print(xdq)

1.4总结

程序中torch量化类型quint，qint，分别存在反量化之后的数值，和量化的整型数值。这个是qint对象的特点。通过int_repr()看到中间量化的结果。
此外，量化存在精度损失。有符号和无符号的非对称量化改变的是数值量化的范围，反量化的结果存在误差损失。

2 对称量化

对称量化和非对称量化的区别在于，是否把输入的float区间看成一个对称的。这常常用于权重量化，或者常常用于一些分布对称的数值区间进行量化。

2.1 无符号量化（uint8)

区别主要在于对称量化为对称区间，零点在127.


比例因子s 的计算可以是上述的也可以直接，s=max(xf)/127.误差一般都是相同的。

2.2 有符号量化（uint8)

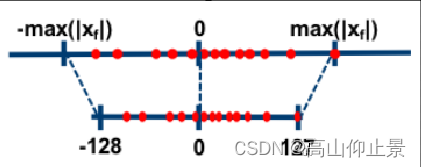
区别主要在于对称量化为对称区间，零点在0，一般对称量化的类型都是有符号类型。常用于权重的量化。

2.3总结

非对称量化VS对称量化

非对称量化相比于对称量化而言，无需遵循0不变的映射规则，显然具有更好的动态映射范围，并且当面临一些特殊情况，如对于经过relu的激活值（全为非负值），使用对称量化时，需要仔细考虑使用符号量化，还是无符号量化。

但另一方面非对称量化相对于对称量化需要付出更大的计算代价

可以看到，后两项都是常量，可以提前离线计算好，但额外多出的第二项相比于对称量化而言，非对称量化有着较大的额外计算开销。

综合以上分析，硬件支持的前提下，量化时对激活值X使用非对称量化，对权重值W使用对称量化，或许是一种更适宜的量化方案

2.4 程序代码

print("---------对称量化----------")


x=torch.tensor([[ 0.9872, -1.6833],
         [-0.9345,  0.6531]])
print(x)
# 有符号数

s= 1.6833/127
z0=0

xq = torch.quantize_per_tensor(x, scale=s, zero_point=0, dtype=torch.qint8)
xq1 = torch.quantize_per_tensor(x, scale=s, zero_point=127, dtype=torch.quint8)
print("xq",xq) #输出一个经过反量化的张量

print("xqint8",xq.int_repr())  # 给定一个量化的张量，返回一个以 uint8_t 作为数据类型的张量

print("xq1",xq1) #输出一个经过反量化的张量

print("xq1uint8",xq1.int_repr())  # 给定一个量化的张量，返回一个以 uint8_t 作为数据类型的张量
# 公式2(反量化)：xdq = (xq - zero_point) * scale
# 使用给定的scale和 zero_point 来把一个 quantized tensor 转化为 float tensor
xdq = xq.dequantize()
print(xdq)

以上为对有无符号的量化类型讨论，以具体的张量类型进行程序举例。