sigmoid & tanh激活函数

sigmoid & tanh激活函数介绍：
1.sigmoid 激活函数

tanh 函数是sigmoid函数的一种变体，以0点为中心。取值范围为 [-1,1] ，而不是sigmoid函数的 [0,1] 。

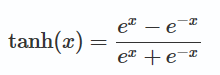
2.tanh 是对 sigmoid 的平移和收缩: tanh(x)=2⋅σ(2x)−1
sigmoid & tanh 函数图像如下:

3.sigmoid作激活函数的优缺点
优势是能够控制数值的幅度,在深层网络中可以保持数据幅度不会出现大的变化;而ReLU不会对数据的幅度做约束.
但存在三个问题:
1.饱和的神经元会"杀死"梯度,指离中心点较远的x处的导数接近于0,停止反向传播的学习过程.
2.sigmoid的输出不是以0为中心,而是0.5,这样在求权重w的梯度时,梯度总是正或负的.
3.指数计算耗时

4.为什么tanh相比sigmoid收敛更快:
1.梯度消失问题程度
tanh′(x)=1−tanh(x)2∈(0,1)
sigmoid: s′(x)=s(x)×(1−s(x))∈(0,1/4)
可以看出tanh(x)的梯度消失问题比sigmoid要轻.梯度如果过早消失,收敛速度较慢.
2.以零为中心的影响
如果当前参数(w0,w1)的最佳优化方向是(+d0, -d1),则根据反向传播计算公式,我们希望 x0 和 x1 符号相反。但是如果上一级神经元采用 Sigmoid 函数作为激活函数，sigmoid不以0为中心，输出值恒为正，那么我们无法进行最快的参数更新，而是走 Z 字形逼近最优解