总结DIP Test ,PDIP Test

最新推荐文章于 2024-04-15 22:15:51 发布

keep_humble

最新推荐文章于 2024-04-15 22:15:51 发布

阅读量1.2k

点赞数 2

分类专栏：论文文章标签：代价函数全局去相局部去相

本文链接：https://blog.csdn.net/qq_43270444/article/details/118520576

版权

论文专栏收录该内容

12 篇文章

订阅专栏

本文详细介绍了量子计算中全局去相和局部去相的概念，并探讨了这两种操作在代价函数设计中的应用。代价函数C1和C2分别对应不同的去相策略，其中C1在大尺寸系统中可能遭遇梯度消失问题，而C2则呈现多项式级别的消失。文章通过电路图和计算过程说明了DIPTest和PDIPTest的实现，并分析了不同代价函数在训练参数时的效果，指出在量子比特数量较大时，C1直接训练可能无法收敛，而C2和结合C1、C2的代价函数可以取得更好的收敛效果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

这篇文章是针对2019年《variational quantum state diagonalization》这篇文章内的全局去相(globally dephase)、以及局部去相（locally dephase）这两种运算（在量子中操作，多指的是酉操作）所进行的总结，因为本文代价函数的设计牵扯到这两个电路，在这个代价函数理解上花费了很长的一段时间，走了不少弯路，特此总结一下。

1.代价函数的设计

2.代价函数C1

假设存在运算Z能够将矩阵非主对角线上的元素置为0，效果图如下：

根据上述代价函数的定义，我们得到：

2.1 DIP Test

电路图如下，此电路实现的是计算代价函数C1的后半部分，即主对角线元素乘积之和。

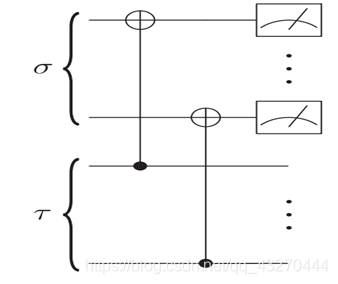
计算过程如下：

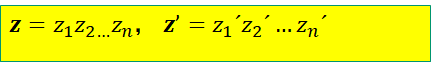
该电路深度为1，执行一次DIP test电路测量次数为n，对于n-qubit的量子态只需要利用n个CNOT门。

3.代价函数C2

代价函数C2是针对某一个qubit张量成的空间进行DIP Test操作，对于其余（n-1)qubit张量成的空间执行的是I操作，我们借助矩阵理解一下什么是局部去相。

我们可以发现，如果对于第一个和第二个qubit都执行去相运算，产生的效果就是全局去相运算：

3.1 PDIP Test

为了计算方便，原文提出不再是对单个qubit进行局部去相，而是I个qubit一起进行局部去相原酸，通过验证发现，结果并没有发生变化，验证如下：

电路图如图所示：

第（3）步骤，是结果得到全零，观测子系统（黄皮书第98页：偏迹是唯一可以正确描述复合子系统内可观测量的运算）

4.C1 VS C2

因为在进行全局去相，每个qubit之间去相结果之间是乘积关系；但是对于局部去相，每个去相结果之间是累加关系，所以当n过大，C1会出现梯度随n呈现指数级别消失，但是C2只是呈现多项式级别消失。

5.不同代价函数的训练效果

为什么不能直接利用C1或者C2训练参数，还要借助q，同时利用C1,C2构成一个新的代价函数呢？我们借助下面这个图像解决一下这个问题。

原文作者提出当量子比特数目n<6的时候，可以直接利用代价函数C1训练参数，但是通过图表，我们可以观察到当n>=6的时候，直接利用C1训练无法达到收敛，两种间接训练效果要比直接训练效果要好，是可以达到收敛效果的。

通过图中我们可以单纯利用C2是可以达到收敛效果的，C3（q=0.5,红色曲线）也是可以达到收敛的，但是我们不能单纯说此时训练效果C2>C3>C1，因为他们之间并没有一个统一的量，能进行比较的就是紫色曲线VS绿色曲线，黄色曲线VS绿色曲线，黄色曲线VS紫色曲线。

为什么红色曲线不能够和紫色曲线进行对比呢？？？我以为是可以的，但是师兄这边的解释是不可以的。说是比较标准不一样，因为选择的代价函数不同。对于这两条曲线，他们只是选择的参数是一样的，但是选择的代价函数并不相同，他们都能够达到收敛，只是迭代次数是不同的而已，不能单纯的凭借迭代次数多少就说哪一个好哪一个不好。

综上所述，我们对比的：紫色曲线VS绿色曲线，黄色曲线VS绿色曲线，黄色曲线VS紫色曲线，他们都是选择了同一个代价函数C1，只是参数不同而已。